Phy5645/Gamowfactor
Calculation of Gamow Factor for Alpha decay of Nuclei
Since the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} -decay happens in the nulcie then we can assume that an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} -decay is formed in the nucleus just before its emission (although Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} particle doesnot exist in the nucleus). Inside the nucleus the particle will experience nuclear interaction which mostly attractive and outside the nucleus the inetraction would be coulombic(replusive).
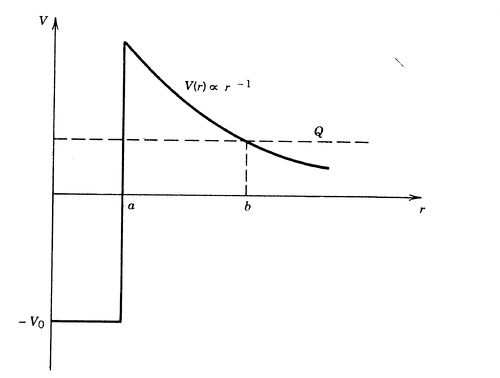
Since the mathematical form of the nuclear interaction is not known we can model it by a square well type potential for the present purpose. Outside the range of the nuclear interaction would be coulombic. So the coulomb interaction is,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{coul} = \frac{1}{4\pi\epsilon_{0}}\frac{2z_{1}e^{2}}{r}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{1}} is the atomic number of the rest of the nucleus(after decay).
From the WKB apporximation we know that at the turning point, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E= V(x)= V_{coul} = \frac{1}{4\pi\epsilon_{0}}\frac{2z_{1}e^{2}}{R_{c}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{c} = \frac{1}{4\pi\epsilon_{0}}\frac{2z_{1}e^{2}}{E}}
Now the Transition probabilty Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\cong \Theta ^{2}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Theta = e^{-\int_{b}^{a}q(x)dx}}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q(x)= \frac{1}{\hbar}\sqrt{2m\left(V(x)-E\right)}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Theta ^{2} = e^{-2\int_{b}^{a} q(x)dx}}
In the present problem Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b= R} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = R_{c}}
Now, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{R}^{R_{c}} \left(\frac{2m}{\hbar^{2}}\right)^{\frac{1}{2}}(V(x)-E)^{\frac{1}{2}} dr = \left(\frac{2m}{\hbar^{2}}\right)^{\frac{1}{2}}\int_{R}^{R_{c}} \left(\frac{1}{4\pi\epsilon_{0}}\frac{2z_{1}e^{2}}{r}-E\right)^\frac{1}{2}dr}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \left(\frac{2m}{\hbar^{2}}\right)^{\frac{1}{2}}\left(\frac{2z_{1}e^{2}}{4\pi\epsilon_{0}}\right)^{\frac{1}{2}}\int_{R}^{R_{c}} \left [ \frac{1}{r} - \frac{1}{R_{c}}\right ]^{\frac{1}{2}}dr}
let, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I = \int_{R}^{R_{c}} \left [ \frac{1}{r} - \frac{1}{R_{c}}\right ]^{\frac{1}{2}}dr}
Put,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r= R_{0}cos^{2}\theta}
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dr= -R_{0}2cos\theta sin\theta}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I= 2\int_{0}^{cos^{-1}\sqrt{\frac{R}{R_{c}}}} \left( \frac{R_{c}sin^{2}\theta}{cos^{2}\theta}\right)^{\frac{1}{2}} cos\theta sin\theta d\theta}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2R_{c}^{\frac{1}{2}}\int_{0}^{cos^{-1}\sqrt{\frac{R}{R_{c}}}} sin^{2}\theta d\theta }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I= R_{c}^{\frac{1}{2}}\int_{0}^{cos^{-1}\sqrt{\frac{R}{R_{c}}}} ( 1-{cos2\theta}) d\theta}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I= R_{c}^{\frac{1}{2}}\left [ \theta - sin\theta cos\theta \right ]_{0}^{cos^{-1}\sqrt{\frac{R}{R_{c}}}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I= R_{c}^{\frac{1}{2}}\left [ cos^{-1}\sqrt{\frac{R}{R_{c}}} - sin \left(cos^{-1}\sqrt{\frac{R}{R_{c}}}\right) cos\left(cos^{-1}\sqrt{\frac{R}{R_{c}}}\right) \right ]}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I= R_{c}^{\frac{1}{2}}\left [ cos^{-1}\sqrt{\frac{R}{R_{c}}} - \sqrt{\frac{R}{R_{c}}}\sqrt{1- \frac{R}{R_{c}}} \right ]}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I= R_{c}^{\frac{1}{2}}\left [ cos^{-1}\sqrt{\frac{R}{R_{c}}} - \sqrt{\frac{R}{R_{c}}- \left(\frac{R}{R_{c}}\right)^{2}} \right ]}
Let us consider Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{c} \gg R}
Then we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I\cong \sqrt{R_{c}}\left(cos^{-1}\sqrt{\frac{R}{R_{c}}}-\sqrt{\frac{R}{R_{c}}} \right)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cos^{-1}\sqrt{\frac{R}{R_{c}}} \cong \frac{\pi}{2} - \left(\frac{R}{R_{c}}\right)^{\frac{1}{2}}}
Setting, charge of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} particle = 2= Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{2}} (in general)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int q(x)dx = \left ( \frac{2Mz_{1}z_{2}e^{2}R_{c}}{\hbar^{2}4\pi\epsilon_0} \right )^{\frac{1}{2}}\left [\frac{\pi}{2} - 2\left(\frac{R}{R_{c}}\right)^{\frac{1}{2}} \right ]}
Now Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\cong e^{-2\int q(x)dx} = exp\left [ -\frac{\pi z_{1}z_{2}e^{2}}{\hbar 4\pi\epsilon_0} \left (\frac{2M}{e} \right )^{2} + \frac{4}{\hbar} \left ( \frac{2z_{1}z_{2}e^{2}MR}{4\pi\epsilon_0} \right )^{\frac{1}{2}}\right ]}
Now putting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E= \frac{1}{2}mv^{2}} , veloctiy of the particle
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\cong exp\left ( \frac{-2\pi z_{1}z_{2}e^{2}}{4\pi\epsilon_0\hbar v} \right )exp \left ( \frac{32z_{1}z_{2}e^{2}MR}{4\pi\epsilon_0\hbar^{2} } \right )^{\frac{1}{2}}}
The 1st exponential term is known as the Gamow factor. The Gamow factor determines the dependence of the probability on the speed (or energy) of the alpha particle.
Back to WKB in Spherical Coordinates