Solution to Set 7

Problem 1

Describe the classifications of solids according to the band theory. Pay particular attention to materials on the borderlines of different classifications. Specifically, discuss the electrical conduction at 0K and finite temperatures, and the type of charge carriers involved.

Description

In solid states, atoms have limited degrees of freedom. So instead of having discrete energies as in the case of free atoms, the available energy states of solids form bands. There are gaps between the conduction and valence bands.

• Fermi level is the top of the available electron energy levels at low temperatures.
• Conduction Band is energy at which the electrons can accelerate freely through the material. Under the influence of an applied electric field, they can produce an electric current
• Valence Band nests the valence electrons, which are electrons in the outermost shell of an atom. It requires increased tempearture and energy levels to free a valence electron.
• Energy Gap (aka "Band Gap") is an energy range in a solid where no electron states exist. For insulators and semiconductors, the band gap generally refers to the energy difference (in electron volts) between the top of the valence band and the bottom of the conduction band; it is the amount of energy required to free an outer shell electron from its orbit about the nucleus to a free state.
• The Classification of Solids
  • Insulators: Electrons in the valence band are separated by a large gap from the conduction band
  • Semiconductors: There is a small enough gap between the valence and conduction bands that thermal or other excitations can bridge the gap. With such a small gap, the presence of a small percentage of a doping material can increase conductivity dramatically.
  • Conductors: (i.e. metals) The valence band overlaps the conduction band. Electrons can contribute to conduction.

Electrical Conduction

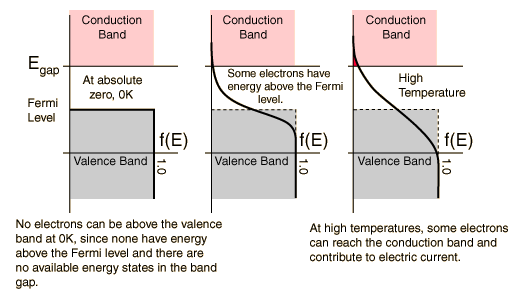
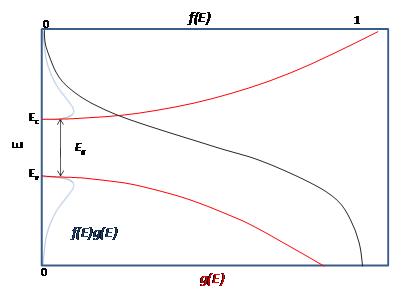
At finite temperatures, the number of electrons which reach the conduction band and contribute to current can be modeled by the Fermi function.

$f(E)={\frac {1}{e^{\tfrac {\Delta E}{kT}}+1}}$

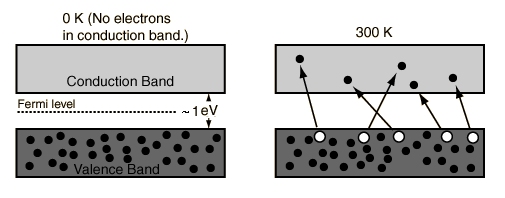
• At 0 Kelvin

No electrons can be above the valence band, since none have energy above the Fermi level and there are no available energy states above the band gap

• Between 0 Kelvin and High Temperatures

Some electrons have energy have energy above the Fermi level, but these electrons stay within the gap between the conduction band above and the valence band below.

• At High Temperatures

Some electrons can reach the conduction band and contribute to the electric current. However, this current is small compared to the current in doped semiconductors under the same conditions.

Charge Carriers

There are 2 types of charge carriers.

• Electrons carry negative charge
• Band gaps, the traveling vacancies in the valence-band electron population, carry positive charge.

Problem 2

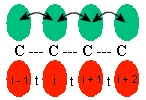
Consider a one-dimensional tight-binding model describing the dimerized state of polyacetylene (C₂H₂)_n, where the p-electron orbitals hopping elements $t_{1}\;$ and $t_{2}\;$ (with $t_{1}>t_{2}\;$) alternate along the chain.

Derivation of Band Structure for Polyacetylene

Derive the band structure for this model.

"Dimerized" means that the carbon are not equally spaced as you see in the lecture notes. They are "conjugated polymers". For now, disregard the hydrogen, they are merely hanging out by the sidelines. Consider the carbons as a localized carbon chain.

• Given
  • $a'=2a\;$
  • $t(a)~e^{-{\tfrac {a}{a_{0}}}}\;$

• Result

$E_{k}=\pm ((t_{1}^{2}+t_{2}^{2}+2t_{1}t_{2}\cos {(ka')})^{\frac {1}{2}}\!$

Substituting $k={\frac {\pi }{a'}}$, we get

$E_{gap}=\pm (t_{1}^{2}+t_{2}^{2}-2t_{1}t_{2})^{\frac {1}{2}}=(t_{1}-t_{2})\!$

Discuss what happens in the limit when $t_{1}\rightarrow t_{2}$

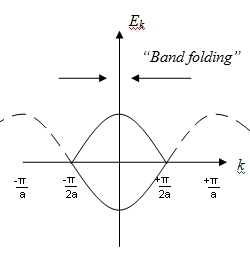
The phenomena of Band Folding happens.

$\lim _{t_{1}\to t_{2}}E_{gap}=t_{2}-t_{2}\Rightarrow 0$

Comparison between Polyacetylene Chain and Simple Chain

Compare this result with that obtained for a simple chain (discussed in class) where $t_{1}=t_{2}=t\;$.

$E_{C_{2}H_{2}}=t_{1}-t_{2}=t_{2}-t_{2}=0\;$

$E_{simple}=-t=-t_{2}=-t_{1}\;$

$E_{C_{2}H_{2}}>E_{simple}\;$

Band Folding

Explain the phenomenon of band-folding.

Not shown here, but the y-axis reads +2t and -2t.

Density of States

Sketch the density of states for this model.

Problem 3

In the Feynman model of energy bands, the energy dispersion of electrons in a cubic lattice is given by

$E(k)=E_{o}-2Acos(|\mathbf {k} |a)$,

where $a\;$ is the lattice constant.

(a) Effective Mass

Derive an expression for the effective mass for this band.

$Fdt=dp=\hbar dk\;$ where p = momentum

$F=m_{e}{\frac {dv}{dt}}==-qE=-eE\;$

$F=\hbar {\frac {dk}{dt}}\;$

${\frac {dv}{dt}}={\frac {1}{\hbar }}{\frac {d}{dt}}\left({\frac {dE}{dk}}\right)={\frac {1}{\hbar }}{\frac {d}{dk}}\left({\frac {dk}{dt}}{\frac {dE}{dk}}\right)\;$

$F=\left({\frac {\hbar }{\tfrac {d^{2}E}{dk}}}\right){\frac {dv}{dt}}\;$

$m_{e}=\hbar ^{2}/{\tfrac {d^{2}E}{dk^{2}}}\;$

(b) Effective Mass and Band Width

Prove that the effective mass at the bottom of the band is inversely proportional to the band width.

$m_{e}=\hbar ^{2}/{\tfrac {d^{2}E}{dk^{2}}}\;$

$m_{e}{\tfrac {d^{2}E}{dk^{2}}}=\hbar ^{2}\;$

$m_{e}d^{2}E=\hbar ^{2}dk^{2}\;$

$\int m_{e}d^{2}E=\int \hbar ^{2}dk^{2}\;$

$m_{e}dE=\hbar ^{2}dk\;$

$m_{e}dE=\hbar ^{2}kdk\;$

$dE={\frac {\hbar ^{2}k}{m_{b}}}dk_{min}=0\;$

$E={\frac {\hbar ^{2}k_{min}^{2}}{2m_{b}}}\;$

(c) Electronic Density of State

Derive an expression for the electronic DOS in this band.

Volume in 3D

$V\cdot dk=4\pi |k|^{2}dk$

The number of states is given simply by dividing this volume by the volume of a single energy state. At this point is convenient to introduce an additional factor of two to account for the intrinsic angular momentum of the electrons or spin states. The result is:

$g(k)dk=2{\frac {V\cdot dk}{V}}={\frac {|k|^{2}\cdot dk\cdot L^{3}}{\pi ^{2}}}$

$E={\frac {\hbar ^{2}k^{2}}{2m}}\;$

$|k|={\sqrt {\frac {2mE}{\hbar ^{2}}}}\;$

$dk={\frac {1}{\sqrt {\tfrac {2mE}{\hbar ^{2}}}}}{\frac {m}{\hbar ^{2}}}dE\;$

$g(E)dE={\frac {k^{2}\cdot dk}{\pi ^{2}}}\;$ $={\frac {2mE}{\pi ^{2}\hbar ^{2}}}\left({\frac {2mE}{\hbar ^{2}}}\right)^{1/2}{\frac {m}{\hbar ^{2}}}dE\;$ $={\frac {1}{2\pi ^{2}}}\left({\frac {2m}{\hbar ^{2}}}\right)^{3/2}E^{1/2}dE\;$

(d) DOS and Free Electron Energy Dependence

Prove that at the bottom of the band the DOS has the same energy dependence as that for free electrons.

$E_{b}=E_{f}\;$

${\frac {\hbar ^{2}k_{min}^{2}}{2m_{b}}}={\frac {\hbar ^{2}k^{2}}{2m}}\;$

Problem 4

Our understanding of the electrical conductivity of metals evolved from the classical free electron gas to quantum free electron gas to the band theory. Write a short essay describing this evolution. Specify the new physics introduced in each model.

Definition

Metals have overlapping conduction bands and valence bands in their electronic structure. The theory of conductivity came from the fact that one or more valence electrons can become relatively free to travel throughout the solid material. This connection is formalized in the Wiedemann-Franz law. The quantum properties of metals are often stated in terms of their Fermi energy and their free electron density.

Classical Free Electron Model

An early model of electrical conduction was the Drude model, which applied kinetic theory to the electrons in a solid. By assuming that the material contains immobile positive ions and an "electron gas" of classical, non-interacting electrons, the Drude model was able to explain electrical and thermal conductivity and the Hall effect in metals, although it greatly overestimated the electronic heat capacity.

Quantum Free Electron Model

Arnold Sommerfeld combined the classical Drude model with quantum mechanics in the free electron model (or Drude-Sommerfeld model). Here, the electrons are modelled as a Fermi gas, a gas of particles which obey the quantum mechanical Fermi-Dirac statistics. The free electron model gave improved predictions for the heat capacity of metals, however, it was unable to explain the existence of insulators.

Band Theory (aka the Nearly-Free Electron Model)

The band theory explains the existence of conductors, semiconductors and insulators. It introduces a weak periodic perturbation, meant to model the interaction between the conduction electrons and the ions in a crystalline solid. This is also called the Nearly-Free Electron Model.

The nearly-free electron model rewrites the Schrödinger equation for the case of a periodic potential. The solutions in this case are known as Bloch states. Since Bloch's theorem applies only to periodic potentials, and since unceasing random movements of atoms in a crystal disrupt periodicity, this use of Bloch's theorem is only an approximation, but it has proven to be a tremendously valuable approximation, without which most solid-state physics analysis would be intractable. Deviations from periodicity are treated by quantum mechanical perturbation theory.