Phy5670/QLG

Introduction

A lattice model first proposed in 1956 has been introduced to explain the peculiar properties and phase transitions in liquid helium.In this model, the liquid is regarded as a lattice composed of atoms and holes, where each atom can migrate by exchanging its position with an adjacent hole.The kinetic and potential energies are defined in terms of creation and annihilation operators for the atom sin each lattice site such that they boil down to the appropriate form in the limit of vanishing lattice spacing.An analogy has been drawn between the lattice liquid and a system of vector spins subjected to an external magnetic field, with identification of corresponding physical quantities.Finally,the quantum lattice gas model has been implemented to describe essential aspects of the motion of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{4}\textrm{He}} atoms and of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{3}\textrm{He}} impurities in solid Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{4}\textrm{He}} .The study suggested the affinity of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{3}\textrm{He}} impurities to bind to defects and promote Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{4}\textrm{He}} atoms to interstitial sites which can turn the bosonic quantum disordered crystal into a metastable supersolid.It is further proposed that such defects can form a glass phase during the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{4}\textrm{He}} solid growth by rapid cooling.

Lattice Gas Model of Liquid Helium

The Lattice Gas Model

The lattice model for classical liquid is well known for providing an adequate approximation for the purpose of taking into consideration the large atomic correlation in liquid phase.Each atom is assumed to occupy only discrete lattice points and the configurations of liquid are described by the distributions of atoms and holes among the lattice points.By choosing a proper magnitude of lattice constant, and excluding the multiple occupation of atoms on each lattice point, one can account for the effect of the strong repulsion between atoms. In extending this idea of lattice model to quantum liquid such as liquid helium, it is of importance to take into account of the effect of the zero point motion of the atoms.Since, considerable increment in kinetic energy will be caused by localizing each atom in the lattice configuration, it must be reduced by mixing various configurations.Thus, in the lattice representation on which our lattice model rests, the kinetic energy has large non-diagonal elements such as to produce transitions among various lattice configurations.Taking consideration of this effect of the kinetic energy on one hand, and of the excluding effect of the strong repulsion between atoms on the other hand, we shall construct a lattice model for liquid helium. For simplicity, we assume a simple cubic lattice of lattice constant d. Adopting the scheme of second quantization, we define operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathit{a_{i}^{\ast }}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathit{a_{i}^{}}} which creates and annihilates an atom at the i-th lattice point. We assume the commutation relations,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\mathit{a_{i}^{\ast }},\mathit{a_{j}^{\ast }}]_{-} = [\mathit{a_{i}},\mathit{a_{j}}]_{-} = [\mathit{a_{i}},\mathit{a_{j}^{\ast }}]_{-} = 0 \;\; for\;\; i\neq j}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\mathit{a_{i}^{\ast }},\mathit{a_{i}^{\ast }}]_{+} = [\mathit{a_{i}},\mathit{a_{i}}]_{+} = 0, [\mathit{a_{i}},\mathit{a_{i}^{\ast }}]_{+} = 1 \;\; for\;\; i= j} In other words, the operators with different lattice indices are commutable to each other and with respect to the same lattice point they Fermionic character. Now, we set up the potential energy of the lattice liquid.We consider the potential energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathit{v}} betwwen two atoms so that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathit{v}=\infty} for two atoms in same lattice points.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathit{v}=-\mathit{v_{o}}} otherwise.

Then, the total potential energy of the system Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi =-\mathit{v_{o}}\sum_{<ij>}\mathit{a_{i}^{\ast }}\mathit{a_{i}}\mathit{a_{j}^{\ast }}\mathit{a_{j}}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <ij>} means summation over nearest neighbouring pair points. As to the kinetic energy, we assume that each atom can make transition only to one of the nearest neighbour sites when it is vacant.So, the proposed kinetic energy of the system Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K=(\frac{\hbar^{2}}{2md^{2}})\sum_{<ij>}(\mathit{a_{i}^{\ast }}-\mathit{a_{j}^{\ast }})(\mathit{a_{i}}-\mathit{a_{j}})} The total number of atoms is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i}\mathit{a_{i}^{\ast }}\mathit{a_{i}}=N_{0}} Making Fourier transforms of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathit{a_{i}^{\ast }}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathit{a_{i}}} as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathit{a_{\mathbf{k}}^{\ast }}=N^{-\frac{1}{2}}\sum_{j}e^{(-i\mathbf{kr}_{j})}\mathit{a_{j}^{\ast }}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathit{a_{\mathbf{k}}}=N^{-\frac{1}{2}}\sum_{j}e^{(i\mathbf{kr}_{j})}\mathit{a_{j}}}

Then, the kinetic energy can be written in the form

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K\cong \sum_{\mathbf{k}}(\frac{\hbar^{2}\mathbf{k^{2}}}{2m})\mathit{a_{\mathbf{k}}^{\ast }}\mathit{a_{\mathbf{k}}}} provided Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle kd\ll 1} . Putting together both the kinetic energy and potential energy terms, the total Hamiltonian for the lattice liquid

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{L}=(\frac{\hbar^{2}}{2md^{2}})\sum_{<ij>}(\mathit{a_{i}^{\ast }}-\mathit{a_{j}^{\ast }})(\mathit{a_{i}}-\mathit{a_{j}})-\mathit{v_{o}}\sum_{<ij>}\mathit{a_{i}^{\ast }}\mathit{a_{i}}\mathit{a_{j}^{\ast }}\mathit{a_{j}}}

Information about the thermodynamic properties of our lattice liquid can be obtained by constructing the Grand canonical partition function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Xi_{L}=Tr[e^{(-\alpha\sum_{i}\mathit{a_{i}^{\ast }}\mathit{a_{i}}-\beta H_{L})}]}

Thus, defining the characteristic function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{\psi }= log\; \Xi _{L}} ,

the number of atoms Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{0}=-(\frac{\partial\bar{\psi } }{\partial \alpha })_{\beta }}

internal energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = -(\frac{\partial\bar{\psi } }{\partial \beta })_{\alpha }}

pressure Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle pV/kT = \bar{\psi }} and so on.

Spin System eqivalent to the lattice model

Now we consider a set of N spins each of which is localized at each lattice point and has a magnitude of 1/2. Then, the spin operators, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{j\pm }= S_{jx}\pm iS_{jy}} satisfy similar commutation relations:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [S_{i+},S_{j+}]_{-}= [S_{i-},S_{j-}]_{-}=[S_{i-},S_{j+}]_{-}=0\; \; (i\neq j)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [S_{i+},S_{i+}]_{+}= [S_{i-},S_{i-}]_{+}=0,\; \; [S_{i-},S_{i+}]_{+}=1\; \; (i=j)}

Besides, the z component of spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{iz}} can be expressed as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{iz}=S_{i+}S_{i-}-\frac{1}{2}} .So, there should exist a system of spins equivalent to the lattice liquid with the lattice Hamiltonian by the correspondence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathit{a_{i}^{\ast }}\leftrightarrow S_{i+}, \mathit{a_{i}}\leftrightarrow S_{i-}} .

We consider the spin system whose Hamiltonian is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{F}=-J\sum_{<ij>}{(S_{ix}S_{jx}+S_{iy}S_{jy})}-J^{'}\sum_{<ij>}{S_{iz}S_{jz}}-H\sum_{i}{S_{iz}}}

Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{F}} represents the energy of spin which interact with an anisotropic exchange coupling and are subjected to an external magnetic field. Using the commutation relations, the Hamiltonian can easily be written as: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{F}=\frac{J}{2}\sum_{<ij>}(S_{i+}-S_{j+})(S_{i-}-S_{j-})-J^{'}\sum_{<ij>}S_{i+}S_{i-}S_{j+}S_{j-}-(H+\frac{z}{2}J-\frac{z}{2}J^{'}){\sum_{i}S_{i+}S_{i-}}+\frac{N}{2}(H-\frac{1}{4}zJ^{'})} where z is the number of nearest neighbours.Now the partition function of this spin system is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Xi _{F}=Tr[e^{(-\beta H_{F})}]}

Then comparing with our lattice gas model, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Xi _{L}=C\Xi _{F}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar^{2}}{2md^{2}}=\frac{J}{2}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathit{v_{o}}=J^{'}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha =-\beta[ {H+(\frac{z}{2})J-(\frac{z}{2})J^{'}}]\; ,\; C=e^{[(\frac{N}{2})\beta [H-(\frac{z}{4})J^{'}]]}}

Therefore, if we know the thermodynamic properties of our spin system, we can presume the behaviours of our lattice liquid by simple translation, and vice versa.

The relation between the physical quantities of both systems can be found straightforwardly. The density of the lattice liquid is connected with the magnitude of the magnetization of the spin systemalong z axis.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{0}=-\frac{\partial (log \Xi _{L})}{\partial \alpha }}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{\partial(logC+log\Xi _{F})}{\partial (\beta H)}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{N}{2}+<\sum S_{iz}>}

Denoting the density of lattice liquid by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{N_{0}}{N}=\rho } and the mean value of the z component of spin by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <S_{z}>=\zeta } , then it holds that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\rho =1+2\zeta } It is natural to assume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\rho =1+2\zeta } for liquid phase and so we may confine ourselves to the case $\zeta >0$.The chemical potential of the lattice liquid $\mu =-{\frac {\alpha }{\beta }}$ corresponds to the external magnetic field apart from an adiditive constant.The pressure of the lattice liquid is identified with a linear combination of free energy per one spin f and external magnetic field:

$pd^{3}=-f+{\frac {1}{2}}(H-{\frac {z}{4}}J^{'})$

where $f=-({\frac {1}{\beta N}})log\Xi _{F}$ and the volume $V=Nd^{3}$

The kinetic energy of the lattice liquid corresponds to the exchange energy of spins which prefer to direct perpendicularly to the z axis, if externel magnetic field is absent, on account of anisotropic exchange coupling.In other words, to maximize the negative of exchange energy by making as many spins as possible point in one direction in the xy plane corresponds to minimize the kinetic energy of the lattice liquid by making the localization of each atom as small as possible. And when the spin system magnetizes spontaneously at sufficiently low temperatures, there appears a long range order by which the direction of any two spins, however distant, are correlated to each other.Corresponding to this phenomena of long range order in ferromagnets, there would appear in the lattice liquid a kind of 'long range order of momentum', which might be responsible for superfluidity in helium.

Phase Transition in Helium

In the preceding section, we found that there exists an intimate connection between the thermodynamical properties of the system of ferromagnets and that of the lattice liquid. Therefore, one can expect that the appearance of ferromagnetic ordering in one system will be related to the occurrence of the $\lambda -transition$ or of superfluidity in the other. In order to examine thus relation, it is more convenient to start with the ferromagnetic system because the physical phenomenon involved in this system are more familiar and more easily understood by institution. First we shall classify two cases according as ${J}'>J$ or $J>{J}'$

The case of ${J}'>J$

This os the case where the exchange coupling in the z-direction is stronger than that in the x or y direction, and hence at sufficiently low temperatures a spontaneous magnetization appears along the z-axis. This implies in the lattice liquid there appears an order of distribution of atoms and holes such that atoms and holes congregate separately to each other. This case should rather be regarded as the case where solid-liquid or liquid-gas condensation occurs. To exclude such a phase separation, we must impose a condition

$J\geq {J}'$

or ${\mathit {\hbar /md^{2}}}\geq vo$

Now, above equation can be considered as a condition that the lattice system is a homogeneous "quantum liquid" down to absolute zero.

The case of $J>{J}'$

In this case a spin ordering in the xy plane will exhibit at sufficiently low temperature. To see what happens in the lattice liquid, we shall first solve the problem of the ferromagnetism by means of molecular field approximation, and then translate the results into the language of the lattice liquid.

Replacing the exchange interaction between the neighboring states spins by molecular field, the one spin Hamiltonian is written as

$H_{1}=-zJ\xi S_{x}-(H+z{J}'\zeta )S_{z}=-aS_{x}-bS_{z}$

where

$a=zJ\xi ,b=H+z{J}'\zeta$

and $\xi$ and $\zeta$ are statistical averages of $S_{x}andS_{z}$ respectively, defined by

$\xi ={\frac {\partial }{\partial (\beta a)}}log[Trace(exp(-\beta H_{1}))]$

$\zeta ={\frac {\partial }{\partial (\beta b)}}log[Trace(exp(-\beta H_{1}))]$

The eigenvalues of the Hamitonian can be obtained as $\pm (1/2){\sqrt {a^{2}+b^{2}}}$, and by noting that

$Trace[exp(-\beta H_{1})]=2cosh{\frac {\beta }{2}}{\sqrt {a^{2}+b^{2}}}$

and $\xi ={\frac {a}{2{\sqrt {a^{2}+b^{2}}}}}tanh{\frac {\beta }{2}}{\sqrt {a^{2}+b^{2}}}$

$\zeta ={\frac {b}{2{\sqrt {a^{2}+b^{2}}}}}tanh{\frac {\beta }{2}}{\sqrt {a^{2}+b^{2}}}$

Now there appear two cases:

(i) a=0, i.e. $\xi =0$

This is trivial solution. In this case the spontaneous magnetization is absent and magnetization along the z-axis is given by

$\zeta ={\frac {1}{2}}tanh{\frac {\beta }{2}}b$

or

$2\zeta =tanh\left({\frac {H+z{J}'\zeta }{2kT}}\right)$ As is proved shortly, this state is stable over all the range of temperature when H exceeds a critical field $H_{0}$ and is stable only above a critical temperature $T_{0}$ when $H<H_{0}$

(ii) $a\neq 0$

From above equations it follows that

${\frac {2}{zJ}}{\sqrt {a^{2}+b^{2}}}=tanh{\frac {\beta }{2}}{\sqrt {a^{2}+b^{2}}}$

or putting $X={\frac {2}{zJ}}{\sqrt {a^{2}+b^{2}}}$, $T_{o}={\frac {zJ}{ak}}$

$X=tanh(T_{o}/T)X$

The above equation has a non-zero solution $0\leq X(T)\leq 1$ when $T<T_{0}$, in addition to a trivial solution X=0. On the other hand, combining equations above mentioned we get,

$\zeta ={\frac {b}{zJ}}=(H+z{J}'\zeta )/zJ$

and thence

$\zeta =H/z(J-{J}')$

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi^{2}+\zeta^{2}=(1/4)X^{2}(T)}

When H is given, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta} is a constant (independent of temperature) and has to satisfy an inequality

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta\leq (1/2)X(T)} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2H/z(J-{J}')\leq X(T)\leq 1}

from which critical field is determined:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}=(z/2)(J-{J}')}

For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H>H_{0}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} cannot be finite and we should go back to the case (i) where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I\xi=0} . For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H<H_(0)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle zeta} is a constant given by above equations, whereas Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta} decreases with increasing temperatures and lastly vanishes at the critical temperatureFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{0}} determined by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\zeta=2H/z(j-{J}')=X(T_{c})}

Above the critical temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T>T_{c}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta} remains vanishing and again we have the case (i). We summarize these results in figures given below, in which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle /zeta} is plotted as a function of T (under constant field H) or of H (under constant T). The physical meaning of these results will be quite obvious.

We are dealing with an assembly of spins, each of which is subjected to two competitive forces. One is the external magnetic field whichturns the spins to the z-direction and the other is the exchange force which acts so as to put the spins into order in the plane perpendicular to the z-axis. When the external field overwhelms the exchange force, the ferromagnetic ordering is impossible, whereas a cooperative ordering of spins is established when the exchange force surpasses the decoupling effect of the external field and the thermal agitation. Once the ferromagnetic ordering in the xy-plane is set up, it becomes difficult to magnetize the spin system along the direction of the field.

Now let us see what kind of phase change occurs in the lattice liquid. As the density of the lattice liquid is related to the magnetization along the z-axis and the chemical potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} to the magnetic field H, the variation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} with temperature will be known by seeking for the cross points of the constant field curves as shown in figure with a horizontal line corresponding to a given density. The results are shown in figure given below, from which one can draw the following conclusions:

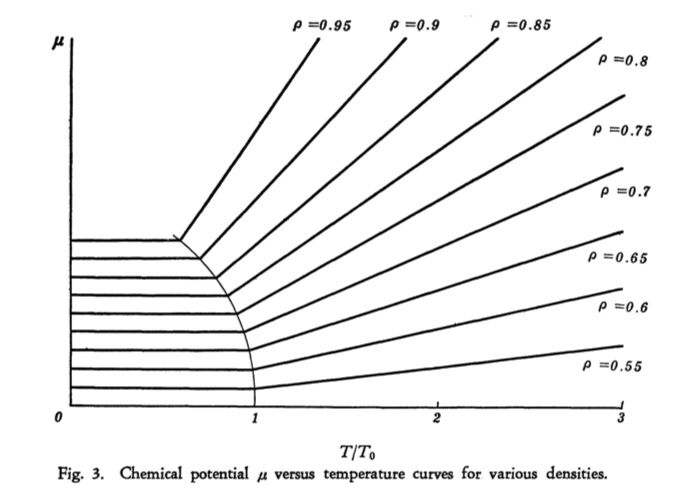
(1) A phase transition occurs at a critical temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{c}} .

This is of the second kind, because the chemical potential reveals a kink at this point. Now clearly, the density dependence of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{c}} is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2\rho -1)=tanh(T_{o}/T_{c})(2\rho -1)}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{o}=sJ/4k=z\hbar^{2}/4md^{2}k}

If we identify this transition with the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} -transition of liquid helium, the above equation yields a fairly excellent agreement between calculated and observed transition temperatures. For instance, if we take m as the true mass of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle He_{4}} (i.e. m=6.68 X $10_{-24}$gr.) and choose a lattice constant d= 3 X $10_{-8}$cm with z=6, then $T_{0}=2^{0}$K

For several values of mass density $\rho _{M}=m/d^{2}\rho$, the calculated $T_{\lambda }$ values are tabulated in table given below together with the observed values.

All other thermodynamical quantities can be easily evaluated, if the free energy of the spin system is known. The free energy per one spin is in the present approximation evaluated as

$f={\frac {z}{2}}J\xi ^{2}+{\frac {z}{2}}{J}'\zeta ^{2}-kTlog[2cosh{\frac {2T_{0}}{T}}{\frac {\sqrt {\zeta +(H+z{J}'\zeta )^{2}}}{(zJ)^{2}}}]$

The condition ${\frac {\partial f}{\partial \xi }}=0$ and ${\frac {\partial f}{\partial \zeta }}=0$ give the previously mentioned equation. One cannot, however, expect a quantitative agreement between theory and experiment because of the neglect of he short range order.

Possible Role of $^{3}{\textrm {He}}$ impurities in solid $^{4}{\textrm {He}}$

The Hamiltonian

In this section, we discuss the role of very low density of impurities in a bosonic hard core solid.Our model that describes the impurity motion in an otherwise ideal quantum bosonic crystal, maps to a quantum spin model with antiferromagnetic coupling and antiferromagnetic order in one direction and ferromagnetic coupling in the perpendicular direction with impurities moving through the lattice.The impurity motion between sub-lattices couples to quantum fluctuations of these pseudo-spin degreesof freedom which correspond to the boson hopping from an occupied site of the solid to an empty interstitial site.We find that for the limit which describes the case of solid $^{4}{\textrm {He}}$, interstitial atoms are well-defined delocalized excitations. Let us consider a lattice gas model to describe the bosonic solid and the added impurities.In such a model,we need to consider the interstitial sites as part of the lattice and, thus, the ideal quantum solid containing no vacancies and no impurities, corresponds to a fractionally occupied lattice.For example, the ideal triangular solid corresponds to the case of 1/3 filling, namely to a ${\sqrt {3}}\times {\sqrt {3}}$ ordered solid and the ideal square lattice solid corresponds to the ${\sqrt {2}}\times {\sqrt {2}}$ checkerboard solid, i.e., 1/2 filling of the lattice with bosons. Our model Hamiltonian describing a bosonic quantum solid (such as solid $^{4}{\textrm {He}}$ ) and a small concentration of impurities (such as $^{3}{\textrm {He}}$ atoms) may be written as follows:

${\hat {H}}={\hat {H}}_{B}+{\hat {H}}^{\ast }+{\hat {H}}_{int}-\mu \sum _{i}{\hat {N}}_{i}-\mu ^{\ast }\sum _{i}{\hat {n}}_{i}$

${\hat {H}}_{B}=\sum _{<ij>}[-t_{b}(B_{i}^{\dagger }B_{j}+h.c.)+V{\hat {N_{i}}}{\hat {N}}_{j}]+U\sum _{i}{\hat {N_{i}^{2}}}$

${\hat {H}}^{\ast }=\sum _{<ij>}[-t(c_{i}^{\dagger }c_{j}+h.c.)+W{\hat {n_{i}}}{\hat {n}}_{j}]+U^{\ast }\sum _{i}{\hat {n_{i}^{2}}}$

${\hat {H}}_{int}=V^{\ast }\sum _{<ij>}({\hat {N}}_{i}{\hat {n_{j}}}+{\hat {n}}_{i}{\hat {N}}_{j})+U^{'}\sum _{i}{\hat {n_{i}}}{\hat {N_{i}}}$

$H_{B}$ is the Hamiltonian of the bosonic solid, and $B_{i}^{\dagger }(B_{i})$ are the boson creation (annihilation) operators and ${\hat {N_{i}}}=B_{i}^{\dagger }B_{i}$.The fermion operators $c_{i}^{\dagger }(c_{i})$ create ( or annihilate ) impurities on the site i and we have suppressed their spin degree for simplicity.Here, $n_{i}$ is the impurity number operator.We will consider the $U\rightarrow \infty$,$U^{\ast }\rightarrow \infty$ and $U^{'}\rightarrow \infty$ limits (single-site occupation subspace) because of the hard-core interaction. $V,V^{\ast }\;$ and $\;W$ are positive because of the additional energy cost to place an atom in an interstitial site.

In the absence of impurities the well-known pure bosonic Hamiltonian in the limit of $U\rightarrow \infty$ and under the transformation $B_{i}^{\dagger }\rightarrow S_{i}^{+},B_{i}\rightarrow S_{i}^{-},N_{i}\rightarrow S_{i}^{z}-{\frac {1}{2}}$ where $({\hat {S_{i}^{x}}},{\hat {S_{i}^{y}}},{\hat {S_{i}^{z}}})$ are spin 1/2 operators, reduces to the anisotropic spin 1/2 Heisenberg model in the presence of external magnetic field:

${\hat {H}}_{B}=\sum _{<ij>}[JS_{i}^{z}S_{j}^{z}+J_{xy}(S_{i}^{x}S_{j}^{x}+S_{i}^{y}S_{j}^{y})]-H\sum _{i}S_{i}^{z}$

where J=V>0 and $J_{xy}=-2t_{b}<0$ and $H=\mu -{\frac {z}{2V}}$,z is the coordination number.

In order to illustrate the effects of the impurities on the stability of the quantum solid and, vice versa, we first consider the square lattice because of its simplicity.Following the general spin-wave (SW) theory for an ordered square lattice quantum antiferromagnet , we seperate the ordered square lattice in two sublattices, A (or up, or occupied) and B (down, or empty) and we consider boson operators $a_{i}^{\dagger }$ and $b_{i}^{\dagger }$ which create spin-deviations with respect to the classical Neel ground state in sites of the corresponding sublattice.The Hamiltonian is approximated by keeping terms up to quadratic in spin-deviation operators; using the Fourier transforms $a_{k}$ and $b_{k}$ of the operators $a_{i}$ and $b_{i}$, where k takes values fromthe Brillouin zone of the ${\sqrt {2}}\times {\sqrt {2}}$ sub-lattice and introducing the Bogoliubov canoonical transformation,

$a_{\mathbf {k} }=u_{k}\alpha _{\mathbf {k} }+v_{k}\beta _{\mathbf {-k} }^{\dagger }$

$b_{\mathbf {k} }=u_{k}\beta _{\mathbf {k} }-v_{k}\alpha _{\mathbf {-k} }^{\dagger }$

where $\alpha _{\mathbf {k} }^{\dagger }$ and $\beta _{\mathbf {k} }^{\dagger }$ are boson creation operators, the Hamiltonian takes the form

$H_{L}^{B}=E_{0}+\sum _{\mathbf {k} }(\omega _{\mathbf {k} }^{\alpha }\alpha _{\mathbf {k} }^{\dagger }\alpha _{\mathbf {k} }+\omega _{\mathbf {k} }^{\beta }\beta _{\mathbf {k} }^{\dagger }\beta _{\mathbf {k} })$

where $\omega _{\mathbf {k} }^{\alpha ,\beta }=dJ\epsilon _{\mathbf {k} }\pm H$

$\epsilon _{\mathbf {k} }={\sqrt {1-\lambda ^{2}\gamma _{\mathbf {k} }^{2}}}$

$\gamma _{\mathbf {k} }={\frac {1}{2}}(cos(k_{x})+cos(k_{y})),d=2,\lambda =J_{xy}/J$

$u_{\mathbf {k} }={\sqrt {{\frac {1}{2}}({\frac {1}{\epsilon _{\mathbf {k} }}}+1)}},v_{\mathbf {k} }=-sgn(\gamma _{\mathbf {k} }){\sqrt {{\frac {1}{2}}({\frac {1}{\epsilon _{\mathbf {k} }}}-1)}}$

It follows from the form of $H_{L}^{B}$ that for $\omega _{0}^{\alpha ,\beta }\geq 0$, i.e., for $H\geq dJ{\sqrt {1-\lambda ^{2}}}$, the Neel ordered ground state is unstable.Ferromagnetic order(superfluid in the Bose system) develops in the xy direction and the spins are canted in order to acquire a component along the direction of the field.The phase diagram obtained for this model with this spin-wave approximation agrees reasonably well with that obtained by other techniques.When the square lattice is half-filled there is a gap $G=dJ{\sqrt {1-\lambda ^{2}}}$for creating a propagating pseudo-spin wave excitation, i.e. to promote a boson atom to the interstitial band.These interstitial quasiparticles move in a band which in the limit of $J_{xy}\ll J$ has a bandwidth $W={\frac {dJ_{xy}^{2}}{2J}}$.

Bogoliubov transformation

Single bosonic case

Consider the canonical commutation relation for bosonic creation and annihilation operators in the harmonic basis

$\left[{\hat {a}},{\hat {a}}^{\dagger }\right]=1$

Define a new pair of operators

${\hat {b}}=u{\hat {a}}+v{\hat {a}}^{\dagger }$

${\hat {b}}^{\dagger }=u^{*}{\hat {a}}^{\dagger }+v^{*}{\hat {a}}$

where the latter is the hermitian conjugate of the first. The Bogoliubov transformation is a canonical transformation of these operators. To find the conditions on the constants u and v such that the transformation remains canonical, the commutator is expanded, viz.

$\left[{\hat {b}},{\hat {b}}^{\dagger }\right]=\left[u{\hat {a}}+v{\hat {a}}^{\dagger },u^{*}{\hat {a}}^{\dagger }+v^{*}{\hat {a}}\right]=\cdots =\left(|u|^{2}-|v|^{2}\right)\left[{\hat {a}},{\hat {a}}^{\dagger }\right].$

It can be seen that $|u|^{2}-|v|^{2}=1$ is the condition for which the transformation is canonical. Since the form of this condition is reminiscent of the hyperbolic identity $\cosh ^{2}x-\sinh ^{2}x=1$, the constants u and v can be parametrized as

$u=e^{i\theta _{1}}\cosh r\,\!$

$v=e^{i\theta _{2}}\sinh r\,\!.$

Fermionic case

For the anticommutation relation

$\left\{{\hat {a}},{\hat {a}}^{\dagger }\right\}=1$,

the same transformation with u and v becomes

$\left\{{\hat {b}},{\hat {b}}^{\dagger }\right\}=(|u|^{2}+|v|^{2})\left\{{\hat {a}},{\hat {a}}^{\dagger }\right\}$

To make the transformation canonical, u and v can be parameterized as

$u=e^{i\theta _{1}}\cos r\,\!$

$v=e^{i\theta _{2}}\sin r\,\!.$

General form of the transformation

The Hilbert space under consideration is equipped with these operators, and henceforth describes a higher-dimensional quantum harmonic oscillator (usually an infinite-dimensional one).

The ground state of the corresponding Hamiltonian is annihilated by all the annihilation operators:

$\forall i\qquad a_{i}|0\rangle =0$

All excited states are obtained as linear combinations of the ground state excited by some creation operators:

$\prod _{k=1}^{n}a_{i_{k}}^{\dagger }|0\rangle$

One may redefine the creation and the annihilation operators by a linear redefinition:

$a'_{i}=\sum _{j}(u_{ij}a_{j}+v_{ij}a_{j}^{\dagger })$

where the coefficients $u_{ij},v_{ij}$ must satisfy certain rules to guarantee that the annihilation operators and the creation operators $a_{i}^{\prime \dagger }$, defined by the Hermitian conjugate equation, have the same commutators.

The equation above defines the Bogoliubov transformation of the operators.

The ground state annihilated by all $a'_{i}$ is different from the original ground state $|0\rangle$ and they can be viewed as the Bogoliubov transformations of one another using the operator-state correspondence. They can also be defined as squeezed coherent states.

Motion of single impurity inside quantum solid

We wish to extend the approach introduced before to study the motion of a single impurity inside the quantum solid.We consider as reference state the Neel state with an impurity on the A (substitutional ) or B (interstitial) sublattices. We imagine that there exists operators $h_{i}^{\dagger }$ and $f_{i}^{\dagger }$ which operate on the Neel state and replace respectively an up-spin and down-spin with an impurity.For the single impurity case and by keeping only up to linear terms in spin-deviation operators, we can write:

${\hat {H}}^{\ast }+{\hat {H}}_{int}=-t\sum _{<ij>_{A}}(a_{i}^{\dagger }f_{j}^{\dagger }h_{i}+h.c.)+V^{\ast }d\sum _{i_{B}}f_{i}^{\dagger }f_{i}$

The entire linearized Hamiltonian, using the Bogoliubov transformation, takes the following form:

$H_{L}=\sum _{\mathbf {k} }[\epsilon _{1}h_{\mathbf {k} }^{\dagger }h_{\mathbf {k} }+\epsilon _{2}f_{\mathbf {k} }^{\dagger }f_{\mathbf {k} }]+\sum _{\mathbf {k,q} }[g_{\mathbf {kq} }^{(1)}(f_{\mathbf {k-q} }^{\dagger }h_{\mathbf {k} }\alpha _{\mathbf {q} }^{\dagger }+h_{\mathbf {k} }^{\dagger }f_{\mathbf {k-q} }\alpha _{\mathbf {q} })+g_{\mathbf {kq} }^{(1)}(f_{\mathbf {k} }^{\dagger }h_{\mathbf {k-q} }\beta _{\mathbf {q} }+h_{\mathbf {k-q} }^{\dagger }f_{\mathbf {k} }\beta _{\mathbf {q} }^{\dagger })]+H_{L}^{B}$

where $\epsilon _{1}=0,\epsilon _{2}=V^{\ast }d$ and the Hamiltonian $H_{L}^{B}$ is given by:

$H_{L}^{B}=E_{0}+\sum _{\mathbf {k} }(\omega _{\mathbf {k} }^{\alpha }\alpha _{\mathbf {k} }^{\dagger }\alpha _{\mathbf {k} }+\omega _{\mathbf {k} }^{\beta }\beta _{\mathbf {k} }^{\dagger }\beta _{\mathbf {k} })$

The operators $f_{\mathbf {k} }^{\dagger }$ and $h_{\mathbf {k} }^{\dagger }$ are the Fourier transforms of $f_{i}^{\dagger }$ and $h_{i}^{\dagger }$ respectively and where

$g_{\mathbf {kq} }^{(1)}=d{\sqrt {\frac {2}{N}}}t\gamma _{\mathbf {k-q} }u_{\mathbf {q} }$

$g_{\mathbf {kq} }^{(2)}=d{\sqrt {\frac {2}{N}}}t\gamma _{\mathbf {k} }v_{\mathbf {-q} }$

The two Dyson's equations in the non-crossing approximation are given as follows:

$G_{\nu }(\mathbf {k} ,\omega )={\frac {1}{\omega -\epsilon _{\nu }-\sum _{\mathbf {q} }{g_{\mathbf {kq} }^{(\nu )}}^{2}G_{\nu ^{'}}(\mathbf {k-q} -\omega -\omega _{\mathbf {q} }^{\mu })}}$

where the first equation is obtained for $\nu =1,\nu ^{'}=2\;\mathrm {and} \;\mu =\alpha$ and the second equation for $\nu =2,\nu ^{'}=1\;\mathrm {and} \;\mu =\beta$. The Green's function $G_{1}(G_{2})$ corresponds to the quasi-particles created by $h_{\mathbf {k} }^{\dagger }(f_{\mathbf {k} }^{\dagger })$.These equations can be solved iteratively starting from $G_{\nu }^{(0)}={\frac {1}{(\omega -\epsilon _{\nu }+i\eta )}}$.

In the calculations, we take $V^{\ast }=V=J,J_{xy}=2t,H=0\;\mathrm {and} \;\epsilon =0.1$.

NMR measurements indicate that for $^{3}{\textrm {He}}$ impurities in solid $^{4}{\textrm {He}}$ we should consider J/t >>1. In this figure, the spectral function $A(\mathbf {k} =0,\omega )$ is presented for the case of J/t = 3 (left) and J/t = 6 (right).We notice that for J/t = 3 the bandwidth $W_{A}$ of the substitutional impurity is small.For J/t = 6, $W_{A}$ is very small, i.e. $W_{A}/t\sim 10^{-3}$ and hence we only show the spectral function of the interstitial impurity for this value of J/t. We notice that the spectral function of the interstitial impurity has two main peaks, a lower frequency peak with small spectral weight and a higher frequency one with most of the spectral weight.

Edge-dislocations leading to topological glass phase

Inhomogenetities provided by $_{}^{3}{\textrm {He}}$ impurities provided by $_{}^{4}{\textrm {He}}$ solid nucleation process or by a relatively fast inhomogenous cooling process can create interstitial atoms.

It is known that the inhomogenous nucleation of solid $_{}^{4}{\textrm {He}}$ starts on the cell walls. We will assume that solid $I_{}^{4}{\textrm {He}}$ grows layer-by-layer on the surface of the cell for following reasons:

(a) The geometry of the cells used in the experiments is characterized by a large surface with small distance between large confining walls.

(b) The cooling of the solid is caused through cooling of these large surfaces, therefore, atoms near the surface will get cold first.

(c) Helium atoms at temperature $T\sim 1K$ get absorbed on the surface of most subtrates becuase of a relatively strong dipolar interaction with the surface.

In studies of $Insertformulahere$ on graphite for example and in all known substrates the first layer of absorbed $_{}^{4}{\textrm {He}}$ is solid. The second layer of $_{}^{4}{\textrm {He}}$ on the graphite surface is also solid at layer completion density. After the first or a few layers are deposited on the surface, the absorbed solid $_{}^{4}{\textrm {He}}$ is compressed relative to the liquid in contact and, therfore, the caoted surface provides a stronger attractive potential for an atom as compared to that provided by its surrounding atoms in the liquid; thus, the Nucleation of solid $_{}^{4}{\textrm {He}}$ had been a puzzle in the past just because of the large surface energy cost required in homogenous nucleation. In a layer-by-layer growth this is not an issue, becuase when the next layer is deposited, there is no additional surface area intrduced, namely, just the same-size interface advances.

It is believed that the solid/liquid interface in the presence of $_{}^{3}{\textrm {He}}$impurities becomes rough due to binding of such impurities to the interface. Even an extremely low impurity concentration, namely as low as 1 ppm, has a significant effect in this process. In this paper, it is proposed that the $_{}^{3}{\textrm {He}}$ impurities bind to defects namely to dislocation or disclinations, which are expected to form on the two dimensional solid/liquid interface. There are various theories of two dimensional melting, the most popular of which is the theory of Halperin, Nelson and Young which are inspired by the Kosterlitz-Thoules(KT) theory of vortices in superfluid films. According to this theory, the melting proceeds via two continuous KT transition, the lowest temperature one caused