Magnetic Semiconductors

motivation

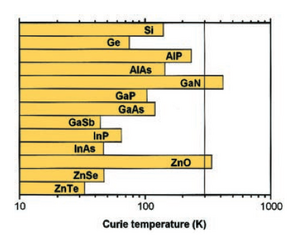
The observation of ferromagnetism in magnetic ion doped II–VI diluted magnetic semiconductors (DMSs), and later in (Ga,Mn)As materials has inspired a great deal of research interest in a field dubbed “spintronics” of late, which could pave the way to exploit spin in addition to charge in semiconductor devices. The main challenge for practical application of the DMS materials is the attainment of a Curie temperature at or preferably above room temperature to be compatible with junction temperatures. Zener's model of ferromagnetism, originally proposed for transition metals in 1950, can explain T C of Ga1− xMnxAs and that of its II-VI counterpart Zn1− xMnxTe and is used to predict materials with T Cexceeding room temperature, an important step toward semiconductor electronics that use both charge and spin..The particular predictions are predicated on the assumption that hole mediated exchange interaction is responsible for magnetic ordering. Among the additional advantages of ZnO- and GaN-based DMSs are that they can be readily incorporated in the existing semiconductor heterostructure systems, where a number of optical and electronic devices have been realized, thus allowing the exploration of the underlying physics and applications based on previously unavailable combinations of quantum structures and magnetism in semiconductors.

Diluted magnetic semiconductors

This family of materials encompasses standard semiconductors, in which a sizable portion of atoms is substituted by such elements, which produce localized magnetic moments in the semiconductor matrix. Usually, magnetic moments originate from 3d or 4f open shells of transition metals or rare earths (lanthanides), respectively, so that typical examples of diluted magnetic semiconductors (DMS) are Cd1-xCoxSe, Ga1-xMnxAs, Pb1-xEuxTe and, in a sense, Si:Er. A strong spin-dependent coupling between the band and localized states accounts for outstanding properties of DMS. This coupling gives rise to spin-disorder scattering, giant spin-splittings of the electronic states, formation of magnetic polarons, and strong indirect exchange interactions between the magnetic moments, the latter leading to collective spin-glass, antiferromagnetic or ferromagnetic spin ordering. Owing to the possibility of controlling and probing magnetic properties by the electronic subsystem or vice versa, DMS have successfully been employed to address a number of important questions concerning the nature of various spin effects in various environments and at various length and time scales. At the same time, DMS exhibit a strong sensitivity to the magnetic field and temperature as well as constitute important media for generation of spin currents and for manipulation of localized or itinerant spins by, e.g., strain, light. Electrostatic or ferromagnetic gates. These properties, complimentary to both non-magnetic semiconductors and magnetic metals, open doors for application of DMS as functional materials in spintronic devices.

magnetic impurities in semiconductors

we can describe the DMS according to the model in which the electron states can divided in to two categories:

(i) localized magnetic d or f shells (ii) extended band states built up of s, p, and some times d atomic orbitals

The starting point for developing a useful predictive model of (III-Mn)V ferromagnetism is understanding of the electronic state with the single Mn impurity in the host lattice. we need to understand the charecter of Mn local moments before we explein how these isolated local moments are coupled. Ao we discuss the property of Mn impurity in GaAs and on the nature of ferromagnetic coupling in (Ga, Mn)As.

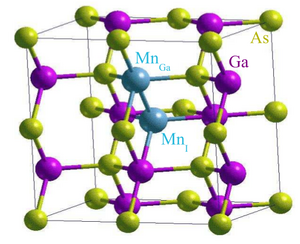
Between (III,V) hosts, Mn impurity has been studied in GaAs. The elements in the (Ga,Mn)As compound have nominal atomic structures:

[Ar]3d10 4s2 p1 for Ga

[Ar]3d5 4s2 for Mn

[Ar]3d10 4s2 p3 for As

This circumstance correctly suggests that the most stable and therefore most common position of Mn in the GaAs host lattice is on the Ga site where its two 4s electrons can participate in crystal bonding in much the same way as the two Ga 4s electrons. The substitutional MnGa , and the less com- mon interstitial MnI , positions are illustrated in Fig. 1. a The MnGa impurity can be as an acceptor Because of the missing valence 4p electron. In the electrically neutral state, labeled as A0 (d5 + hole), Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Mn_{Ga}} has the character of a local moment with zero angular momentum and spin S = 5/2 and a moderately bound hole.Since The local moment is formed by three occupied sp-d bonding states with dominant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{2g}} (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3d_{xy}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3d_{xz}} ,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3d_{yz}} ) character and by two occupiedFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_{g}} (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3d_{x^{2}-y^{2}}} ,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3d_{z^{2}}} ) orbitals that are split from the sp-d states by the tetrahe-orientation and together comprise the S = 5/2 local mo- ment. The weakly bound hole occupies one of the three antibonding sp-d levels with dominant As 4p character. The charge −e ionized Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MN_{Ga}} acceptor center, labeled as A−(d5 ), has just the S = 5/2 local spin character.

Fig. 1.A: substitutional MnGa in GaAs.

Fig. 1.B :Two Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_{g}} 3d orbitals and three Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{2g}} 3d orbitals of Mn..

p-d exchange coupling

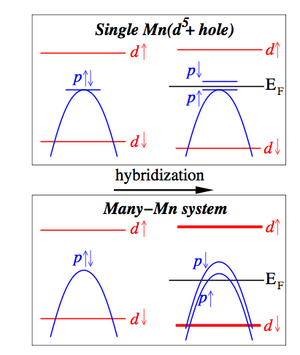
The top of the GaAs valence band is dominated by 4p levels which are more heavily weighted on As than on Ga sites. Direct exchange between holes near the top of the band and localized Mn d electrons is weak since MnGa and As belong to different sublattices. This fact allows p-d hybridization to dominate, explaining the antiferromagnetic sign of this interaction (Bhattacharjee et al., 1983) seen in experiment (Okabayashi et al., 1998).

There is a simple physical picture of the p-d exchange interaction which applies when interactions are treated in a mean-field way, and therefore also applies as an interpretation of LSDA calculations. Given that the filled, say spin-down, Mn d-shell level is deep in the valence band and that the empty spin-up d level is above the Fermi level and high in the conduction band, hybridization pushes the energy of spin-down valence-band states up relative to the energy of spin-up valence-band states. The resulting antiferromagnetic coupling between valence-band states and local Mn spins is illustrated schematically in Fig. 2. The same basic picture applies for itinerant valence-band states in a heavily doped metallic DMS and for the acceptor state of an isolated MnGa impurity. Note that the cartoon band structure in Fig. 5 is plotted in the electron picture while the DMS literature usually refers to the antiferromagnetic p-d coupling between holes and local Mn moments.

Fig. 2:Splitting of the isolated Mn acceptor level (top panel) and of the top of the valence band in the many-Mn-atom system (bottom panel) due to p-d hybridization.

Ab-initio calculation for Mn in DMS

In SDF theory (Hohenberg and Kohn, 1964; Kohn and Sham, 1965) many-body effects are buried in a complex Sham, 1965) many-body effects are buried in a complex exchange-correlation energy functional. Once an approximation is made for this functional, predictions for electronic and magnetic properties depend only on the particular arrangement of atomic nuclei under consideration The exchange-correlation energy functional leads to a self-consistently determined spin-dependent exchange-correlation potential that appears in an effective independent-particle Hamiltonian. The main technical challenge in DFT applications is the development of numerically efficient methods that provide accurate solutions of single-body Schr¨odinger equations (see review articles (Jones and Gunnarsson, 1989; Sanvito et al., 2002)). DFT Uses the charge density as the fundamental system variable, and describes the ground state properties by using certain functional of the charge density. the advantage of this method is solvingSimply the many body problem by using the electron charge density as fundament variable rather than the wavefunction. However, the major limitation for applying this method is this is only Applicable for the ground state, needs approximation for exchange-correlation energy functional which is unknown.

so, we can apply some successful Approximation for exchange-correlation energy:

LDA

The local density approximation is For regions of a material where the charge density is slowly varying, the local charge density can be considered to be the density of an equivalent uniform homogeneous electron gas. We can produces moderately accurate results in most cases. However, the weakness of this approximation is we cannot predict atomic ground state energies and ionization energies, and overpredicts binding energies.

LSDA

LSDA predictions for spectral properties, like the local DOS, are less reliable than predictions for total-energy related properties. This is especially true for states above the Fermi energy, and is manifested by a notorious in accuracy in predicting semiconductor band gaps. From a DFT point of view, this inconsistency arises from attempting to address the physics of quasiparticle excitations using ground-state DFT. In Mn-doped DMSs, the LSDA also fails to account for strong correlations that suppress fluctuations in the number of electrons in the d shell. One generally accepted consequence is that the energy splitting between the occupied and empty d states is underestimated in SDF theory, leading to an unrealistically large d-state local DOS near the top of the valence band and to an overestimate of the strength of the p-d exchange.

Infact, The many-body effects of the complicated quantum mechanical problem are buried in the so-called exchange-correlation part of the energy functional Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{xc} [n(r), m(r)]} . The exact solution is intractable for macroscopic systems and some approximation must be made.

The local approximation (LSDA) takes as its starting point the energy of a uniformly spin-polarized homogeneous electron gasFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon _{x,c}(n(r),\left | m(r) \right |)} so thatFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{x,c}} can be written in the form

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{x,c}[n,m]\approx \int dr n(r)\varepsilon _{x,c}(n(r),\left | m(r) \right |)}

The functional derivative of this quantity with respect to m(r) provides the effective magnetic fields for the single- electron equations, namely the spin-polarized band structure.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v^{eff}[n,m;r]=V^{ext}(r)+e^{2}\int dr^{'}\frac{n(r)}{\left | r-r^{'} \right |}+\frac{\delta E_{xc}}{\delta n(r)}[n,m]}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^{eff}[n,m;r]=B^{ext}(r)+\frac{\delta E_{xc}}{\delta n(r)}[n,m]}

whereFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V^{ext}(r)} describes an external potential such as a lattice array of nuclei and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B^{ext}(r)} an external magnetic field. The electron density and magnetization are given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n(r)=\int^{\varepsilon _{f}}d\varepsilon \sum_{i}tr(\varphi^{\ast }_{i}(r,\varepsilon )\varphi_{i}(r,\varepsilon ))}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m(r)=\int^{\varepsilon _{f}}d\varepsilon \sum_{i}tr(\varphi^{\ast }_{i}(r,\varepsilon )\sigma \varphi_{i}(r,\varepsilon ))}

where theFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi_{i}(r,\varepsilon )} obey the Schrodinger–Pauli [(Kohn– Sham) equation]

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-\triangledown ^2+v^{eff}(r)-\sigma .B^{eff}(r)\varphi_{i}(r,\varepsilon)=\varepsilon\varphi_{i}(r,\varepsilon)}

comparision of magnetic intraction

RKKY intraction

Indirect exchange coupling of magnetic moments over relatively large distance via band electrons due to the Coulomb exchange. It becomes efficient when a high concentration of free carriers is present such as in metals for which it was developed.

Direct superexchange

Direct coupling of magnetic ions through verlap of magnetic orbitals.

Indirect superexchange

Spins of two magnetic ions are correlated due to the exchange interaction between each of the two ions and the valence p-band.

Double exchange

exchange mechanism for the carrier-induced ferromag Couples magnetic ions in different charge state by virtual hopping of the ‘extra’ electron from one ion to the other through interaction with p-orbitals.

Zener model

Zener in 1950 demonstrated that thethe spin coupling between incomplete d shells and condunction electrons leads to the tendency for the ferromagnetic alignment od d spins. The occurance kof ferromagnetism or antiferromagnetism in various system is understood. according to this paper the relative magnitude of three types of coupling determine the type of magnetic behavior. The first coupling arises from the direct exchange between incomplet d shells of nearest neigbors. If we are intrested in the variation of this exchange energy only with the degree of ordering of the net spins of d shells,we can show this energy as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}\alpha s_{d}^{2}} per atom. hereFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_d} is the mean componet per atom of the net spin of the d shells along the direction of magnetization.Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} is positive. so its magnitude rapidly decreases with a decreasing amount of overlap of d shells of adjacent atoms. the second spin coupling arises from the exchange couplingbetween conduction electrons and the inner d electrons. this energy can be represent as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta s_{d} s_{c}} per atom.where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_c} is the net magnetization of the conduction electrons,expressed in units of Bohr magnetos per atom. The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} is positive and it is in the order of magnitude of electron volt.

The tird spin coupling arises from the fermi kinetic energy of the conduction band. Since the increase in the fermi kinetic energy is related to an unbalanced disturbution of conduction electrons,it must be an an even function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{c}} so we can represent this increase in energy byFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}\gamma s_{c}^2 } per atom. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} can be represented in terms of the kinetic energy at the top of teh band and the number of electrons per atom. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma=\frac{2\epsilon }{3n} } so the total spin energy can be written in the following form:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{spin}=\frac{1}{2}\alpha s_{d}^{2}+\beta s_{d} s_{c}+\frac{1}{2}\gamma s_{c}^2 }

since the contribution of conduction electrons is negligible, we can get the equiblirium value for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{c}} when minimize energy

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{c}=\frac{\beta }{\gamma }S_{d}} by subtituation of the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{c}} we can get:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{spin}=\frac{1}{2}{(\alpha -(\beta ^{2}/\gamma)})S_{d}^{2}}

the coefficient of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha -(\beta ^{2}/\gamma)} corresponds to the inner field of weiss.Thus, the type of the magnetic behavior is determined by the relative magnetitude of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta ^{2}} andFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \gamma}

For ferromagnetism Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta ^{2}>\alpha \gamma}

For antiferromagnetismFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta ^{2}<\alpha \gamma}

although this peper does not develop the quantitative theory of ferromagnetism, it is enough to notice that the order of ferromagnetic coupling term. according to this theory it is in the order of magnitude of a teth of an ev per atom while the observed magnetization is not in this order.The power of this theory is in predicting the magnetic behavior of systems qualitatively. Ferromagnetism will be observed in all systemsfor which the first equation is satisfied. In these systems nighboring incomplete d shells are sufficiently far apart so the indirect intraction via the conduction electrons dominates over the direct antiferromagnetic coupling. The large distance of separation between incomplete d shells insures the ferromagnetism only when condunction electrons providethe necessary ferromagnetic coupling.

Why the Zener model is equivalent to RKKY interaction

The basic idea behind the RKKY interaction is based on the exchange coupling between the magnetic ion and the conduction band electrons. It should be mentioned that s and d wave functions are orthogonal and would not lead to any interaction in perfect one electron system. The conduction electron is magnetized in the vicinity of the magnetic ion, with the polarization decaying with distance from the magnetic ion in an oscillatory fashion(Friedel oscillation). This oscillation causes an indirect super-exchange interaction (RKKY)between two magnetic ions on the nearest or next near- est magnetic neighbors. This coupling may result ina parallel (ferromagnetic) or an anti-parallel (antiferromagnetic) setting of the moments dependent on these paration of the interacting atoms.

Dietl et al [reference]have shown that double exchange cannot lead to carrier induced ferro-magnetism for carrier densities lower than metals in Mn based III-V DMSs,and proposed the zener Model based on ferromagnetic interaction mediated by free carriers in tetrahedrally coordinated semiconductors. In the Zener model since the Mn d shell is half filled, the direct interaction between d shells of the adjacent Mn atoms lead to an antiferromagnetic configuration of d sell spins.On the other hand, the indirect coupling of spins through the conduction band tends to align the spin of the incomplete d shells in a ferromagnetic manner.

However, this model was later abandoned, as neither the itinerant character of the magnetic electrons nor the quantum (Friedel) oscillations of the electron spin polarization around the localized spins were taken into account; both of these are now established to be critical ingredients for the theory of magnetic metals. We emphasize that in the case of semiconductors, however, the effect of the Friedel oscillations averages to zero because the mean distance between the carriers is greater than that between the spins. Under such conditions, the exchange interaction mediated by the carriers is ferromagnetic for most of the spin pairs, which reduces the tendency toward spin-glass freezing. In fact, for a random distribution of the localized spins, the mean-field value of the Curie temperature T C deduced from the Zener model is equal to that obtained from the Ruderman, Kittel, Kasuya, and Yosida ͑RKKY͒ approach, in which the presence of the Friedel oscillations is explicitly taken into account. So Zener model becomes equivaent (13) to the approach developed by Ruderman, Kittel, Kasuya, and Yosida (RKKY), in which the presence of the oscillations is taken explicitly into account.

Mean field zener model

We can apply the zener Model of carrier-controlled ferromagnetism by introducing the functional of free energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F[M(r)]} . selecting theFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(r)} as an order parameter means that the spins are treated as classical vectors. The starting point of the model is to determine how the Ginzburg-Landau free-energy functional F depends on the magnetization M of the localized spins. The hole con- tribution to F, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{c}[M(r)]} , is computed by diagonalizing the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6\times 6} Kohn-Luttinger matrix together with the p-d exchange contribution, which will be discussed in more details in the part of k.p model for energy band calculation.

In the case of magnetic semiconductors

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F[M(r)]=F_{s}[M(r)]+F_{c}[M(r)]}

which is consits of two terms, and describes the free energy of the Mn spins in the absence of the carier and the cariers in the presence of the spins. the dynamics of spins in the absence of the carier is supposed to be slower than that of the cariers.In addition, in the sprit of the molecular field approximation, the classical field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(r)} controls the effect of the spins upon the carriers.

The thermodynamic of the system is described by partition functionZ

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=e^{(-\int dr F[M(r)]/k_{B}T)}}

In mean field approximation a term which is corresponding to the minimum of $F[M(r)]$can determine Z with enough accuracy. In the case of uniform magnetization M, the spin part of the free energy in the presense of magnetic field H can be written: $F_{s}[M]=\int _{0}^{M}dM_{0}h(M_{0})-MH$

Here $h(M_{0})$ denotes the inverse function to $M_{0}(H)$, which is experimentally available in the absence of the carriers and in the field h and tempreture T.

It is convenient to parametrize the dependence of magnetization on the magnetic field in the absence of the carriers, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(H)} by the Brillouin function[1] $B_{s}$

$M_{0}(T,H)=Sg\mu _{B}N_{0}x_{eff}B_{s}(Sg\mu _{B}H/k_{B}(T+T_{AF}))$

where two empirical parameters, the effective spin concentration $x_{eff}N_{0}<xN_{0}$, and tempreture $T_{eff}>T$take the presence of the superexchange antiferromagnetic interactions into account.[ Y. Shapira, S. Foner, P. Becla, D. N. Domingues, M. J. Naughton, and J. S. Brooks, Phys. Rev. B 33, 35(198).]

Near $T_{c}$ and for $H=0$. M is sufficiently small to take $M_{0}(T,H)=\chi (T)h$ where $\chi (T)$ is the magnetic susceptibility of localized spin in the absense of the carriers. Under this conditions:

$F_{s}[M]=M^{2}/2\chi (T)$

Since the valence band originates merely from the anion p and cation d wave functions, the exchange interaction mediated by holes is expected to be strongly affected by anisotropy of hole dynamics and the coupling between the spin and orbital degrees of freedom. To take those effects into account, the hole dispersion and wave functions are computed by diagonalizing the $6\times 6$Kohn-Luttinger k • p matrix.

k.p Model for Energy Band Calculations

For the time being, let us say, we want to calculate the bands in a bulk semiconductor. We start with time independent Schrodinger's equation. But from the periodicity of the crystal we already know that the eigen energy states has to be the Bloch states. So let us substitute theFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi _{n,k}=u_{n,k}e^{ik.r}} into the Schrodinger's equation in order to obtain a equivalent differential equation in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{n,k}} . Next we convert this continuous space variable differential equation into a discrete matrix equation by expanding the periodic Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{n,k}} into complete set of periodic functions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{n,0}} (They are orthogonal, they are infinite in count, but still I am not sure if one can theoretically prove that they form a complete set for expanding any periodic function of period R). The general form of the matrix is as follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} E_{1,0}+\frac{\hbar^{2}k^{2}}{2m}+\frac{\hbar}{m}k.P_{1,1}&\frac{\hbar}{m}k.P_{1,2} & \frac{\hbar}{m}k.P_{1,3}&... &... \\ \frac{\hbar}{m}k.P_{2,1}& E_{2,0}+\frac{\hbar^{2}k^{2}}{2m}+\frac{\hbar}{m}k.P_{2,2}&\frac{\hbar}{m}k.P_{2,3}& ...&.... & \\ \frac{\hbar}{m}k.P_{3,1}&\frac{\hbar}{m}k.P_{3,2} &E_{3,0}+\frac{\hbar^{2}k^{2}}{2m}+\frac{\hbar}{m}k.P_{3,3} &... & ...\\ ... & ... &... & ... & \\ ...& ... & ... &... & \end{pmatrix}}

WhereFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{n,m}} is the momentum matrix element Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle u_{n,0}\left | -i\hbar\nabla \right |u_{m,0} \right \rangle} .

First of all note thatFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k.P_{n,n}} terms is a vector dot product. Note thatFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k.P_{n,m}} terms, which are linear in k, are spread all over the matrix. Rest of the terms, which are either constant or quadratic in k, are only along the diagonal. One can either try to solve this matrix rigorously (obviously in finite basis approximation) or one can use the time independent per- perturbation theory to obtain solution to any given order of accuracy. (So, we can safely claim that perturbation theory involves more approximations the finite basis approximation). Under the perturbation theory the unperturbed Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}} is the diagonal matrix containing the unperturbed eigen-energies. 'Perturbation' is sum of a diagonal matrix containing the square term and a matrix containing the linear terms.

As one moves away from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=0} the 'perturbation' increases. Till the zeroth order energies are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n,k}=E_{n,0}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{n,k}=u_{n,0}} .Til first order

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n,k}=E_{n,0}+\frac{\hbar}{m}k.P_{n,n}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{n,k} =u_{n,0}+\sum_{m}(\frac{k.P_{m,n}}{m(E_{n}-E_{m})})}

Till the second order

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n,k}=E_{n,0}+\frac{\hbar}{m}k.P_{n,n}+\frac{\hbar^{2}k^{2}}{2m}+\sum_{m}(\frac{\hbar k.P_{m,n}}{m(E_{n,0}-E_{m,0})})^{2}}

One usually do not need to calculate the wavefunction till second order. Strength of the k.p theory is based on the fact that at the band edges the unit cell functions are very symmetric and and hence lot of terms Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k.P_{i,j}} are zero. Also only those bands mix considerably whose energiesFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n,0}-E_{j,0}} are close.

Spin orbit coupling

There is an important point that I skipped above.I pointed out that spin orbit coupling is important for calculations of valance band structures. But we didn't include that in the Schroedinger's equation above. If we do include the spin orbit term in the Hamiltonian, the matrix above would contain two more terms added to all the matrix elements - Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\nabla V)x(P.\sigma)_{n,m}+(\nabla V)x(k.\sigma)_{n,m}} Note that p operator when operated is the atomic potential and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} is the Dirac spin matrix. over unit cell functions would give us momentum numbers multiplied by the wave function. These momentum numbers are usually much much higher than k. Hence second term, which is called k -dependent spin orbit term is always neglected. Hence we only get a constant energy term spread out all over the matrix (definitely based on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p.\sigma_{n,m}} being nonzero). For all the models to come, other than the Kane Model, people usually keep the constant energy shift in one of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n.0}} which is called spin-spit off band. Spin terms is not added to any other elements of the matrix.

Kane Model

Kane Model solves the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k.p} matrix using finite basis method (and not the perturbation approach) by including just the 4x2 most significant bands. It includes the spin-orbit term.(Above matrix with the spin terms is Kane matrix) It uses the above mentioned symmetriesfor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{n,k=0}(r)} and uses the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid j,m_{j}>} all these matrix element can be evaluated easily. When the obtained results are compared with the experimental results we realize that these 4 bands are not sufficient. Following are the main results

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigstar} We obtain four doubly degenerate bands. But remember its not simply "spin degeneracy". Only the two degenerate conduction bands have different spins. Rest all the three doubly degenerate valance bands have mixed spins. What I mean is that none of the two bands lh1and lh2 have definite spins. Similar is the situation with the hh and split-off bands. This it seems is expected. Because states of definite angular momenta are also going to be the states of definite energies; and states of definite angular momenta going to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid j,m_{j}>} which does not have definite spin.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigstar} It gives wrong heavy hole mass. Its just equal to the free electron mass and also band is curved up.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigstar} It predicts the relationship between Eg and effective masses. lh effective mass is proportional to Eg whereas e effective mass is nearly proportional to Eg provided that split-off energy is much more than Eg .

Luttinger-Kohn Models

LK model uses only 3x2 valance bands directly. It includes the effect of conduction band(one can easily incorporate the effects of more than one extra band also) through Lowdin Re-normalization.it uses the same Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid j,m_{j}>} basis.. The result of applying Lowdin's Re-normalization is very simple.Instead of having Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar}{m}k.P_{j,j'}} we now have termsFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\gamma }(\frac{\hbar}{m}k.P_{j,\gamma })(\frac{\hbar}{m}k.P_{\gamma,j' })/(E_{0}-E_{\gamma ,0})} spread all over the metrix. Note that the j is the row index and j' is the column index whereasFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} is the index of the band being considered separately. Note this term can be written in Cartesian coordinates asFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\alpha \beta }\sum_{\gamma }(\frac{\hbar^{2}}{2m})\frac{2(k^{\alpha })(k^{\beta })(P_{j,\gamma}^{\alpha })(P_{\gamma,j'}^{\beta })}{m(E_{0}-E_{\gamma,0})}} remember that apart from this we also had Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{j,0}+\hbar^{2}k^{2}/2m} along the diagonals.Hence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\alpha \beta }\sum_{\gamma }(\frac{\hbar^{2}}{2m})\frac{2P_{j,\gamma}^{\alpha }P_{\gamma,j'}^{\beta }}{m(E_{0}-E_{\gamma,0})}+\frac{\hbar^{2}}{2m}\delta _{\alpha,\beta }\delta _{j,j' }} is the coefficient of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{\alpha}k_{\beta}}

These are all k-dependent terms. we call this coefficient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{j,j'}^{\alpha ,\beta }} . Hence any generic term of Luttinger-kohn Hamiltonian can be written asFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{j,j'}=D_{j,j'}^{\alpha ,\beta }k_{\alpha ,\beta }E_{j,0}\delta _{j,j'}}

For Zinc Blend and Diamond crystals theseFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{j,j'}^{\alpha ,\beta }} coefficient can easily be evaluated using the symmetry properties of S and P orbitals. Each of these terms are then rewritten as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar^{2}}{2m}\gamma K_{\alpha } K_{\beta }} are called Luttinger parameters. In fact we need just three of these. The final matrix equation involves three Luttinger parameters - Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma_{1}, \gamma_{2},\gamma_{3}} In theory they are just some matrix elements between various bands but in practice they are treated as adjusting parameters in order to obtain the band profiles observed experimentally.

I cannot go to more details here; however, you can find two following links: Hole-mediated ferromagnetism in tetrahedrally coordinated semiconductors T.Dietl refrenceT.Dietl H.Ohno and F. Matsukura 3 Phys. Rev. Lett. 63, 195205, 2001 [2]

In the appendix B of the first link you can see the numerical procedure to evaluate Helmholts free energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{c}} at given hole concentration p as a function of the Mn magnetization M

---

calculation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{c}}

Now, we can back to The free energy density which consists of two terms as discussed before. The Luttinger-kohn model supplemented by the p-d exchange provides the direct influence of the magnetic field on the hole spectrum. Furtheremore, carrier- carrier spin correlation was described by inrtiducing a fermi liquid-like parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{f}} , which enlarges the pauli susceptibility of the hole liquid. No disorder effect were taken into account on the ground that their influence on termodynamic properties is weak except for strongly localized regime.

After having the hole energies , the free energy density $F_{c}(M)$was evaluated according to the procedure suitable for fermi liquid of arbitrary degeneracy.By minimizing

$F[M(r)]=F_{s}[M(r)]+F_{c}[M(r)]$ respect to M at given T,H, and hole concentration p, Mn spin magnetization $M(T,H)$ was obtained as a solution of mean field approximation.

$M(T,H)=x_{eff}N_{0}g\mu _{B}SB_{s}[g\mu _{B}(-\partial F_{c}[M]/\partial M+H)/k_{B}(T+T_{AF})]$ Where pecularities of valence band structure, such as the presence of various hole subbands, spin orbit coupling are hidden in$F_{c}[M]$.

Near the curie tempreture $T_{c}$ and H=0, where M is small we expect

$F_{c}[M]-F_{c}[0]~-M^{2}$

this is convenient to parametrize this dependence by the generalized carrier spin susceptibility ${\tilde {\chi }}_{c}$which is related to magnetic susceptibility of the carrier liquid according to ${\tilde {\chi }}_{c}=A_{F}(g*\mu _{B})^{2}\chi _{c}$in terms of ${\tilde {\chi }}_{c}$

$F_{c}[M]=F_{c}[0]-A_{F}{\tilde {}}\chi _{c}\beta ^{2}M^{2}/2(g\mu _{B})^{2}$

By expanding $B_{s}(M)$ for small M one arrives to the mean field formula for $T_{c}=T_{F}-T_{AF}$, where $T_{F}$is given by

$T_{F}=x_{eff}N_{0}S(S+1)A_{F}{\tilde {\chi _{c}}}(T_{c})\beta ^{2}/3k_{B}$ For a strongly degenerate carrier liquid$\left|\epsilon _{F}\right|/k_{B}T\gg 1$ , and neglecting the spin-orbit interaction, $\rho _{s}$ becomes equal to thtotal density of states $\rho$ for intraband charge excitations,

where, $\rho =m_{DOS}^{*}k_{F}/\pi ^{2}\hbar ^{2}$

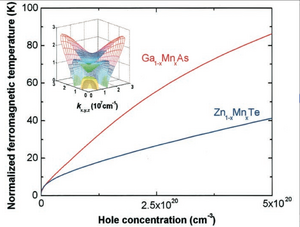
In order to check the quantitative significance of carrier entropy, the computed values of $T_{c}$ were compared to those obtained assuming strong degeneracy of the carrier liquid. As shown in Fig. 3 such an assumption leads to error smaller than 1% if $\left|\epsilon _{F}\right|/k_{B}T\gg 10$. Thus, in this range, the carrier energy, not the free energy, was used for the evaluation of$T_{c}$.Furthermore, we take $x_{eff}=x$and $T_{AF}=0$ , as discussed above.

The value of $T_{c}$has been shown for p-(Ga,Mn)As and p-(Zn,Mn)Te (Fig. 4). The results confirm an expected strong dependence of $T_{c}$ on x and p. At a given p, the magnitude of $T_{F}$ is substantially greater in the case of p-(Ga,Mn)As. This is mainly caused by the smaller value of the spin-orbit splitting between the $\gamma _{7}$, and$\gamma _{8}$ bands in arsenides, $\Delta _{0}=0.34ev$

in comparison with that of tellurides,$\Delta _{0}=0.91ev$.

Fig. 4: Normalized ferromagnetic temperature $T_{F}$ as a function of hole concentration. Inset shows an example of the cross section of the Fermi volume of holes in a ferromagnetic zinc-blende semiconductor: Nonzero magnetization leads to a splitting of the valence band into four subbands. This complex valence-band structure was used to determine the mean-field values of $T_{F}$for $p-Ga_{0.95}Mn_{0.05}As$ and $p-Zn_{0.95}Mn_{0.05}Te$ (solid lines) and to establish the chemical trends depicted in Fig. 5

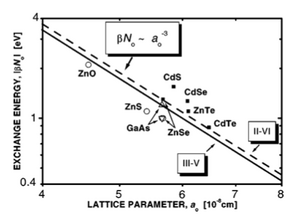
This is important to extend oure theoretical result of x,$\beta$,or $A_{F}$because the $T_{c}$ is directly propertional to them. Here, we are not going to discuss material parameter extensively; however, the value of exchange integral will be discussed. the Curie temperature is proportional to the square of the p-d exchange integra$\beta$. Figure 5 presents the magnitudes of the exchange energy $\beta N_{0}$ as determined by photoemission and magneto-optical studies for various DMS containing about 5% of Mn. The values of $\beta N{0}$ are seen to increase when the lattice parameter decreases. This trend stems from the corresponding changes in the charge-transfer and correlation energies as well as from a dependence of the p-d hybridization energy on the bond length b.[ T. Mizokawa, J. Okabayashi, T. Nambu, and A. Fujimor 1995]

Thus, in order to obtain the values of $\beta N_{0}$ for materials for which no direct determination is available, guided by the results presented in Fig. 15, we assume $\beta N_{0}=a_{0}^{-3}$. More explicitly, for groups III-V and IV semiconductors we take

$\beta _{III,V}=\beta (GaMNAs)$ and similarly $\beta _{II,VI}=\beta (ZnMNSe)$

Fig. 5: Energy of p-d exchange interaction for various materials containing 5% of Mn in cation sites as a function of lattice parameter. The values shown by solid squares were determined from excitonic splittings in the magnetic fiel[Refs. 22, 42, 72] while the empty symbols denote values evaluated from photoemission data [ 24 and 7].

Fig. 6:.is determined by a Computed values of the Curie temper- ature $t_{c}$for various p-type semiconductors containing 5% of Mn and $3.5\times 10^{20}$ holes per $cm^{3}$.

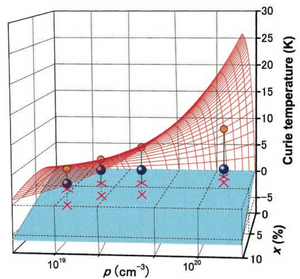
The data (Fig. 6) demonstrate that there is much room for a further increase of $T_{c}$ in p-type magnetic semiconductors. In particular, a general tendency for greater $T_{c}$ values in the case of lighter elements stems from the corresponding increase in p-d hybridization and reduction of spin-orbit coupling. We believe that this tendency is not altered by the uncertainties.

agreement between our theoretical result and experiment

The agreement between experiment and theory for $T_{c}$ and the magnetic anisotropy demonstrates that the present model, developed with no adjustable parameter, explains quantitatively the ferromagnetism observed in (Ga,Mn)As as well as the striking difference between T C values in (Ga,Mn)As and p-(Zn,Mn)Te. It also suggests that $T_{c}$ values above 300 K could be achieved in $Ga_{0.9}Mn_{0.1}As$ if such a large value of x could be accompanied by a corresponding increase of p.

Fig. 7: Curie temperature $T_{c}$ in $Zn_{1-x}MN_{x}-Te:N$for various Mn contents x and hole concentrations p deduced from the Hall resistance at 300 K. The plane with upper crosses corresponds to $T_{c}=0$. Experimental values are marked by blue spheres (22) and theoretical predictions by the red mesh and attached yellow spheres. $T_{c}$ is determined by a competition between the hole-induced ferromagnetic interactions (characterized by $T_{F}$ depicted in Fig. 4) and the antiferromagnetic interactions, described by$T_{AF}$ shown byby the plane with lower crosses.