Charge Density Wave

Introduction

Charge Density Wave (CDW) is a spatial modulation of the conduction electron density in a metal and an associated modulation of the lattice atom positions [1]. In the relation to the symmetry breaking, CDW is a broken symmetry state of metals brought by the electron-phonon interactions whose ground states are the coherent superposition of electron-hole pairs, and it displays spatial variation (translation symmetry is broken here just like any other spatially periodic structure) [2].

CDW states was first discussed by Frohlich in 1954 and by Peierls in 1955. [3, 4]

The latter pointed out that a one-dimensional metal coupled to the underlying lattice is not stable at low temperatures [5]. The ground state of the coupled electron-phonon system is characterized by a gap in the single-particle excitation spectrum and by a collective mode formed by electron-hole pairs involving a wave vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = 2k_F \!} with the charge density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(\vec{r})=\rho_0 + \rho_1 cos(2\vec{k_F} \cdot \vec{r}+\phi)} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_0 \!} is the unperturbed electron density of the metal and the condensate is called the charge density wave [5]. As with the superconductivity, CDW has a complex order parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta e^{i\phi} \!} with the magnitude of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \!} determines the size of the electronic gap and the amplitude Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta u \!} of the atomic displacements.[] The phase Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi \!} determines the position of the CDW relative to the underlying lattice [1].

Materials

CDW primarily exists in the low-dimensional metals, that is metals whose Fermi surfaces exhibit high anisotropy (metal is defined as an object in which the Fermi surface exists). This anisotropy is the answer to the question why the conductivity along one axis is higher than it is in any other axis, hence although the material itself appears to be 3 dimensional, the conductivity is appreciable only along a certain plane or a certain axis. The materials are typically conducting polymers, or also known as synthetic metals.

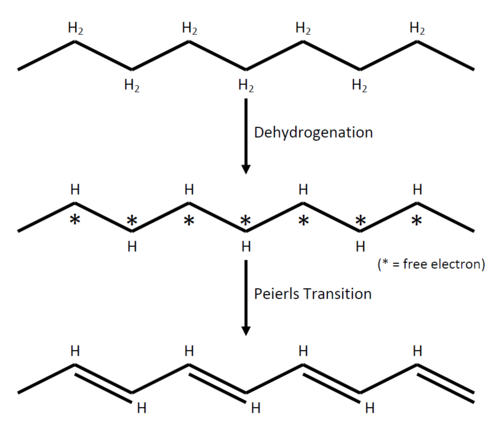
Following [6], as a simple picture of how the CDW comes into the system, let's consider a thought experiment about making a polyacetylene out of polyethylene (although not so realistic) as shown in figure 1.

Figure 1. Dehydrogenating a polyethylene and the polyacethylene that follows from Peierls transition

This configuration with many free electrons is unstable because, of course, it is energetically unfavoured. For now, let's assume it is possible to make such a reaction and hold it "stable" for a while for observation. What we have after dehydrogenating the polyethylene is basically a metal (just looking at the free electrons). That being a metal, as we shall see later exhibits the so called nesting of the Fermi surface which gives rise to many interesting phenomena in the low dimensional metals, for example Kohn anomaly  ???, Peierls transition, and density waves. Peierls transition deforms the lattice and an alternation of the double and single bonds will occur, producing polyacethylene.

The double bonds is, naturally, stronger than the single bonds which results in the double bonds being shorter than the single bonds. The difference in the bond length implies that the charge density changes when one is moving along the axis. The alternation of the bonds gives the spatial variation.

Therefore, with this rather oversimplified picture, we see how the CDW develops.

Density Of States (DOS) of a 1-D Electron Gas (1DEG)

Fermi surface of a 1DEG consists of 2 sheets with a distance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2k_F \!} apart, located at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm k_F} . The k-space DOS for 1DEG is just Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L/2\pi \!} and the number of states is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L/2\pi \times 2k_F = L k_F / \pi \!} . The 2 orientations of the spin, when taken into account, gives a factor of 2, so the total number of states (or the number of electrons) is : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = \frac{2 L k_F}{L}}

And the Fermi wave vector is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F = \frac{N \pi}{2L}}

The Fermi energy is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}_F = \frac{\hbar^2}{2m} k_F^2 = \frac{\hbar^2}{2m} \left(\frac{N \pi}{2L}\right)^2\!}

The density of states of one spin is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} n(\mathcal E) &= \frac{L}{2 \pi} \int dk \delta \left(\mathcal{E} - \frac{\hbar^2 k^2}{2m}\right) \\ &= \frac{L}{2\pi} \sum_{i=1}^2 \int dk \frac{\delta \left(k - \sqrt{\frac{2m \mathcal{E}}{\hbar^2}} \right)}{\left|\frac{\hbar^2 k_i}{m}\right|}\\ &= \frac{L}{2\pi}\left|\frac{m}{\hbar^2 k}\right|\\ &= \frac{L}{\pi \hbar}\sqrt{\frac{m}{2 \mathcal{E}}} \end{align} \!}

The result of our calculation shows that [7] :

1. We have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F = \frac{N \pi}{2L} \!} if N = 2 we will have a full band. Therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F = \pi / L \!} gives an insulator (or intrinsic semiconductor). At this point, we shall consider Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n < 2/L} so the system is metallic. Periodic potential contribution will be considered later.

2. The DOS is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E^{-1/2} \!} , while it is constant and proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E^{1/2} \!} in the 2D and 3D system, respectively. Therefore, some quantities having a factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d n(\mathcal{E})/d\mathcal{E} \!} changes sign going from 3D to 1D.

3. 1DEG Fermi wave vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F ~ n \!} , while in 2D and 3D it is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{1/2} \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{1/3} \!} , respectively.

4. When the electron changes state by interacting with phonons, the only possible transition is from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F \!} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -k_F \!} and vice versa by the conservation of energy and momentum.

Response Function of One-Dimensional Electron Gas (1DEG)

Electron in a material is attracted to the ions and feels repulsive force from any other electrons. As the result, in many-electron system there will be a spatial variation of the charge or known also as screening. One common example is electron will attract positive charged particles and creates a surplus of positive charge surrounding it and screens its field. Therefore we write the total charge density as a sum of the external (initial) and the induced charge density.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(\vec{r}) = \rho_{ext}(\vec{r}) + \rho_{ind}(\vec{r}) \!}

From the theory of the dielectric media, the external potential is assumed to be linearly related to the total physical potential

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi^{ext}(\vec{r}) = \int dr' \epsilon(\vec{r} - \vec{r'}) \phi(\vec{r'}) \!}

By using the Fourier transformation we can write this in the k-space as

Figure 2. Lindhard response function of 1DEG

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi^{ext}(\vec{q}) = \epsilon(\vec{q}) \phi(\vec{q}) \!}

And the induced charge density satisfies the relation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^{ind}(\vec{q}) = \chi(\vec{q}) \phi(\vec{q}) \!}

By using the perturbation theory and assuming linear response only, we get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi(\vec{q}) = -e^2 \int \frac{d^D k}{(2\pi)^D} \frac{f_{\vec{k}} - f_{\vec{k+q}}}{\epsilon_{\vec{k}}-\epsilon_{\vec{k}+\vec{q}}} \!}

Now consider T = 0 (Lindhard response function), we see that the integrand does not vanish only when either Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{\vec{k}} < \epsilon_F \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{\vec k + \vec q} > \epsilon_F \!} (or to say that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{\vec{k}} = 1 \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{\vec k + \vec q} = 0} ) or the opposite. What it means is the nonvanishing value comes from the electron-hole pairs (occupied-unoccupied states).

Now by evaluating the integral (for 1D case)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi(q) = -\frac{e^2}{2\pi} \int_{-k_F}^{k_F} dk \frac{1}{\frac{-\hbar^2}{2m} (2kq +q^2)} \!}

The resulting prefactor is not that important, we are interested in the q dependence of the result, which is.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi(q) \propto ln\left|\frac{q+2k_F}{q-2k_F}\right| \!}

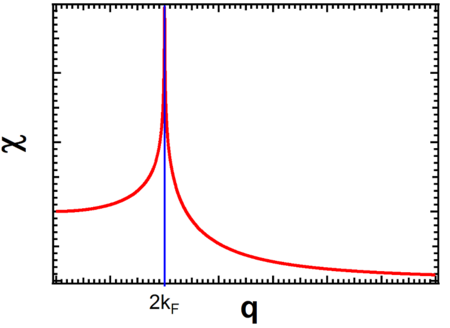
So, we see that the response function for 1DEG diverges at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = 2k_F \!} , what it means is that an external perturbation creates a divergent charge redistribution. By self consistency, at T = 0 the 1DEG is unstable with respect to the formation of a periodically varying electron charge or spin density. The period is related to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F \!} by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_0 = \pi / k_F \!} .

Nesting of the Fermi Surface

The divergence arises only in low-dimensional cases, this is due to a particular topology of the Fermi surface. In 2D case, the dispersion relation can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k}) = \epsilon_0 + 2t_a cos(k_x a) + 2t_b cos(k_y b) \!}

Where a and b are the lattice constants in the x and y direction and t's are the transfer integrals along those directions. For the case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_a >> t_b \!} (quasi 1D case), expanding the dispersion relation close to the Fermi surface yields

Figure 3. Fermi surface of a quasi-1D electron gas with a nesting vector Q

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k}) = \epsilon_0 + v_F (k_x - k_F) + 2t_b cos(k_y b) \! }

With this, the Fermi surface being the surface of a constant energy satisfies the condition

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_x = k_F - \frac{2t_b cos(k_y b)}{v_F} \!}

which leads to the sinusoidal Fermi surface in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_x - k_y \!} plane

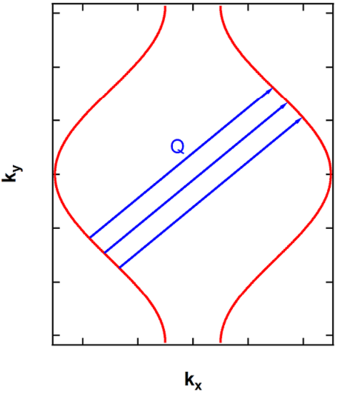
and we get a large number of electron-like pairs with similar energies, the condition for this particular case is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{Q} = (2k_F, \pi / b) \!}

Looking at the picture above, we see that each part of the Fermi surface can be translated perfectly into another using a particular vector, the same way as translating a unit cell of a crystal. The result is there is a large number of the overlapping of the Fermi surface. Fermi surface which has this kind of properties is said to exhibit a nesting. In 1D case, the Fermi surface is perfectly flat, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = 2k_F \!} gives the nesting condition and the number of the pair of states which satisfies this condition blows up.

Transition Temperature to Instabilities in 1DEG

Looking back at the equation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi(\vec{q}) \!} and evaluating near Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = 2k_F \!} at a finite temperature gives

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi(q=2k_F, T) = -e^2 n(\epsilon_F) ln \left(\frac{1.14 \epsilon_0}{k_B T}\right) \!}

With this, consider an external potential which induces a charge density which in turn creates an induced potential. Assuming linear relation between the induced density and the potential

$\phi ^{ind}({\vec {q}})=-g\rho ^{ind}({\vec {q}})\!$,

where g is just a constant, independent of q which indicates the how large induced potential produced by the induced charge is, then using the linear relation between the total potential and the induced charge

$\rho ^{ind}({\vec {q}})=\chi ({\vec {q}},T)\phi ({\vec {q}})\!$,

we can write the relation between the induced charge and the external potential only.

${\begin{aligned}\rho ^{ind}&=\chi ({\vec {q}},T)(\phi ^{ext}({\vec {q}})+\phi ^{ind}({\vec {q}})\\&=\chi ({\vec {q}},T)(\phi ^{ext}({\vec {q}})-g\rho ^{ind}({\vec {q}}))\\\end{aligned}}$

Grouping the induced charge density together, we obtain the relation

$\rho ^{ind}({\vec {q}})={\frac {\chi ({\vec {q}},T)\phi ^{ext}({\vec {q}})}{1+g\chi ({\vec {q}},T)}}\!$,

whose divergence happens when the denominator vanishes. This condition and substituting the susceptibility at a finite temperature gives

$1+gn(\epsilon _{F})ln{\frac {1.14\epsilon _{0}}{k_{B}T_{MF}}}=0\!$ with all factor absorbed into g. subscript MF is to indicate that the transition temperature is given by the mean field approach.

$T_{MF}={\frac {1.14\epsilon _{0}}{k_{B}}}exp\left({\frac {-1}{gn(\epsilon _{F})}}\right)\!$

Transition to the CDW

So far we considered only the electron, neglecting any interaction with the ions. However it appears that the lattice contributions cannot be neglected, not only that the electron interacts with the ions, but in 1D case the lattice is easily distorted. In this part, we shall consider a coupled electron-phonon system in 1D, the electron being 1DEG while the ions form a linear chain (remember the dehydrogenated polyethylene). This interaction is considered to depend only on the distance from the center of the ion, which is known also as the rigid ion approximation.

Using the second quantization scheme, we write the Hamiltonian for the free electron as

${\mathcal {H}}_{el}=\sum _{k}\epsilon _{k}a_{k}^{\dagger }a_{k}\!$,

and for the phonons

${\mathcal {H}}_{ph}=\sum _{q}\hbar \omega _{q}(b_{q}^{\dagger }b_{q}+1/2)\!$

The normal coordinates and conjugate momenta are given by the equations

$Q_{q}=\left({\frac {\hbar }{2M\omega _{q}}}\right)^{1/2}(b_{q}+b_{-q}^{\dagger })\qquad P_{q}=\left({\frac {\hbar M\omega _{q}}{2}}\right)^{1/2}(b_{q}^{\dagger }-b_{-q})\!$

With this, we write the lattice displacement as

$u(x)=\sum _{q}\left({\frac {\hbar }{2NM\omega _{q}}}\right)^{1/2}(b_{q}+b_{-q}^{\dagger })e^{iqx}\!$

where N is the number of lattice sites per unit length.

The total Hamiltonian with the interaction is also known as Frohlich Hamiltionian which is given by

INSERT STEPS? YES

${\mathcal {H}}=\sum _{k}\epsilon _{k}a_{k}^{\dagger }a_{k}+\sum _{q}\hbar \omega _{q}b_{q}^{\dagger }b_{q}+\sum _{k,q}g_{q}a_{k+q}^{\dagger }a_{k}(b_{-q}^{\dagger }+b_{q})\!$

with $g_{q}=i\left({\frac {\hbar }{2M\omega _{q}}}\right)^{1/2}|q|V_{q}\!$

as the electron-phonon coupling constant (previously when discussing only the electronic part we had g, but for an unspecified interaction, this one is different). With this Hamiltonian, the dynamics of the lattice vibration can be found by using

${\begin{aligned}{\dot {Q_{q}}}&={\frac {1}{i\hbar }}[Q_{q},{\mathcal {H}}]\\{\ddot {Q_{q}}}&=-{\frac {1}{\hbar ^{2}}}[[Q_{q},{\mathcal {H}}],{\mathcal {H}}],\!\end{aligned}}$

which gives a result ${\ddot {Q_{q}}}=-\omega _{q}^{2}Q_{q}-g_{q}\left({\frac {2\omega _{q}}{M\hbar }}\right)^{1/2}\rho _{q},\qquad \rho _{q}=\sum _{k}a_{k+q}^{\dagger }a_{k}\!$ is the q th part of the electronic density. Using the result for the electronic density that we obtained previously by considering the electronic contribution alone, the Hamiltonian becomes ${\ddot {Q_{q}}}=-\omega _{q}^{2}Q_{q}-g_{q}\left({\frac {2\omega _{q}}{M\hbar }}\right)^{1/2}\chi (q,T)V(q)\!$,

V is now the potential from the lattice. Looking back to our Hamiltonian, it is clear that this potential is given by

$V(q)=g_{q}(b_{-q}^{\dagger }+b_{q})=g_{q}\left({\frac {2M\omega _{q}}{\hbar }}\right)^{1/2}Q_{q}\!$

upon inserting V(q) into the equation a new frequency (renormalized frequency) is obtained

${\ddot {Q_{q}}}=-\underbrace {\left(\omega _{q}^{2}+{\frac {2g_{q}^{2}\chi (q,T)\omega _{q}}{\hbar }}\right)} _{\omega _{ren,q}^{2}}Q_{q}\!$

Therefore, the interaction part introduces a correction term to the lattice vibration frequency. Furthermore, we are interested only in $q=2k_{F}\!$ and the susceptibility at this q is known from before

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{ren, 2k_F}^2 = \omega_{2k_F}^2 - \frac{2g^2 n(\epsilon_F) \omega_{2k_F}}{\hbar} ln\left(\frac{1.14\epsilon_0}{k_B T}\right) \!}

The interesting part is when the renormalized frequency vanishes, it is known as "phonon softening" or basically a lattice distortion. This lattice distortion along with the electronic part leads to the formation of the CDW. The temperature at which they happen is easy to calculate

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{CDW}^{MF} = \frac{1.14 \epsilon_0}{k_B} exp\left(\frac{\hbar \omega_{2k_F}}{2g^2 n(\epsilon_F)}\right) \!}

CDW Order Parameter and Band Gap

The formation of the CDW as any other broken symmetry is associated with a nonzero order parameter. Based on what we have discussed so far, it makes sense to associate it with the lattice distortion that happens when the CDW is formed. For CDW it is complex and defined as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Delta|e^{i\phi} = g(\langle b_{2k_F} \rangle + \langle b^{\dagger}_{-2k_F} \rangle )\!} ,

and we rewrite our displacement operator in terms of the order parameter

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle u(x)\rangle &= \left(\frac{\hbar}{2NM\omega_{2k_F}}\right)^{1/2}\left[(\langle b_{2k_F} \rangle + \langle b^\dagger_{-2k_F}\rangle)e^{i2k_F x} + c. c.\right]\\ &= \left(\frac{\hbar}{2NM\omega_{2k_F}}\right)^{1/2}\left[ \frac{|\Delta|e^{i(2k_F x + \phi)}}{g} + \frac{|\Delta|e^{-i(2k_F x + \phi)}}{g}\right]\\ &= \left(\frac{\hbar}{2NM\omega_{2k_F}}\right)^{1/2}\frac{2|\Delta|}{g}cos(2k_F x + \phi)\\ &= \Delta u cos(2k_F x + \phi), \end{align} \!}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta u = \left(\frac{2\hbar}{NM\omega_{2k_F}}\right)^{1/2}\frac{|\Delta|}{g} \!} .

And by the method of mean field, we average out all of the phonon contribution in the Hamiltonian, viz.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = \sum_k \epsilon_k a^\dagger_k a_k + \sum_q \hbar \omega_q \langle b^\dagger_q b_q\rangle + \sum_{k,q}ga^\dagger_{k+q}a_k \langle b^\dagger_{-q} + b_q\rangle \!}

with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = \pm k_F} , by noting that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle b_{2k_F}\rangle = \langle b^\dagger_{-2k_F} \rangle \!} We are interested in the electronic part of this Hamiltonian. Well, in experiment we can see the charge ordering by using x-ray diffraction method (this method is actually indirect way to see it), but all peaks that appear are actually mainly scattered from the electron. Taking only the electronic part, noting that the third term at the r. h. s. can be written in term of the order parameter our Hamiltonian becomes:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_el = \sum_k \left[\epsilon_k a^\dagger_k a_k + |\Delta|e^{i\phi} a^\dagger_{k+2k_F}a_k + |\Delta|e^{-i\phi}a^\dagger_{k-2k_F}a_k\right]}

Now we move forward by considering only the states near the Fermi level. Now we change notation : index 1 and 2 denote the state near Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -k_F \!} respectively, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \!} is measured relative to the corresponding Fermi wave vector (therefore energy is also measured relative to the Fermi energy). We note that in the r. h. s of the equation above, there are creation and annihilation operators that correspond to the wave vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k - 2k_F \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k + 2k_F \!} . If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \!} happens to be near Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F \!} then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k + 2k_F \!} do not enter into our equation and the same for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k - 2k_F \!} if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!} is near Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -k_F \!} .

With the new notation, we write our Hamiltonian as follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = \sum_k \left[\epsilon_k (a^\dagger_{1,k}a_{1,k} - a^\dagger_{2,k} a_{2,k}) + |\Delta|e^{i\phi} a^\dagger_{1,k}a_{2,k} + |\Delta|e^{-i\phi} a^\dagger_{2,k}a_{1,k}\right] \!}

Now the Hamiltonian needs to be diagonalized. This can be done by introducing a canonical transformation (note that this transformation is similar to the kind of transformation in the BCS theory of superconductivity):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \gamma_{1,k} &= U_k e^{-i \phi /2}a_{1,k} - V_k e^{i \phi /2} a_{2,k}\\ \gamma_{2,k} &= V_k e^{-i\phi /2}a_{1,k} + U_k e^{i\phi /2} a_{2,k}, \end{align} \!}

with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_k^2 + V_k^2 = 1 \!}

What follows is just a simple algebra which results in a transformed Hamiltonian :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = \sum_k \left[\epsilon_k (U_k^2 - V_k^2) -2|\Delta|U_k V_k \right](\gamma^\dagger_{1,k} \gamma_{1,k} - \gamma^\dagger_{2,k} \gamma_{2,k}) + \left[2\epsilon_k U_k V_k + |\Delta| (U_k^2 - V_k^2)\right](\gamma^\dagger_{1,k} \gamma_{2,k} + \gamma^\dagger_{2,k} \gamma_{1,k}) \!} .

And it is clear that the Hamiltonian will be diagonalized provided the cross term vanishes. Therefore we proceed by requiring :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\epsilon_k U_k V_k + |\Delta|(U_k^2 - V_k^2) = 0 \!} .

To satisfy the constraint given above, we choose:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_k = cos\left(\frac{\theta_k}{2}\right) \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_k = sin\left(\frac{\theta_k}{2}\right)\!} .

With this choice upon zeroing the cross term, we will get:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\epsilon_k sin\left(\frac{\theta_k}{2}\right)cos\left(\frac{\theta_k}{2}\right) + |\Delta|\left(cos^2\left(\frac{\theta_k}{2}\right)- sin^2\left(\frac{\theta_k}{2}\right)\right) = 0 \!}

which is just Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle tan (\theta_k) = -\frac{|\Delta|}{\epsilon_k}} .

Now, knowing this we can use trigonometric relation to find what Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_k \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_k \!} are in terms of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Delta| \!} and $\epsilon _{k}\!$. Note the negative sign in the equation above, it means that either sine or cosine function will carry the sign. We choose

$cos(\theta _{k})=-{\frac {\epsilon _{k}}{\sqrt {\epsilon _{k}^{2}+|\Delta |^{2}}}}$ and $sin(\theta _{k})={\frac {|\Delta |}{\sqrt {\epsilon _{k}^{2}+|\Delta |^{2}}}}\!$ And again, use the trionometric relation :

$U_{k}={\frac {1}{2}}\left(1-{\frac {\epsilon _{k}}{E_{k}}}\right)\qquad V_{k}={\frac {1}{2}}\left(1+{\frac {\epsilon _{k}}{E_{k}}}\right)\!$

The next step is to substitute U and V into the Hamiltonian which gives :

${\mathcal {H}}=-\sum _{k}E_{k}(\gamma _{1,k}^{\dagger }\gamma _{1,k}-\gamma _{2,k}^{\dagger }\gamma _{2,k})\!$.

Based on the previous notation, all energies are relative to the Fermi energy, so we have to be careful when evaluating the absolute energy.

$\epsilon _{k}=\pm \hbar v_{F}(k-kF)\!$

However, it is more correct to be written as follows when evaluating $E_{k}\!$

$\epsilon _{k}=sgn(k-k_{F})\hbar v_{F}(k-k_{F}\!)$,

so we have

$E_{k}=sgn(k-k_{F})\left[\hbar ^{2}v_{F}^{2}(k-k_{F})^{2}+\Delta ^{2}\right]^{1/2}\!$

Or, if we wish to write it in total energy, not relative energy we can just add $\epsilon _{F}\!$ to the r. h. s.

Now we evaluate the phonon contribution to the energy which is $\sum _{q}\hbar \omega _{q}\langle b_{q}^{\dagger }b_{q}\rangle \!$, this is evaluated by the mean field scheme and gives, at $q=2k_{F}\!$

Figure 4 Dispersion relation near Fermi wave vector for pure 1DEG (blue) and for 1DEG with interaction with phonon (red)

${\begin{aligned}E_{ph}&=2\hbar \omega _{2k_{F}}\langle b_{2k_{F}}\rangle ^{2}\\&={\frac {\hbar \omega _{2k_{F}}|\Delta |^{2}}{2g^{2}}}.\end{aligned}}\!$

Therefore, we write the total Hamiltonian of the system as

${\mathcal {H}}=-\sum _{k}E_{k}(\gamma _{1,k}^{\dagger }\gamma _{1,k}-\gamma _{2,k}^{\dagger }\gamma _{2,k})+{\frac {\hbar \omega _{2k_{F}}\Delta ^{2}}{2g^{2}}}$,

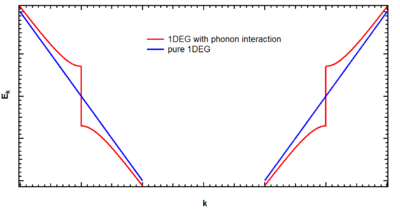
which is different from our previous dispersion relation because we obtain a band gap at $\pm k_{F}\!$ as we can see in figure 4. The next question will be whether or not the band gap opening leads to energy decrease or increase. It turns out that energy is lowered as can be proved by calculating the total energy of the electronic part.

${\begin{aligned}E_{el}&=n(\epsilon _{F})\int _{0}^{\epsilon _{F}}\left(\epsilon -(\epsilon ^{2}+\Delta ^{2})^{1/2}\right)\\&={\frac {n(\epsilon _{F})}{2}}\left[\epsilon _{F}^{2}-\left(\epsilon _{F}(\epsilon _{F}^{2}+\Delta ^{2})^{1/2}+\Delta ^{2}log{\frac {\epsilon _{F}+(\epsilon _{F}^{2}-\Delta ^{2})^{1/2}}{\Delta }}\right)\right]\end{aligned}}\!$

And considering weak coupling limit in which $\epsilon _{F}>>\Delta \!$, we will obtain

$E_{el}=n(\epsilon _{F})\left[-{\frac {\Delta ^{2}}{2}}-\Delta ^{2}log\left({\frac {2\epsilon _{F}}{\Delta }}\right)\right]+{\mathcal {O}}\left({\frac {\Delta }{\epsilon _{F}}}\right)\!$

On the other hand, lattice distortion leads to an increase in energy. Therefore, the stability is determined by whether or not the decrease in electronic part is greater than the increase in the lattice's elastic energy. The energy if the lattice is given by

$E_{latt}={\frac {\hbar \omega _{2k_{F}}\Delta ^{2}}{2g^{2}}}={\frac {\Delta ^{2}n(\epsilon _{F})}{2\lambda }}\!$

The total energy is

$E_{tot}=E_{el}+E_{latt}=n(\epsilon _{F})\left[-{\frac {\Delta ^{2}}{2}}-\Delta ^{2}log\left({\frac {2\epsilon _{F}}{\Delta }}\right)+{\frac {\Delta ^{2}}{2\lambda }}\right]\!$

The minimization of the total energy gives the gap size,

$\Delta =2\epsilon _{F}e^{1/\lambda }\!$

More calculation gives the difference in energy between the normal state and the CDW state which is the condensation energy :

$E_{con}=E_{normal}-E_{CDW}={\frac {n(\epsilon _{F})}{2}}\Delta ^{2}\!$,

which is definite positive and indicates that the CDW state has a lower energy than the normal one.

Upon comparing with our previous finding $K_{B}T_{CDW}^{MF}=1.14\epsilon _{0}e^{-1/\lambda }\!$, we get the gap size in terms of the CDW transition temperature, which is

$\Delta =1.76k_{B}T_{CDW}^{MF}\!$

This result is similar to the BCS relation for zero temperature gap and transition temperature.

Spatial Modulation

Based on the BCS theory, the ground state wave function is defined as

$\left|\phi _{0}\right\rangle \ =\left(\prod _{|k|<k_{F}}\gamma _{1,k}^{\dagger }\gamma _{2,k}^{\dagger }\right)|0\rangle \!$

And with our transformation, we can write this as

$|\phi _{o}\rangle =\prod _{|k|<k_{F}}\left(U_{k}e^{i\phi /2}a_{1,k}^{\dagger }-V_{k}e^{-i\phi /2}a_{2,k}^{\dagger }\right)\left(V_{k}e^{i\phi /2}a_{1,k}^{\dagger }+U_{k}e^{-i\phi /2}a_{2,k}^{\dagger }\right)|0\rangle \!$

The electronic density is defined as:

$\rho (x)=\langle \phi _{0}|\Psi ^{*}(x)\Psi (x)|\phi _{0}\rangle \!$,

with $\Psi (x)=\sum _{k}(a_{1,k}e^{ikx}+a_{2,k}e^{-ikx}).\!$

Noting that the expectation value for cross terms will vanish when the density operator is sandwiched between the ground state, we will get

$\rho (x)=\sum _{k}\left[U_{k}^{2}+V_{k}^{2}-U_{k}V_{k}e^{i(2kx+\phi )}-V_{k}U_{k}e^{-i(2kx+\phi )}\right]\!$,

which when integrated over all occupied states will give

$\rho (x)=\rho _{0}\left[1+{\frac {\Delta }{\hbar v_{F}k_{F}\lambda }}cos(2k_{F}x+\phi )\right]\!$

References

[1] R. E. Thorne, Charge-density wave conductors, Physics Today (May 1996)

[2] G. Gruner, Density waves in solids, Perseus Publishing (1994) (Main textbook, all discussions here are mostly following this book)

[3] H. Frohlich, On the thery of superconductivity : the one dimensional case, Proc. Roy. Soc A223, 296 (1954)

[4] R. E. Peierls, Quantum theory of soilds, Oxford University Press (1955)

[5] G. Gruner, The dynamics of charge-density waves, Rev. Mod. Phys. 60, 1129 (1988)

[6] S. Roth and D. Carroll, One-dimensional metals, Wiley-VCH (2004)

[7] S. Kagoshima, H. Nagasawa, and T. Sambongi, One-dimensional conductors, Springer (1988)