PHY6937

Welcome to Phy 6937 Superconductivity and superfluidity

PHY6937 is a one semester advanced graduate level course. Its aim is to introduce concepts and theoretical techniques for the description of superconductors and superfluids. This course is a natural continuation of the "many-body" course PHY5670 and will build on the logical framework introduced therein, i.e. broken symmetry and adiabatic continuity. The course will cover a range of topics, such as the connection between the phenomenological Ginzburg-Landau and the microscpic BCS theory, Migdal-Eliashberg treatment of phonon mediated superconductivity, unconventional superconductivity, superfluidity in He-4 and He-3, and Kosterlitz-Thouless theory of two dimensional superfluids.

The key component of the course is the collaborative student contribution to the course Wiki-textbook. Each team of students is responsible for BOTH writing the assigned chapter AND editing chapters of others.

Team assignments: Spring 2011 student teams

---

Outline of the course:

Pairing Hamiltonian and BCS instability

We can write the Hamiltonian of the system as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_\vec{r}[\psi_\sigma^\dagger (\vec{r})(\epsilon_\vec{p}-\mu)\psi_\sigma^\dagger (\vec{r}) +g\psi_\uparrow^\dagger (\vec{r})\psi_\downarrow^\dagger (\vec{r})\psi_\downarrow (\vec{r})\psi_\uparrow (\vec{r})]}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ g<0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ |g|<<\epsilon_{F}} .

For this system, the partition function is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D[\psi_\sigma ^{*} (\tau, \vec{r}), \psi_\sigma (\tau, \vec{r})]e^{-S_{BCS}}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{BCS}=\int_0^\beta d\tau \sum_\vec{r}[\psi_\sigma^\dagger (\tau, \vec{r})(\partial _\tau+\epsilon_\vec{p}-\mu)\psi_\sigma^\dagger (\vec{r}) +g\psi_\uparrow^\dagger (\vec{r})\psi_\downarrow^\dagger (\vec{r})\psi_\downarrow (\vec{r})\psi_\uparrow (\vec{r})]}

It doesn't matter to multiply partition function by a constant:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\rightarrow Z=\int D[\psi_\sigma ^{*} (\tau, \vec{r}), \psi_\sigma (\tau, \vec{r})] D[\Delta^{*}(\tau, \vec{r}),\Delta (\tau, \vec{r})] e^{-S_{BCS}-S_{\Delta}}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_\Delta=-\int_0^\beta d\tau\sum_{\vec{r}}\frac{1}{g}\Delta^*(\tau,\vec{r})\Delta(\tau,\vec{r})}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi^\dagger} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \psi} are grassmann numbers. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Delta^*} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Delta} are constant. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_\uparrow\psi_\downarrow} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_\downarrow\psi_\uparrow} behave like constant.

Let's make a shift of the constant:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \rightarrow \Delta+g\psi_\uparrow\psi_\downarrow}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta^*\rightarrow \Delta^*+g\psi^\dagger_\downarrow\psi^\dagger_\uparrow}

Then, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_\Delta=-\int_0^\beta d\tau \sum_{\vec{r}}{\{\frac{1}{g}\Delta^*\Delta + \Delta^*\psi_\uparrow \psi_\downarrow \Delta\psi^\dagger_\downarrow \psi^\dagger_\uparrow+g\psi^\dagger_\downarrow \psi^\dagger_\uparrow \psi_\uparrow \psi_\downarrow}\}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}S=&S_{BCS}+S_{\Delta}\\ =&\int_0^\beta d\tau \sum_{\vec{r}}\{ \psi_\sigma^\dagger(\tau, \vec{r})(\partial _\tau+\epsilon_\vec{p}-\mu)\psi_\sigma^\dagger (\tau, \vec{r}) \ \ \ \ \ \ \ \ \ \ \rightarrow S_0 \\ &+\Delta^*(\tau, \vec{r})\psi_\uparrow (\tau, \vec{r})\psi_\downarrow (\tau, \vec{r}) \Delta (\tau, \vec{r})\psi^\dagger_\downarrow (\tau, \vec{r})\psi^\dagger_\uparrow (\tau, \vec{r}) \rightarrow S_{int}\\ &-\frac{1}{g}\Delta^* (\tau, \vec{r})\Delta (\tau, \vec{r}) \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \rightarrow S_{\Delta} \end{align}}

then, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D[\psi_{\sigma}^{*}(\tau,\mathbf{r}),\psi_{\sigma}(\tau,\mathbf{r})]D[\Delta^{*}(\tau,\mathbf{r}),\Delta(\tau,\mathbf{r})]e^{-(S_{0}+S_{int.}+S_{\Delta})}} .

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle e^{-S_{int.}}\right\rangle _{0}\cong exp[\frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}+\frac{1}{4!}(\left\langle S_{int.}^{4}\right\rangle _{0}-3\left\langle S_{int.}^{2}\right\rangle _{0}^{2})]} by cumulant expansion, which guarantees that until the 2nd order, it is accurate.

Use Matsubara's Method

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{\sigma}(\tau,\mathbf{r})=\frac{1}{\beta}\underset{\omega_{n}}{\sum}\underset{\mathbf{k}}{\sum}e^{i\mathbf{k}\cdot\mathbf{r}}e^{-i\omega_{n}\tau}\psi_{\sigma}(i\omega_{n},\mathbf{k}), \omega_{n}=(2n+1)\frac{\pi}{\beta};}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta(\tau,\mathbf{r})=\frac{1}{\beta}\underset{\Omega_{n}}{\sum}\underset{\mathbf{k}}{\sum}e^{i\mathbf{k}\cdot\mathbf{r}}e^{-i\Omega_{n}\tau}\Delta_{\mathbf{k}}(i\Omega_{n}), \omega_{n}=2n\frac{\pi}{\beta}.}

Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{0}=\frac{L^{D}}{\beta}\underset{\omega_{n}}{\sum}\underset{\mathbf{k}}{\sum}[-i\omega_{n}+\varepsilon_{\mathbf{k}}-\mu]\psi_{\sigma}^{\dagger}(i\omega_{n},\mathbf{k})\psi_{\sigma}(i\omega_{n},\mathbf{k}).}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{int.}=\frac{L^{D}}{\beta^{2}}\underset{\omega_{n},\Omega_{n}}{\sum}\underset{\mathbf{k},\mathbf{q}}{\sum}[\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\psi_{\uparrow}(i\Omega_{n}-i\omega_{n},\mathbf{\mathbf{q}-k})\psi_{\downarrow}(i\omega_{n},\mathbf{k})+\Delta_{\mathbf{q}}(i\Omega_{n})\psi_{\downarrow}^{\dagger}(i\omega_{n},\mathbf{k})\psi_{\uparrow}^{\dagger}(i\Omega_{n}-i\omega_{n},\mathbf{\mathbf{q}-k})].}

The Fourier transform of 1 body Green's function is (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=1,2} mean Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbf{r}_{i},\tau_{i}}} ) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(1-2)=\left\langle \psi(1)\psi^{*}(2)\right\rangle =\frac{1}{\beta}\underset{\omega_{n}}{\sum}\frac{1}{L^{D}}\underset{\mathbf{k}}{\sum}e^{-i\omega_{n}(\tau_{1}-\tau_{2})}e^{i\mathbf{k}\cdot(\mathbf{r}_{1}-\mathbf{r}_{2})}\frac{1}{-i\omega_{n}+\varepsilon_{\mathbf{k}}-\mu}} ,

so Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\sigma}^{0}(i\omega_{n},\mathbf{k})=\left\langle \psi_{\sigma}(i\omega_{n},\mathbf{k})\psi_{\sigma}^{\dagger}(i\omega_{n},\mathbf{k})\right\rangle _{0}=\frac{\beta}{L^{D}}\frac{1}{-i\omega_{n}+\varepsilon_{\mathbf{k}}-\mu}} .

Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle S_{int.}^{2}\right\rangle _{0}=\frac{2L^{2D}}{\beta^{4}}\underset{\omega_{n},\Omega_{n}}{\sum}\underset{\mathbf{k},\mathbf{q}}{\sum}[G_{\uparrow}^{0}(i\omega_{n},\mathbf{k})G_{\downarrow}^{0}(i\Omega_{n}-i\omega_{n},\mathbf{q}-\mathbf{k})]\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})=L^{D}\frac{2}{\beta}\underset{\Omega_{n},\mathbf{q}}{\sum}\chi_{p}(\mathbf{q},i\Omega_{n})\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})} ,

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{p}(\mathbf{q},i\Omega_{n})=\frac{L^{D}}{\beta^{3}}\underset{\omega_{n},\mathbf{k}}{\sum}G_{\uparrow}^{0}(i\omega_{n},\mathbf{k})G_{\downarrow}^{0}(i\Omega_{n}-i\omega_{n},\mathbf{q}-\mathbf{k})} is called pairing susceptibility.

Let's calculate it:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{p}(\mathbf{q},i\Omega_{n})=\frac{L^{D}}{\beta^{3}}\underset{\omega_{n},\mathbf{k}}{\sum}G_{\uparrow}^{0}(i\omega_{n},\mathbf{k})G_{\downarrow}^{0}(i\Omega_{n}-i\omega_{n},\mathbf{q}-\mathbf{k})=\frac{1}{L^{D}}\frac{1}{\beta}\underset{\omega_{n},\mathbf{k}}{\sum}\frac{-1}{i\omega_{n}-\varepsilon_{\mathbf{k}}+\mu}\times\frac{1}{i\omega_{n}-i\Omega_{n}+\varepsilon_{\mathbf{q}-\mathbf{k}}-\mu}} ,

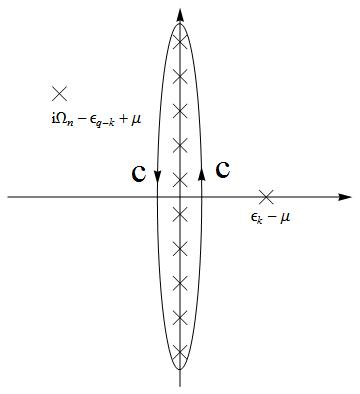
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow=\frac{1}{L^{D}}\frac{1}{\beta}\underset{\mathbf{k}}{\sum}\oint_{c}\frac{dz}{2\pi i}\frac{-1}{z-\varepsilon_{\mathbf{k}}+\mu}\times\frac{1}{z-i\Omega_{n}+\varepsilon_{\mathbf{q}-\mathbf{k}}-\mu}\frac{1}{e^{\beta z}+1}} .

Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-1}{z-\varepsilon_{\mathbf{k}}+\mu}\times\frac{1}{z-i\Omega_{n}+\varepsilon_{\mathbf{q}-\mathbf{k}}-\mu}=\frac{1}{\varepsilon_{\mathbf{q}-\mathbf{k}}+\varepsilon_{\mathbf{k}}-2\mu-i\Omega_{n}}[\frac{1}{z-\varepsilon_{\mathbf{q}}+\mu}-\frac{1}{z-i\Omega_{n}+\varepsilon_{\mathbf{q}-\mathbf{k}}-\mu}]} ,

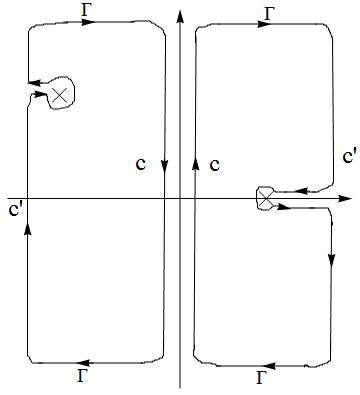
and change the integral path to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow=-\frac{1}{L^{D}}\frac{1}{\beta}\underset{\mathbf{k}}{\sum}\frac{1}{\varepsilon_{\mathbf{q}-\mathbf{k}}+\varepsilon_{\mathbf{k}}-2\mu-i\Omega_{n}}[\frac{1}{e^{\beta(\varepsilon_{\mathbf{q}}-\mu)}+1}-\frac{1}{e^{\beta(-\varepsilon_{\mathbf{q}-\mathbf{k}}+\mu)}+1}]=\int\frac{d^{D}k}{(2\pi)^{D}}\frac{1}{\varepsilon_{\mathbf{q}}+\varepsilon_{\mathbf{q}-\mathbf{k}}-2\mu-i\Omega_{n}}[1-f(\varepsilon_{\mathbf{k}})-f(\varepsilon_{\mathbf{q}-\mathbf{k}})].}

In the static (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Omega_{n}=0} ) and uniform (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{q}=0} ) limit,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-2f(\varepsilon_{\mathbf{k}})=Tanh[\frac{\beta}{2}(\varepsilon_{\mathbf{k}}-\mu)]} .

Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{p}(0,0)=\int\frac{d^{D}k}{(2\pi)^{D}}\frac{Tanh[\frac{\beta}{2}(\varepsilon_{\mathbf{k}}-\mu)]}{2(\varepsilon_{\mathbf{k}}-\mu)}} .

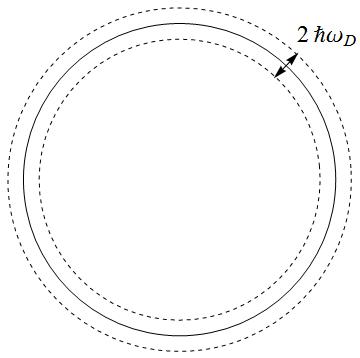
In low energy, integrate the energy in the shell near Fermi energy:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow\chi_{p}(0,0)\cong N(0)\int_{\hbar\omega_{D}}^{-\hbar\omega_{D}}d\xi\frac{Tanh[\xi\beta/2]}{2\xi}\cong N(0)\int_{0}^{-\hbar\omega_{D}}d\xi\frac{Tanh[\xi\beta/2]}{\xi}=N(0)ln[\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T}].}

Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}=L^{D}\frac{1}{\beta}\chi_{p}(0,0)\underset{\Omega_{n},\mathbf{q}}{\sum}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})} .

If we ignore the higher order in the cumulant expansion,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{eff}=-\underset{\mathbf{r}}{\sum}\int_{0}^{\beta}d\tau\frac{1}{g}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})-\frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}=\underset{\mathbf{r}}{\sum}\int_{0}^{\beta}d\tau[\frac{1}{\left|g\right|}-N(0)ln(\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T})]\Delta^{*}(\tau,\mathbf{r})\Delta(\tau,\mathbf{r})} .

Because the partition function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D\Delta^{*}D\Delta e^{-S_{eff}(\Delta)}} , if we only consider the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} related factors.

The superconductivity phase transition temperature is the temperature makes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\left|g\right|}-N(0)ln(\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T})=0} , which is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{c}=\frac{\hbar\omega_{D}}{k_{B}}\frac{2}{\pi}e^{\gamma}e^{-\frac{1}{N(0)\left|g\right|}}=1.134\frac{\hbar\omega_{D}}{k_{B}}e^{-\frac{1}{N(0)\left|g\right|}}} .

Beyond the critical temperature, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} related factors in the partition function is just Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} , the same as no cooper pair, which is normal state; below the critical temperature, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} related factors in the partition function will diverge, which means superconductivity phase transition.

Finite Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{q}} (small) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ (\Omega_n=0)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_p (q,0)-\chi_p (0,0)=\frac{1}{L^D} \sum_k \frac{1}{\beta} \sum_{i\omega_n}\frac{-1}{i\omega_n-\epsilon_k+\mu}(\frac{1}{i\omega_n+\epsilon_{q-k}-\mu}-\frac{1}{i\omega_n+\epsilon_{-k}-\mu}) }

for small ${\vec {q}}$, $\epsilon _{q-k}=\epsilon _{-k}+q{\frac {\partial \epsilon _{\rho }}{\partial \rho }}|_{\rho =-k}=\epsilon _{\vec {k}}+{\vec {q}}\cdot {\vec {v}}_{-k}=\epsilon _{k}-{\vec {q}}\cdot {\vec {v}}_{k}$

and ${\frac {1}{i\omega _{n}+\epsilon _{k}-\mu -q\cdot v_{k}}}={\frac {1}{i\omega _{n}+\epsilon _{k}-\mu }}+{\frac {q\cdot v_{k}}{(i\omega _{n}+\epsilon _{k}-\mu )^{2}}}+{\frac {(q\cdot v_{k})^{2}}{(i\omega _{n}+\epsilon _{k}-\mu )^{3}}}$

Thus,

${\begin{aligned}\chi _{p}(q,0)-\chi _{p}(0,0)&={\frac {1}{L^{D}}}\sum _{k}{\frac {1}{\beta }}\sum _{i\omega _{n}}{\frac {-1}{i\omega _{n}-\epsilon _{k}+\mu }}\left({\frac {q\cdot v_{k}}{(i\omega _{n}+\epsilon _{k}-\mu )^{2}}}+{\frac {(q\cdot v_{k})^{2}}{(i\omega _{n}+\epsilon _{k}-\mu )^{3}}}+...\right)\\&={\frac {-1}{\beta }}\sum _{i}\omega _{n}\int {\frac {d^{D}k}{(2\pi )^{D}}}{\frac {({\vec {q}}\cdot {\vec {v}}_{k})^{2}}{(i\omega _{n}-\epsilon _{k}+\mu )(i\omega _{n}+\epsilon _{k}-\mu )^{3}}}\end{aligned}}$

Consider the states near the $\hbar \omega _{D}$ shell near fermi surface, we have

$\chi _{p}(q,0)-\chi _{p}(0,0)={\frac {1}{\beta }}\sum _{i\omega _{n}}\int {\frac {d\Omega _{F.S.}}{\Omega _{D}}}(q\cdot v_{F})^{2}\int _{-\infty }^{+\infty }d\xi N(\xi +\mu ){\frac {1}{(\xi -i\omega _{n})(\xi +i\omega _{n})^{3}}}$

where, $\ \xi =\epsilon _{k}-\mu$

and

${\begin{aligned}\int _{-\infty }^{+\infty }d\xi {\frac {1}{(\xi -i\omega _{n})(\xi +i\omega _{n})^{3}}}&={\frac {2\pi i}{(2i\omega _{n})^{3}}}\theta (\omega _{n})-{\frac {2\pi i}{(2i\omega _{n})^{3}}}\theta (-\omega _{n})\\&={\frac {2\pi i}{(2i|\omega |)^{3}}}\end{aligned}}$

So,

${\begin{aligned}\chi _{p}(q,0)-\chi _{p}(0,0)&={\frac {1}{\beta }}\sum _{i\omega _{n}}N(0)\int {\frac {d\Omega }{\Omega _{D}}}(q\cdot v_{F})^{2}{\frac {2\pi i}{(2i|\omega |)^{3}}}\\&=N(0)v_{F}^{2}|{\vec {q}}|^{2}\int {\frac {d\Omega }{\Omega _{D}}}(q\cdot v_{F})^{2}{\frac {1}{\beta }}\sum _{i\omega }{\frac {2\pi i}{-i8|{\frac {(2n+1)\pi }{\beta }}|^{3}}}\\&=-{\frac {1}{4}}N(0)v_{F}^{2}q^{2}(<({\hat {q}}\cdot {\hat {v_{F}}})>_{F.S.}){\frac {\beta ^{2}}{\pi ^{2}}}(\sum _{N=-\infty }^{+\infty }{\frac {1}{|2n+1|^{3}}})\end{aligned}}$

$\sum _{N=-\infty }^{+\infty }{\frac {1}{|2n+1|^{3}}}=\sum _{n=0}^{\infty }{\frac {2}{(2n+1)^{3}}}={\frac {2}{\pi }}{\frac {7\zeta (3)}{8}}$

where, $\ \zeta (3)$ is Riemann zeta function.

$<({\hat {q}}\cdot {\hat {v}}_{F})^{2}>_{F.S.}={\frac {1}{D}}$

For spherical F.S. in 3D,

$\int {\frac {d\Omega }{\Omega _{D}}}({\hat {q}}\cdot {\hat {v}}_{F})^{2}={\frac {2\pi }{4\pi }}\int _{-1}^{1}dcos\theta cos^{2}\theta ={\frac {1}{3}}$

For circular F.S. in 2D,

$\int {\frac {d\Omega }{\Omega _{D}}}({\hat {q}}\cdot {\hat {v}}_{F})^{2}={\frac {1}{2\pi }}\int _{0}^{2\pi }d\theta cos^{2}\theta ={\frac {1}{2}}$

Then

${\begin{aligned}\chi _{p}(q,0)-\chi _{p}(0,0)&=-{\frac {1}{4}}N(0)v_{F}^{2}q^{2}{\frac {1}{D}}{\frac {\beta ^{2}}{\pi ^{2}}}{\frac {2}{\pi }}{\frac {7\zeta (3)}{8}}\\&=-N(0){\frac {7\zeta (3)}{16D\pi ^{2}}}q^{2}{\frac {1}{\pi \hbar ^{2}}}\left({\frac {\hbar v_{F}}{k_{B}T}}\right)^{2}\\&\equiv -N(0)q^{2}\xi ^{2}\end{aligned}}$

So

${\begin{aligned}{\frac {1}{2}}\left\langle S_{int.}^{2}\right\rangle _{0}&=L^{D}{\frac {1}{\beta }}{\underset {\Omega _{n},\mathbf {q} }{\sum }}\chi _{p}(q,0)\Delta _{\mathbf {q} }^{*}(i\Omega _{n})\Delta _{\mathbf {q} }(i\Omega _{n})\\&=N(0)ln[{\frac {2\hbar \omega _{D}e^{\gamma }}{\pi k_{B}T}}]L^{D}{\frac {1}{\beta }}{\underset {\Omega _{n},\mathbf {q} }{\sum }}\Delta _{\mathbf {q} }^{*}(i\Omega _{n})\Delta _{\mathbf {q} }(i\Omega _{n})-L^{D}{\frac {1}{\beta }}{\underset {\Omega _{n},\mathbf {q} }{\sum }}N(0)q^{2}\xi ^{2}\Delta _{\mathbf {q} }^{*}(i\Omega _{n})\Delta _{\mathbf {q} }(i\Omega _{n})\end{aligned}}$.

$S_{eff}={\underset {\mathbf {r} }{\sum }}\int _{0}^{\beta }d\tau \left[\left({\frac {1}{\left|g\right|}}-N(0)ln({\frac {2\hbar \omega _{D}e^{\gamma }}{\pi k_{B}T}})\right)\Delta ^{*}(\tau ,\mathbf {r} )\Delta (\tau ,\mathbf {r} )-N(0)\xi ^{2}(\nabla \cdot \Delta ^{*}(\tau ,\mathbf {r} ))(\nabla \cdot \Delta (\tau ,\mathbf {r} ))\right]$.

Note that the last term in the expression tells us that $S_{eff}$ would increase if gradient of $\Delta$ is not zero.

Note that the above expression has a one-one correspondant to the Giznburg-Landau functional:

$F=\int d^{D}r\left[\alpha (T-T_{c})|\Psi (r)|^{2}+{\frac {\hbar ^{2}}{2m^{*}}}|\nabla \Psi |^{2}\right]$,

here the $\ \Delta$ in the previous expression corresponds to $\ \Psi$ in the G-L expression.

Observe that