Notes 1

Atomic Nuclei

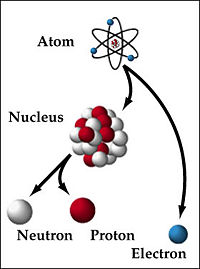
The atomic nucleus is quantum system composed of protons, neutron, and electrons who interact together to form a bound system. The forces acting on this system, strong force, weak force, the Coulomb force, and gravity, act on the system over various length scales that effect the overall distributions of the particle wavefunctions composing the nucleus. The strong force acts on length scales of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-15}} m and below, primarily affecting the quark components of the previously mentioned nucleons. The weak force acts on a scale of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-18}} m, acting on the range of the nucleons as it is the affect of boson exchange. The electric, i.e. Coulomb, force acting on the nuclei also acts at all ranges, modeling the interaction of the charged nucleon present in the system with one another. Finally, the gravitational force acts also acts at all ranges, and is the weakest of the four nuclear forces.

Within a given nucleus, denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle _Z^A X_N} , there are multiple levels of organizations. The protons and neutrons, closely bound by the nuclear forces, form a system whose energy levels are quantized, forming a shell structure hierarchy, for both the protons and neutron, whose energy levels often interact between one another. These nucleons are each composed of three individual particles known as quarks, bound together by the strong force.

The characteristics of the nuclides follow general trend lines based on both isomer, and isotope number, as seen by the nuclide chart posted here. A region of stability is observed, beyond which increases in proton or neutron number outside of the dripline (seen here in black) causes rapid decay of the nucleus in question.

Definitions for Abundances

To facilitate an understanding regarding the elements present in a given cosmological event or object, a framework must be established to properly measure the distribution of particles present. To this end, the nuclear abundance is presented as a measure of the number of a given isotope present in a quantity of measured element. This particle abundance is defined as follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_i = \frac{n_i}{\sum_{j} n_j} \ , }

where the sum is counted over all isotopes present in the data and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i} is the particle's number density. This is often set logarithmically and normalized to the amount of hydrogen present, creating what is known as the relative particle abundance:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_i = \log_{10} X_i + 12 \ , }

Furthermore, the mass fraction is defined to be the fraction of total mass of a sample that is composed of the particular nucleus in question, i.e.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_i = \frac{m_i}{m_{tot}} = \frac{m_i n_i}{\rho} \approx \frac{A_i n_i}{\rho N_A} \ . }

Denoting the mass per baryon as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_i\equiv \frac{X_i}{A_i} \ , }

the particles number density can be defined by this baryon fraction and the density of the sample

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i = Y_i \rho N_A \ . }

The mean molecular weight is determined by

Other important quantities for consideration would be the mean molecular weight, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_i = \frac{\sum_i{A_i Y_i}}{\sum_i Y_i} = \frac{\sum_i X_i }{\sum_i Y_i} = \frac{1}{\sum_i Y_i} \,} , the electron abundance,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_e = \sum_i Z_i Y_i \ ,} , and the electron number density, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_e = Y_e \rho N_A \ .}

Solar System Abundances

Solar abundances, i.e. the quantity of various species of nuclei present in the solar system, tell us a great deal about how the solar system was formed and provide insight into galactic evolution as a whole. To this end, the nature of studying solar abundances can be broken into three disciplines studying the various classes of data present.

Earth materials

To this end, various materials on earth are examined to see what sort of composition of elements were present during the formation of the solar system. The problem that is encountered, however, is the chemical fractionation strongly hinders this process, changing the apparent concentrations. Isotopic compositions, however, do not exhibit this feature however and are ideal candidates for study.

Solar Spectra

Since the sun formed directly from presolar nebula, examination of the spectra observed from its photosphere, i.e. non-fusion process layer, sheds light on the early composition of the solar system prior to structure formation.

Meteorites

Finally, meteorites found on earth, which have not been exposed to extreme temperatures and pressures that would cause the chemical fractionation seen in earthen materials, can be used to sample presolar nebula composition. These meteorites are broken into three classes, stones(93%), stony irons(1.5%), and irons(5.5%). Stones, which are subdivided into chondrites(86%) and achondrites(7%) are by far the largest in abundance, with the chondrites providing some of the best, unfractionated samples of presolar nuclear composition.

Quantum Mechanics

In the late 19th and early 20th centuries, new physical theories were stretching the limits of classical mechanics as well as classical theories of electricity and magnetism. Physicists needed new theoretical tools for describing quantum systems that would reduce to that of macroscopic systems at the proper boundaries.

The famed double slit experiment offered new, unexplained experimental data which led to the to the understanding of particle-wave duality. This is to say that any particle has wavelike properties and thus can be represented as a wave, and visa versa. This is one of the most important theories in all of quantum mechanics. This data was obtained by firing a beam of electrons through 2 slits, and instead of seeing a bright band on the detector screen an interference pattern, similar to that of light waves, was observed.

Another example of the limitations of classical mechanics is in regard to the stability of the atom. Classical theory would suggest that electrons orbiting a nucleus would lose energy by emitting photons and subsequently crash into the nucleus. Niels Bohr proposed an atomic model in which electrons had discrete energy levels. This theory of quantized energy states was the foundation for modern day quantum mechanics. Once experimental data confirming this theory, or a theory similar, was obtained by James Franck and Gustav Hertz, research into quantum theory greatly increased.

The Schrödinger Equation

Possibly the most important equation in all of quantum mechanics is Schrödinger's wave equation. This partial differential equation represents the change of quantum states over time. The wavefunction represents the probability of a particular quantum state being occupied.

The most general form of the equation is as follows, where E is the energy operator, and H is the Hamiltonian operator.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\Psi = \hat H \Psi}

The equation can be rewritten in a time dependent form and a time independent form.

The time dependent equation: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \hbar{\partial \over \partial t} \Psi(x,\,t) = \hat H \Psi(x,\,t)}

The time independent equation: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {E}\psi(r) = - {\hbar^2 \over 2m} \nabla^2 \psi(r) + V(r) \psi(r)}

The time independent equation represents a situation in which the energy of the system is constant in time.

Thermodynamics

Thermodynamics is also essential to understanding Astrophysical processes. Thermodynamics, study of energy transport, dominate many Astrophysical processes most notably stars. For this reason included is a brief discussion of variables uses in thermodynamics and the primary equations, pressure, number density, particle density, state density, total number of states, and the equation of state and various other thermodynamic principles where they are needed.

Systems

To begin the discussion of thermodynamics we look at the concept of systems. A system is a region of space that is being studied, this region is defined as the space inside of the boundary. Everything outside of the boundary is known as the environment. The system can exchange energy, work and matter with the environment. There are also closed systems in which only heat and work can be transferred from the system to the environment or vice versa. In a closed system to matter can be exchanged.

Thermodynamical Variables

To begin, we look at the key variables that define a statistical system.

First we define entropy, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S\!} , as the energy of a system that is not available to do work. In general, entropy is defined as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = k_{b} \ln{\Omega}\!} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega\!} is the number of states in the system.

The internal energy of the system, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U\!} , is the energy necessary to create the system, defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dU = Tds - PdV + \sum_{i}\mu_{i}dN_{i}\!} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu\!} is the chemical potential.

The chemical potential, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu\!} , of a system is the change in a characteristic thermodynamic state function per change in the number of molecules.

The Helmholtz free energy, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\!} is a measure the work obtainable from a closed thermodynamic system at a constant temperature and volume, defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = U - TS\!} and the change in Helmholtz free energy as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dA = -TdS - PdV + \sum_{i}\mu_{i}dN_{i}\!} .

The Gibbs free energy of the system, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G\!} , measures the useful work obtained from the from an isothermal, isobaric system, and is defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G = U - TS + PV\!} , where the change in Gibbs free energy is said to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dG = dU - SdT + VdP\!} .

Heat, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q\!} , is defined to be the energy transferred between two thermodynamical systems via a thermal contact and is defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q = q V \!} with a change in heat given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dQ = T dS \!} .

Finally, enthalpy, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\!} , is defined as a measure of the total energy of a thermodynamical system, given by the expression Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = U + PV\!} and the change in enthalpy as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dH = TdS + PdV + \sum_{i}\mu_{i}dN_{i}\!} .

Thermodynamical Quantities

Now we move to discuss the various equations that define a thermodynamical system outside of its principle variables. Defining the occupational probability function as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p)\!} and the state density function as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega\!} , then we can express the following quantities in compact form:

Pressure

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{1}{3}\int^{\infty}_{0}pv\omega(p)f(p)dp }

Energy Density

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = \frac{U}{V} = \int^{\infty}_{0}E\omega(p)f(p)dp }

Particle Density

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \frac{N}{V} = \int^{\infty}_{0}\omega(p)f(p)dp }

State Density

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(E) = 2\pi\frac{g}{h^{3}}(2m)^{3/2}E^{1/2} }

Number of States

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(E) = \frac{4\pi}{3}\frac{g}{h^{3}}(2mE)^{3/2} }

Occupation Probability

Fermi-Dirac

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p) = \frac{1}{e^{(E(p)-\mu)/k_{b}T} + 1} }

Bose-Einstein

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p) = \frac{1}{e^{(E(p)-\mu)/k_{b}T} - 1} }

Maxwell-Boltzmann

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p) = {e^{-(E(p)-\mu)/k_{b}T}} }

Above, E(p) is the energy of the state, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} represents the chemical potential, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_b} is the Boltzmann constant, and T is the temperature.

A Simple Application

In stellar structures, the force of gravity acting on the stellar matter must balance with the outward pressure in order to avoid collapse or expansion.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial P_r}{\partial r}=-\rho_r \frac{Gm_r}{r^2}}

Nuclear Physics

Nuclear physics is the field of study pertaining to the interaction of atomic nuclei and the forces that act on them. The applications of nuclear physics range from nuclear defense, to power, to medical technologies and more as new improvements in the field open up new avenues of study.

Basic Ingredients

What one first has to discuss when talking about nuclear physics is what particles and forces are actually playing a roll, and how is their role satisfied in the system. When we talk about nuclear physics, in general, we're talking about the interactions of protons and neutrons inside of a nucleus and how they form together to yield various nuclei.

The forces that govern this interaction are the Strong nuclear force and the electromagnetic force. Due to the interaction with this electromagnetic force, it is possible to probe inside the atom to measure the relative size of the nucleus by use of electron scattering, where electrons are deflected away from the nucleus due to the presence of a Coulomb barrier created by the protons. Examination of the amount of electrons deflected at certain angles gives insight into the charge distribution of the nucleus, which surprisingly does not appear to be uniform. Instead, the charge distribution takes on an effective Woods-Saxon shape defined as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(r) = \frac{\rho_{0}}{1 + e^{\frac{r - R}{a_{v}}}}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R = 1.18\!} xFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{\frac{1}{3}} - 0.048 fm } and $a_{v}=0.055\pm 0.07fm$.

Another factor at play in the nucleus is the binding energy that holds it together, overcoming the Coulomb repulsion at extremely short range. In general, this energy can be related to the difference between the mass of the constituent particles and the actual mass of the system, therefore, letting $c=1$, the binding energy for a nucleus is approxiamtely$B(Z,N)=Zm_{p}+Nm_{n}-M(Z,N)\!$.

Models

In order to better represent the nucleus, models are often used which facilitate the examination of various nuclear phenomena. These models simply the problem and allow for comparison to observed data which dictate how well the model works in its effort to describe the nucleus.

Independent Particle Model

The Independent Particle Model, sometimes referred to as the Fermi model, treats the nucleus as a fermi gas in equilibrium in order to model the energy. It should be noted that this model is only technically correct in the limit of infinite nuclear charge. Here the binding energy can be calculated by use of the number of states, $\Phi \!$, and the fermi energy, $E_{F}\!$ of the nucleus.

Letting $E_{F}={\frac {h^{2}}{2m}}({\frac {3}{8\pi }}{\frac {N}{V}})^{2/3}$, we can define the mean binding energy as

$E_{mean}={\frac {1}{\Phi (E)}}\int _{0}^{E_{F}}EdE={\frac {3}{5}}E_{F}$.

Droplet Model

Since the density of a nucleus was experimentally seen to be roughly constant, the liquid drop model developed as a means of representing this and taking into account the fact that forces acting at the surface of the nucleus would in fact be different then those acting on the internal nucleons. The binding energy can therefore by established by creating a term proportional to the volume of the nucleus, and making corrections to it based on geometry and basic physics. To begin, the volume term, $a_{V}V\!$, must be modified by a correction term to account for the difference in forces on the surface and inside of the nucleus. This surface term is therefore proportional to the surface area of the nucleus, and is a negative to account for the effective over counting of the volume term, therefore given by $-a_{S}A^{\frac {2}{3}}\!$. Furthermore, another term must be added to account for the repulsion between protons, which pushes them apart and lowers the binding energy, therefore making the term negative. This Coulomb term would have to count all interactions of protons inside the nucleus, and therefore would be roughly proportional to $Z^{2}\!$, so that it can be defined as $-a_{C}{\frac {Z^{2}}{A^{\frac {1}{3}}}}\!$. Another term, the asymmetry term is added to account for uneven counts of neutrons and protons, leading to differences in shell energies that bide for control in the nucleus. By use of the fermi exclusion principle, this energy correction term can be written as $-a_{A}{\frac {(Z-{\frac {A}{2}})^{2}}{A}}\!$. A final term is added to account for the Cooper pair interactions for the nucleons, and is different for different types of nuclei. This Term, $B_{pair}(Z,N)\!$, is ${\frac {12}{\sqrt {A}}}\!$ for even-even nuclei, $0\!$ for odd A nuclei, and $-{\frac {12}{\sqrt {A}}}\!$ for odd-odd nuclei. We can then finally write the binding energy for the liquid drop model as

$B(Z,N)=a_{V}V-a_{S}A^{\frac {2}{3}}-a_{C}{\frac {Z^{2}}{A^{\frac {1}{3}}}}-a_{A}{\frac {(Z-{\frac {A}{2}})^{2}}{A}}+B_{pair}(Z,N)\!$

where experimental data can be used to give values for the constants, with $a_{V}=16MeV\!$, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{S} = 18.5 MeV\!} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_C = 0.72 MeV\!} , and $a_{A}=23.4MeV\!$.

Shell Model

One of the main problems with the liquid drop model is that it begins to fail at describing nuclei in any consistent manner in the region of very low Z. This this end, the shell model was introduced, effectively accounting for all nuclear interactions regardless of Z number. However, the shell model becomes increasingly complex the higher up in Z one goes, and correlations between neutron and proton shells have to be accounted for, as well as spin interactions which become a predominant factor in heavier nuclei. It is, however, a very effective way of modeling low Z nuclei and eliminates the discrepancies between theoretical and experimental data. This uses the Pauli exclusion principle to define the nucleus in terms of discrete energy levels. This leads to filled "shells" of the nucleus which correspond to certain "magic numbers" for nuclear number Z, corresponding to trends in experimental data where these particular nuclei deviated from trends of their neighbors. This is generally done by taking a harmonic oscillator potential and deforming it into a Woods-Saxon potential, which is very effective at modeling the nucleus, and the corresponding Schrodinger equations are solved, yielding all possible states of the nucleus.

Decays and Stability

Given the wide range of possible isotopes and isotopes and isotones that exist, it becomes important to establish which ones are stable, i.e. long-lived, and which ones have very short life times, leading to the decay of the nucleus into various particles. In order for a particle to decay, two conditions must be satisfied. First, it must loose energy in the process of the decay, so that it can be closer to a ground state, as nuclei do not like being in excited states. Second, a transition must actually exist, via decay chains of alpha and beta decay, that can actually lead to the production of said nucleus. We see, along the middle of the table of nuclides, a finite region of stability known as the nuclear drip line. The equations governing the size of this drip line map out both the isotope stability, i.e. neutron drip line, and the isotone stability, the proton drip line, and are given by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_n(Z,A) = M(Z,A - 1) + m_n - M(Z,A)\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_p(Z,A) = M(Z - 1,A - 1) + m_p - M(Z,A)\!}

Nuclear Reactions and Cross Sections

In order to properly study nuclear reactions, a framework must be presented that details the theoretical values in relation to quantities that are measurable in the lab. To this end, the formalism of both transmission coefficients and nuclear cross sections are discussed below

A basic nuclear reaction is written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(b,c)D \!}

where $A\!$ is the heavy target nucleus, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b\!} is the projective, that is the particle being accelerated at the target, $c\!$ is the lighter outgoing particle, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D\!} is the residual nucleus.

Decays and Transmission Coefficients

In general there are two kinds of reactions. Direct Reactions, where the target nucleus and projectile interact to form a bound state, where the new nucleus is stable. The other is a Resonant Reaction where after the target nucleus and projectile interact an unstable particle is formed that then decays to a stable state.

Transmission probabilities refer to the probability of a nucleus decaying from a state of higher potential to one of lower potential. Within the context of a particle beam and target, the transmission probability can be represented by relating the flux of incident particles to the transmitted particle flux. These values of flux can be elucidated by the quantum mechanical equation of flux, ${\vec {j}}$.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{j}=\frac{\hbar}{2mi} (\phi ^*\vec\bigtriangledown\phi - \phi\vec\bigtriangledown\phi^*)}

${\hat {T}}={\frac {j_{trans}}{j_{inc}}}$

Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{T} } is the transmission coefficient, which relates the intensity of the transmitted wave to that of the incident wave. This value becomes...

${\hat {T}}=4{\frac {{\frac {2m}{\hbar }}{\sqrt {(E+V_{0})E}}}{\left[{\sqrt {{\frac {2m}{\hbar }}(E+V_{0})}}+{\sqrt {{\frac {2m}{\hbar }}E}}\right]^{2}}}$

Applied to quantum mechanics, the transmission coefficient acts as a probability of quantum tunneling to occur.

Nuclear Cross Section

Formally, the nuclear cross section is defined to be the effective area of a nucleus for a given reaction channel. Implicitly, this means that the cross section, hereby refereed to as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma\!} , is not the actual cross sectional area of a hard sphere-type problem, but rather the area that an incoming particle or photon "sees", such that if the particles path takes it through this area, the particular reaction in study takes place. $\sigma \!$ is experimentally measured as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \frac{N_R / t}{\left [ N_b/(tA) \right ]N_t} }

Where $N_{R}/t\!$ is the number of interactions per time, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_b/(tA) \!} is the number of incident particles per area per time, and $N_{t}\!$ is the number of non-overlapping target nuclei within the beam.

Relative to the tunneling probability, i.e. the transmission coefficient discussed above, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma\!} can be defined, relative to angular momentum $l\!$ by the following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \frac{\pi}{k^2}\sum_{l=0}^{\infty}(2l + 1)T_l }

In order to properly define the cross section, the incoming flux as described by a plane wave, is needed, as well as the scattering as a function of angle and the penetration probability of the nucleus. Given an incoming plane wave described as

$\psi _{in}={\sqrt {4\pi }}\sum _{l=0}^{\infty }{\sqrt {2l+1}}i^{l}j_{l}(kr)Y_{l,0}(\theta )$,

a transmitted wave described as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{t} = \frac{\sqrt{\pi}}{kr}\sum_{l=0}^{\infty}\sqrt{2l + 1}i^{l+1}(e^{-i(kr - \frac{l\pi}{2})} - \eta_le^{i(kr - \frac{l\pi}{2})}Y_{l,0}(\theta) } ,

where $\eta _{l}\!$ relates to the penetration probability, and an expression for the scattering as a function of angle given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\int\vec{e_r}\vec{j_t}r^2d\Omega = -\frac{\hbar}{2im}\int(\psi^*_t\frac{\partial}{\partial r}\psi_t - \psi_t\frac{\partial}{\partial r}\psi^*_t)r^2d\Omega }

allows us to reach the following expression for $\sigma \!$:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \frac{-\int\vec{e_r}\vec{j_t}r^2d\Omega}{|\vec{j_{in}}|}}

where $|{\vec {j_{in}}}|={\frac {\hbar k}{m}}$.

From this quantity and the penetration probability and energy, a new variable is introduced known as the astrophysical S-factor, which plays a roll in identifying the type and scale of transitions seen from scattering:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(E) = \sigma E e^{2\pi\eta}\!} .

Thermonuclear Reactions

A thermonuclear reaction refers to the fusion of two light atomic nuclei into a single heavier nucleus by means of collision at extremely high temperatures, releasing a large amount of energy. These reactions can persist in chains, or cycles, that continue the nuclear evolution to higher Z nuclei. These cycles, such as proton-proton, and carbon, account for the majority of energy radiated by the Sun and most other stars in the universe.

Reaction Rates

The reaction rate is intuitively defined as how fast or slow a reaction takes place, and is key in understanding thermonuclear reactions and reaction chains. Relative to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma\!} , the reaction rate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!} is defined by the following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \frac{number\;of\;reactions\;target^{-1}sec^{-1}}{flux\;of\;incoming\;projectiles} = \frac{r/n_i}{n_jv} }

Therefore, in order to discuss the reaction rates properly, one needs to know both the cross section of the reaction and the velocity distribution of the beam and target. To begin, as a relative to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j\!} particle, the equation is rearranged to define the reaction rate relative to the integrated mean of the cross sections and velocities:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{i,j} = n_in_j \langle\sigma v\rangle_{i.j} }

This integrated mean is given, in terms of the phase space distributions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\vec{v}}\!} as the following: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{i,j} = n_in_j \int\sigma(|\vec{v}_i - \vec{v}_j|)|\vec{v}_i - \vec{v}_j|\phi(\vec{v}_i)\phi(\vec{v}_j)d^3v_id^3v_j } where the distribution functions are defined as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(\vec{v}_i)\phi(\vec{v}_j) = \frac{(m_im_j)^{3/2}}{(2\pi kT)^3}e^{-\frac{m_iv_i^2+m_jv_j^2}{2kT}}\!} .

The next step is to transform the integrated mean into the center of mass, using the substitions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M = m_i + m_j, \mu = \frac{m_im_j}{m_i+m_j}, \vec{v} = \vec{v}_i - \vec{v}_j\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{V} = \frac{m_i\vec{v}_i - m_j\vec{v}_j}{M}\!} . Finally, defining Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\!} as the sum of the new center of mass kinetic energy and relative kinetic energy, the integrated mean can be rewritten as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\sigma v\rangle(T) = (\frac{8}{\mu \pi})^{1/2} \frac{1}{(kT)^{3/2}}\int_0^{\infty} E\sigma(E)e^{-E/kT}dE}

We now move to applications, and actual types of reactions. First considered are resonance reactions. These reactions have enhanced probabilities at energies corresponding to the energy levels of one of the nuclei involved in the collision. This approach to modeling the integrated mean is often valid at low T, and is approximated by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\sigma v\rangle_{res,n} \approx \hbar^2 (\frac{2\pi}{\mu kT})^{3/2}\frac{(2J_n+1)(1+\delta_{ij})}{(2I_i+1)(2I_j+1)}\frac{\Gamma_{j,n}\Gamma_{o,n}}{\Gamma_n}e^{-\frac{E_n}{kT}}\!} .

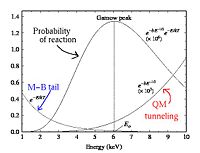
Non-resonant reactions are a bit different to model, and must be handled by type in order to properly define the cross section and velocity.For non-resonant, neutron-type reactions, we return to the 2nd order approximation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma\!} near the Gammow peak where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(0)\!} is nearly constant. With this substitution and use of the equation defining Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma\!} in terms of the S-factor, the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\sigma v\rangle_{nonres}\!} becomes the following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\sigma v\rangle_{nonres} = S(0) (1\frac{\dot{S(0)}}{S(0)}\frac{2}{\sqrt{\pi}}(KT)^{1/2}+\frac{\ddot{S(0)}}{S(0)}\frac{3}{4}kT)}

For charged particle-based non-resonant reactions, the use of the S-factor remains, however the correction term, as well as the basic form of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\sigma v\rangle_{nonres}\!} , are changed to compensate for the presence of a Coulomb barrier in the interaction. With this, the integrated mean is now defined in terms of a default, ground-state energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0\!} and the width of the Gamow region, /Delta (see homework for derivations of these factors) which that it is expressed as the following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\sigma v\rangle_{nonres} = (\frac{2}{\mu})^{1/2}S_{eff}(0)\frac{\Delta}{(kT)^{3/2}}e^{- \tau}}

For charged particle reactions, the relevant cross section that overlaps the Maxwell-Boltzmann distribution function is much larger than kT, which is very different then what is seen in non-resonant neutron reactions. As the energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0\!} gets smaller and smaller, it is clear that the probability that the reaction occurs decreases rapidly due to a smaller and smaller Coulomb tunneling probability.

There are more types of reactions that occur with non-Boltzmann components, and to model them, the concept of reverse reactions must be established. At very high temperatures, i.e. in astrophysical plasma objects, reactions can occur in both the exoergic forward direction and endoergic reverse direction. Assuming a Maxwellian distribution function, the ratio of the reaction cross sections is given by the following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\sigma_i(j,o)_J}{\sigma_m(o,j)_J} = \frac{1+\delta_{ij}}{1+\delta_{om}}\frac{g_og_m}{g_ig_j}\frac{k_o^2}{k_j^2}} ;where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g\!} is the temperature-dependent partition function for the particle.

With use of this, the first reaction process examined is photodisintegration. Photodisintegration is a process where an extremely high energy gamma ray interacts with an atomic nucleus and causes it to enter and excited state which immediately grows through a decay, emitting a proton or neutron. This process is responsible for some of the nucleosynthesis of some of the heavy proton rich elements via the p-process that occurs in supernovae. Here, the wavelength, ergo the energy, of the photon relative to the reaction rate is given by the expression:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{i;\gamma,o}(T) = \frac{g_oG_m}{(1+\delta_{om})G_i}(\frac{\mu_{om}kT}{2\pi \hbar^2})^{3/2}e^{-Q_{o,\gamma}/kT}\langle \sigma v \rangle_{m;o,\gamma}}

A second non-Boltzmann reaction is that of electron capture at high densities. At very high densities, the probability of decay by emitting a positron decreases and thus electron capture again becomes a favored channel of decay. This type of reaction occurs often in the r-process, where the electrons in the supernovae or neutron star can be modeled as a degenerate Fermi gas with energy given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_F = \frac{\hbar^2}{2m_e}(3\pi^2N_A)^{2/3}(\rho Y_e)^{2/3}\!} .

Finally, the last non-Boltzmann reaction discussed is that of inelastic neutrino scattering, which is also prevalent in neutron stars and Type II supernovae. Here the bombardment of a nucleon with a neutrino causes fragmentation, conserving the momentum of the particles by changing the kinetic energy. At very high energies, this fragmentation actually breaks the target nucleus into many other particle, and thus is named "deep" inelastic scattering. Simpler inelastic scattering, like that seen in neutron stars and supernovae, involves the knockout of a proton, neutron, or alpha particle by the weak interaction of the neutrino with the target nucleus.

Nuclear Networks

Within nuclear physics and especially nuclear astrophysics, it is often necessary to look at numerous processes working together as opposed to a single reaction. These "cycles" are extremely important in astrophysics when studying nucleosynthesis, as they offer an explanation as to how the elements were formed. What this means is that after a reaction occurs, the products of the first reaction go on to complete a second, and so on. Some examples include the Hydrogen burning process to form Helium and the CNO cycle.

Whilst determining rates for a secondary or tertiary reaction, it is important to take into account the rates of the prior reactions. In many reaction networks, there will be one process that will take much longer than the others, and therefore determine the rate of the overall reaction. These rate limiting steps are usually processes which involve the weak interaction such as beta decay. These reactions occur on much longer time scales relative to the strong interaction, and thus will limit the overall rate. A general equation for the rate of change of abundance of a nuclei within a nuclear reaction network is as follows.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial n_i}{\partial t}=\sum_{i}n_j^i r_j + \sum_{j,k} n_{j,k}^i r_{j,k} }

The first term represents all of the contributions to the rates from processes that create the particular nucleus, where the second term represents processes that destroy the nucleus being studied.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{1}H(p,e^+\nu_e)^2H}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{2}H(p,\gamma)^3He}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{3}H(^3He,2p)^4He}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{Y}_1= -\frac{2}{2}\rho N_A\left \langle 1,1 \right \rangle Y_1 ^2 - \rho N_A\left \langle 1,2 \right \rangle Y_1 Y_2 + \frac{2}{2}\rho N_A\left \langle 3,3 \right \rangle Y_3 ^2}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{Y}_2= \frac{1}{2}\rho N_A\left \langle 1,1 \right \rangle Y_1 ^2 - \rho N_A\left \langle 1,2 \right \rangle Y_1 Y_2}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{Y}_3= \rho N_A\left \langle 1,2 \right \rangle Y_1 Y_2 -\frac{2}{2}\rho N_A\left \langle 3,3 \right \rangle Y_3 ^2}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{Y}_4=\frac{1}{2}\rho N_A\left \langle 3,3 \right \rangle Y_3 ^2}