S=1/2 and S=1 one dimensional quantum magnets

Magnetism in One Dimension

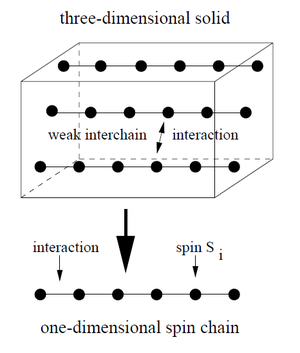
Why are we interested in one-dimensional magnetism? Magnetism in one dimension are of highly theoretical interest as well as there are a variety of highly interesting experimental systems. Most two-dimensional magnets order at T=0, however, in one-dimensional situation, fluctuations are so strong that at T=0 most magnets are disordered. Because of the strong fluctuations, conventional techniques are normally not applicable. So we need to search for new tools to solve problems. One of the representative way is to use numerical methods. An example is, by numerically evaluation, one found a unique, disorder ground state of the nearest-neighbor isotropic anti-ferromagnetic Heisenberg chain for spins S=1/2, with anti-ferromagnetic spin-spin correlations, referred as quasi long-range ordered.

Source: Ulrich Schollwock[1]

Haldane's Conjecture

Haldane conjectured a fundamental difference between spin chains with S an integer and S a half-integer. He mapped out anti-ferromagnetic isotropic Heisenberg chains to an effective low-energy long-wavelength field theory.