Electron-phonon interactions and Kohn anomalies
Electron-phonon interactions
The study of interactions between electrons and phonons, is an interesting and classical topic in quantum many body theory as well as condensed matter physics. The electron-phonon interaction leads to many novel properties in metals, for instance, electrical resistance, thermal resistance, superconductivity and the renormalization of linear electronic specific heat. [1]
Free electrons in lattice
In contrary to the independent electron model, where electrons experience weak periodic potential, the interaction of an electron with all other electrons and nuclei is represented by ‘effective potential’ in some average way, in the tight-binding approximation, electrons move in strong periodic potentials which cannot be approximated by an average background. In this situation, we can assume that the atoms are very widely separated and atomic orbitals remain undistorted.
As an example, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^+_2} problem will be revisited in the second quantization language. States Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1>} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |2>} denote the states of electrons locate on atom 1 and 2, respectively. The state of the two-electron system is thus given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_1, n_2>} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_i>} is the occupation number for each atom. Define creation and annihilation operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^+_i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_i} , which obey anti-commutation relations:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{c_i, c^+_j\right\}=\delta_i,j} ,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{c_i, c_j\right\}=0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{c^+_i, c^+_j\right\}=0} .
The Hamiltonian has the following form:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=E_0(c^+_1c_1+c^+_2c_2)-t(c^+_1c_2+c^+_2c_1)}
Note that this Hamiltonian is non-diagonal. In order to diagonalize it, we could define the following bonding and anti-bonding operators:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_B=1/\sqrt{2}(c_1+c_2)}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_A=1/\sqrt{2}(c_1-c_2)}
Both bonding and anti-bonding operators obey anti-commutation relations. The Hamiltonian can be expressed by these operators as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=(E_0+t)c^+_Ac_A+(E_0-t)c^+_Bc_B}
The state of the system is thus given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_A, n_B>} .
It is easy to generalize the above single molecule problem to electrons moving in crystal. Assume that the tight binding approximation is valid and only one atomic orbital (say, orbital A) is taken into consideration. Moreover, assume that only nearest neighbor hopping term is significant. The Hamiltonian of the system is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=E_A\sum_{i,\sigma}c^+_{i,\sigma}-t_A\sum_{<i,j>,\sigma}(c^+_{i,\sigma}c_{j,\sigma}+c^+_{j,\sigma}c_{i,\sigma})}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <i,j>} means that the summation goes over only nearest neighbor sites. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_i} is the site position and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{i,\sigma}} is the annihilation operator which destroys one electron in orbital A at site i with spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} . Apply Fourier transformation on electron operator
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{\vec{p},\sigma}=\frac{1}{\sqrt{N}}\sum_{j} e^{i\vec{p}\cdot\vec{R_j}}c_{j,\sigma}}
The momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p}} is defined in the first Brillouin zone. Hence, the Hamiltonian can be written in terms of the operators in momentum space as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{\vec{p},\sigma}E_{\vec{k}}c^+_{\vec{k},\sigma}c_{\vec{k},\sigma}}
Phonons: crystal vibrations
Lattice vibrations in a 3D crystal is a realistic model for the study of sound waves. Dynamics of lattice vibration generates phonon propagation in crystal. Let us first ignore the the discret properties of crystal and treat it as a continuous media. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}(\vec{r})} be the displacement field which describes the elastic deformations of media. For small fluctuations, the kinetic energy is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T=\frac{1}2\rho_0\int{d^3\vec{r}|\dot{\vec{u}}(\vec{r})|^2}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_0} is the mass density. The potential energy is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=\frac{1}2\rho_0\int{d^3\vec{r}}\{\Gamma_L(\vec{\nabla})^2+\Gamma_T\vec{\nabla}\times{\vec{u}}|^2\}}
The first term is from longitudinal contribution and the second term is from transverse contribution. However, these expressions are too crude to describe lattice vibrations in general.
If we abandon the ‘continuum’ frame and treat the crystal as a discrete lattice system, the Hamiltonian has the following form
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{j}\frac{P^2_j}{2M}+U(\vec{r}_1,…,\vec{r}_N)}
where j denotes the lattice sites and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}_j=\vec{R}_j+\vec{u}_j} . Assume that the adiabatic approximation is valid, due to the more massive nuclei than electrons. In this sense, the electrons could follow the movement of nuclei quite fast as if they are fixed on nuclei and move together. Within harmonic approximation, we could expand the potential energy U in Taylor series up to the second order:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(\vec{r}_1,…,\vec{r}_N)=U(\vec{R}_1,…,\vec{R}_N)+\sum^{N}_{j=1}\vec{u}_j\cdot\vec{\nabla}_jU|_{\vec{r}=\vec{R}}+\frac{1}2\sum_{j,k}(\vec{u}_j\cdot\vec{\nabla}_j)(\vec{u}_k\cdot\vec{\nabla}_k)U|_{\vec{r}=\vec{R}}+\cdot\cdot\cdot }
Since the atoms do not experience net force at the equilibrium positions, the first order linear term vanishes. Hence,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U-U_{eq}=\frac{1}2\vec{u}_j\cdot\vec{D}_{jk}\cdot\vec{u}_k=\frac{1}2u^{\mu}_jD^{\mu\nu}_{jk}u^{\nu}_k}
where the elastic tensors are defined as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{D}_{jk}=\vec{\nabla}_j\vec{\nabla}_kU}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{D}^{\mu\nu}_{jk}=\partial_{r^{\mu}_j}\partial_{r^{\nu}_k}U}
For a Bravais lattice, the Hamiltonian can be expressed as a set of coupled harmonic oscillators:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_L=\sum_j\frac{P^2_j}{2M}+\frac{1}2\sum_{j,k}\vec{u}_j\cdot\vec{D}_{jk}\cdot\vec{u}_k}
We can use classical approach to analyze the normal modes of lattice vibrations. The classical equation of motion is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\ddot{\vec{u}}_j=-\vec{\nabla}_jU=-\vec{D}_{jk}\cdot\vec{u}_k}
It is reasonable to assume that the solution of the above equation has the plane wave form
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}_j=e^{-i\omega t}e^{i\vec{K}\cdot\vec{R}_j}\hat{\epsilon}(\vec{K})\tilde{u}(\vec{K})}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\epsilon}} is the polarization vector and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{u}} is the amplitude. Substitute it to the equation of motion, we can get
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -M\omega^2\tilde{\epsilon}(\vec{K})=-\sum_k\vec{D}_{jk}\cdot\hat{\epsilon}(\vec{K})e^{i\vec{K}\cdot(\vec{R}_k-\vec{R}_j)}}
The Fourier transform of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{D}} is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{D}(\vec{K})\equiv\sum_k\vec{D}_{jk}e^{i\vec{K}\cdot(\vec{R}_k-\vec{R}_j)}}
Let's introduce the branch index Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda } to label different branches. The polarization vectors are eigenvectors for the diagonalizied Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{D}(\vec{K})} ; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{D}(\mathbf{k})\mathbf{\epsilon}_{\mathbf{k}_\lambda} = K_{\mathbf{k}_\lambda} \mathbf{\epsilon}_{\mathbf{k}_\lambda}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon}_{\mathbf{k}\lambda}\cdot \mathbf{\epsilon}_{\mathbf{k}\lambda^\prime} = \delta_{\lambda,\lambda^\prime} }
Thus, the equation of motion can be written as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\omega^2\mathbf{\epsilon}_{\mathbf{k}\lambda} = \mathbf{D}(\mathbf{k})\mathbf{\epsilon}_{\mathbf{k}_\lambda} = K_{\mathbf{k}_\lambda} \mathbf{\epsilon}_{\mathbf{k}_\lambda}}
The solution for this problem is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u}_{\mathbf{k} \lambda }( \mathbf{R}^0_1, t) = \mathbf{\epsilon}_{\mathbf{k}\lambda}e^{i(\mathbf{k\cdot R}^0-\omega_{\mathbf{k}\lambda }t)} }
Lattice Vibration and Phonons in 1D
As a simple example, let us consider 1D chain of atoms coupled to their nearest neighbors within harmonic approximation, as shown in Fig. 1. The potential energy is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=\frac{1}2\lambda\sum_n(x_{n+1}-x_n-a)^2}
where a is the equilibrium distance between to atoms. Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_n=x_n-R_n} , we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=\frac{1}2\lambda\sum_n(u_{n+1}-u_n)^2}
After taking derivatives, we can get the elastic tensor expressed as
Do the Fourier transformation we have <br\>
Thus, , with the solution of
In the long-wavelength limit, the vibration frequency vanishes linearly as a function of K. The speed of sound wave, which is the slope of the dispersion relation around , is given by
The Hamiltonian is
Use the Fourier transforms variables :
The Hamiltonian becomes
combine and into annihilation and creation operators and
- ,
- ,
where
In general case, we introduce index as the different branches. The Hamiltonian becomes
Acoustical and Optical Phonon in 3D
In moatomic Bravais lattice.
Derivation of Hamiltonian Electron-Phonon Coupling
The Hamiltonian for the electron-phonon interaction can be split info
Where
Let's the ion is placed at the position , at displacement from the ionic equilibrium position, .
expand in powers of
with Bloch waves condition
Let's
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{W}_{\mathbf{kk}^\prime} = \int d^3r \phi^*_{\mathbf{k^\prime}\sigma(\mathbf{r})}\phi_{\mathbf{k}\sigma}(\mathbf{r}) \nabla_{\mathbf{R}^0_i} V(\mathbf{r}-\mathbf{R}^0_i) }
By 2nd-quantization from phonon system
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u}_i(t) = \frac{1}{\sqrt{NM}} \sum_{\mathbf{k}\lambda} Q(\mathbf{k},t) \mathbf{e}^\lambda (\mathbf{k}) e^{i\mathbf{k}\cdot\mathbf{R}^0_i} }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q_\lambda(\mathbf{q}) =\frac{1}{2\omega_\lambda(\mathbf{q})}(b_\lambda(\mathbf{q})+ b^\dagger_\lambda(-\mathbf{q}) ) }
The vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{e}^\lambda(\mathbf{k}) } are the polarization vectors of the modes with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_\alpha \mathbf{e}^\lambda(\mathbf{k}) \cdot \mathbf{e}^{\lambda^\prime}(\mathbf{k}) = \delta_{\lambda \lambda^\prime} }
Therefore,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{int} = \sum_{\mathbf{k k}^{\prime} \sigma } c^{\dagger}_{\mathbf{k}^\prime \sigma} c_{\mathbf{k}^\prime \sigma}\sum_j\mathbf{W}_{\mathbf{kk}^\prime}e^{i(\mathbf{k}-\mathbf{k}^\prime)\cdot\mathbf{R}^0_j}\frac{1}{\sqrt{NM}}\sum_{\mathbf{q}\lambda}Q_\lambda(\mathbf{q}) \mathbf{e}^\lambda(\mathbf{q})e^{i\mathbf{q}\cdot\mathbf{R}^0_j} }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \sum_{\mathbf{k k}^{\prime} \sigma } \sum_\lambda c^{\dagger}_{\mathbf{k}^\prime \sigma} c_{\mathbf{k}^\prime \sigma} (\mathbf{W}_{\mathbf{kk}^\prime}\cdot \mathbf{e}^\lambda(\mathbf{q})) Q_\lambda(\mathbf{q}) \sqrt{\frac{N}{M}} }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \equiv \sum_{\mathbf{k k}^{\prime} \sigma \lambda} g_{\mathbf{kk}^\prime \lambda} c^{\dagger}_{\mathbf{k}^\prime \sigma} c_{\mathbf{k}^\prime \sigma}(b_\lambda(\mathbf{q})+ b^\dagger_\lambda(-\mathbf{q}) ) }
where the electron-phonon coupling constant is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_{\mathbf{kk}^\prime \lambda} = (\mathbf{W}_{\mathbf{kk}^\prime}\cdot \mathbf{e}^\lambda(\mathbf{q}))\sqrt{\frac{N}{2M\omega^{ion}_{pl}(\mathbf{q})}} }
Feynman diagrams of electron-phonon coupling
For a system composed of N electrons, the Hamiltonian for electron-phonon interaction has the general form of
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{ep}=\sum_k\epsilon_kc^+_kc_k+\sum_q\omega_qb^+_qb_q+\sum_{kq}M_qc^+_kc_{k-q}(b^+_{-q}+b_q)}
Introduce an external phonon source term Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{-q}\phi_q} to the Hamiltonian:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{ep}=\sum_k\epsilon_kc^+_kc_k+\sum_q\omega_qb^+_qb_q+\sum_{kq}M_qc^+_kc_{k-q}\phi_q+\sum_qJ_{-q}\phi_q}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_q=b^+_{-q}+b_q}
The Green function is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(k,t;k\prime,t\prime)=-i<T\{c_k(t)c^+_{k\prime}(t\prime)\}>}
and
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D(q,t;k\prime,t\prime)=\frac{\delta<\phi_q(t)>}{\delta J_{q\prime}(t\prime)}=-i(<T\{\phi_q(t)\phi^+_{q\prime}(t\prime)\}>-<\phi_q(t)><\phi^+_{q\prime}(t\prime)>)}
Based on the equation of motion for electron annihilation operator, we can get a differential equation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(k,t;k\prime,t\prime)} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [i\frac{\partial}{\partial t}-\epsilon_k]G(k,t;k\prime,t\prime)+i\sum_qM(q)<T\phi_q(t)c_{k-q}(t)c^+_{k\prime}(t\prime)>=\delta_{kk\prime}\delta(t-t\prime)}
The expectation value of the time-ordered product is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -i<T\phi_q(t)c_{k-q}(t)c^+_{k\prime}(t\prime)>=\frac{\delta<Tc_{k-q}(t)c^+_{k\prime}(t\prime)>}{\delta J_{-q}(t\prime\prime)}-i<\phi_q{t\prime\prime}><Tc_{k-q}(t)c^+_{k\prime}(t\prime)>=\frac{\delta G(k,t;k\prime,t\prime)}{\delta J_{-q}(t\prime\prime)}-i<\phi_q(t\prime\prime)>G(k,t;k\prime,t\prime)}
Along with the expression for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D(q,t;k\prime,t\prime)} , we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [i\frac{\partial}{\partial t}-\epsilon_k]G(k,t;k\prime,t\prime)-\sum_qM(q)<\phi_q(t)>G(k-q,t;k\prime,t\prime)+i\sum_qM(q)G(k-q,t;k_1,t_1)\frac{\delta G^{-1}(k_1,t_1;k_2,t_2)}{\delta<\phi(q_3,t_3)>}G(k_2,t_2;k\prime,t\prime)D(q_3,t_3,-q,t)=\delta_{k,k\prime}\delta(t-t\prime)}
The free electron Green’s function is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{-1}_0(k,t;k_2,t_2)=[[i\frac{\partial}{\partial t}-\epsilon_k]\delta_{k_2,k}-M(k-k_2)<\phi_{k-k_2(t)}>]\delta(t_2-t)}
The vertex function is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma(k_1,t_1,k_2,t_2,q_3,t_3)=-\frac{1}{M(q_3)}\frac{\delta G^{-1}(k_1,t_1;k_2,t_2)}{\delta<\phi(q_3,t_3)>}}
and
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Sigma(k,t,k_2,t_2)=i\int dt_1dt_3\sum_{q,k_1,q_3}M(q)M(q_3)G(k-q,t,k_1,t_1)\Gamma(k_1,t_1,k_2,t_2,q_3,t_3)D(q_3,t_3;-q,t)}
If the fact of momentum conservation is taken into consideration, we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(k)=G_0(k)+G_0(k)\Sigma(k)G(k)}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D(q)=D_0(q)+D_0(q)\Pi(q)D(q)}
Via the vertex function , self energies can be expressed as
The resulting Feynman diagrams are shown in Fig. 2.
Since the Green’s function is an infinite series of diagrams itself, the vertex function is also an infinite series of diagrams. In the condition that the variation of phonon field is much smaller compared with external sources, the vertex function can be expressed as
To the lowest order in and , the vertex function can be expressed as follows:
Electron-phonon interaction in the lattice model
In the isotropic case for normal (IN)
<br\> In the isotropic case for normal acoustical phonon process
The coupling constant
Jellium model
the ion plasme frequence
In order to describe electron-phonon interactions in solids as well as demonstrate their electronic and phononic properties, Jellium model turns out to be set as a right scheme and could give accurate characterization on the system. The main approximation made in this model is to ignore the discrete nature of the ionic system and treat the nuclei as positively charged, continuous and homogenous fluid, with negatively charged electrons moving among the ‘Jellium sea’.
The Hamiltonian for a charge neutral system with electrons embedded in nuclei background and only the Coulomb interaction is taken into consideration:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=-\frac{\hbar^2}{2m}\sum_{\sigma=\uparrow,\downarrow}\int d^3r\Psi^+_{\sigma}(\vec{r})\nabla^2\Psi_{\sigma}(\vec{r})-\sum_{\sigma}\int d^3r\int d^3r\prime\Psi^+_{\sigma}(\vec{r})\Psi_{\sigma}(\vec{r})\frac{e^2}{|\vec{r}-\vec{r\prime}|}e^{-\frac{|\vec{r}-\vec{r\prime}|}{\xi}}n_b(r\prime)+\frac{1}2\sum_{\sigma,\sigma\prime}\int d^3r\int d^3r\prime\frac{e^2}{|\vec{r}-\vec{r\prime}|}e^{-\frac{|\vec{r}-\vec{r}\prime|}{\xi}}\Psi^+_{\sigma}(\vec{r})\Psi^+_{\sigma\prime}(\vec{r}\prime)\Psi_{\sigma\prime}(\vec{r}\prime)\Psi_{\sigma}(\vec{r})+\frac{1}2\int d^3r\int d^3r\prime n_b®\frac{e^2}{|\vec{r}-\vec{r}\prime|}e^{-\frac{|\vec{r}-\vec{r}\prime|}{\xi}}n_b(r\prime)}
For the case of uniform background density,
where N is the total number of atoms and V is the volume of the system. Monoatomic molecules are assumed in this case.
The last term in the Hamiltonian is
As goes to infinity, this term diverges. So, should be kept finite since now on.
The second term in the Hamiltonian is
For the third term in Hamiltonian, perform Fourier transform on :
They obey anti-commutation relation in momentum space:
Transfer to the center of mass coordinates:
- ,
Thus the second term in Hamiltonian can be written as
- Failed to parse (syntax error): {\displaystyle \frac{1}{2}\sum_{\sigma\sigma\prime}\int d^3r\int d^3r\prime\frac{e^2}{|\vec{r}-\vec{r}\prime|}e^{-\frac{|\vec{r}-\vec{r}\prime|}{\xi}}\frac{1}{V^2}\sum_{\vec{k}_1,…\vec{k}_4}e^{-i\vec{k}_1\cdot\vec{r}}e^{-i\vec{k}_2\cdot\vec{r}\prime}e^{i\vec{k}_3\cdot\vec{r}\prime}e^{i\vec{k}_4\cdot\vec{r}}\Psi^+_{\vec{k}_1,\sigma}\Psi^+_{\vec{k}_2\sigma\prime}\Psi_{\vec{k}_3,\sigma\prime}\Psi_{\vec{k}_4,\sigma} =\frac{1}{2}\sum_{\sigma\sigma\prime}\frac{1}{V^2}\sum_{\vec{k}_1,…\vec{k}_4}\Psi^+_{\vec{k}_1,\sigma}\Psi^+_{\vec{k}_2\sigma\prime}\Psi_{\vec{k}_3,\sigma\prime}\Psi_{\vec{k}_4,\sigma}\int d^3R\int d^3r\frac{e^2}{|\vec{r}|}e^{-\frac{|\vec{r}|}{\xi}}e^{-i(\vec{k}_1-\vec{k}_4)(\vec{R}+\frac{1}{2}\vec{r})}e^{-i(\vec{r}_2-\vec{k}_3)(\vec{R}-\frac{1}{2}\vec{r})} =\frac{1}{2}\sum_{\sigma\sigma\prime}\frac{1}{V}\sum_{\vec{k}_1,…\vec{k}_4}\delta_{\vec{k}_1-\vec{k}_4,\vec{k}_2-\vec{k}_3}\Psi^+_{\vec{k}_1,\sigma}\Psi^+_{\vec{k}_2\sigma\prime}\Psi_{\vec{k}_3,\sigma\prime}\Psi_{\vec{k}_4,\sigma}\int d^3r\frac{e^2}{|\vec{r}|}e^{-\frac{|\vec{r}|}{\xi}}e^{-i(\vec{k}_1-\vec{k}_4-\vec{k}_2+\vec{k}_3)\frac{1}{2}\vec{r}}}
Let and , and
Then
The third term in Hamiltonian has the following form:
For the integral over r,
So, this term can be written as
Assume that the system is charge neutral, , then the Hamiltonian is finally given by
The partition function is given by
where the action function for interaction part is
Cumulant expansion is applied to the analysis of interactions in Jellium model. Expand the interaction part in partition function and keep to the second order:
The partition function for non-interacting system is given by
The first order correction to action function is
The second order correction to the action function is given by
So,
After expanding the above expression, there are in total 24 terms. However, 4 of them are disconnected terms which force , thus only 20 terms are left for further calculation.
Since the term can be trivially derived from the first order correction , let us focus on the term <S_{int}^2>. Expand through contraction, we could get three block terms, which are denoted by , and , respectively. Calculate these three parts one by one.
Upon shifting variables , , we have
For
Upon shifting variables and then , we have
This term gives finite contribution to the second order correction.
For
Upon shifting variables , , and then , we have
This term is divergent and thus gives infinite contribution to the second order correction.
Linear response calculations of electron-phonon interactions
In the strong-coupling theory of superconductivity, the electron-phonon spectral distribution function and its first reciprocal moment , are two most essential quantities which are fully demonstrated by electron-phonon interactions. There exist several approaches to calculate the first reciprocal moment. One is only to calculate electronic contribution [2] and the information about phonon frequencies and eigenvectors is got from inelastic neutron-scattering data [3]. Alternatively, the electron-phonon interaction may be calculated via frozen-phonon total-energy approach. However, these listed approaches are too crude to estimate some critical quantities, like critical temperature () in phase transition.
Linear response method is based on solid-state Sternheimer method [4] and can produce accurate phonon dispersion relations as well as eigenvectors for arbitrary . In solid-state Sternheimer method, the electron-phonon spectral distribution function is given by
where is the summation over the first Brillouin zone, and is the density of states for electrons at Fermi level. is the phonon line-width which is derived from Fermi golden rule:
where denotes energies with respect to Fermi level, and is the electron-phonon interaction matrix element whose physical meaning is the probability of scattering from state to state via phonon .
Let to be the finite orbital basis, the electron-phonon interaction matrix element is thus given by
where is the coefficient of basis in the basis , and is the changes in one electron potential, is the changes of basis due to electron-phonon interaction. This expression gives a correct behavior in the long-wavelength limit.
Due to some phase-space reasons, such as Fermi surface nesting, the phonon line-width could show violent variations in the first Brillouin zone, as a result of which, the calculation for electron-phonon spectral distribution function will be performed on a rather dense mesh. However, , the phonon frequency, is a relatively smooth function of and it is not necessary to calculate it on such a dense mesh. Via transforming the dynamical matrix from momentum space to real space, together with diagonalization, the phonon frequencies and eigenvectors for arbitrary can be reached.
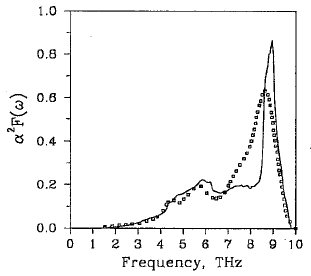
The linear response calculations of electron-phonon interactions have a general agreement with experimental results, which accounts for the validity of this method in analysis electron-phonon coupling problem. For instance, for the most abundant metal on earth, aluminum (Al) displays a nice consistence between theoretical calculation and tunneling measurements on electron-phonon spectral distribution function. Fig 5 shows the comparison.
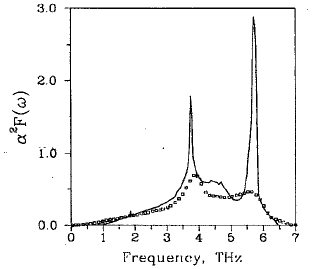
Niobium (Nb) is one the well-studied elemental superconductors, with a relatively high critical temperature . Compared with tunneling measurements, the theoretical calculations yield stronger electron-phonon coupling, and the shape of electron-phonon spectral distribution function is broadened, as shown in Fig 6.
Kohn anomalies
Screening
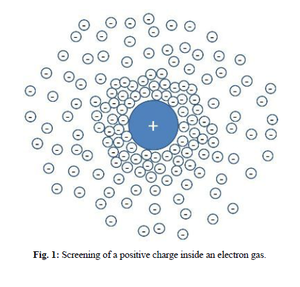
What is a free electron gas? A metal can be considered as an ionic lattice embedded inside an electron sea. The periodic ion lattice causes a periodic potential, which is very hard to calculate. Therefore, we often adopt the free electron model which treats the ions as a uniform background of positive charge even for real metals. This is called a free electron gas.
Screening is an important phenomena in a free electron gas. When an external positive charge density is applied, the electrons will be attracted to surround the positive charge. The re-arrangement of the electrons generates an induced charge distribution . Therefore, the total charge density = + is less positive than . Thus, The total potential is weaker than the external potential caused by the positive charge only. The phenomenon is called screening. By assuming that the applied charge is weak enough so that the total potential and external potential are linearly related, we get the following function in momentum space.
is the Fourier transform of the dielectric constant, is the wave vector of the field, is the Fourier transform of induced charge density, and is the Fourier transform of the total potential.
Kohn anomalies
The lattice vibration of the ions in a metal are partly screened by the conduction electrons. We shall see that this screening changes rather rapidly on certain surfaces in the space of phonon vectors and that therefore on surfaces the frequencies vary abruptly with . And is a continuous function of but that on the surfaces, [2]
The location of these surfaces is entirely determined by the shape of the electronic Fermi surface.
Here we use the above free electron model for calculation. For an embedded charge distribution,
,
the induced electronic charge density is:
,
where
,
here is the Bohr radius. Note that near ,
,
and
,
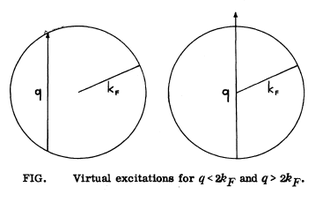
this equation shows an abrupt decrease of the ability of the electrons to screen the embedded charge distribution as soon as exceeds . [2]
the scattering of a quasi-particle from a point to a point in momentum space with . Energy and momentum conservation require that both and lie on the Fermi surface. This immediately introduces a restriction on the phonon wave vector : phonon wave vectors connecting nested parts of the Fermi surface will strongly interact with the electrons leading to a large phonon damping, whereas those which do not span the Fermi surface will not interact with electrons. Kohn pointed out that the interaction of phonons with the conduction electrons in a metal should cause anomalies in the phonon spectra.
As long as , causes virtual excitations of some electrons with conservation of energy. When such excitations are no longer possible.
Now a lattice vibration of wave vector produces a change of ionic charge density of the form
,
where are the reciprocal lattice vectors.
Therefore we expect an abrupt change of the restoring force whenever is such that, for some reciprocal lattice vector ,
,
on the surfaces in space defined by this equation.[2]
The strength of the Kohn anomaly depends on the joint density of occupied and unoccupied electronic states. If their quantity is large, conduction electrons may, become unstable with respect to a spatially inhomogeneous perturbation. To first order, the response of the electrons to such a perturbation is measured by the generalized susceptibility .
References
- ↑ Yun-Chieh Peng. Stanford University. Winter, 2007. http://large.stanford.edu/courses/2007/ap272/peng1/
- ↑ Jump up to: 2.0 2.1 2.2 2.3 W. Kohn, Phys. Rev. Lett 2, 393 (1959)

![{\displaystyle D(K)=2\lambda [1-cosKa]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ce3a8fecc2a22c45f88c1631271a9d2c75a0e37)




![{\displaystyle H_{ph}=\sum _{j=1}^{N}[{\frac {1}{2M}}p_{j}^{2}+{\frac {1}{2}}\lambda (u_{j}-u_{j-1})^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58ab63f8e07bb675c6941757158b694621c18ee5)


![{\displaystyle H_{ph}=\sum _{k}[{\frac {1}{2M}}p_{k}p_{-k}+{\frac {1}{2}}M\omega _{k}^{2}u_{k}u_{-k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6b5231f57f3a94c80095d1e35e9d84d5ed3eb48)









![{\displaystyle [b_{k_{1}\lambda _{1}},b_{k_{2}\lambda _{2}}^{\dagger }]=\delta _{k_{1},k_{2}},\delta _{k_{1},k_{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49039d41b58b96e9376357edddfa3bb925e608f1)

![{\displaystyle H_{ph}^{0}=\sum _{\mathbf {k} \lambda }\hbar \omega _{\mathbf {k} \lambda }(b_{\mathbf {k} \lambda }^{\dagger }b_{\mathbf {k} \lambda }+{\frac {1}{2}}),[b_{\mathbf {k} \lambda },b_{\mathbf {k} \lambda }^{\dagger }]=\delta _{\mathbf {k,k^{\prime }} }\delta _{\lambda ,\lambda ^{\prime }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75be74ff2c93af1411e26eab70d56c038a7e95af)




















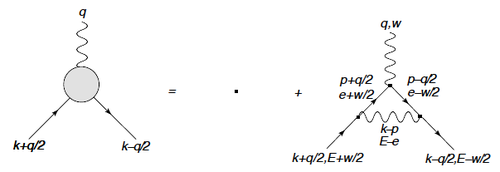

























![{\displaystyle Z=Tr[e^{-\beta ({\hat {H}}-\mu {\hat {N}})}]=Z_{0}<e^{-S_{int}}>=e^{-\beta \Omega }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e6adb70eaeda615c94db976dde1c34471134607)




![{\displaystyle \beta \Omega ^{(2)}=-{\frac {1}{2}}[<S_{int}^{2}>_{0}-<S_{int}>_{0}^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a095f9d113b0d17e7e8382c4c014d8f6f0283a1b)




















































![{\displaystyle F\left(q\right)={\frac {1}{\pi a_{0}q^{2}}}\left[1+{\frac {k_{F}}{q}}\left(1-{\frac {q^{2}}{4k_{F}^{2}}}\right)\ln {\left|{\frac {q+2k_{F}}{q-2k_{F}}}\right|}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b972bbdbd230964255b6e25dc2c94b68ba54a71b)


![{\displaystyle F\left(q\right)={\frac {1}{2\pi a_{0}k_{F}}}\left[1+{\frac {1}{2k_{F}}}\left(q-2k_{F}\right)\ln {\left|{q-2k_{F}}\right|}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f74ed2ae4e12430da305992a424f6c0bda788fb8)







![{\displaystyle \rho _{\text{ion}}\left({\vec {r}}\right)=\sum A_{\nu }exp\left[i\left({\vec {q}}+{\vec {K_{\nu }}}\right)\cdot {\vec {r}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52f9799c137b7d94ff73378f09279379e293554d)




