S=1/2 and S=1 one dimensional quantum magnets

Why are we interested in one-dimensional magnetism? (a) In many cases we have exact solutions (which are lacking in higher dimensions), (b) they exhibit a wealth of ground states, including disordered phases, (c) they are a natural testing ground for methods and approximations, (d) there are a variety of highly interesting experimental systems. Especially in theoretical field that most two-dimensional magnets order at T=0, however, in one-dimensional situation, fluctuations are so strong that at T=0 most magnets are disordered. Because of the strong fluctuations, conventional techniques are normally not applicable. So we need to search for new tools to solve these problems. One of the representative way is to use numerical methods. An example is, by numerically evaluation, one found a unique, disorder ground state of the nearest-neighbor isotropic anti-ferromagnetic Heisenberg chain for spins S=1/2, with anti-ferromagnetic spin-spin correlations, referred as quasi long-range ordered.In theoretical research, Coherent many body wave functions are fascinating and useful in situations of quantum magnets without static order at T=0.

Source: Ulrich SchollwockSource: Ulrich Schollwock

Haldane's Conjecture

Introduction to Haldane's Conjecture

Haldane conjectured a fundamental difference between spin chains with S an integer and S a half-integer. Haldane Conjecture is that there is a spin gap of the excitation spectrum in integer Heisenberg spin chains whereas half-integer spin chains have a gapless excitation spectrum. Here we use effective field theories of anti-ferromagnets to show Haldane's Conjecture.

Effective Field Theories of Antiferromagnets

Let's consider an isotropic anti-ferromagnetic Heisenberg model with nearest neighbor interaction between spins of S length.The Hamiltonian can be expressed as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}=J\sum_{i=1}^N \mathbf{S}_i \mathbf{S}_j \qquad J>0}

Assume that local Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\acute{e}el} order on short length scales, we can derive an effective long-wavelength low energy Lagrangian for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S\rightarrow\infty}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L}=\frac{v}{2g}\partial_{\mu}\overset{\rightarrow}{\phi}\partial^{\mu}\overset{\rightarrow}{\phi}+\frac{\Theta}{8\pi}\epsilon^{\mu\nu}\overset{\rightarrow}{\phi}\left(\partial_{\mu}\overset{\rightarrow}{\phi}\times\partial_{\mu}\overset{\rightarrow}{\phi} \right)}

Where v=2JS is the spin wave velocity, g=2/S is the coupling constant and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Theta=2\pi S} is the topological angle; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{\rightarrow}{\phi}} is a three-component unit vector field. Then we can do a Wick rotation to get the form of Lagrangian as below:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L}=\mathcal{L}_{NL}+i\mathcal{L}_{TOP}}

Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L}_{NL}} is the Lagrangian of an O(3) nonlinear Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} model and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L}_{TOP}=\frac{\Theta}{8\pi}\epsilon^{\mu\nu}\overset{\rightarrow}{\phi}\left(\partial_{\mu}\overset{\rightarrow}{\phi}\times\partial_{\mu}\overset{\rightarrow}{\phi} \right)} .With differential geometry, we are able to derive that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q[\overset{\rightarrow}{\phi}]=\frac{1}{\Theta}\int{d^2 x}\mathcal{L}_{TOP}[\overset{\rightarrow}{\phi}]}

Here Q is an integer for any field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{\rightarrow}{\phi}} . It's called winding number.

The partition function is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D[\overset{\rightarrow}{\phi}]e^{-\int{d^2 x}\mathcal{L}_{NL}}e^{-i\Theta Q[\overset{\rightarrow}{\phi}]}\delta\left( |\overset{\rightarrow}{\phi}|^2 \right)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-i\Theta Q[\overset{\rightarrow}{\phi}]}= \begin{cases} 1 & S=interger \\ \pm 1 & S=half-interger \\ \end{cases} }

For integer S, it's reduced to the nonlinear Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} -model. And for half-integer S,it can be considered by the Bethe ansatz for S=1/2.

Re-normalize group, we can get the below Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} function.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta\left( \mu \right)=a\frac{du}{da}=-\epsilon u+\frac{u^{2}}{2\pi}+O\left( u^{3} \right)}

This function tells us that for any finite S, the flow is to disordered high-temperature limit. Where we regard Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=ga^{2-d}} ,lattice constant a and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon=d-2} .

The correlations are antiferromagnetic. They decay with the Ornsterin-Zernike law for two-dimensional space-time.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \mathbf{S}_i\cdot\mathbf{S}_j \right\rangle\propto\left( -1 \right)^{i-j}\frac{e^{-|i-j|/\xi}}{\sqrt[2]{|i-j|}}}

For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\simeq\pi} , the excitation spectrum is massive-relativistic, with a gap to the ground state and can be depicted as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\left( k \right)=\sqrt[2]{\Delta^{2}+v^{2}\left( k-\pi \right)^2}}

In the limit of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S\rightarrow\infty} , the finite gap and the correlation length should have the relation with S, demonstrated like

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\left( S \right) \propto S^2e^{-\pi S}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi\left( S \right) \propto S^{-1}e^{\pi S}}

In classic limit, at T=0, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{S \to \infty }\Delta=0} ,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{S \to \infty }\xi=\infty}

Microscopic Description of Haldane Magnets: AKLT model

AKLT model is the first exact solvable model that supported Haldane's conjecture. It was proposed by Affleck, Kennedy, Lieb and Tasaki at 1987. For S=1/2, An easy way to form the basis of spin 1/2 antiferromagnet is to list all possible products of contraction of spins which form singlets on two site These singlets are called valence bonds and written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt[]{2}}\left( |\uparrow\downarrow>-|\downarrow\uparrow> \right)} . As for nearest-neighbor hopping S=1/2 Heisenberg model, Bethe had proposed an Ansatz and solved the model exactly. The ground state using Bethe Ansatz has the following properties: power-law correlations and no gap between excited state. As for a special ratio between nearest-neighbor hopping and next-nearest-neighbor hopping, Majumdar and Ghoshgave the two exact ground states with purely nearest-neighbor valence bonds. The ground states of this type have ultrashort-range correlations and an energy gap. Possibly inspired by the fact that valence bonds can form convenient basis for spin systems and that in the Majumdar-Ghosh model the ground state can be expressed by purely nearest-neighbor valence bonds, Affleck, Kennedy, Lieb and Tasaki tried to seek exactyly solvable Hamiltonians for spin-1 system in one dimension(and extended to other dimension and higher spin) whose ground states are constructed simply out of valence bonds. This is AKLT model. The Hamiltonian can be written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{i}P_{2}\left(S_{i}+S_{i+1} \right)} . The ground state of this model,which is called valence bond solid, is unique(compared to degenerate) and does not break symmetries. The ground state has following properties: correlation decay exponentially and a gap exist between excited states. These behaviours support the Haldane's conjecture, i.e. in one dimension, integer spin system has short ranged, nondegenerate phase and gapped excited states. Also, they made a argument that the valence bond solids is a good approximation to the ground state of real spin-1 chain.

In the following, I will first demonstrate the valence bond solids ground state for spin-1 in one dimension, and then prove that it's the ground state of Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{i}P_{2}\left(S_{i}+S_{i+1} \right)} .After that it will be shown that the VBS ground state correlations decay exponentially, and at last a brief argument that there exists a gap to spin excitations.

First, let's generalize valence bond to s=1. I have already mentioned the s=1/2 valence bond. On two nearest-neighbor sites, contract two spins on these two site and form a singlet \frac{1}{\sqrt[]{2}}\left( |\uparrow\downarrow>-|\downarrow\uparrow> \right)., then product these valence bonds in all possible ways to get a basis. Think the spin-1 operator as two symmetrised spin-1/2 operators per site. Contract one spin-1/2 operator of one site with a spin-1/2 operator on one nearest-neighbor site and contract the left spin with another spin on one nearest-neighbor site.

We must not contrast two spins on the same site because this will antisymmetrise. Furthermore, since we imagine that there are two spin-1/2 on each site but actually it's a spin-1, when we exchange two spins on the same site,the state constructed from product of valence bonds should remain the same, instead of change a sign. So we can use a simple notation by drawing two lines from each site and end the lines on the one of the nearest-neighbor sites.

Source: I. Affleck

To see why VBS state is a ground state of the Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{i}P_{2}\left(S_{i}+S_{i+1} \right)} , we can see four spins on two nearest-neighbor sites. Two of the spins have to form a singlet to be a valence bond, and the two remaining spins can form a triplet or a singlet. So the total spin on the two neighboring sites cannot be 2. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{2}} project onto the total spin=2 case for these two sites. That means only total spin=2 contribute to the energy. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{2}=\left(S_{1}+S_{2} \right)^{2}}

Unlike the dimerized s=1/2 ground state, the translational symmetry is not broken

Affleck-Kennedy-Lieb-Tasaki(AKLT) model has explained why excitation are gapped from a microscopic point of view. The AKLT Hamiltonian for a spin chain with spin S=1 is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^{ALKT}_{S1}=\sum_{i}\overset{\rightarrow}{S_i}\cdot\overset{\rightarrow}{S_i+1}+\frac{1}{3}\left( \overset{\rightarrow}{S_i}\cdot\overset{\rightarrow}{S_i+1} \right)^2+\frac{2}{3}}

Here we can obtain a bilinear-biquadratic spin chain.

Source: Ulrich Schollwock

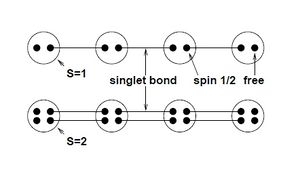
Fig_2 describes the valence bond solid ground state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi^{VBS}>} . From Fig_5, it's easy to see that the maximal spin sum on each bond is S and we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^{ALKT}|\psi^{VBS}>=0} . The symmetric spins are linked by singlet bonds Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt[]{2}}\left( |\uparrow\downarrow>-|\downarrow\uparrow> \right)} . Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^{ALKT}} is a positive sum of projectors, so it doesn't have negative eigenvalues, which leads us to find the ground state.

In fact, with the S=1 case, we can see how the property of both chains are continuously connected

However, it exists limit. The T=0 phase diagram in the semi-classical limit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S\rightarrow\infty} is gotten by the replacement of the quantum spins by commuting unit vector spins.

For half-integer spins, the phase diagram of S=1/2 and S=infinite are very similar, so the classical limit for half-integer is very obvious. However, for S=1 situation, phase diagram is very different. It's not trivial.

Comparison between Heisenberg model and AKLT model

Heisenberg model and AKLT model are both from the Hamiltonian

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\left( \alpha \right)=cos\gamma\sum_{i}\overset{\rightarrow}{S_i}\cdot\overset{\rightarrow}{S_i+1}+sin\gamma\sum_{i}\left( \overset{\rightarrow}{S_i}\cdot\overset{\rightarrow}{S_i+1} \right)^2}

The difference is in Hersenberg model, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma=0} , while in AKLT model Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma=0.1024\pi} .

Concrete Examples

S=1/2 case: the Bethe solution for S=1/2

From Reference ,we can get a view of Bethe solution for S=1/2. Here we will introduce simply about Bethe-Ansatz Solution

Consider the wavefunction for a pure state of N spins. Each spin are of value of one half, labeled by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s\left( n \right)=\pm1/2 \qquad \left( n=1...N \right)} . The total spin can be expressed as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{\rightarrow}{S}=\sum_{n=1}^{N}\overset{\rightarrow}{S}\left( n \right)} . States Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi\left( s\left( 1 \right),...,s\left( n \right) \right)} with M down spins and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( N-M \right)} up spins are used to calculate.The total z component of the spin is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{z}\Psi\left( s\left( 1 \right),...,s\left( N \right) \right)=\left( \sum_{n=1}^{N}s\left( n \right) \right)\Psi\left( s\left( 1 \right),...,s\left( N \right) \right)}

with

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=1}^{N}s\left( n \right)=\frac{N}{2}-M}

In terms of the spin exchange operator P with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{n,m}\Psi\left( s\left( 1 \right),...,s\left( n \right)...,s\left( m \right)...,s\left( N \right) \right)=\Psi\left( s\left( 1 \right),...,s\left( m \right)...,s\left( n \right)...,s\left( N \right) \right)} so we can get the Hamiltonian like

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=J\sum_{n=1}^{N}\left( (P_{n,n+1}-1\right)}

with periodic boundary conditions. In order to satisfy all the functions, Bethe introduced the Bethe-Ansatz

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\left( p_{1},...,p_{M} \right)=\sum_{P\in S_{M}}A_{P}\mu^{n_{1}}_{P_{1}}\cdot\cdot\cdot\mu^{n_{M}}_{P_{M}}} .

After a series of calculations, we get the Bethe Ansatz equations

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( \frac{\chi_{j}+i\frac{\pi}{2}}{\chi_{j}-i\frac{\pi}{2}} \right)^{N}=-\prod_{l=1}^{N}\left( \frac{\chi_{j}-\chi_{l}+i\pi}{\chi_{j}-\chi_{l}-i\pi} \right)}

Also we can see that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda^{N}\equiv\left( \frac{\chi_{j}+i\frac{\pi}{2}}{\chi_{j}-i\frac{\pi}{2}} \right)^{N}=1}

Use Heisenberg Hamiltonian to act on a Bethe-Ansatz wave function, resulting in

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\phi\left( p_{1},...,p_{M} \right)=J\sum_{j=1,P_{j}\neq P_{j+1}-1}^{M}\phi\left( p_{1},...,p_{j}+1...,p_{M} \right)+J\sum_{j=1,P_{j}\neq P_{j-1}+1}^{M}\phi\left( p_{1},...,p_{j}-1...,p_{M} \right)+\left( N-2M \right)J\phi\left( p_{1},...,p_{M} \right)+2J\sum_{j=1,P_{j}\neq P_{j+1}-1}^{M}\phi\left( p_{1},...,p_{j}+...,p_{M} \right)-NJ\phi\left( p_{1},...,p_{M} \right)}

By employing the Bethe Ansatz, we can reduce the Heisenberg Hamiltonian in the form

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\phi\left( p_{1},...,p_{M} \right)=J\sum_{j=1}^{M}[\mu\left( \chi_{j} \right)+\mu^{-1}\left( \chi_{j} \right)-2]\phi\left( p_{1},...,p_{j}+1...,p_{M} \right)-J\sum_{j=1}^{M}[\phi\left( ,...,p_{j}+1,p_{j}+1... \right)-2\phi\left( ,...,p_{j},p_{j}+1... \right)]}

The last term (with brackets) is found to be vanished. Thus the Bethe-Ansatz state is an eigenstate of the Heisenberg model with eigenvalue E given by

E=J\sum_{j=1}^{M}[\mu\left( \chi_{j} \right)+\mu^{-1}\left( \chi_{j} \right)-2]=-J\sum_{j=1}^{M}\frac{\pi^{2}}{\chi_{j}^{2}+\left( \frac{\pi}{2} \right)^{2}}

The solutions to the Bethe-Ansatz equation is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{~}{\rho}=\overset{~}{\rho}_{0}\left( p \right)+\sum_{j=1}^{n}\frac{e^{-ip\theta_{j}}-\frac{\pi|p|}{2}}{2cosh\frac{\pi p}{2}}}

with

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{~}{\rho}_{0}=\frac{N/2}{2cosh\frac{\pi p}{2}}}

Leading to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho\left( \chi \right)=\rho_{0}\left( \chi \right)+\sum_{j}\rho_{hole}\left( \chi-\theta_{j} \right)}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{0}\left( \chi \right)=\frac{N}{2cosh\left( \chi \right)}}

The total number of roots M in a state with n holes is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M=\int_{-\infty}^{+\infty} d\chi\rho\left( \chi \right)-n=\overset{~}{\rho}\left( 0 \right)-n=\frac{N-n}{2}}

M is an integer, n must be even(odd） if N is even (odd). The state has eigenvalue

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=-J\pi^{2}\int d\chi\frac{\sigma\left( \chi \right)}{\chi^{2}+\left( \frac{\pi}{2} \right)^2}}

The density of roots for the Bethe-Ansatz equation is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( \chi \right)=\left( \rho \right)-\sum_{i=1}^{n}\delta\left( \chi-\theta_{i} \right)}

Use Fourier translation, the form represented in Fourier space is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=-J\pi\int dp\overset{~}{\sigma}\left( -p \right)e^{-\frac{\pi|p|}{2}}}

with

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{~}{\sigma}\left( -p \right)=\overset{~}{\rho}\left( -p \right)-\sum_{i=1}^{n}e^{-ip\theta}}

So the final result of energy is described below

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=E_{0}+\sum_{i=1}^{n}E_{h}\left( \theta_{i} \right)}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}} is the ground energy, which can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}=-2NJIn2}

in addition, the "excitation energy", i.e., "holes" can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{h}\left( \theta_{i} \right)=\frac{\pi J}{cosh\theta}}

In order to minimize the energy, we choose the solution with real roots and without holes. The total spin S for the state when N is even is obtained

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=\frac{N}{2}-M=0}

Therefore, the ground state is a singlet with S=0. The excitations are holes with energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi J}{cosh\theta}} . For a lattice which has N sites, where N is even (odd), there exist an even (odd) number of holes. A state with one hole in this way carries Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{z}=+1/2} . You can find the spin-reversed hole by action Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{-}} on the state. Notice that, these states are degenerate because of the SU(2) symmetry.

The Bethe solution for S=1/2 states that for a rather large class of isotropic, translationally and rotationally invariant Hamiltonians, the spectrum is either critical, or the ground state degenerate with broken translational invariance, for example, by dimerisation, and the spectrum gapped. This indicate that the S=1/2 chain is indeed generic for all half-integer spins.

In experimental field, compounds with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cu^{2+}} ions which realize spin 1/2 grabbed the interest of scientists. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle CuCl_{2}\cdot2NC_{5}H_{5}} (Copperpyridinchloride = CPC) is the first quantum chain investigated experimentally.

S=1 case: Haldane Spin Liquid

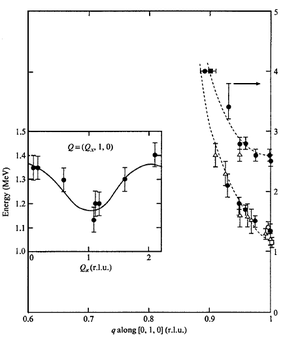
For integer spins, there is no exact analytic result. For S=1, many studies have been carried out to determine the gap, converging to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_{s=1}=0.41050\left( 2 \right)} obtained independently by DMRG and exact diagonalization. Experimentally, this is also reflected on the material side.Most investigations concentrate on compounds with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ni^{2+}} ions which realize spin 1. The gap was first confirmed beyond any doubt by Renard et al., on the standard S=1 chain “NENP” (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [Ni\left( C_{2}H_{8}N_{2} \right)_{2}][ClO_{4}]} ). The experiments showed isotropic interactions with a weak easy-plane anisotropy, which agreed with theoretical results very well.

Source:J.P. Renard.

To understand better, we are introducing the Haldane Spin Liquid. The spin S = 1 Heisenberg chain can be described as a limiting case of two ferromagnetically coupled S = 1/2 chains, i.e. spin ladder.But we have to classify all relevant perturbations which drive the system of two chains to strong coupling.

First, the bare Hamiltonian is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}=\frac{v_{s}}{2}\sum_{j=1,2}\int dx[\Pi^{2}_{j}\left( x \right)+\left( \partial_{x}\phi_{j} \right)^2]}

From bilinear combinations of these fields and from the corresponding current operators one can compose the following relevant perturbations:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{\perp}=\int dx\left( \mathcal{H}_{J}+\mathcal{H}_{twist}+\mathcal{H}_{n,\epsilon} \right)}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{J}=g_{0}[J_{1}\left( x \right)+\overset{-}{J}_{1}\left( x \right)]\cdot[J_{2}\left( x \right)+\overset{-}{J}_{2}\left( x \right)]}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{twist}=g_{1}[n_{1}\left( x \right)\partial_{x}n_{2}\left( x \right)-n_{2}\left( x \right)\partial_{x}n_{1}\left( x \right)]+g_{2}[\epsilon_{1}\left( x \right)\partial_{x}\epsilon_{2}\left( x \right)-\epsilon_{2}\left( x \right)\partial_{x}\epsilon_{1}\left( x \right)]}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{n,\epsilon}=g_{s}n_{1}\left( x \right)\cdot n_{2}\left( x \right)+u\epsilon_{1}\left( x \right)\epsilon_{2}\left( x \right)}

A simple calculation reveal the following expression for the imaginary part of the total magnetization.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Im m \chi^{\left( R \right)}\left( \omega,q \right)=\frac{2^2 q^2 m^2 v_{s}^2}{s^3 \sqrt[]{s^2-4m_{t}^{2}}}}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^2=\omega^{2}-v_{s}^{2}q^2}

Source:Alexei

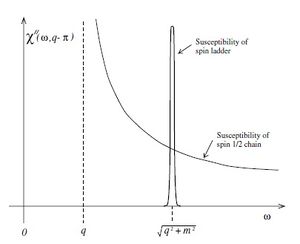
The correlation function of staggered magnetization depends on a mutual sign of the masses. The description of masses can be found below. If you want to read more about it, you can find the detail in this reference book.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m=\frac{g_{s}\lambda^{2}}{2\pi}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{t}=m\left( 1-u/g_{s} \right)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{s}=-m\left( 3+u/g_{s} \right)}

The case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{t}m_{s}<0} corresponds to Haldane spin liquid. The figure next to this part shows that exhibits a sharp single-magnon peak in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi^{''}\left( \omega , q~pi \right)} .

The spin S = 1 Heisenberg chain can be described as a limiting case of two ferromagnetically coupled S = 1/2 chains, two weekly isotropic S=1/2 Heisenberg chains.

Source: NHMFL 11/19/99

Nevertheless, we can comprehend in another simple way about the spin gap of spin 1 AFM (antiferromagnet). As displayed in Fig_3, Magnets with 2S=nz have a nearest neighbor singlet covering. For integer spin chains (S=n, z=2) this state is “close to” the ground state, Excited states are propagating bond triplets separated from the ground state by an energy gap.

Numerical Method to Solve 1-D Quantum Magnets Problem: DMRG

The word DMRG is short for The Density Matrix Renormalization Group.

Various techniques have been introduced: the nonlinear-model, conformal analysis, bosonization, the matrix product ansatz, the Bethe ansatz, exact diagonalization and quantum Monte Carlo are now standard techniques in the field. Among numerical approaches, certainly the most important recent development has been the introduction of the Density Matrix Renormalization Group (DMRG) by White in 1992. It's an effective approach to open one-dimensional quantum magnets paradox.

The T=0 DMRG

The method is a real space renormalization group method, which grows a long chain linearly. For N states per site, the Hilbert space grows as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N^{L}} , such that the Hilbert space must be truncated to a fixed size to manage long systems numerically. The fundamental progress of the DMRG is that it essentially eliminates the arbitrary character of truncation.

One keeps the M states of A' that have highest weight in the ground state of B, i.e. contribute most to the projection of the ground state of B on A'. Writing the ground state of B as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid\Psi\big\rangle_{B}=\sum_{i=1}^{MN}\sum_{j=1}^{MN}\psi_{ij}\mid{i}\big\rangle\mid{j}\big\rangle}

We approximate the ground state as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid\Psi\big\rangle^{approx}_{B}=\sum_{a}^{M}\sum_{j}^{MN}{a}_{\alpha{j}}\mid\alpha\big\rangle\mid{j}\big\rangle}

where the M orthonormal states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid\alpha\big\rangle={\textstyle \sum_{i=1}^{MN} }{u}_{\alpha{i}}\mid{i}\big\rangle} will span the new truncated Hilbert space. The best choice is found by minimizing

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \parallel\mid\Psi\big\rangle_{B}-\mid\Psi\big\rangle^{approx}_{B}\parallel^{2}=1-2\sum_{\alpha{i}{j}}\psi_{ij}{a}_{\alpha{j}}{u}_{\alpha{i}}+\sum_{\alpha{j}}{a}^{2}_{\alpha{j}}}

The expression is minimized if we choose as $\mid {\alpha {\big \rangle }}$ the M eigenstates which belong to the M largest eigenvalues $\lambda _{\alpha }$ , $1\leq \alpha \leq {M}$ , of the reduced density matrix

$\rho _{ii'}=\sum _{j}\psi _{ij}\psi _{i'j}$

which is the projection of the ground state of B on the subsystem A'.

Correlation Functions

1. Initialization: O is on site i. When site i is added to A, $<n\mid O\mid n'>$ for site states $\mid n>$ is evaluated. $\mid {\overset {\sim }{m}}>$ are the M states of block A plus site i, $\mid m>$ those of A. Then

$<{\overset {\sim }{m}}\mid O\mid {\overset {\sim }{m}}'>=\sum _{mm'nn'}<{\overset {\sim }{m}}\mid mn><n\mid O\mid n'><m'n'\mid {\overset {\sim }{m}}'>$

2. Update: Using that O does not depend on the new site states $\mid n>$ leads to the update

$<{\overset {\sim }{m}}\mid O\mid {\overset {\sim }{m}}'>=\sum _{mm'n}<{\overset {\sim }{m}}\mid mn><m\mid O\mid m'><m'n\mid {\overset {\sim }{m}}'>$

3. Evaluation: At the final length, states $\mid m_{L}>$ and $\mid m_{R}>$ form the reduced Hilbert space of the left and right chain halves. Insertion of 1 yields $<0\mid O_{L}O_{R}\mid 0>=\sum _{m_{L}m_{R}m'_{L}m'_{R}}<0\mid m_{L}m_{R}><m_{L}\mid O_{L}\mid m'_{L}>\times <m_{R}\mid O_{R}\mid m'_{R}><m'_{L}m'_{R}\mid 0>$

where $\mid 0>$ is the ground state.