Solution to Set 5

I have no idea what I'm doing - KimberlyWynne 03:11, 2 March 2009 (EST)

Diatomic harmonic chain

Problem 1

I found this site somewhat helpful and explanatory:

http://newton.ex.ac.uk/teaching/resources/rjh/phy2009/PHY2009handout13.pdf

Given

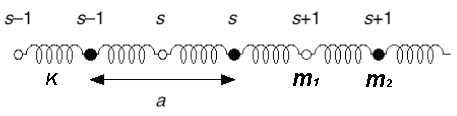
• a chain of atoms
• with alternating masses $m_{1}\;$ and $m_{2}\;$
• connected with elastic springs with constant $K\;$
• moving only in the x-direction

Derive the dispersion relation $\omega ^{\alpha }(k)\;$ for this chain

Equations of motion

$m_{1}{\ddot {u}}_{n}=-k_{1}[2u_{n}-v_{n}-v_{n-1}]\;$

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_2 \ddot{v}_n = - k_2 [2v_n - u_{n} - u_{n+1}] \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_n = u \mathrm{exp}(i(kna-\omega t))\;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_n = v \mathrm{exp}(i(kna-\omega t))\;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega^2 m u \mathrm{exp}(i(kna-\omega t)) = k (v\mathrm{exp}(i(kna-\omega t)) + v\mathrm{exp}(i(k(n-1)a-\omega t)) - 2 u \mathrm{exp}(i(kna-\omega t))) \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega^2 m_1 u = k (v + v\mathrm{exp}(-ika)) - 2 k u \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega^2 m_2 v = k (u\mathrm{exp}(ika) + u) - 2 k v \;}

Set determinant to 0

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega^2 = k(\frac{m_1+m_2}{m_1 m_2}) \pm k\sqrt{(\frac{m_1 + m_2}{m_1 m_2})^2 - \frac{4}{m_1 m_2} sin^2(\frac{ka}{2})]} \;}

Step 1:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{vmatrix} 2k-m_1\omega^2 & -C[1-\mathrm{exp}(-ika)]\\ -C[1+\mathrm{exp}(-ika)] & 2k-m_2\omega^2 \end{vmatrix} =0 }

Step 2:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{vmatrix} 2k-m_1\omega^2 & -1\\ -k & 2k-m_2\omega^2 \end{vmatrix} =0 \;}

Step 3:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2k-m_1\omega^2)(2k-m_2\omega^2)- k(1)(-k) =0 \;}

Problem 2

Determine the speed of sound for this chain. What is the lowest frequency of long-wavelength sound corresponding to the optical branch?

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega _{\alpha }(k)\approx C_{\alpha } k \;}

where

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{\alpha } \;} = frequency
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\alpha } \;} = speed of sound
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \;} = ???

Problem 3

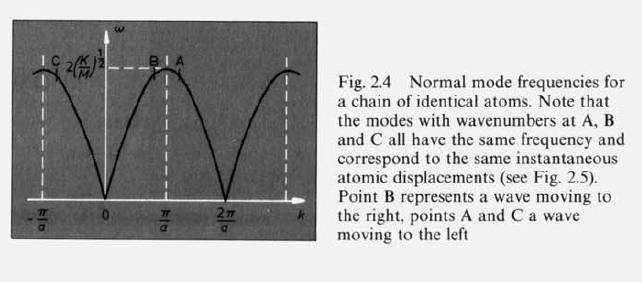
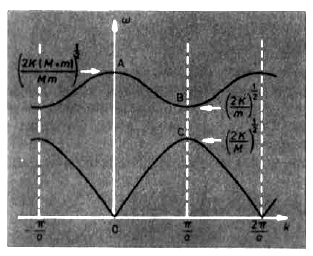
Sketch the motion of the atoms corresponding to the edge of the Brillouin zone, both for the optical and the acoustic branch.

• Acoustic Branch: lower branch
• Optical Branch: upper branch, as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \rightarrow 0 } on this branch the vibrations of the 2 types of atom are in antiphase and the resulting charge oscillation in an ionic craystal give a strong coupling to electromagnetic waves at the frequency of point A.

Problem 4

Determine the Debye temperature for this system, and determine the form of the specific heat Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_V (T)} in the limits of high and low temperatures.

Debye Temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_D \;}

The Debye temperature, aka the effective sonic velocity, is a measure of the hardness of the crystal

From our class lectures:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B T_D = \hbar \omega_D = \hbar c k_D \;}

From Wikipedia:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_D\ \stackrel{\mathrm{def}}{=}\ {hc_sR\over2Lk} = {hc_s\over2Lk}\sqrt[3]{6N\over\pi} = {hc_s\over2k}\sqrt[3]{{6\over\pi}{N\over V}}}

Specific Heat Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_V \;}

Low Temperature Limit

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{C_V}{Nk} \sim {12\pi^4\over5} \left({T\over T_D}\right)^3}

High Temperature Limit

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{high} >> \frac{\hbar\omega}{k_B} \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar\omega}{k_B T} << 1 \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\frac{\hbar\omega}{k_B T}} \approx 1 + \frac{\hbar\omega}{k_B T} + (\frac{\hbar\omega}{k_B T})^2 \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{C_V}{Nk} \sim 3\, }

Net Result (Classical Limit)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_V \approx k_B \;}

Problem 5

Consider low temperatures ($T\ll T_{D}\;$) and determine the wavelength of the most abundant phonons $\lambda _{max}$

Given

• Bose-Einstein Distribution $f(E)={\frac {1}{e^{E/k_{B}T}-1}}\;$
  • $f(E)\;$ = probability that a particle will have energy E
  • $k_{B}\;$ = Boltzmann constant
  • $T\;$ = Temperature

• Planck's Radiation Formula $E={\frac {h\omega }{e^{h\omega /k_{B}T}-1}}\;$
  • Density by frequency: $\rho (\omega )={\frac {dn_{s}}{d\omega }}={\frac {8\pi }{c^{3}}}\omega ^{2}\;$
  • Density by wavelength: $\rho (\lambda )={\frac {dn_{s}}{d\lambda }}={\frac {8\pi }{\lambda ^{4}}}\;$

• Wien's law $\lambda _{\mathrm {max} }={\frac {b}{T}}\;$
  • $\lambda _{m}ax\;$ is the peak wavelength in meters,
  • $T\;$ = temperature of the blackbody in Kelvin
  • $b\;$ = Wien's displacement constant