PHZ3400 Midterm Two Solution
PHZ 3400 – Midterm Two Exam (with solutions) – April 10, 2009
Problem 1
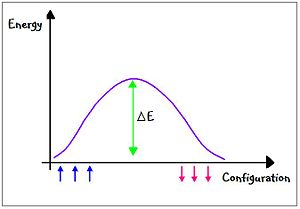
Explain the concept of the "Thermodynamic Limit", and present the corresponding domain wall argument (derivation of a formula) to estimate the relaxation time as a function of system size, at T < Tc.
The partition function which applies in this case is where n = the number of particles.
However, symmetry breaking, including phase transitions, cannot occur for any finite system[1]. Thus systems must be sufficiently large, , in order to reach the thermodynamic limit and for spontaneous symmetry breaking to occur.
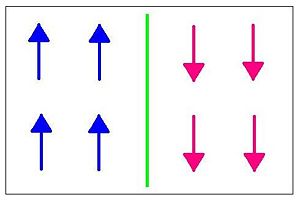
Suppose we start in a system where all of the spins are up and we would like to make them spin down. This can be done by applying a domain wall to the system.
[1] [http://prola.aps.org/abstract/PR/v87/i3/p404_1
C. N. Yang and T. D. Lee, Statistical Theory of Equations of State and Phase Transitions. I. Theory of Condensation Phys. Rev. 87, 404 - 409 (1952)]
Problem 2
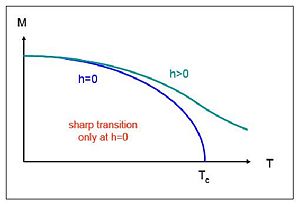
Sketch the magnetization of a ferromagnet as a function of temperature T, for (A) Zero external magnetic field and (B) Finite external magnetic field. How is the behavior around the Curie Temperature (Tc) affected by the field?
(A) For zero external magnetic field, the magnetization of a ferromagnet as a function of temperature T should go through the Curie Temperature (Tc). The Tc will be unique based on the ferromagnet.
Problem 3
Problem 4
Consider a neutron star of radius R = 10km, and mass M = 3x10^30 kg (approximately 1.5 solar masses). Given that the mass of a single neutron is m=1.7*10^-27 kg, that h-bar = 1x10^-34 m^2 kg/s, and that neutrons obey Fermi-Dirac Statistics, calculate:
a. The number density n=N/V of this star. N = total number of objects in volume V. Using this, we first can find the volume of the neutron star.
b. Derive in detail the relation between Fermi energy and the number density.
- .
For a 3-D object,
where the factor 2 comes from the fact that there are 2 spin states, 1/8 comes from the fact that only 1/8 of the sphere is positive, and comes from the volume of the sphere with radius
Solving for and then substituting into yields
and then finally