PHZ3400 Midterm Two Solution

PHZ 3400 – Midterm Two Exam (with solutions) – April 10, 2009

Problem 1

Explain the concept of the "Thermodynamic Limit", and present the corresponding domain wall argument (derivation of a formula) to estimate the relaxation time as a function of system size, at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T < T_c} .

Canonical partition function

Given a thermodynamically large system that is in constant thermal contact with the environment, where both the volume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} and the number of constituent particles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} are fixed. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} = 1, 2, 3, ...) are the exact states (microstates) that the system can occupy, generally, these can be regarded as discrete quantum states of the system.

Therefore, the canonical partition function is defined as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z = \sum_{n}^{\infty} e^{-\beta E_n} \;}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z \;} = statistical function of Temperature

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e \;} = base of the natural logarithm

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = \tfrac{1}{k_{B}T} \;} = the inverse temperature where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B} is the Boltzmann const

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n} \;} = total energy of the system

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \;} = the number of particles.

Thermodynamic Limit

Spontaneous symmetry breaking (i.e. phase transitions) cannot occur for a finite system . There must be an infinite number of spins. Thus systems must be sufficiently large, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta \rightarrow \infty \;} , in order to reach the thermodynamic limit and for spontaneous symmetry breaking to occur.

I still don't know what this is. What is it defined as? The limit of the number of spins as it goes to infinity:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\eta \rightarrow \infty } \;}  ? The temperature at which spontaneous symmetry breaking can occur? The point where the domain wall begins? KimberlyWynne 00:25, 16 April 2009 (EDT)

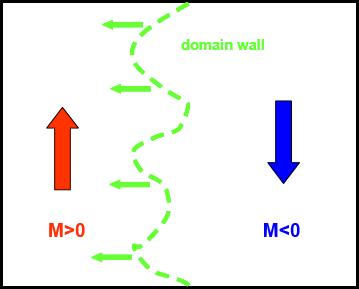
Domain Wall Argument

A domain wall is an interface transition of 180° angular displacements on magnetic spin.

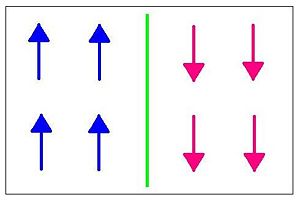
Given a ferromagnetic system where all of the spins are up at t = 0, and we want to find the time t it takes to reverse them to all spin down. The energetically easiest way to do this would be to "push" a domain wall through the system.

This illustrates the most energetically favorable configuration of the system. The green line represents the Domain Wall.

Derivation

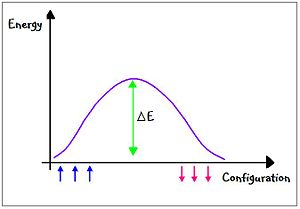
This can be further described by this image, which shows the probability of the system being in those states. Notice that the image shows the system is most likely to be found in a state where there is a mix of up and down spins. The domain wall will, by its nature, try to find the most energetically favorable state and it will thus lie where the energy of the probability of the states of the system is at a maximum.

This illustrates the probability of states. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta E} is the energy of the Domain Wall

Probability

The probability of reaching the all-spin-down configuration

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E)\propto e^{-\tfrac{E}{k_{B}T}} = e^{-\beta E} \;}

When there is random motion, the probability is proportional to time

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E)\propto T \;} .

Since we are dealing with a domain wall, we can replace E with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta E} from the illustration, which is also defined as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta E = \delta L^{d-1} \;}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta\;} = surface tension Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \propto J} - the interaction between spins

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L\; } = system size

With this substitution, we get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(E) \propto e^{-\beta \Delta E} \propto \tau \propto e^{-A \tfrac{L^{d-1}}{T}}} .

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \;} = dummy variable representing some constant

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \;} = dimension, so for a 3-dimensional case we get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^{3-1} = L^{2}} .

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \;} = relaxation time

Therefore, the equation gives a relationship between the relaxation time and the size of the system.

Relaxation time

The relaxation time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \;} and the size of the system have a direct correlation. As the size of the system increases the relaxation time also increases, albeit at a greater rate. Thus if the size of the system is very large (macroscopic objects) then the relaxation time becomes larger than the age of the universe, and the system will stay in its current state.

Another interesting relation is between the relaxation time and temperature. As the temperature gets lower, the relaxation time gets larger. This fits in well with superconductors since they are only conducting at low temperatures. This means that as the semiconductors cool down the spins align and exhibit symmetry breaking.

Problem 2

Sketch the magnetization of a ferromagnet as a function of temperature T, for (A) Zero external magnetic field and (B) Finite external magnetic field. How is the behavior around the Curie Temperature (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} ) affected by the field?

(A) Zero External Magnetic field

For zero external magnetic field, the magnetization of a ferromagnet as a function of temperature T should go zero at the Curie Temperature (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} ). The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} will be unique based on the ferromagnet. The image below illustrates this behavior.

Ignore the temperature but observe the trend as the magnetization approaches 0 at the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} . Image is from [2]

(B) Finite External Magnetic Field

When there is an external magnetic field, the magnetism does not drop to zero at the Curie temperature. Rather, the magnetization of the ferromagnet will trail off as shown by the teal line in the image below.

This image shows the results for zero external magnetic field(blue) overlayed with the results with an external magnetic field(teal). Image from Dr. Dobrosavljevic's notes [3]

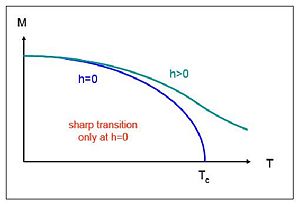
Behavior around the Curie Temperature

Even though the curie temperature is unique to each magnet, the behavior at the Curie point is similar for all of them. When the magnet reaches its Curie temperature, the spins lose their alignment and become randomly oriented. This prevents a magnetic field from forming. For superconductors, the curie temperature is very low, which is why they are non-conducting at room temperature.

Problem 3

Consider a solid with vibrations well described by the "Einstein Model", where a single vibrational frequency Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0} is considered. [Note: Phonons obey Bose-Einstein statistics.]

Bose-Einstein Distribution

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta _{phonon} = \frac{1}{e^{\tfrac{\hbar \omega}{kT}}-1}\;}

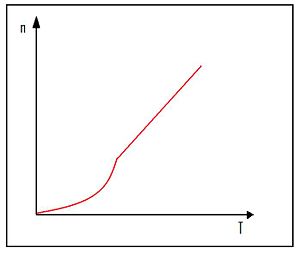
(A) Density as a function of T

What is the density of phonons with this frequency as a function of the temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} ? Sketch this function.

This image represents the photon density n as a function of the temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T}

(B) Density at Low Temperatures

What is the phonon density at very low temperatures?

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{T \to 0} \eta (T) = \lim_{T \to 0} \frac{1}{e^{\tfrac{\hbar \omega}{kT}}-1}\;}

However, as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\to0 } 'e' becomes very large, disregard the 1, thus the equation becomes:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n(T) = e^{-\tfrac{ \hbar \omega}{kT} } \;}

(C) Density at High Temperatures

What is the phonon density at very high temperatures?

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{T \to \infty } \eta (T) = \lim_{T \to \infty } \frac{1}{e^{\tfrac{\hbar \omega}{kT}}-1} \;}

As Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\to\infty} 'e' becomes very small and we can make a substitution such that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{- \hbar \omega / kT} \sim \tfrac{1}{1 + {\tfrac{\hbar \omega}{kT}}} }

Therfore we can say that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n(T) \sim \tfrac{kT}{\hbar \omega} \sim T. }

(D) Temperature dependence of Resistivity

Assuming that the scattering rate of electrons in such a solid is simply proportional to the density of phonons, determine the temperature dependence of resistivity at high temperatures.

The Drude formula can be used to relate the resistivity and the phonon density through a few simple mathematical manipulations. The Drude formula is as follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \tfrac{ne^2 \tau}{m} }

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} = conductivity

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} = phonon density,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} = mass,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau = \tfrac{l}{v}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} = mean free path and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} = velocity.

Since resitivity ($\rho$) and conductivity ($\sigma$) are inversely proportional, we can write that

${\tfrac {1}{\sigma }}=\rho ={\tfrac {m}{ne^{2}\tau }}$

Now when $n(T)\sim {\tfrac {1}{\tau }}$, it is also proportional to T.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n(T) \propto T}

Thus when written together we have:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau ^{-1} \sim \eta(T) \sim T = \frac{1}{\delta } = \frac{m}{\eta e^2 \tau} \;}

Problem 4

Consider a neutron star of radius R = 10km, and mass M = 3x10³⁰ kg (approximately 1.5 solar masses). Given that the mass of a single neutron is m=1.7*10^-27 kg, that h-bar = 1x10^-34 m² kg/s, and that neutrons obey Fermi-Dirac Statistics, calculate:

(A) Number Density

Calculate the number density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \frac{N}{V}} of this star.

N = total number of objects and V = volume. We can begin by calculating the volume of the neutron star.

Assuming that the neutron star is spherical:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V =\frac{4}{3} \pi R^3 }

We are given that the radius is 10km which is equal to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1x10^4} m. Plugging this in:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V =\frac{4}{3} \pi (1x10^4m)^3 = 4.189x10^{12}m^3}

Now we can calculate N:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = \frac{M}{m}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M = 3x10^{30}kg} = mass of the neutron star and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m = 1.7x10^{-27}kg} = mass of a single neutron. Plugging in we get the following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = \frac{M}{m} = \frac{3x10^{30}kg}{1.7x10^{-27}kg} = 2.5x10^{57}}

Having both of these numbers, we can now calculate the number density (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} )

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \frac{N}{V} = \frac{2.5x10^{57}}{4.189x10^{12}m^3} = 5.968x10^{44}\frac{1}{m^3}}

(B) Fermi Energy and Number Density

Derive in detail (as we did in class; show all the steps) the relation between Fermi energy and the number density.

We begin this derivation by saying that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E(k) = \frac{\hbar ^2k_f^2}{2m}}

We can solve this for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_f} such that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F = \sqrt{ \frac{2mE_f}{\hbar ^2}}}

We are attempting to derive the relation between the Fermi energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_f} and the number density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} . Keeping in mind that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \frac {N}{V}} , that there is a coefficient of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2} due to spin, and that there is a variable L which is controlled by te dimension we are working in, we can represent Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} as a sum over k.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n =\frac{2}{L^3} \sum_{k < |k_F|}^{} } .

We would like to turn this sum into an integral, so we must first define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta k} which will become Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dk} in our integral.

As mentioned before, we are working in three dimensions so we can set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta k = (\frac{2\pi}{L})^3} .

We know that we can multiply anything by one, so we now multiply by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\Delta k}{\Delta k}} such that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n =\frac{2}{L^3} \sum_{k < |k_f|}^{} (\frac{2\pi}{L})^3 (\frac{L}{2\pi})^3} .

Now we can set this equal to an integral

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n =\frac{2}{L^3} \sum_{k < |k_f|} (\frac{2\pi}{L})^3 (\frac{L}{2\pi})^3 = \frac{1}{4\pi ^3}\int dk}

We need to change this integral into spherical coordinates to account for the dimensions. This changes the integral into

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\pi ^2}\int dk k^2 }

Putting this all together we get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n =\frac{2}{L^3} \sum_{k < |k_f|} (\frac{2\pi}{L})^3 (\frac{L}{2\pi})^3 = \frac{1}{4\pi ^3}\int d^3 k \rightarrow \frac{1}{\pi ^2}\int_0^{k_F} k^2 dk = \frac{1}{\pi ^2} \frac{1}{3}k_F^3 = \frac{k_F^3}{3\pi ^2}}

So Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \frac{k_F^3}{3\pi ^2}}

and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F = (3\pi n)^{1/3} \;}

Thus plugging back into the formula we started with we get that the Fermi Energy is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_F(k) = \frac{\hbar ^2}{2m}(3\pi^2 n)^{2/3} }

(C) Value of Fermi Energy

Estimate the Fermi energy of this neutron star in Joules.

Begin with the given equation of Fermi Energy:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_F = \tfrac{\hbar ^2}{2m}(\tfrac{3\pi ^2N}{V})^{2/3}} .

Since in part (A) we solved for the number density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \frac{N}{V}} , substitute Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{N}{V}} with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\;} to get:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_F = \tfrac{\hbar ^2}{2m}(3\pi ^2n)^{2/3}}

Now we can plug in all the variables such that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_F = \tfrac{(1 \times 10^{-34}\tfrac{m^2kg}{s}) ^2}{2(1.7 \times 10^{-27}kg)}(3 \pi ^2 5.968 \times 10^{44}\tfrac{1}{m^2})^{2/3}} .

By completing the calculations we can find that the solution is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_F = 1.131 \times 10^{-68} \tfrac {m^2 kg}{s^2} = 1.995 \times 10^{-11} J} .

(D) Fermi Temperature

Using the fact that 1eV = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1.60217646 \times 10^{-19} } Joules, and that 1meV ~ 10K, estimate the Fermi temperature of this neutron star. How does it compare to that of a typical nucleus, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_f ~ 30MeV} ?

Using what we calculated in part (D), we can now compute the unit change from J to eV and from eV to meV.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1.13x10^{-11}J}{} \frac{1eV}{1.60217646x10^{-19}J} \frac {1000meV}{1eV} = 1.245x10^{11}meV }

Since we know that 1meV ~ 10K, we can then multiply our Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_f} value by 10 and we get that the Fermi temperature of this neutron star is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1.245x10^{12} K } .

In MeV, the the Fermi Energy is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_f = 124.5MeV} .

This is very much greater than that of a typical nucleus which has a Fermi Energy of

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_f ~ 30MeV} .

(E) Temperature Comparison

Given that the typical temperature of this neutron star is T ~ $10^{6}$ K, is this neutron star "cool" or is it "hot"(as compared to the Fermi temperature)?

It is hot.

This neutron star has a $T_{f}$ ~ $10^{12}$ K which is several orders of magnitude greater than the temperature of a typical neutron star which has a temperature of T ~ $10^{6}$ K.