Phy5646
Welcome to the Quantum Mechanics B PHY5646 Spring 2009
This is the second semester of a two-semester graduate level sequence, the first being PHY5645 Quantum A. Its goal is to explain the concepts and mathematical methods of Quantum Mechanics, and to prepare a student to solve quantum mechanics problems arising in different physical applications. The emphasis of the courses is equally on conceptual grasp of the subject as well as on problem solving. This sequence of courses builds the foundation for more advanced courses and graduate research in experimental or theoretical physics.
The key component of the course is the collaborative student contribution to the course Wiki-textbook. Each team of students (see Phy5646 wiki-groups) is responsible for BOTH writing the assigned chapter AND editing chapters of others.
This course's website can be found here.
Team assignments: Spring 2010 student teams
Outline of the course:
Stationary state perturbation theory in Quantum Mechanics
Very often, quantum mechanical problems cannot be solved exactly. An approximate technique can be very useful since it gives us quantitative insight into a larger class of problems which do not admit exact solutions. One technique is the WKB approximation, which holds in the asymptotic limit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar\rightarrow 0 } .
Perturbation theory is another very useful technique, which is also approximate, and attempts to find corrections to exact solutions in powers of the terms in the Hamiltonian which render the problem insolvable. The basic idea of perturbation theory deals with the notion of continuity such that you must be able to write the given Hamiltonian in a way that involves the solvable part of the Hamiltonian with very small additional terms that represent the insolvable parts. In the case of non-degenerate perturbation theory the following assumption must hold: both the energy and the wavefunctions of the insolvable Hamiltonian have analytic expansion in powers of the real parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} -- to insure no jump discontinuities -- equals zero where the perturbing term is taken to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda\mathcal{H}'} . The quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} , which is taken to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 < \lambda < 1 } , has no physical significance, and is merely used as a way to keep track of order.
The Hamiltonian is taken to have the following structure:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}=\mathcal{H}_0+\lambda\mathcal{H}'}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_0} is exactly solvable and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}'} makes it insolvable by analytical methods. Therefore the eigenvalue problem becomes:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\mathcal{H}_0+\lambda\mathcal{H}')|\psi> = E_n|\psi> }
At the end of the calculation we set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=1} .
It is important to note that perturbation theory tends to yield fairly accurate energies, but usually yields very poor wavefunctions.
Rayleigh-Schrödinger Perturbation Theory
We begin with an unperturbed problem, whose solution is known exactly. That is, for the unperturbed Hamiltonian, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_0} , we have eigenstates, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle } , and eigenenergies, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal \epsilon_n } , that are known solutions to the Schrodinger equation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_0 |n\rangle = \epsilon_n |n\rangle \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad (1.1.1) }
To find the solution to the perturbed hamiltonian, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}}
, we first consider an auxiliary problem, parameterized by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal \lambda}
:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = \mathcal{H}_0 + \lambda \mathcal{H}^' \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad (1.1.2) }
The only reason for doing this is that we can now, via the parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} , expand the solution in powers of the component of the hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}'} , which is presumed to be relatively small in comparison with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_0} . In nature we do not know a priori that this will work, and choosing the correct perturbation for a particular problem will likely require some insight into the problem or by a numerical solution.
We attempt to find eigenstates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |N(\lambda)\rangle} and eigenvalues Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n} of the Hermitian operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , and assume that they can be expanded in a power series of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal\lambda} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n(\lambda) = E_n^{(0)} + \lambda E_n^{(1)} + ... + \lambda^j E_n^{(j)} + ... }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |N(\lambda)\rangle = |\Psi_n^{(0)}\rangle + \lambda|\Psi_n^{(1)}\rangle + \lambda^2 |\Psi_n^{(2)}\rangle + ... \lambda^j |\Psi_n^{(j)}\rangle + ... \qquad\qquad\qquad\qquad\qquad\;\;\;\;\;\; (1.1.3)}
Where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi_n^{(j)}\rangle} signify the j-th order correction to the unperturbed eigenstate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle} , upon perturbation. Then we must have,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} |N(\lambda)\rangle = E(\lambda) |N(\lambda)\rangle \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;\;\;\; (1.1.4)}
Which upon expansion, becomes: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\mathcal{H}_0 + \lambda \mathcal{H}')\left(\sum_{j=0}^{\infty}\lambda^j |\Psi_n^{(j)}\rangle \right) = \left(\sum_{l=0}^{\infty} \lambda^l E_n^{(l)}\right)\left(\sum_{j=0}^{\infty}\lambda^j |\Psi_n^{(j)}\rangle \right) \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;\; (1.1.5)}
In order for this method to be useful, the perturbed energies must vary continuously with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} . Knowing this we can see several things about our as yet undetermined perturbed energies and eigenstates. For one, as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda \rightarrow 0, |N(\lambda)\rangle \rightarrow |\Psi_n^{(0)}\rangle = |n\rangle} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n(\lambda) \rightarrow E_n^{(0)} = \epsilon_n} for some unperturbed state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle} .
For convenience, assume that the unperturbed states are already normalized: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n | n \rangle = 1} , and choose normalization such that the exact states satisfy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n|N(\lambda)\rangle=1} . Then in general Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |N\rangle} will not be normalized, and we must normalize it after we have found the states (see Phy5646#Renormalization).
Thus, we have:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n|N(\lambda)\rangle= 1 = \langle n |\Psi_n^{(0)}\rangle + \lambda \langle n |\Psi_n^{(1)}\rangle + \lambda^2 \langle n |\Psi_n^{(2)}\rangle + ... \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;\;\;\;(1.1.6)}
Coefficients of the powers of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} must match, so,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n | \Psi_n^{(i)} \rangle = 0, i = 1, 2, 3, ... \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;(1.1.7)}
Which shows that, if we start with the unperturbed state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle }
, upon perturbation, then we add to this initial state a set of perturbation states, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi_n^{(0)}\rangle, |\Psi_n^{(1)}\rangle, ... }
which are all orthogonal to the original state -- so the unperturbed states become mixed together.
We equate coefficients in the above expanded form of the perturbed Hamiltonian (eq. #1.1.5), we are provided with the corrected eigenvalues for whichever order of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda}
we want. The first few are as follows,
0th Order Energy
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda^0 \rightarrow E_n^{(0)} = \epsilon_n \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (1.1.8)}
which we already had before.
1st Order Energy Corrections Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda^1 \rightarrow \mathcal{H}_0 |\Psi_n^{(1)}\rangle + \mathcal{H}' |\Psi_n^{(0)}\rangle = E_n^{(1)} |\Psi_n^{(0)}\rangle + E_n^{(0)} |\Psi_n^{(1)}\rangle } , taking the scalar product of this result of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle} , and using our previous results, we get: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n^{(1)} = \langle n|\mathcal{H}'|n\rangle \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;\;(1.1.9)}
2nd Order Energy Corrections
Taking the terms in eq #1.1.5 that are second order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} and operating on them with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle} provides us with up to the second order:
One interesting thing to note about this is that is positive definite. Therefore, since , the second order energy correction will always lower the ground state energy.
kth order Energy Corrections In general,
This result provides us with a recursive relation for the eigenenergies of the perturbed state, so that we have access to the eigenenergies for an state of arbitrary order in .
What about the eigenstates? Express the perturbed states in terms of the unperturbed states:
Go back to equation #1.1.5 and take the scalar product from the left with and then, compare orders of to find:
1st order Eigenkets
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle m|\Psi_n^{(1)}\rangle = \frac{\langle m | n\rangle}{\epsilon_n - \epsilon_m}}
The first order contribution is then the sum of this equation over all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} , and adding the zeroth order we get the eigenstates of the perturbed hamiltonian to the 1st order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |N\rangle = |n\rangle + \lambda\sum_{k \not= n} |m\rangle \frac{\langle m |V| n\rangle}{\epsilon_n - \epsilon_m} + ...\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;\;(1.1.11)}
Going beyond order one in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} gets increasingly messy, but can be done by the same procedure.
Renormalization
Earlier we assumed that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n|N(\lambda)\rangle=1} , which means that our Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |N(\lambda)\rangle} states are not normalized themselves. To reconcile this we introduce the normalized perturbed eigenstates, denoted Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{N}} . These will then be related to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\lambda)} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\bar{N}\rangle = \frac{|N\rangle}{\sqrt{\langle N|N\rangle}} =z^{1/2}|N\rangle \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(1.1.12)}
Thus Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} gives us a measure of how close the perturbed state is to the original state.
To second order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{z (\lambda )} = \langle N(\lambda )|N(\lambda )\rangle = ( \langle n| + \lambda \langle\Psi_n^{(1)}| + ...)( \langle n| + \lambda \langle\Psi_n^{(1)}| + ...)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z(\lambda ) = \frac{1}{1 + \lambda^2\sum_{ n \not= m}\frac{|\langle m|V|n\rangle|^2}{(\epsilon_n - \epsilon_m)^2} + ...} = 1 - \lambda^2\sum_{ n \not= m}\frac{|\langle m|V|n\rangle|^2}{(\epsilon_n - \epsilon_m)^2} + ... \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;\;\;\;\;(1.1.14)}
Where we use a taylor expansion to arrive at the final result (noting that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{|\langle m|V|n\rangle|^2}{(\epsilon_n - \epsilon_m)^2} < 1} ).
Then, interestingly, we can show that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle} is related to the energies by employing equation 1.1.10:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z(\lambda ) = \frac{\partial E_n}{\partial \epsilon_n}\Big|_{\epsilon_m}{\langle m|V|n\rangle} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;(1.1.15)}
Where the derivative is taken with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_n} , while holding Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle m|V|n\rangle} constant. Using the Brillouin-Wigner perturbation theory (see next section) it can supposedly be shown that this relation holds exactly, without approximation.
Problem examples of non-degenerate perturbation theory :
-Problem 1: demonstrating how linear algebra can be used to solve for the exact eigenstates, exact eigenevalues, first and second order corrections to the eigenvalues, and first order corrections to the eigenstates of a given Hamiltonian
Brillouin-Wigner Perturbation Theory
Brillouin-Wigner perturbation theory is an alternative perturbation method based on treating the right hand side of
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (E_n - H_0)|N\rangle = H'|N\rangle }
as a known quantity. This method is not strictly an expansion in lambda.
Using a basic formula derived from the Schrodinger equation, you can find an approximation for any power of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda } required using an iterative process. This theory is less widely used as compared to the RS theory. At first order the two theories are equivalent. However,the BW theory extends more easily to higher order and avoid the need for separate treatment of non degenerate and degenerate levels. In addition, if we have a good approximation for the value of , the BW series should converge more rapidly than the RS series.
Starting with the Schrodinger equation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} ({\mathcal H}_o+\lambda {\mathcal H}')|N\rangle &= E_n|N\rangle \\ \lambda {\mathcal H}'|N\rangle &= (E_n-{\mathcal H}_o)|N\rangle \\ \langle n|(\lambda {\mathcal H}'|N\rangle) &= \langle n|(E_n-{\mathcal H}_o)|N\rangle \\ \lambda \langle n|{\mathcal H}'|N\rangle &= (E_n-\epsilon_n)\langle n|N\rangle \\ \end{align} }
If we choose to normalize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n|N \rangle = 1 } , then so far we have: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (E_n-\epsilon_n) = \lambda\langle n|{\mathcal H}'|N\rangle \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\; (1.2.1)}
which is still an exact expression (no approximation have been made yet). The wavefunction we are interested in, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |N\rangle } can be rewritten as a summation of the eigenstates of the (unperturbed, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal H}_o } ) Hamiltonian: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |N\rangle &= \sum_m|m\rangle\langle m|N\rangle\\ &= |n\rangle\langle n|N\rangle + \sum_{m\neq n}|m\rangle\langle m|N\rangle\\ &= |n\rangle + \sum_{m\neq n}|m\rangle\frac{\lambda\langle m|{\mathcal H}'|N\rangle}{(E_n-\epsilon_m)}\\ \end{align} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;\;\;\; (1.2.2)}
The last step has been obtained by using eq #1.2.1. So now we have a recursive relationship for both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n } and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n = \epsilon_n+\lambda\langle n|{\mathcal H}'|N\rangle } where can be written recursively to any order of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda } desired
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |N\rangle = |n\rangle+\lambda \sum_{m\neq n}|m\rangle\frac{\lambda\langle m|{\mathcal H}'|N\rangle}{(E_n-\epsilon_m)} } where can be written recursively to any order of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda } desired
For example, the expression for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |N\rangle } to a third order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda } would be:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |N\rangle &= |n\rangle + \lambda\sum_{m\neq n}|m\rangle\frac{\langle m|{\mathcal H}'}{(E_n-\epsilon_m)}\left(|n\rangle + \lambda\sum_{j\neq n}|j\rangle\frac{\langle j|{\mathcal H}'}{(E_n-\epsilon_j)}\left(|n\rangle + \lambda\sum_{k\neq n}|k\rangle\frac{\langle k|{\mathcal H}'|n\rangle}{(E_n-\epsilon_k)}\right)\right)\\ &= |n\rangle + \lambda\sum_{m\neq n}|m\rangle\frac{\langle m|{\mathcal H}'|n\rangle}{(E_n-\epsilon_m)} + \lambda^2\sum_{m,j\neq n}|m\rangle\frac{\langle m|{\mathcal H}'|j\rangle\langle j|{\mathcal H}'|n\rangle}{(E_n-\epsilon_m)(E_n-\epsilon_j)} + \lambda^3\sum_{m,j,k\neq n}|m\rangle\frac{\langle m|{\mathcal H}'|j\rangle\langle j|{\mathcal H}'|k\rangle\langle k|{\mathcal H}'|n\rangle}{(E_n-\epsilon_m)(E_n-\epsilon_j)(E_n-\epsilon_k)}\\ \end{align} } ,
where is unity.
Note that we have chosen Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n|N \rangle = 1} , i.e. the correction is perpendicular to the unperturbed state. That is why at this point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |N \rangle} is not normalized. The normalized wave function can be written as
Interestingly, the normalization constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z} turns out be exactly equal to the derivative of the exact energy with respect to the unperturbed energy, ie
The calculation for the normalization constant can be found through this link.
We can expand #1.2.1 with the help of #1.2.2, this gives:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n = \epsilon_n + \lambda\langle n|H'|n\rangle + \lambda^2\sum ' \frac{|\langle m|H'|n\rangle|^2}{E_n - \epsilon_m} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\;\; (1.2.3)} .
Notice that if we replaced with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_n} we would recover the Raleigh-Schrodinger perturbation theory. By itself #1.2.2 provides a transcendental equation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n} , since appears in the denominator of the right hand side. If we have some idea of the value of a particular Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n} , then we could use this as a numerical method to iteratively get better and better values for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n} .
Degenerate Perturbation Theory
Degenerate perturbation theory is an extension of standard perturbation theory which allows us to handle systems where one or more states of the system have non-distinct energies. Normal perturbation theory fails in these cases because the denominators of the expressions for the first-order corrected wave function and for the second-order corrected energy become zero. If more than one eigenstate for the Hamiltonian has the same energy value, the problem is said to be degenerate. If we try to get a solution using perturbation theory, we fail, since Rayleigh-Schroedinger PT includes terms like Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/\mathcal(\epsilon_n-\epsilon_m) } .
Instead of trying to use these degenerate eigenstates with perturbation theory, we start with the non-degenerate linear combinations of the original eigenstates so that regular perturbation theory may be applied. In other words, the first, and only, extra step of degenerate perturbation theory is to find linear combinations by diagonalizing the perturbation within the set of degenerate states and then proceeding as usual in non-degenerate perturbation.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{|n_a\rangle,|n_b\rangle,|n_c\rangle,\dots\} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{|n_{\alpha}\rangle,|n_{\beta}\rangle,|n_{\gamma}\rangle,\dots\} } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_{\alpha}\rangle = \sum_iC_{\alpha,i}|n_i\rangle } etc
The general procedure for doing this type of problem is to create the matrix with elements formed from the degenerate eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal H}_o } . This matrix can then be diagonalized, and the eigenstates of this matrix are the correct linear combinations to be used in non-degenerate perturbation theory. In other words, we choose to manipulate the expression for the Hamiltonian so thatFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n_\alpha|H'|n_\beta\rangle } goes to zero for all cases Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \ne \beta} . One can then apply the standard equation for the first-order energy correction, noting that the change in energy will apply to the energy states described by the new basis set. (In general, the new basis will consist of some linear superposition of the existing state vectors of the original system.)
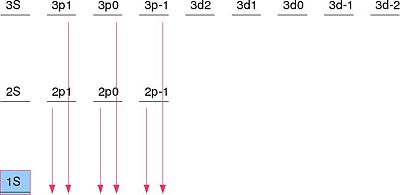
One of the well-known examples of an application of degenerate perturbation theory is the Stark Effect. If we consider a Hydrogen atom with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=2 } in the presence of an external electric field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathcal E}={\mathcal E}\hat{z} } . The Hamiltonian for this system is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal H}={\mathcal H}_o-e{\mathcal E}z } . The eigenstates of the system are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{|2S\rangle,|2P_{-1}\rangle,|2P_0\rangle,|2P_{+1}\rangle\} } . The matrix of the degenerate eigenstates and the perturbation is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle n_i|{\mathcal H}'|n_j\rangle &\longrightarrow \left(\begin{array}{cccc}\langle2S|-e{\mathcal E}z|2S\rangle&\langle2S|-e{\mathcal E}z|2P_{-1}\rangle&\langle2S|-e{\mathcal E}z|2P_0\rangle&\langle2S|-e{\mathcal E}z|2P_{+1}\rangle\\\langle2P_{-1}|-e{\mathcal E}z|2S\rangle&\langle2P_{-1}|-e{\mathcal E}z|2P_{-1}\rangle&\langle2P_{-1}|-e{\mathcal E}z|2P_0\rangle&\langle2P_{-1}|-e{\mathcal E}z|2P_{+1}\rangle\\\langle2P_0|-e{\mathcal E}z|2S\rangle&\langle2P_0|-e{\mathcal E}z|2P_{-1}\rangle&\langle2P_0|-e{\mathcal E}z|2P_0\rangle&\langle2P_0|-e{\mathcal E}z|2P_{+1}\rangle\\\langle2P_{+1}|-e{\mathcal E}z|2S\rangle&\langle2P_{+1}|-e{\mathcal E}z|2P_{-1}\rangle&\langle2P_{+1}|-e{\mathcal E}z|2P_0\rangle&\langle2P_{+1}|-e{\mathcal E}z|2P_{+1}\rangle\\\end{array}\right)\\ &\longrightarrow \left(\begin{array}{cccc}0&0&\langle2S|-e{\mathcal E}z|2P_0\rangle&0\\0&0&0&0\\\langle2P_0|-e{\mathcal E}z|2S\rangle&0&0&0\\0&0&0&0\\\end{array}\right)\\ &\longrightarrow \left(\begin{array}{cccc}0&0&-3e{\mathcal E}a_B&0\\0&0&0&0\\-3e{\mathcal E}a_B&0&0&0\\0&0&0&0\\\end{array}\right)\\ \end{align} }
To briefly summarize how most of the terms in this matrix work out to be zero (the full arguments as to how most of these terms are zero is worked out in G Baym's "Lectures on Quantum Mechanics" in the section on Degenerate Perturbation Theory) first note that the hydrogen atom is degenerate under parity, and as a result, all the elements on the diagonal become zero. The other elements vanish because of angular momentum. Matrix elements of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda } V between states with different eigenvalues of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{z}} vanish, since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e{\mathcal E}z } commutes with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{z} } . For example,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 = \langle 2P_{-1}| [e{\mathcal E}z, L_{z} ] | 2P_{1} \rangle = \langle 2P_{-1} | e{\mathcal E}z (L_{z}|P_{1} \rangle) -( \langle 2P_{-1}|L_{z}) e{\mathcal E}z|2P_{1} \rangle = 2\hbar \langle 2P_{-1}|e {\mathcal E}z|2P_{1} \rangle } which means that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle 2P_{-1}|e {\mathcal E}z| 2P_{1} \rangle = 0 }
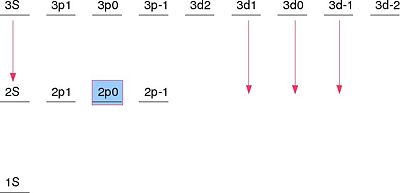
The correct linear combination of the degenerate eigenstates ends up being
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{|2P_{-1}\rangle,|2P_{+1}\rangle,\frac{1}{\sqrt{2}}\left(|2S\rangle+|2P_0\rangle\right),\frac{1}{\sqrt{2}}\left(|2S\rangle-|2P_0\rangle\right)\} }
Because of the perturbation due to the electric field, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |2P_{-1}\rangle } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |2P_{+1}\rangle } states will be unaffected. However, the energy of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |2S\rangle } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |2P_0\rangle } states will have a shift due to the electric field.
Example: 1D harmonic oscillator
Consider 1D harmonic oscillator perturbed by a constant force.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = -F\mathbf{x}}
The energy up to second order is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n}=\epsilon_{n}+\langle n|V|n\rangle +\sum_{m\neq n} \frac{|\langle m|V|n\rangle |^{2}}{\epsilon_{n}-\epsilon_{m}} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (1.3.1) }
Let's see the matrix elements
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle m|V|n\rangle &=-F\langle m|\mathbf{x}|n\rangle\\ &=-F\langle m|\sqrt{\frac{\hbar}{2m\omega}}\left( \mathbf{a}+\mathbf{a}^{\dagger}\right)|n\rangle\\ &=-F\sqrt{\frac{\hbar}{2m\omega}}\left( \langle m|\mathbf{a}|n\rangle+\langle m|\mathbf{a}^{\dagger}|n\rangle\right)\\ &=-F\sqrt{\frac{\hbar}{2m\omega}}\left( \sqrt{n}\langle m|n-1\rangle+\sqrt{n+1}\langle m|n+1\rangle\right)\\ &=-F\sqrt{\frac{\hbar}{2m\omega}}\left( \sqrt{n}\delta_{m,n-1}+\sqrt{n+1}\delta_{m,n+1}\right)\\ \end{align}}
We see that:
- The first order term in eq. #1.3.1 is:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n|V|n\rangle=0}
- The Second order term is:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \sum_{m\neq n} \frac{|\langle m|V|n\rangle |^{2}}{\epsilon_{n}-\epsilon_{m}}&= \frac{|\langle n-1|V|n\rangle |^{2}}{\epsilon_{n}-\epsilon_{n-1}}+\frac{|\langle n+1|V|n\rangle |^{2}}{\epsilon_{n}-\epsilon_{n+1}}\\ &=\frac{|\langle n-1|V|n\rangle |^{2}}{\hbar \omega (n+\frac{1}{2})-\hbar \omega (n-1+\frac{1}{2})}+\frac{|\langle n+1|V|n\rangle |^{2}}{\hbar \omega (n+\frac{1}{2})-\hbar \omega (n+1+\frac{1}{2})}\\ &=\frac{|\langle n-1|V|n\rangle |^{2}}{\hbar \omega}+\frac{|\langle n+1|V|n\rangle |^{2}}{-\hbar \omega}\\ &=\frac{1}{\hbar \omega}\left(\frac{\hbar}{2m\omega}F^{2}n-\frac{\hbar}{2m\omega}F^{2}(n+1)\right)\\ &=\frac{-F^{2}}{2m\omega^{2}} \end{align}}
Finally the energy is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n}=\epsilon_{n}-\frac{F^{2}}{2m\omega^{2}} }
This results is exactly the same as when we solve the problem without perturbation theory.
Time dependent perturbation theory in Quantum Mechanics
Formalism
Previously, we learned time independent perturbation theory in which a little change in the Hamiltonian generates a correction in the form of a series expansion for the energy and wave functions. The problem for a time independent Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} can be solved by finding a solution to the equation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}|n\rangle = E_n|n\rangle} . And then changes in time can be modeled by constructing the states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(t)\rangle = \sum_nc_n(t)|n\rangle } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_n(t) = e^{-\frac{i}{\hbar}E_n t}c_n(0) } . In principle this describes any closed system, and there would never be a reason for time-dependent problems if it were practical to consider all systems as closed. However, there are many examples in nature of systems that are easier described as not being closed. For example, while the stationary approach can be used to describe the interaction of electromagnetic field with atoms (i.e. photon with Hydrogen atom), it is more practical to describe it as an open system with an explicitly time dependent term (due to EM radiation). Therefore we explore Time Dependent Perturbation Theory.
One of the main tasks of this theory is the calculation of transition probabilities from one state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi_n \rangle}
to another state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi_m \rangle}
that occurs under the influence of a time dependent potential. Generally, the transition of a system from one state to another state only makes sense if the potential acts on within a finite time period from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!t = 0}
to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!t = T}
. Except for this time period, the total energy is a constant of motion which can be measured.
We start with the Time Dependent Schrodinger Equation,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial}{\partial t}|\psi_t^0 \rangle = H_0 |\psi_t^0\rangle, \qquad t<t_0. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (2.1.1)}
where a is the Bohr radius. Then, to answer any questions about the behavior of the system at a later time we must find its state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle | \psi_{t} \rangle } , assuming that the perturbation acts after time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!t_0} , we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial}{\partial t}|\psi_t \rangle = (H_0 + V_t)|\psi_t\rangle, \qquad t>t_0 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\;\;\; (2.1.2)}
The problem therefore consists of finding the solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi_t\rangle}
with boundary condition Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi_t\rangle = |\psi_t^0\rangle}
for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t \leq t_0}
. However, such a problem is usually impossible to solve completely in closed form.
Therefore, we limit ourselves to the problems in which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!V_t}
is small. In that case we can treat Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!V_t}
as a perturbation and seek it's effect on the wavefunction in powers of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!V_t}
.
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!V_t} is small, the time dependence of the solution will largely come from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!H_0} . So we use
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi_t\rangle = e^{-i H_0 t/\hbar}|\psi(t)\rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\; (2.1.3)} ,
which we substitute into the Schrodinger Equation to get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial}{\partial t}|\psi(t)\rangle=V(t)|\psi(t)\rangle \quad \text{where}\quad V(t) = e^{i H_0 t/\hbar}V_te^{-i H_0 t/\hbar}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (2.1.4)} .
In this equation and the operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(t)} are in the interaction representation. Now, we integrate equation #(2.1.4) to get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{t_o}^{t}dt \frac{\partial}{\partial t}|\psi(t)\rangle = \psi(t) - \psi(t_0) = \frac{1}{i\hbar}\int_{t_0}^{t}dt' V(t')|\psi(t')\rangle}
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(t)\rangle = |\psi(t_0)\rangle + \frac{1}{i\hbar}\int_{t_0}^{t}dt' V(t')|\psi(t')\rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \;\;\ (2.1.5)}
Equation #(2.1.5) can be iterated by inserting this equation itself as the integrand in the r.h.s. We can then write equation #(2.1.5) as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(t)\rangle = |\psi(t_0)\rangle + \frac{1}{i\hbar}\int_{t_0}^{t}dt' V(t')\left(|\psi(t_0)\rangle + \frac{1}{i\hbar}\int_{t_0}^{t'}dt'' V(t'')|\psi(t'')\rangle\right), \qquad t''<t'\qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\;\ (2.1.6)}
which can be written compactly as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(t)\rangle = T e^{-\frac{i}{\hbar}\int_{t_0}^{t}V(t')dt'} |\psi(t_0) \rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\;\;\ (2.1.7)}
This is the general solution. T is called the time ordering operator, which ensures that the series is expanded in the correct order. For now, we consider only the correction to the first order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!V(t)} .
First Order Transitions
If we limit ourselves to the first order, we use
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(t)\rangle = |\psi(t_0)\rangle + \frac{1}{i\hbar}\int_{t_0}^{t}dt'V(t')|\psi(t_0)\rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\;\;\ (2.1.8)}
We want to see the system undergoes a transition to another state, say Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle}
. So we project the wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(t)\rangle}
to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle}
. From now on, let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(t_0)\rangle = |0\rangle}
for brevity. In other words, what is the probability of a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0\rangle }
making a transition into a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n \rangle }
at a given time t?
Projecting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(t)\rangle } into state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle} and letting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n|0\rangle =0 } if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \neq 0 } , we get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}\langle n|\psi(t)\rangle & = \langle n|0\rangle + \frac{1}{i\hbar}\int_{t_0}^{t}dt'\langle n|V(t')|0\rangle\\ & = \frac{1}{i\hbar}\int_{t_0}^{t}dt'\langle n|e^{\frac{i}{\hbar}H_0 t}V_{t'}e^{-\frac{i}{\hbar}H_0 t}|0\rangle\\ & = \frac{1}{i\hbar}\int_{t_0}^{t}dt'e^{\frac{i}{\hbar}(\epsilon_n - \epsilon_0)t'}\langle n|V_{t'}|0\rangle \end{align}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\;\,\ (2.1.9)}
Expression #(2.1.9) is the probability amplitude of transition. Therefore, we square the final expression to get the probability of having the system in state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle}
at time t.
Squaring, we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{0 \rightarrow n}(t) = |\langle n|\psi(t)\rangle|^2 = \left|\frac{1}{i\hbar}\int_{t_0}^{t}dt' e^{\frac{i}{\hbar}(\epsilon_n - \epsilon_0)t'}\langle n|V_{t'}|0\rangle\right|^2 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\, (2.1.10)}
For example, let us consider a potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!V_t} which is turned on sharply at time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!t_0} , but independent of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t } thereafter. Furthermore, we let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!t_0 = 0} for convenience. Therefore :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_t = \begin{cases} 0 &\mbox{if} \qquad t<0\\ V &\mbox{if} \qquad t>0 \end{cases} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} P_{0 \rightarrow n}(t) & = \left|\frac{1}{i\hbar}\int_{0}^{t}dt' e^{\frac{i}{\hbar}(\epsilon_n - \epsilon_0)t'}\langle n|V|0\rangle\right|^2\\ & = \left|\frac{1}{i\hbar}\frac{e^{\frac{i}{\hbar}(\epsilon_n - \epsilon_0)t}-1}{\frac{i}{\hbar}(\epsilon_n - \epsilon_0)}\langle n|V|0\rangle\right|^2\\ & = \frac{4 \sin^2\left(\frac{\epsilon_n - \epsilon_0}{2\hbar}t\right)}{\left(\epsilon_n - \epsilon_0\right)^2}|\langle n|V|0 \rangle|^2 \end{align}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\;\; (2.1.11) }
The plot of the probability vs. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! \epsilon_n} is given in the following plot:
,where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\epsilon\Delta t \geq 2\pi\hbar} . So we conclude that as the time grows, the probability has a very narrow peak and approximate energy conservation is required for a transition with appreciable probability. However, this "uncertainty relation" is not the same as the fundamental Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x - p } uncertainty relation because while Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p } are both observable variables, time in non-relativistic quantum mechanics is just a parameter, not an observable.
Now, we imagine shining a light of a certain frequency on a hydrogen atom. We probably ended up getting the atom at a certain bound state. However, it might be ionized as well. The problem with ionization is the fact that the final state is a continuum, so we cannot just simply pick up a state to end with i.e. a plane wave with a specific Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k } .
Furthermore, if the wave function is normalized, the plane waves states will contain a factor of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/\sqrt{V}} which goes to zero if is very large. But, we know that ionization exists, so there must be something missing. Instead of measuring the probability to a transition to a pointlike wavenumber, , we want to measure the amplitude of transition to a group of states around a particular , i.e., we want to measure the transition amplitude from to .
Let's suppose that the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle} is one of the continuum state, then what we could ask is the probability that the system makes transition to a small group of states about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle} , not to a specific value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle} . For example, for a free particle, what we can find is the transition probability from initial state to a small group of states, viz. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec k\rangle} , or in other words, the transition probability to an element of phase space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! d^3k / (2\pi)^3}
The next step is a mathematical trick. We use
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta(x) = \lim_{\eta \to 0}\frac{1}{\pi x}\sin\left(\frac{x}{\eta}\right)}
Applying this to our result from above, we see that as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t \rightarrow \infty } ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi \sin(\frac{\epsilon_n - \epsilon_0}{2\hbar}t)}{\pi \hbar \frac{\epsilon_n - \epsilon_0}{2\hbar}} = \frac{\pi}{\hbar}\delta\left(\frac{\epsilon_n - \epsilon_0}{2\hbar}\right) = 2 \pi \delta\left( \epsilon_n - \epsilon_0 \right) \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\;\;\;\;\; (2.1.12)}
If this result used in the equation #2.1.11, it gives
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {P_{0 \rightarrow n}(t)}\quad\underset{t \rightarrow \infty}{\longrightarrow}\quad \frac{t}{\hbar}2\pi \delta(\epsilon_n - \epsilon_0)|\langle n|V|0\rangle|^2 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\;(2.1.13) }
or as a rate of transition, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{0\rightarrow n}} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{0 \rightarrow n} = \frac{d}{dt}P_{0 \rightarrow n}(t)\quad\underset{t \rightarrow \infty}{\longrightarrow}\quad\frac{2\pi}{\hbar} \delta(\epsilon_n - \epsilon_0)|\langle n|V|0\rangle|^2 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (2.1.14) }
which is called The Fermi Golden Rule. Using this formula, we should keep in mind to sum over the entire continuum of final states.
To make things clear, let's try to calculate the transition probability for a system from a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{k}\rangle} to a final state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{k'}\rangle} due to a potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! V(r)} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \vec{k}'|V|\vec{k}\rangle = \int d^3 r \frac{e^{-i\vec{k}'\cdot\vec{r}}}{\sqrt{L^3}}V(r)\frac{e^{i\vec{k}\cdot\vec{r}}}{\sqrt{L^3}} = \frac{V_{k'k}}{L^3} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\;\ (2.1.15) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{\vec{k} \rightarrow \vec{k}'} = \frac{2\pi}{\hbar} \delta(\epsilon_k - \epsilon_{k'})\frac{|V_{k'\rightarrow k}|^2}{L^6}}
What we want is the rate of transition, or actually scattering in this case, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!d\Gamma} into a small solid angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!d\Omega} . So we must sum over the momentum states in this solid angle:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\vec{k}'\in d\Omega}\Gamma_{\vec{k}\rightarrow \vec{k}'} }
The sum over states for continuum can be calculated using an integral,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\vec{k}'\in d\Omega} \quad \longrightarrow \quad d\Omega\int d\epsilon_{\vec{k}'}\frac{L^3 m k'}{(2\pi)^3 \hbar^2}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\;\;\ (2.1.16)}
Therefore,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\Gamma_{\vec{k}\rightarrow{\vec{k}'\in d\Omega}} = \frac{d\Omega}{L^3}\frac{mk}{4\pi^2\hbar^3}|V_{k'k}|^2 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\;\;\;\ (2.1.17)}
The flux of particles per incident particle of momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \vec{k}} in a volume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!L^3} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar k / m L^3} , so
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\Gamma}{d\Omega \left(\frac{\hbar k}{m L^3}\right)} = \frac{m^2}{4\pi^2\hbar^4}\left|V_{k'k}\right|^2 = \frac{d\sigma}{d\Omega}} , in the Born Approximation.
This result makes sense since our potential does not depend on time, so what happened here is that we sent a particle with wave vector through a potential and later detect a particle coming out from that potential with wave vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{k'}} . So, it is a scattering problem solved using a different method.
This is another simple example of transition probability calculation in time dependent perturbation theory with different potential.
Here another example example
An example of the of the first excited state of the hydrogen atom.
Harmonic Perturbation Theory
Harmonic perturbation is one of the main interests in perturbation theory. We know that in experiment, we usually perturb the system using a certain signal to extract information about it, for example the difference between the energy levels. We could send a photon with a certain frequency to a Hydrogen atom to excite the electron and let it decay to observe the difference between two energy levels by measuring the frequency of the photon emitted from it. The photon acts as an electromagnetic signal, and it is harmonic (if we consider it as an electromagnetic wave).
In general, we write down the harmonic perturbation as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!V_t = V cos(\omega t) e^{\eta t}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(2.2.1)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!e^{\eta t}} specifies the rate at which the perturbation is turned on. Since we assume the perturbation is turned on very slowly Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} is a very small positive number which at the end of the calculation, when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0 = -\infty } , is set to be zero.
We start from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!t_0 = - \infty} . Since there's no perturbation at that time. We want to find the probability that there will be a transition from the initial state to some other state, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle | n \rangle} . The transition amplitude is,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!\langle n|\psi_t\rangle = \langle n|e^{\frac{-i}{\hbar}H_0 t}|\psi(t)\rangle = e^{\frac{-i}{\hbar}\epsilon_n t}\langle n|\psi(t)\rangle\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad(2.2.2)}
To the first order of V we write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle n|\psi(t)\rangle & = \frac{1}{i\hbar}\int_{-\infty}^{t}dt' \langle n|V(t')|0\rangle\\ & = \frac{1}{i\hbar}\int_{-\infty}^{t}dt' \langle n|e^{\frac{i}{\hbar}H_0 t'}V_t e^{\frac{-i}{\hbar}H_0 t'}|0\rangle\\ & = \frac{1}{i\hbar}\int_{-\infty}^{t}e^{\frac{i}{\hbar}(\epsilon_n - \epsilon_0)t'}e^{\eta t'}cos(\omega t')\langle n|V|0\rangle\\ & = \frac{\langle n|V|0\rangle}{2i\hbar}\sum_{s=\pm}\int_{-\infty}^{t}dt' e^{\frac{i}{\hbar}(\epsilon_n - \epsilon_0)t'}e^{\eta t'}e^{is\omega t'}\\ & = \frac{\langle n|V|0\rangle}{2i\hbar}\sum_{s=\pm}\frac{e^{\frac{i}{\hbar}(\epsilon_n - \epsilon_0)t}e^{\eta t}e^{is\omega t}}{i(\frac{\epsilon_n - \epsilon_0}{\hbar}+s\omega-i\eta)}\\ & = \frac{\langle n|V|0\rangle}{2} e^{\eta t}\sum_{s = \pm}\frac{e^{\frac{i}{\hbar}(\epsilon_n - \epsilon_0 - s\hbar \omega)t}}{\epsilon_0 - \epsilon_n - s\hbar \omega + i\eta \hbar}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad (2.2.3) \end{align} }
Now we calculate the probability as usual:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |\langle n|\psi_t\rangle|^2 & = \frac{1}{4} |\langle n|V|0\rangle|^2 e^{2\eta t}\sum_{ss'}\frac{e^{{-i}{\hbar}(s-s')\hbar \omega t}}{(\epsilon_0 - \epsilon_n - s\hbar \omega - i\eta \hbar)(\epsilon_0 - \epsilon_n - s\hbar \omega + i\eta \hbar)}\\ \underset{0 \rightarrow n}{P(t)} & = \frac{1}{4}|\langle n|V|0\rangle|^2 e^{2\eta t}\left[\frac{1}{(\epsilon_0 - \epsilon_ n -\hbar\omega)^2 + \eta^2 \hbar^2}+\frac{1}{(\epsilon_0 - \epsilon_n + \hbar \omega)^2+ \eta^2 \hbar^2}\right] \end{align} }
Where all oscillatory terms have been averaged to zero. The transition rate is given by :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \underset{0 \rightarrow n}{\Gamma(t)}=\frac{d{P(t)_{0 \rightarrow n}}}{d t} = \frac{1}{4}|\langle n|V|0\rangle|^2 e^{2\eta t}\left[\frac{2\eta}{(\epsilon_0 - \epsilon_n - \hbar \omega)^2+ \eta^2 \hbar^2}+\frac{2\eta}{(\epsilon_0 - \epsilon_n + \hbar \omega)^2+ \eta^2 \hbar^2}\right] }
Now, if the response is immediate or if the potential is turned on suddenly, we take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta = 0} . Therefore:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \underset{0 \rightarrow n}{\Gamma(t)} = \frac{1}{4}|\langle n|V|0\rangle|^2 \frac{2\pi}{\hbar}\left[\delta(\epsilon_n - \epsilon_0 + \hbar \omega)+\delta(\epsilon_n - \epsilon_0 - \hbar \omega)\right] }
Which is the Fermi Golden Rule. This result shows that there will be a non-zero transition probability for cases where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_n - \epsilon_0 = \mp \hbar \omega}
- Roughly speaking, there will be significant transitions only when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega}
is a "resonant frequency" for a particular transition. The Fermi Golden Rule also shows that it doesn't matter how the potential is turned on -- fast or slow -- the transition rate is not really affected.
Second Order Transitions
Sometimes the first order matrix element Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle f|V|i \rangle } is identically zero (parity, Wigner Eckart, etc.) but other matrix elements are nonzero—and the transition can be accomplished by an indirect route.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^{(2)}_{n}(t)=\left(\frac{1}{i \hbar}\right)^2 \sum_{n}\int_{0}^{t} \int_{0}^{t'} dt' dt'' e^{-i \omega_{f}\left(t-t'\right)}\langle f|V_{S}(t')|n\rangle e^{-i \omega_{n}\left(t'-t''\right)} \langle n|V_{S}(t'')|i\rangle e^{-i \omega_{i} t''} }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^{(2)}_{n}(t) } is the probability amplitude for the second-order process,
Taking the gradually switched-on harmonic perturbation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{S}(t)=e^{\epsilon t} V e^{-i \omega t}} , and the initial time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\infty } , as above
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^{(2)}_{n}(t)=\left(\frac{1}{i \hbar}\right)^2 \sum_{n}\langle f|V|n\rangle \langle n|V|i\rangle e^{-i \omega_{f} t} \int_{-\infty}^{t} dt' \int_{-\infty}^{t'} dt'' e^{i \left(\omega_{f} -\omega_{n} -\omega-i \epsilon\right)t'} e^{i \left(\omega_{n} -\omega_{i} -\omega-i \epsilon\right)t''}}
The integrals are straightforward, and yield
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^{(2)}_{n}(t)=\left(\frac{1}{i \hbar}\right)^2 e^{-i \left(\omega_{i} -\omega_{f}\right)t} \frac{e^{2 \epsilon t}}{\omega_{f} -\omega_{i} -2 \omega-2 i \epsilon} \sum_{n} \frac{\langle f|V|n\rangle \langle n|V|i\rangle}{\omega_{n} -\omega_{i} -\omega-i \epsilon}}
Exactly as in the section above on the first-order Golden Rule, we can find the transition rate:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d}{dt}\left|{c^{(2)}_{n}(t)}\right|^2 = \frac{2 \pi}{\hbar^4} \left|{\sum_{n}\frac{\langle f|V|n\rangle \langle n|V|i\rangle}{\omega_{n} -\omega_{i} -\omega -i \epsilon}}\right|^2 \delta \left(\omega_{f} -\omega_{i} -2 \omega \right)}
The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar^4 }
in the denominator goes to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar }
on replacing the frequencies
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega }
with energies E, both in the denominator and the delta function, remember that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E= \hbar \omega }
This is a transition in which the system gains energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \hbar \omega }
from the beam, in other words two photons are absorbed, the first taking the system to the intermediate energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega }
, which is short-lived and therefore not well defined in energy—there is no energy conservation requirement into this state, only between initial and final states.
Of course, if an atom in an arbitrary state is exposed to monochromatic light, other second order processes in which two photons are emitted, or one is absorbed and one emitted (in either order) are also possible.
Example of Two Level System : Ammonia Maser
This is a very complicate quantum system and there is no way to solve it in a formal form, however we can take some assumptions to solve the problem. In this model, we assume that the Nitrogen atom, being heavier than Hydrogen, is motionless. The Hydrogen atoms form a rigid equilateral triangle whose axis is always passes through the Nitrogen Atom.
Since there are two significant and different states (the position of the Hydrogen triangle), we write down the wave function as a superposition of both states. Of course it is a function of time.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi_t\rangle = C_1(t)|1\rangle + C_2(t)|2\rangle}
Then we operate on this state the time dependent Schrodinger equation to find the eigenvalues:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \begin{pmatrix} \dot{C}_1(t)\\ \dot{C}_2(t) \end{pmatrix} = \begin{pmatrix} E_0 & A\\ A & E_0 \end{pmatrix} \begin{pmatrix} C_1(t)\\ C_2(t) \end{pmatrix} }
In the presence of electric field, the additional energy enters only on the diagonal part of the Hamiltonian matrix
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \begin{pmatrix} \dot{C}_1(t)\\ \dot{C}_2(t) \end{pmatrix} = \begin{pmatrix} E_0 + \mu \varepsilon(t) & A\\ A & E_0 - \mu \varepsilon(t) \end{pmatrix} \begin{pmatrix} C_1(t)\\ C_2(t) \end{pmatrix} }
Typically, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 A \sim 10^{-4} \;\mbox{eV}} which gives the frequency of the movement of the Hydrogen triangle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu \sim 2.4 \times 10^9 \;\mbox{Hz}} and the wavelength Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda \approx 1.25 \;\mbox{cm}} (microwave region).
Solving for the Schrodinger equation we have above, we find the energy of the two states
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_\pm = E_0 \pm \sqrt{(\mu \varepsilon)^2 + A^2}}
The followings are the graphs of the eigenenergy as a function of the applied electric field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon }
Because of these two different states, ammonia molecule is separable in the electric field. This can be used to select molecule with certain value of energy.
It should be clear that if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! \varepsilon(t) = 0} , our eigenstates are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \underbrace{\frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ \pm 1 \end{pmatrix}}_{basis \;for \;expansion}= \; \begin{pmatrix} C_1(0) \\ C_2(0) \end{pmatrix} } with energies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! E_0 \pm A}
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix}C_1(t)\\C_2(t)\end{pmatrix}=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\1\end{pmatrix} \gamma_1(t)+\frac{2}{\sqrt{2}}\begin{pmatrix}1\\-1\end{pmatrix} \gamma_2(t)} , then we find
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\hbar \dot{\gamma_1} & = & (E_0 +A)\gamma_1 + \mu \varepsilon(t)\gamma_2\\ i\hbar \dot{\gamma_2} & = & (E_0 -A)\gamma_2 + \mu \varepsilon(t)\gamma_1 \end{align} }
Now, let
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \gamma_1(t) & = e^{-\frac{i}{\hbar}(E_0 + A)t}\alpha(t)\\ \gamma_2(t) & = e^{-\frac{i}{\hbar}(E_0 - A)t}\beta(t) \end{align} }
Also, we define the electric field as a function of time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon(t) = 2\varepsilon_0 \cos\omega t = \varepsilon_0(e^{i\omega t}+e^{-i \omega t})} so the above expression can be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\hbar \dot{\alpha}(t) & = \mu \varepsilon_0 (e^{i(\omega + \frac{2A}{\hbar})t}+e^{-i(\omega - \frac{2A}{\hbar})t})\beta(t)\\ i\hbar \dot{\beta}(t) & = \mu \varepsilon_0 (e^{i(\omega - \frac{2A}{\hbar})t}+e^{-i(\omega + \frac{2A}{\hbar})t})\alpha(t) \end{align} }
Now, we observe that as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! \omega \rightarrow \frac{2A}{\hbar} = \omega_0} the first term in the right hand side of the first equation will oscillate very rapidly compared to the second term of the same equation. The average of this rapid oscillating term will be zero. So we don't need to consider these oscillating terms in the next calculation. Therefore we get a result
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\hbar\dot{\alpha}(t) & = \mu \varepsilon_0 e^{-i(\omega - \omega_0)t}\beta(t)\\ i\hbar\dot{\beta}(t) & = \mu \varepsilon_0 e^{i(\omega - \omega_0)t}\alpha(t) \end{align} }
At resonance, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! \omega = \omega_0} , these equations are simplified to
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\hbar\dot{\alpha}(t) & = \mu \varepsilon_0 \beta(t)\\ i\hbar\dot{\beta}(t) & = \mu \varepsilon_0 \alpha(t) \end{align} }
We can then differentiate the first equation with respect to time and substitute the second equation into it to get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \ddot{\alpha} =\mu \varepsilon_0 \left(\frac{\mu \varepsilon_0}{i\hbar}\alpha\right) \Rightarrow \ddot{\alpha}=-\left(\frac{\mu\varepsilon_0}{\hbar} \right)^2 \alpha}
With solution (also for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta } with substitution)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \alpha(t) & = a \cos\left(\frac{\mu \varepsilon_0}{\hbar}t\right) + b \sin\left(\frac{\mu \varepsilon_0}{\hbar}t\right)\\ \beta(t) & = ib \cos\left(\frac{\mu \varepsilon_0}{\hbar}t\right) - ia \sin\left(\frac{\mu \varepsilon_0}{\hbar}t\right) \end{align} }
Let's assume that at time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! t = 0} , the molecule is in state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1\rangle } (experimentally, we can prepare the molecule to be in this state) so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = 1 \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b = 0\!} . This assumption gives
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix} \alpha(t) \!\!\! &=& \!\!\! \cos\left(\frac{\mu \varepsilon_0}{\hbar}t\right) \\ \beta(t) \!\!\! &=& \!\!\! -i \sin\left(\frac{\mu \varepsilon_0}{\hbar}t\right) \end{matrix} \; \Rightarrow \; \begin{matrix} \gamma_1(t) \!\!\! &=& \!\!\! e^{-i\frac{i}{\hbar}(E_0 + A)t} \cos\left(\frac{\mu \varepsilon_0}{\hbar}t\right) \\ \gamma_2(t) \!\!\! &=& \!\!\! -ie^{-i\frac{i}{\hbar}(E_0 - A)t} \sin\left(\frac{\mu \varepsilon_0}{\hbar}t\right) \end{matrix} }
Therefore the each probability that the molecule remains in the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |+\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |-\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ -1 \end{pmatrix} } is :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} P_+(t) & = |\gamma_1(t)|^2 = \cos^2\left(\frac{\mu \varepsilon_0}{\hbar}t\right)\\ P_-(t) & = |\gamma_2(t)|^2 = \sin^2\left(\frac{\mu \varepsilon_0}{\hbar}t\right) \end{align} }
Note that the probability depends on time. The molecules enter in upper energy state. If the length of the cavity is chosen appropriately, the molecules will come out surely in lower energy state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{-}=1} . If that is the case, the molecules lost some energy and, in reverse, the cavity gains the same amount of energy. The cavity is therefore excited and then produces stimulated emission. That is the mechanism of a MASER which stands for Microwave Amplification by Stimulated Emission of Radiation.
Interaction of radiation and matter
The conventional treatment of quantum mechanics uses time-independent wavefunctions with the Schrödinger equation to determine the energy levels (eigenvalues) of a system. To understand the interaction of radiation (electromagnetic radiation) and matter, we need to consider the time-dependent Schrödinger equation.
Quantization of electromagnetic radiation
Classical view
Let's use transverse gauge (sometimes called Coulomb gauge) which give us:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi (\mathbf{r},t)=0 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \cdot \mathbf{A}=0}
In this gauge the electromagnetic fields are given by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{E}(\mathbf{r},t)=-\frac{1}{c}\frac{\partial \mathbf{A} }{\partial t}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{B}(\mathbf{r},t)=\nabla \times \mathbf{A}}
The energy in this radiation is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon = \frac{1}{8\pi} \int d^{3} r (\mathbf{E}^{2}+\mathbf{B}^{2})}
The rate and direction of energy transfer are given by Poynting vector
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{P} = \frac{c}{4\pi} \mathbf{E} \times \mathbf{B} }
The radiation generated by classical current is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Box \mathbf{A} = -\frac{4\pi}{c} \mathbf{j}}
Where is the d'Alembert operator. Solutions in the region where are given by
where and , as we are considering EM waves in vacuum. The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\lambda}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\lambda^*}} are the two general polarization vectors, perpendicular to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}} . Note that, in general,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\mathbf{k}}\times\hat{\boldsymbol{\lambda}} = \hat{\boldsymbol{\lambda^*}}; \hat{\boldsymbol{\lambda}}\times\hat{\boldsymbol{\lambda^*}} = \hat{\mathbf{k}}; \hat{\boldsymbol{\lambda^*}}\times\hat{\mathbf{k}} = \hat{\boldsymbol{\lambda}} }
Here the plane waves are normalized with respect to some volume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} . This is just for convenience and the physics won't change. Note that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\lambda}\cdot\boldsymbol{\lambda}^{*}=1} , as the polarization vectors are unit vectors. Notice that in this writing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A}} is a real vector.
Let's compute Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} . For this
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{E}(\mathbf{r},t) & =-\frac{1}{c}\frac{\partial \mathbf{A} }{\partial t} \\ & =-\frac{1}{c\sqrt{V}}\frac{\partial}{\partial t}\left[\alpha \boldsymbol{\lambda}e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}+\alpha^{*} \boldsymbol{\lambda}^{*} e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}\right] \\ & =-\frac{i\omega}{c\sqrt{V}}\left[-\alpha \boldsymbol{\lambda} e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}+\alpha^{*} \boldsymbol{\lambda}^{*} e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}\right] \\ \mathbf{E}^{2}(\mathbf{r},t) & = \frac{\omega^{2}}{c^{2}V}\left[\alpha\alpha^{*} \boldsymbol{\lambda}\cdot\boldsymbol{\lambda}^{*} - \alpha\alpha \boldsymbol{\lambda}\cdot\boldsymbol{\lambda} e^{2i(\mathbf{k}\cdot\mathbf{r}-\omega t)}-\alpha^{*}\alpha^{*}\boldsymbol{\lambda}^{*}\cdot\boldsymbol{\lambda}^{*} e^{-2i(\mathbf{k}\cdot\mathbf{r}-\omega t)} + \alpha^{*}\alpha\boldsymbol{\lambda}\cdot\boldsymbol{\lambda}^{*}\right] \\ \end{align} }
Taking the average, the oscillating terms will disappear. Then we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{E}^{2}(\mathbf{r}) & = \frac{\omega^{2}}{c^{2}V}\left[\alpha\alpha^{*}+\alpha^{*}\alpha\right] \\ &=2\frac{\omega^{2}}{c^{2}V}|\alpha|^2 \\ \end{align} }
It is well known that for plane waves Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{B}=\mathbf{n}\times \mathbf{E} } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{n}} is the direction of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}} . This clearly shows that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{B}^{2}=\mathbf{E}^{2}} . However, let's see this explicitly:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{B}(\mathbf{r},t) & =\nabla \times\mathbf{A}\\ & =\nabla \times \left[\alpha \boldsymbol{\lambda}\frac{e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}+\alpha^{*} \boldsymbol{\lambda}^{*} \frac{e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}\right] \\ \end{align} }
Each component is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{B}_{i}(\mathbf{r},t)& =\frac{1}{{\sqrt{V}}}\left[\alpha \varepsilon _{ijk}\partial_{j} \left(\boldsymbol{\lambda}_{k}e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}\right)+\alpha^{*} \varepsilon _{ijk}\partial_{j} \left(\boldsymbol{\lambda}^{*}_{k}e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}\right)\right] \\ & =\frac{i}{{\sqrt{V}}}\left[\alpha \varepsilon _{ijk}\mathbf{k}_{j} \boldsymbol{\lambda}_{k}e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}-\alpha^{*} \varepsilon _{ijk}\mathbf{k}_{j} \boldsymbol{\lambda}^{*}_{k}e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}\right] \\ \end{align} }
Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{B}(\mathbf{r},t) & =\frac{i}{{\sqrt{V}}}\left[\alpha \mathbf{k}\times\boldsymbol{\lambda}e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}-\alpha^{*} \mathbf{k}\times\boldsymbol{\lambda}^{*} e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}\right] \\ \mathbf{B}^{2}(\mathbf{r},t) & =\frac{1}{{V}}\left[\alpha \mathbf{k}\times\boldsymbol{\lambda}e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}-\alpha^{*} \mathbf{k}\times\boldsymbol{\lambda}^{*} e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}\right] \left[\alpha \mathbf{k}\times\boldsymbol{\lambda}e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}-\alpha^{*} \mathbf{k}\times\boldsymbol{\lambda}^{*} e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}\right]^{*} \\ & =\frac{1}{{V}}\left[\alpha\alpha^{*} \left(\mathbf{k}\times\boldsymbol{\lambda}\right)\cdot\left(\mathbf{k}\times\boldsymbol{\lambda}^{*}\right) -\alpha \alpha\left(\mathbf{k}\times\boldsymbol{\lambda}\right)\cdot\left(\mathbf{k}\times\boldsymbol{\lambda}\right) e^{2i(\mathbf{k}\cdot\mathbf{r}-\omega t)}-\alpha^{*} \alpha^{*} \left(\mathbf{k}\times\boldsymbol{\lambda}^{*}\right)\cdot\left(\mathbf{k}\times\boldsymbol{\lambda}^{*}\right) e^{-2i(\mathbf{k}\cdot\mathbf{r}-\omega t)} + \alpha^{*} \alpha \left(\mathbf{k}\times\boldsymbol{\lambda}^{*}\right)\cdot \left(\mathbf{k}\times\boldsymbol{\lambda}\right) \right] \\ \end{align} }
Again, taking the average the oscillating terms vanish. Then we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{B}^{2}(\mathbf{r}) & =\frac{1}{{V}}\left[\alpha \alpha^{*}+\alpha^{*} \alpha\right](\mathbf{k}\times\boldsymbol{\lambda})\cdot(\mathbf{k}\times\boldsymbol{\lambda}^{*}) \\ & =\frac{1}{{V}}\left[\alpha \alpha^{*}+\alpha^{*} \alpha\right][\mathbf{k}^{2}(\boldsymbol{\lambda}\cdot\boldsymbol{\lambda^{*}})-(\mathbf{k}\cdot\boldsymbol{\lambda^{*}})(\mathbf{k}\cdot\boldsymbol{\lambda})] \\ & =\frac{2}{{V}}|\alpha|^{2}\mathbf{k}^{2}\\ &=2\frac{\omega^{2}}{c^{2}V}|\alpha|^2 \\ &= \mathbf{E}^{2}(\mathbf{r},t)\\ \end{align} }
Finally the energy of this radiation is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \varepsilon &= \frac{1}{8\pi} \int d^{3}r (\mathbf{E}^{2}+\mathbf{B}^{2}) \\ &=\frac{1}{4\pi} \int d^{3}r\; \mathbf{E}^{2}\\ &=\frac{1}{4\pi} \int d^{3}r \left(2\frac{\omega^{2}}{c^{2}V}|\alpha|^2\right)\\ &=\frac{\omega^{2}}{2\pi c^{2}}|\alpha|^2\\ \end{align}}
So far, we have treated the potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A}(\mathbf{r},t)} as a combination of two waves with the same frequency. Now let's extend the discussion to any form of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A}(\mathbf{r},t)} . To do this, we can sum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A}(\mathbf{r},t)} over all values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\lambda}} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{A}(\mathbf{r},t)=\sum_{\mathbf{k}\boldsymbol{\lambda}} \left[A_{\mathbf{k}\boldsymbol{\lambda}} \boldsymbol{\lambda}\frac{e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}+A_{\mathbf{k}\boldsymbol{\lambda}}^{*} \boldsymbol{\lambda}^{*} \frac{e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}} \right]\\ \end{align}}
To calculate the energy with useing the fact that any exponential time-dependent term is on average zero. Therefore, in the previous sum all cross terms with different Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}} vanishes. Then, it is clear that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{E}^{2}(\mathbf{r}) & = \sum_{\mathbf{k}\boldsymbol{\lambda}}\frac{\omega^{2}}{c^{2}V}\left[A_{\mathbf{k}\boldsymbol{\lambda}}A_{\mathbf{k}\boldsymbol{\lambda}}^{*}+A_{\mathbf{k}\boldsymbol{\lambda}}^{*}A_{\mathbf{k}\boldsymbol{\lambda}}\right] \\ \mathbf{B}^{2}(\mathbf{r}) & = \sum_{\mathbf{k}\boldsymbol{\lambda}}\frac{\mathbf{k}^2}{V}\left[A_{\mathbf{k}\boldsymbol{\lambda}}A_{\mathbf{k}\boldsymbol{\lambda}}^{*}+A_{\mathbf{k}\boldsymbol{\lambda}}^{*}A_{\mathbf{k}\boldsymbol{\lambda}}\right] \\ \end{align} }
Then, the energy is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \varepsilon &= \frac{1}{8\pi} \int d^{3}r (\mathbf{E}^{2}+\mathbf{B}^{2}) \\ &=\frac{1}{4\pi} \int d^{3}r\; \mathbf{E}^{2}\\ &=\frac{1}{4\pi} \int d^{3}r \sum_{\mathbf{k}\boldsymbol{\lambda}}\frac{\omega^{2}}{c^{2}V}\left[A_{\mathbf{k}\boldsymbol{\lambda}}A_{\mathbf{k}\boldsymbol{\lambda}}^{*}+A_{\mathbf{k}\boldsymbol{\lambda}}^{*}A_{\mathbf{k}\boldsymbol{\lambda}}\right] \\ &=\frac{1}{4\pi} \sum_{\mathbf{k}\boldsymbol{\lambda}}\frac{\omega^{2}}{c^{2}}\left[A_{\mathbf{k}\boldsymbol{\lambda}}A_{\mathbf{k}\boldsymbol{\lambda}}^{*}+A_{\mathbf{k}\boldsymbol{\lambda}}^{*}A_{\mathbf{k}\boldsymbol{\lambda}}\right] \\ \end{align}}
Let's define the following quantities:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} Q_{\mathbf{k}\boldsymbol{\lambda}}&=\frac{1}{\sqrt{4\pi}c}(A_{\mathbf{k}\boldsymbol{\lambda}}+A_{\mathbf{k}\boldsymbol{\lambda}}^{*})\\ P_{\mathbf{k}\boldsymbol{\lambda}}&=\frac{-i\omega}{\sqrt{4\pi}c}(A_{\mathbf{k}\boldsymbol{\lambda}}-A_{\mathbf{k}\boldsymbol{\lambda}}^{*})\\ \end{align}}
Notice that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \omega^{2} Q_{\mathbf{k}\boldsymbol{\lambda}}^{2}&=\frac{\omega^{2}}{4\pi c^{2}}(A_{\mathbf{k}\boldsymbol{\lambda}}^{2}+A_{\mathbf{k}\boldsymbol{\lambda}}\cdot A_{\mathbf{k}\boldsymbol{\lambda}}^{*}+A_{\mathbf{k}\boldsymbol{\lambda}}^{*}\cdot A_{\mathbf{k}\boldsymbol{\lambda}}+A_{\mathbf{k}\boldsymbol{\lambda}}^{*2})\\ P_{\mathbf{k}\boldsymbol{\lambda}}^{2}&=\frac{-\omega^{2}}{4\pi c^{2}}(A_{\mathbf{k}\boldsymbol{\lambda}}^{2}-A_{\mathbf{k}\boldsymbol{\lambda}}\cdot A_{\mathbf{k}\boldsymbol{\lambda}}^{*}-A_{\mathbf{k}\boldsymbol{\lambda}}^{*}\cdot A_{\mathbf{k}\boldsymbol{\lambda}}+A_{\mathbf{k}\boldsymbol{\lambda}}^{*2})\\ \end{align}}
Adding
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} P_{\mathbf{k}\boldsymbol{\lambda}}^{2}+\omega^{2} Q_{\mathbf{k}\boldsymbol{\lambda}}^{2}&=\frac{\omega^{2}}{2\pi c^{2}}(A_{\mathbf{k}\boldsymbol{\lambda}}\cdot A_{\mathbf{k}\boldsymbol{\lambda}}^{*}+A_{\mathbf{k}\boldsymbol{\lambda}}^{*}\cdot A_{\mathbf{k}\boldsymbol{\lambda}})\\ \end{align}}
Then the energy (in this case the Hamiltonian) can be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} H=\frac{1}{2}\sum_{\mathbf{k}\boldsymbol{\lambda}} [P_{\mathbf{k}\boldsymbol{\lambda}}^{2}+\omega^{2} Q_{\mathbf{k}\boldsymbol{\lambda}}^{2}] \end{align}}
This has the same form as the familiar Hamiltonian for a harmonic oscillator.
Note that,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{\partial H_{cl}}{\partial Q_{k, \lambda}} &= - \dot{P}_{k, \lambda} \\ \frac{\partial H_{cl}}{\partial P_{k, \lambda}} &= \dot{Q}_{k, \lambda} \end{align}}
The makeshift variables, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{k, \lambda}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q_{k, \lambda}} are canonically conjugate.
We see that the classical radiation field behaves as a collection of harmonic oscillators, indexed by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\lambda}} , whose frequencies depends on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\mathbf{k}|} .
From classical mechanics to quatum mechanics for radiation
As usual we proceed to do the canonical quantization:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} P_{\mathbf{k}\boldsymbol{\lambda}} & \to \mathbf{P}_{\mathbf{k}\boldsymbol{\lambda}}\\ Q_{\mathbf{k}\boldsymbol{\lambda}} & \to \mathbf{Q}_{\mathbf{k}\boldsymbol{\lambda}}\\ \end{align}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} A_{\mathbf{k}\boldsymbol{\lambda}} & \to \sqrt{\frac{2\pi \hbar c^{2}}{\omega_{\mathbf{k}}}}\;\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\; , \; [\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}},\mathbf{a}^{\dagger}_{\mathbf{k'}\boldsymbol{\lambda'}}]=\delta_{\mathbf{kk'}}\delta_{\boldsymbol{\lambda \lambda'}}\\ \end{align}}
Where last are quantum operators. The Hamiltonian can be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{H}_{radiation}&=\sum_{\mathbf{k}\boldsymbol{\lambda}}\hbar \omega_{\mathbf{k}}(\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}} \mathbf{a}_{\mathbf{k} \boldsymbol{\lambda}}+\frac{1}{2}) &=\frac{1}{2}\sum_{\mathbf{k}\boldsymbol{\lambda}}\hbar \omega_{\mathbf{k}}(\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}} \mathbf{a}_{\mathbf{k} \boldsymbol{\lambda}}+\mathbf{a}_{\mathbf{k} \boldsymbol{\lambda}} \mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}})\\ \end{align}}
The classical potential can be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \underbrace{\mathbf{A}(\mathbf{r},t)=\sum_{\mathbf{k}\boldsymbol{\lambda}} \left[A_{\mathbf{k}\boldsymbol{\lambda}} \boldsymbol{\lambda}\frac{e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}+A_{\mathbf{k}\boldsymbol{\lambda}}^{*} \boldsymbol{\lambda}^{*} \frac{e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}\right]}_\textrm{Classical Vector potential}\;\;\;\longrightarrow\;\;\; \underbrace{\mathbf{A}_{int}(\mathbf{r},t)=\sum_{\mathbf{k}\boldsymbol{\lambda}} \sqrt{\frac{2\pi \hbar c^{2}}{\omega_{\mathbf{k}}}}\left[\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}} \boldsymbol{\lambda}\frac{e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}+\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger} \boldsymbol{\lambda}^{*} \frac{e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}\right]}_\textrm{Quantum Operator} }
Notice that the quantum operator is time dependent. Therefore we can identify it as the field operator in interaction representation. (That's the reason to label it with int). Let's find the Schrodinger representation of the field operator:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{A}(\mathbf{r})&=e^{-\frac{i}{\hbar}\mathbf{H}_{rad}t}\mathbf{A}_{int}(\mathbf{r},t)e^{\frac{i}{\hbar}\mathbf{H}_{rad}t}\\ &=e^{-\frac{i}{\hbar}\mathbf{H}_{rad}t}\left[\sum_{\mathbf{k}\boldsymbol{\lambda}} \sqrt{\frac{2\pi \hbar c^{2}}{\omega_{\mathbf{k}}}}\left[\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}} \boldsymbol{\lambda}\frac{e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}+\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger} \boldsymbol{\lambda}^{*} \frac{e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}\right]\right]e^{\frac{i}{\hbar}\mathbf{H}_{rad}t}\\ &=\sum_{\mathbf{k}\boldsymbol{\lambda}} \sqrt{\frac{2\pi \hbar c^{2}}{\omega_{\mathbf{k}}}}\left[\left[e^{-\frac{i}{\hbar}\mathbf{H}_{rad}t} \mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}e^{\frac{i}{\hbar}\mathbf{H}_{rad}t}\right] \boldsymbol{\lambda}\frac{e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}+\left[ e^{-\frac{i}{\hbar}\mathbf{H}_{rad}t}\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger} e^{\frac{i}{\hbar}\mathbf{H}_{rad}t}\right] \boldsymbol{\lambda}^{*} \frac{e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}\right]\\ &=\sum_{\mathbf{k}\boldsymbol{\lambda}} \sqrt{\frac{2\pi \hbar c^{2}}{\omega_{\mathbf{k}}}}\left[\left[\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}e^{i\omega t}\right] \boldsymbol{\lambda}\frac{e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}+\left[ \mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger} e^{-i\omega t}\right] \boldsymbol{\lambda}^{*} \frac{e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}\right]\\ &=\sum_{\mathbf{k}\boldsymbol{\lambda}} \sqrt{\frac{2\pi \hbar c^{2}}{\omega_{\mathbf{k}}}}\left[\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}} \boldsymbol{\lambda}\frac{e^{i\mathbf{k}\cdot\mathbf{r}}}{\sqrt{V}}+\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger} \boldsymbol{\lambda}^{*} \frac{e^{-i\mathbf{k}\cdot\mathbf{r}}}{\sqrt{V}}\right]\\ \end{align}}
COMMENTS
- The meaning of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_{radiation}} is as following: The classical electromagnetic field is quantized. This quantum field exist even if there is not any source. This means that the vacuum is a physical object who can interact with matter. In classical mechanics this doesn't occur because, fields are created by sources.
- Due to this, the vacuum has to be treated as a quantum dynamical object. Therefore we can define to this object a quantum state.
- The perturbation of this quantum field is called photon (it is called the quanta of the electromagnetic field).
ANALYSIS OF THE VACUUM AT GROUND STATE
Let's call Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0\rangle} the ground state of the vacuum. The following can be stated:
- The energy of the ground state is infinite. To see this notice that for ground state we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{H}_{radiation}&=\sum_{\mathbf{k}\boldsymbol{\lambda}} \frac{1}{2} \hbar \omega_{\mathbf{k}}=\infin \end{align}}
- The state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}|0\rangle} represent an exited state of the vacuum with energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega_{\mathbf{k}}(1+1/2)} . This means that the extra energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega_{\mathbf{k}}} is carried by a single photon. Therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}} represent the creation operator of one single photon with energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega_{\mathbf{k}}} . In the same reasoning, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}_{\mathbf{k} \boldsymbol{\lambda}}} represent the annihilation operator of one single photon.
- Consider the following normalized state of the vacuum:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{2}}\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}|0\rangle}
. At the first glance we may think that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}}
creates a single photon with energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\hbar \omega_{\mathbf{k}}}
. However this interpretation is forbidden in our model. Instead, this operator will create two photons each of the carryng the energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega_{\mathbf{k}}}
.
Proof
Suppose that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}} creates a single photon with energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\hbar \omega_{\mathbf{k}}} . We can find an operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}^{\dagger}_{\mathbf{k'} \boldsymbol{\lambda}}} who can create a photon with the same energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\hbar \omega_{\mathbf{k}}} . This means that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{2}}\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}|0\rangle\overset{\underset{\mathrm{?}}{}}{=} \mathbf{a}^{\dagger}_{\mathbf{k'} \boldsymbol{\lambda}}|0\rangle \;\;\;\longrightarrow\;\;\;\frac{1}{\sqrt{2}}\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}} \overset{\underset{\mathrm{?}}{}}{=} \mathbf{a}^{\dagger}_{\mathbf{k'} \boldsymbol{\lambda}}\;\;\;\longrightarrow\;\;\;\frac{1}{\sqrt{2}}\mathbf{a}_{\mathbf{k} \boldsymbol{\lambda}}\mathbf{a}_{\mathbf{k} \boldsymbol{\lambda}} \overset{\underset{\mathrm{?}}{}}{=} \mathbf{a}_{\mathbf{k'} \boldsymbol{\lambda}} }
Let's see if this works. Using commutation relationship we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ \underbrace{\mathbf{a}_{\mathbf{k} \boldsymbol{\lambda}}\mathbf{a}_{\mathbf{k} \boldsymbol{\lambda}}},\mathbf{a}^{\dagger}_{\mathbf{k'} \boldsymbol{\lambda}}\right]=0 }
Replace the highlighted part by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}_{\mathbf{k'} \boldsymbol{\lambda}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[\mathbf{a}_{\mathbf{k'} \boldsymbol{\lambda}},\mathbf{a}^{\dagger}_{\mathbf{k'} \boldsymbol{\lambda}}\right]=0 }
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[\mathbf{a}_{\mathbf{k'} \boldsymbol{\lambda}},\mathbf{a}^{\dagger}_{\mathbf{k'} \boldsymbol{\lambda}}\right]=1} , the initial assumption is wrong, namely:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{2}}\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}|0\rangle \ne \mathbf{a}^{\dagger}_{\mathbf{k'} \boldsymbol{\lambda}}|0\rangle }
This means that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}}\mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}} } cannot create a single photon with energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\hbar \omega_{\mathbf{k}}} . Instead it will create two photons each of them with energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega_{\mathbf{k}\blacksquare}}
ALGEBRA OF VACUUM STATES
A general vacuum state can be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_{\mathbf{k_{1}} \boldsymbol{\lambda_{1}}};n_{\mathbf{k_{2}} \boldsymbol{\lambda_{2}}};...;n_{\mathbf{k_{i}} \boldsymbol{\lambda_{i}}};...\rangle }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{\mathbf{k_{i}} \boldsymbol{\lambda_{i}}}} is the number of photons in the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k_{i}} \boldsymbol{\lambda_{i}}} which exist in the vacuum. Using our knowledge of harmonic oscillator we conclude that this state can be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_{\mathbf{k_{1}} \boldsymbol{\lambda_{1}}};n_{\mathbf{k_{2}} \boldsymbol{\lambda_{2}}};...;n_{\mathbf{k_{i}} \boldsymbol{\lambda_{i}}};...\rangle=\prod_{\mathbf{k_{j}} \boldsymbol{\lambda_{j}}}\frac{( \mathbf{a}^{\dagger}_{\mathbf{k} \boldsymbol{\lambda}})^{n_{\mathbf{k_{j}} \boldsymbol{\lambda_{j}}}}}{\sqrt{n_{\mathbf{k_{j}} \boldsymbol{\lambda_{j}}}!}}|0\rangle }
Also it is clear that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}^{\dagger}_{\mathbf{k_{i}} \boldsymbol{\lambda_{i}}}|n_{\mathbf{k_{1}} \boldsymbol{\lambda_{1}}};n_{\mathbf{k_{2}} \boldsymbol{\lambda_{2}}};...;n_{\mathbf{k_{i}} \boldsymbol{\lambda_{i}}};...\rangle=\sqrt{n_{\mathbf{k_{i}} \boldsymbol{\lambda_{i}}}+1}|n_{\mathbf{k_{1}} \boldsymbol{\lambda_{1}}};n_{\mathbf{k_{2}} \boldsymbol{\lambda_{2}}};...;n_{\mathbf{k_{i}} \boldsymbol{\lambda_{i}}}+1;...\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}_{\mathbf{k_{i}} \boldsymbol{\lambda_{i}}}|n_{\mathbf{k_{1}} \boldsymbol{\lambda_{1}}};n_{\mathbf{k_{2}} \boldsymbol{\lambda_{2}}};...;n_{\mathbf{k_{i}} \boldsymbol{\lambda_{i}}};...\rangle=\sqrt{n_{\mathbf{k_{i}} \boldsymbol{\lambda_{i}}}}|n_{\mathbf{k_{1}} \boldsymbol{\lambda_{1}}};n_{\mathbf{k_{2}} \boldsymbol{\lambda_{2}}};...;n_{\mathbf{k_{i}} \boldsymbol{\lambda_{i}}}-1;...\rangle }
Matter + Radiation
Hamiltonian of Single Particle in Presence of Radiation (Gauge Invariance)
The Hamiltonian of a single charged particle in presence of E&M potentials is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}=\frac{\left[\vec{p}-\frac{e}{c}\vec{A}(\vec{r},t)\right]^{2}}{2m}+e\phi (\vec{r},t) + V(\vec{r},t), }
where the vector potential in the first term and the scalar potential in the second term is external E-M interaction and the third term is related to other potentials.
The time dependent Schrödinger equation is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \frac{\partial\psi (\vec{r},t)}{\partial t}=\left[\frac{\left[\vec{p}-\frac{e}{c}\vec{A}(\vec{r},t)\right]^{2}}{2m}+e\phi (\vec{r},t) + V(\vec{r},t) \right]\psi(\vec{r},t) }
Since a gauge transformation,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A'_{\mu}=A_{\mu}-\partial_{\mu} \chi , }
left invariant the E&M fields, we expect that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi|^{2} \!} which is an observable is also gauge independent. Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi|^{2} \!} is independent of the phase choice, we can relate this phase with the E&M gauge transformation. In other words, the phase transformation with E&M transformation must leave Schrödinger equation invariant. This phase transformation is given by:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi'(\vec{r},t)=e^{i\frac{e}{\hbar c}\chi(\vec{r},t)}\psi(\vec{r},t) }
Let's see this in detail. We want to see if:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\hbar \frac{\partial\psi' (\vec{r},t)}{\partial t} & =\left[\frac{\left[\vec{p}-\frac{e}{c}\vec{A}'(\vec{r},t)\right]^{2}}{2m}+e\phi '(\vec{r},t) + V(\vec{r},t) \right]\psi'(\vec{r},t) \\ & = \left[\frac{\left[\vec{p}-\frac{e}{c}\vec{A}(\vec{r},t)\right]^{2}}{2m}+e\phi (\vec{r},t) + V(\vec{r},t) \right]\psi(\vec{r},t) = i\hbar \frac{\partial\psi(\vec{r},t)}{\partial t} \end{align} }
Let's put the transformations:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \psi'(\vec{r},t)&=e^{i\frac{e}{\hbar c}\chi(\vec{r},t)}\psi(\vec{r},t) \\ \vec{A}'(\vec{r},t)&=\vec{A}(\vec{r},t)+\vec{\nabla} \chi(\vec{r},t) \\ \phi'(\vec{r},t)&=\phi(\vec{r},t)-\frac{1}{c}\frac{\partial\chi(\vec{r},t) }{\partial t} \end{align}}
Replacing
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\hbar \left[\frac{ie}{\hbar c} \frac{\partial \chi}{\partial t} e^{i\frac{e}{\hbar c}\chi}\psi + e^{i\frac{e}{\hbar c}\chi} \frac{\partial \psi}{\partial t} \right] &= \left[\frac{\left[\vec{p}-\frac{e}{c}\vec{A}'\right]^{2}}{2m}+e\phi -\frac{e}{c} \frac{\partial \chi}{\partial t} + V \right]e^{i\frac{e}{\hbar c}\chi}\psi\\ i\hbar e^{i\frac{e}{\hbar c}\chi} \frac{\partial \psi}{\partial t} &= \left[\frac{\left[\vec{p}-\frac{e}{c} \vec{A}'\right]^{2}}{2m}+e\phi + V \right]e^{i\frac{e}{\hbar c}\chi}\psi\\ i\hbar \frac{\partial \psi}{\partial t} &= \left[\frac{1}{2m} e^{-i\frac{e}{\hbar c}\chi}\left[\vec{p}-\frac{e}{c}\vec{A}'\right]^{2}e^{i\frac{e}{\hbar c}\chi} +e\phi + V \right]\psi\\ i\hbar \frac{\partial \psi}{\partial t} &= \left[\frac{1}{2m} e^{-i\frac{e}{\hbar c}\chi}\left[\vec{p}-\frac{e}{c}\vec{A}'\right]e^{i\frac{e}{\hbar c}\chi}e^{-i\frac{e}{\hbar c}\chi}\left[\vec{p}-\frac{e}{c}\vec{A}'\right]e^{i\frac{e}{\hbar c}\chi} +e\phi + V \right]\psi\\ i\hbar \frac{\partial \psi}{\partial t} &= \left[\frac{1}{2m} \left(e^{-i\frac{e}{\hbar c}\chi}\left[\vec{p}-\frac{e}{c}\vec{A}'\right]e^{i\frac{e}{\hbar c}\chi}\right) ^{2} +e\phi + V \right]\psi\\ i\hbar \frac{\partial \psi}{\partial t} &= \left[\frac{1}{2m} \left(e^{-i\frac{e}{\hbar c}\chi}\left[\frac{\hbar}{i}\vec{\nabla}-\frac{e}{c}\vec{A}-\frac{e}{c}\vec{\nabla} \chi\right]e^{i\frac{e}{\hbar c}\chi}\right) ^{2} +e\phi + V \right]\psi\\ i\hbar \frac{\partial \psi}{\partial t} &= \left[\frac{1}{2m} \left(e^{-i\frac{e}{\hbar c}\chi}e^{i\frac{e}{\hbar c}\chi}\left[\frac{\hbar}{i} \frac{ie}{\hbar c}\nabla \chi + \frac{\hbar}{i}\vec{\nabla}-\frac{e}{c}\vec{A}-\frac{e}{c}\vec{\nabla} \chi\right]\right) ^{2} +e\phi + V \right]\psi\\ i\hbar \frac{\partial \psi}{\partial t} &= \left[\frac{1}{2m} \left(\frac{\hbar}{i}\vec{\nabla}-\frac{e}{c}\vec{A} \right) ^{2} +e\phi + V \right]\psi = (no\; prime)_{ \blacksquare}\\ \end{align}}
Finally let's write the Hamiltonian in the following way
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}=\underbrace{\frac{\vec{p}^2}{2m}+V}_{\mathcal{H}_{0}} \underbrace{-\frac{e}{2mc}\left(\vec{p}\cdot\vec{A}+ \vec{A}\cdot\vec{p} \right)+\frac{e^{2}}{2mc^{2}}A^{2}+e\phi}_{\mathcal{H}_{int}} }
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{0}} is the Hamiltonian without external fields (say hydrogen atom) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{int}} is the interaction part with the radiation.
Example: electron on helium surface
Hamiltonian of Multiple Particles in Presence of Radiation
If we have a system of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N \!} particles we have the following Hamiltonian
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}=\sum_{i=1}^N \frac{\left[\vec{p}_{i}-\frac{e_{i}}{c}\vec{A}(\vec{r}_{i},t)\right]^{2}}{2m_{i}} +\sum_{i=1}^N e_{i}\phi(\vec{r}_{i},t) + V(\vec{r}_{1}...\vec{r}_{N}) }
(Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_i } are the charge and the mass of the i-th particle respectively and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}_i } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p}_i } are its coordinate and momentum operators.)
Let's assume all particles having same mass and same charge. Then we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathcal{H}&=\sum_{i=1}^N \left[\frac{\vec{p}_{i}^{2}}{2m}-\frac{e_{i}}{2mc}\left(\vec{p}_{i} \cdot \vec{A}(\vec{r}_{i},t)+\vec{A}(\vec{r}_{i},t) \cdot \vec{p}_{i} \right) + \frac{e^{2}}{2mc^{2}} \vec{A}(\vec{r}_{i},t)^{2}\right] +e\sum_{i=1}^N \phi(\vec{r}_{i},t) + V(\vec{r}_{1}...\vec{r}_{N})\\ &=\underbrace{\sum_{i=1}^N \frac{\vec{p}_{i}^{2}}{2m} + V(\vec{r}_{1}...\vec{r}_{N})}_{\mathcal{H}_{0}} \\ &{\;\;\;\;}\underbrace{+\sum_{i=1}^N -\frac{e}{2mc}\left(\vec{p}_{i} \cdot \vec{A}(\vec{r}_{i},t)+\vec{A}(\vec{r}_{i},t)\cdot \vec{p}_{i} \right) +\sum_{i=1}^N \frac{e^{2}}{2mc^{2}} \vec{A}(\vec{r}_{i},t)^{2} +e\sum_{i=1}^N \phi(\vec{r}_{i},t)}_{\mathcal{H}_{int}} \end{align}}
Using delta function operator we can write
Then
COMMENTS
- can be interpreted as the particle density operator.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{j}(\vec{r})}
is called paramagnetic current. It is just a piece of the total current Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}(\vec{r})}
.
Explicitly we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \vec{J}(\vec{r})&=\sum_{i=1}^N \frac{1}{2}\left[\vec{v}_{i}(\vec{p}_{i},\vec{r}_{i})\delta (\vec{r}-\vec{r}_{i}) + \delta (\vec{r}-\vec{r}_{i})\vec{v}_{i}(\vec{p}_{i},\vec{r}_{i}) \right]\;\;\;\leftarrow\;\;\;\vec{v}_{i}(\vec{p}_{i},\vec{r}_{i})=\frac{\vec{p}_{i}}{m}-\frac{e}{mc}\vec{A}(\vec{r}_{i},t)\\ &=\sum_{i=1}^N \frac{1}{2}\left[\frac{\vec{p}_{i}}{m}\delta (\vec{r}-\vec{r}_{i}) + \delta (\vec{r}-\vec{r}_{i})\frac{\vec{p}_{i}}{m}-\frac{2e}{mc} \vec{A}(\vec{r}_{i},t)\delta (\vec{r}-\vec{r}_{i})\right]\\ &=\vec{j}(\vec{r})-\frac{e}{mc}\sum_{i=1}^N \vec{A}(\vec{r}_{i},t)\delta (\vec{r}-\vec{r}_{i})\;\;\;\leftarrow\;\;\;\vec{A}(\vec{r}_{i},t)\delta (\vec{r}-\vec{r}_{i})=\vec{A}(\vec{r},t)\delta (\vec{r}-\vec{r}_{i})\\ &=\underbrace{\vec{j}(\vec{r})}_{paramagnetic}\underbrace{-\frac{e}{mc} \vec{A}(\vec{r},t) \rho (\vec{r})}_{diamagnetic} \end{align}}
Light Absorption and Induced Emmission
Generally for atomic fields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{j}(\mathbf{r})\cdot \mathbf{A}(\mathbf{r},t)>>\rho \mathbf{A}^{2}} . Using the transverse gauge we can approximate the interaction Hamiltonian as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_{int}= \int d^{3}\mathbf{r}\; \left[-\frac{e}{c} \mathbf{j}(\mathbf{r})\cdot \mathbf{A}(\mathbf{r},t)\right] }
Let's write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A}(\mathbf{r},t)} using the Fourier expansion as described above:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{H}_{int}&=- \int d^{3}\mathbf{r}\; \left[\frac{e}{c} \mathbf{j}(\mathbf{r}) \cdot \sum_{\mathbf{k}\boldsymbol{\lambda}} \sqrt{\frac{2\pi \hbar c^{2}}{\omega_{\mathbf{k}}}}\left[\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}} \boldsymbol{\lambda}\frac{e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}+\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger} \boldsymbol{\lambda}^{*} \frac{e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}}{\sqrt{V}}\right]\right]\\ &=-\sum_{\mathbf{k}\boldsymbol{\lambda}} e\sqrt{\frac{2\pi \hbar }{\omega_{\mathbf{k}}V}}\int d^{3}\mathbf{r}\; \mathbf{j}(\mathbf{r})\cdot \left[ \mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}} \boldsymbol{\lambda}e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)}+\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger} \boldsymbol{\lambda}^{*} e^{-i(\mathbf{k}\cdot\mathbf{r}-\omega t)}\right]\\ &=-\sum_{\mathbf{k}\boldsymbol{\lambda}} e\sqrt{\frac{2\pi \hbar }{\omega_{\mathbf{k}}V}} \left[ \mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\underbrace{\left[\int d^{3}\mathbf{r}\; \mathbf{j}(\mathbf{r})e^{i\mathbf{k}\cdot\mathbf{r}} \right]}_{\mathbf{j}_{-\mathbf{k}}}\cdot \boldsymbol{\lambda}e^{-\omega t}+\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\underbrace{\left[\int d^{3}\mathbf{r}\; \mathbf{j}(\mathbf{r})e^{-i\mathbf{k}\cdot\mathbf{r}} \right]}_{\mathbf{j}_{\mathbf{k}}}\cdot \boldsymbol{\lambda}^{*} e^{\omega t}\right]\\ &=-\sum_{\mathbf{k}\boldsymbol{\lambda}} e\sqrt{\frac{2\pi \hbar }{\omega_{\mathbf{k}}V}} \left[ \mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}e^{-\omega t}+\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*} e^{\omega t}\right]\\ \end{align}}
Where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{j}_{\mp\mathbf{k}} &=\int d^{3}\mathbf{r}\; \mathbf{j}(\mathbf{r})e^{\pm i\mathbf{k}\cdot\mathbf{r}}\\ &=\int d^{3}\mathbf{r}\; \frac{1}{2}\sum_{i} \left[\frac{\boldsymbol{p_{i}}}{m}\delta(\boldsymbol{r}-\boldsymbol{r_{i}})+\delta(\boldsymbol{r}-\boldsymbol{r_{i}})\frac{\boldsymbol{p_{i}}}{m}\right] e^{\pm i\mathbf{k}\cdot\mathbf{r}}\\ &=\frac{1}{2m} \sum_{i} \left[\frac{\boldsymbol{p_{i}}}{m}\left(\int d^{3}\mathbf{r}\;\delta(\boldsymbol{r}-\boldsymbol{r_{i}})e^{\pm i\mathbf{k}\cdot\mathbf{r}}\right)+\left(\int d^{3}\mathbf{r}\;\delta(\boldsymbol{r}-\boldsymbol{r_{i}})e^{\pm i\mathbf{k}\cdot\mathbf{r}} \right) \frac{\boldsymbol{p_{i}}}{m}\right] \\ &=\frac{1}{2m} \sum_{i} \left[\frac{\boldsymbol{p_{i}}}{m}e^{\pm i\mathbf{k}\cdot\mathbf{r}_{i}}+e^{\pm i\mathbf{k}\cdot\mathbf{r}_{i}}\frac{\boldsymbol{p_{i}}}{m}\right]\\ \end{align}}
Let's use golden rule to calculate transition rates for this time-dependent interaction. The evolution of the state in first approximation is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |\psi(t)\rangle = |I\rangle+\frac{1}{i\hbar}\int^{t}_{t_{o}}dt'\;e^{\frac{i}{\hbar}\mathbf{H}_{o}t'}\mathbf{H}_{int}e^{\eta t'}e^{-\frac{i}{\hbar}\mathbf{H}_{o}t'}|I\rangle \end{align}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |I\rangle} is the initial state and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\eta t'}} is the usual slow "switch" factor. The transition amplitude to a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F\rangle} is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle F|\psi(t)\rangle = \langle F|I\rangle+\frac{1}{i\hbar}\int^{t}_{t_{o}}dt'\;\langle F|e^{\frac{i}{\hbar}\mathbf{H}_{o}t'}\mathbf{H}_{int}e^{\eta t'}e^{-\frac{i}{\hbar}\mathbf{H}_{o}t'}|I\rangle \end{align}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F\rangle} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |I\rangle} are eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_{o}} . Then we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle F|\psi(t)\rangle &=\frac{1}{i\hbar}\int^{t}_{t_{o}}dt'\;e^{[\frac{i}{\hbar}(E_{n}-E_{o})+\eta ]t'}\langle F|\mathbf{H}_{int}|I\rangle\\ &=\frac{1}{i\hbar}\int^{t}_{t_{o}}dt'\;e^{[\frac{i}{\hbar}(E_{n}-E_{o})+\eta ]t'}\langle F| -\sum_{\mathbf{k}\boldsymbol{\lambda}} e\sqrt{\frac{2\pi \hbar }{\omega_{\mathbf{k}}V}}\cdot \left[ \mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}e^{-\omega t'}+\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*} e^{\omega t'}\right]|I\rangle\\ &=\frac{-1}{i\hbar}\sum_{\mathbf{k}\boldsymbol{\lambda}} e\sqrt{\frac{2\pi \hbar }{\omega V}} \left[ \left[\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|I\rangle \int^{t}_{t_{o}=\infin}dt'\;e^{[\frac{i}{\hbar}(E_{n}-E_{o}-\hbar \omega )+\eta ]t'} \right]+ \left[\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|I\rangle \int^{t}_{t_{o}=\infin}dt'\;e^{[\frac{i}{\hbar}(E_{n}-E_{o}+\hbar \omega )+\eta ]t'} \right] \right]\\ &=\frac{-1}{i\hbar}\sum_{\mathbf{k}\boldsymbol{\lambda}} e\sqrt{\frac{2\pi \hbar }{\omega V}} \left[ \left[\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|I\rangle \frac{e^{[\frac{i}{\hbar}(E_{n}-E_{o}-\hbar \omega )+\eta ]t}}{\frac{i}{\hbar}(E_{n}-E_{o}-\hbar \omega )+\eta } \right]+ \left[\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|I\rangle \frac{e^{[\frac{i}{\hbar}(E_{n}-E_{o}+\hbar \omega )+\eta ]t}}{\frac{i}{\hbar}(E_{n}-E_{o}+\hbar \omega )+\eta } \right] \right]\\ &=\sum_{\mathbf{k}\boldsymbol{\lambda}} e\sqrt{\frac{2\pi \hbar }{\omega V}} \left[ \left[\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|I\rangle \frac{e^{[\frac{i}{\hbar}(E_{n}-E_{o}-\hbar \omega )+\eta ]t}}{(E_{n}-E_{o}-\hbar \omega )-i\eta \hbar } \right]+ \left[\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|I\rangle \frac{e^{[\frac{i}{\hbar}(E_{n}-E_{o}+\hbar \omega )+\eta ]t}}{(E_{n}-E_{o}+\hbar \omega )-i\eta\hbar } \right] \right]\\ \end{align}}
The transition probability is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} P_{0 \rightarrow n}&=|\langle F|\psi(t)\rangle|^{2}\\ &=\sum_{\mathbf{k}\boldsymbol{\lambda}} e^{2}\frac{2\pi \hbar }{\omega V} \left[ \left[|\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|I\rangle|^{2} \frac{e^{2 \eta t}}{(E_{n}-E_{o}-\hbar \omega )^{2}+\eta^{2} \hbar^{2} } \right]+ \left[\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|I\rangle \frac{e^{2 \eta t}}{(E_{n}-E_{o}+\hbar \omega )^{2}+\eta^{2} \hbar^{2}} \right] \right]\\ \end{align}}
Where all oscillatory terms have been averaged to zero. Taking a time derivative we obtain the transition rate
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \Gamma_{0 \rightarrow n}&=\frac{dP_{0 \rightarrow n}}{dt}\\ &=\sum_{\mathbf{k}\boldsymbol{\lambda}} e^{2}\frac{2\pi \hbar }{\omega V} \left[ \left[|\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|I\rangle|^{2} \frac{2 \eta e^{2 \eta t}}{(E_{n}-E_{o}-\hbar \omega )^{2}+\eta^{2} \hbar^{2} } \right]+ \left[|\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|I\rangle |^{2} \frac{2 \eta e^{2 \eta t}}{(E_{n}-E_{o}+\hbar \omega )^{2}+\eta^{2} \hbar^{2}} \right] \right]\\ &\overset{\underset{\mathrm{\eta \rightarrow 0 }}{}}{=}\sum_{\mathbf{k}\boldsymbol{\lambda}} e^{2}\frac{2\pi \hbar }{\omega V} \left[ \left[|\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|I\rangle|^{2} \frac{2\pi}{\hbar}\delta (E_{n}-E_{o}-\hbar \omega) \right]+ \left[|\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|I\rangle |^{2} \frac{2\pi}{\hbar}\delta (E_{n}-E_{o}+\hbar \omega) \right] \right]\\ &=\sum_{\mathbf{k}\boldsymbol{\lambda}} \frac{4\pi^{2} e^{2} }{\omega V} \left[ \left[|\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|I\rangle|^{2} \delta (E_{n}-E_{o}-\hbar \omega) \right]+ \left[|\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|I\rangle|^{2} \delta (E_{n}-E_{o}+\hbar \omega) \right] \right]\\ &=\sum_{\mathbf{k}\boldsymbol{\lambda}} \left[ \underbrace{ \left[\frac{4\pi^{2} e^{2} }{\omega V}|\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|I\rangle|^{2} \delta (E_{n}-E_{o}-\hbar \omega) \right] }_{\Gamma^{abs}_{0 \rightarrow n;\mathbf{k}\boldsymbol{\lambda}} } + \underbrace{ \left[\frac{4\pi^{2} e^{2} }{\omega V}|\langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|I\rangle|^{2} \delta (E_{n}-E_{o}+\hbar \omega) \right] }_{\Gamma^{ind.em}_{n \rightarrow 0;\mathbf{k}\boldsymbol{\lambda}} } \right]\\ &=\sum_{\mathbf{k}\boldsymbol{\lambda}} \left[\Gamma^{abs}_{0 \rightarrow n;\mathbf{k}\boldsymbol{\lambda}}+ \Gamma^{ind.em}_{n \rightarrow 0;\mathbf{k}\boldsymbol{\lambda}}\right]\\ \end{align}}
The above equation says that the transition rate between two states is composed by two possibilities: absorption Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma^{abs}_{0 \rightarrow n;\mathbf{k}\boldsymbol{\lambda}}} or induced emission Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma^{ind.em}_{n \rightarrow 0;\mathbf{k}\boldsymbol{\lambda}}} . Let's analyze the matrix elements between states.
Absorption
Let's suppose that initial and final states are:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |I\rangle&=|o\rangle \otimes |N_{1\boldsymbol{\lambda}},...,N_{K\boldsymbol{\lambda}},...\rangle \\ |F\rangle&=|n\rangle \otimes |N_{1\boldsymbol{\lambda}},...,M_{K\boldsymbol{\lambda}},...\rangle \\ \end{align}}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {|o\rangle, |n\rangle}} are the initial and final states of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_{0}} (say hydrogen atom) with energies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}<E_{n}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {|N_{1\boldsymbol{\lambda}},...,N_{K\boldsymbol{\lambda}},...\rangle, |N_{1\boldsymbol{\lambda}},...,M_{K\boldsymbol{\lambda}},...\rangle}} are the initial and final states of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_{rad}} (the vacuum).
The matrix element of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma^{abs}_{0 \rightarrow n;\mathbf{k}\boldsymbol{\lambda}}} isgiven by:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|I\rangle &=\langle n|\otimes \langle N_{1\boldsymbol{\lambda}},...,M_{K\boldsymbol{\lambda}},...|\left[\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}\right]|0\rangle \otimes |N_{1\boldsymbol{\lambda}},...,N_{K\boldsymbol{\lambda}},...\rangle\\ &=\langle n|\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|0\rangle \langle N_{1\boldsymbol{\lambda}},...,M_{K\boldsymbol{\lambda}},...|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}|N_{1\boldsymbol{\lambda}},...,N_{K\boldsymbol{\lambda}},...\rangle\\ &=\langle n|\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|0\rangle \langle M_{K\boldsymbol{\lambda}}|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}|N_{K\boldsymbol{\lambda}}\rangle\\ &=\langle n|\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|0\rangle \sqrt{N_{K\boldsymbol{\lambda}}}\langle M_{K\boldsymbol{\lambda}}|N_{K\boldsymbol{\lambda}}-1\rangle\\ &=\langle n|\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|0\rangle \sqrt{N_{K\boldsymbol{\lambda}}}\delta_{M_{K\boldsymbol{\lambda}},N_{K\boldsymbol{\lambda}}-1}\\ \end{align}}
The last shows how in the absorption process, the system Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_{int}} absorbs a single photon from the radiation. Namely the final state is given by:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |F\rangle&=|n\rangle \otimes |N_{1\boldsymbol{\lambda}},...,N_{K\boldsymbol{\lambda}}-1,...\rangle \\ \end{align}}
Finally we can write the transition rate absorption as following
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \Gamma^{abs}_{0 \rightarrow n;\mathbf{k}\boldsymbol{\lambda}} &=\frac{4\pi^{2} e^{2} }{\omega V}|\langle n|\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|0\rangle \sqrt{N_{K\boldsymbol{\lambda}}}|^{2} \delta (E_{n}-E_{o}-\hbar \omega)\\ &=\frac{4\pi^{2} e^{2} }{\omega V}|\langle n|\mathbf{j}_{-\mathbf{k}}\cdot \boldsymbol{\lambda}|0\rangle |^{2}N_{K\boldsymbol{\lambda}} \delta (E_{n}-E_{o}-\hbar \omega) \end{align}}
Induced Emission
Let's suppose that initial and final states are:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |I\rangle&=|n\rangle \otimes |N_{1\boldsymbol{\lambda}},...,N_{K\boldsymbol{\lambda}},...\rangle \\ |F\rangle&=|0\rangle \otimes |N_{1\boldsymbol{\lambda}},...,M_{K\boldsymbol{\lambda}},...\rangle \\ \end{align}}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {|n\rangle, |0\rangle}} are the initial and final states of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_{0}} (say hydrogen atom) with energies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}<E_{n}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {|N_{1\boldsymbol{\lambda}},...,N_{K\boldsymbol{\lambda}},...\rangle, |N_{1\boldsymbol{\lambda}},...,M_{K\boldsymbol{\lambda}},...\rangle}} are the initial and final states of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_{rad}} (the vacuum).
The matrix element of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma^{ind.em}_{0 \rightarrow n;\mathbf{k}\boldsymbol{\lambda}}} isgiven by:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle F|\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|I\rangle &=\langle 0|\otimes \langle N_{1\boldsymbol{\lambda}},...,M_{K\boldsymbol{\lambda}},...|\left[\mathbf{a}_{\mathbf{k}\boldsymbol{\lambda}}^{\dagger}\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}\right]|n\rangle \otimes |N_{1\boldsymbol{\lambda}},...,N_{K\boldsymbol{\lambda}},...\rangle\\ &=\langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle \langle N_{1\boldsymbol{\lambda}},...,M_{K\boldsymbol{\lambda}},...|\mathbf{a}^{\dagger}_{\mathbf{k}\boldsymbol{\lambda}}|N_{1\boldsymbol{\lambda}},...,N_{K\boldsymbol{\lambda}},...\rangle\\ &=\langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle \langle M_{K\boldsymbol{\lambda}}|\mathbf{a}^{\dagger}_{\mathbf{k}\boldsymbol{\lambda}}|N_{K\boldsymbol{\lambda}}\rangle\\ &=\langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle \sqrt{N_{K\boldsymbol{\lambda}}+1}\langle M_{K\boldsymbol{\lambda}}|N_{K\boldsymbol{\lambda}}+1\rangle\\ &=\langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle \sqrt{N_{K\boldsymbol{\lambda}}+1}\delta_{M_{K\boldsymbol{\lambda}},N_{K\boldsymbol{\lambda}}+1}\\ \end{align}}
The last shows how in the emmision process, the system Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H}_{int}} release a single photon from the radiation. Namely the final state is given by:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |F\rangle&=|0\rangle \otimes |N_{1\boldsymbol{\lambda}},...,N_{K\boldsymbol{\lambda}}+1,...\rangle \\ \end{align}}
Finally we can write the transition rate absorption as following
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \Gamma^{ind.em}_{n \rightarrow 0;\mathbf{k}\boldsymbol{\lambda}} &=\frac{4\pi^{2} e^{2} }{\omega V}|\langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle \sqrt{N_{K\boldsymbol{\lambda}}+1}|^{2} \delta (E_{0}-E_{n}+\hbar \omega)\\ &=\frac{4\pi^{2} e^{2} }{\omega V}|\langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle |^{2} (N_{K\boldsymbol{\lambda}}+1) \delta (E_{n}-E_{o}-\hbar \omega) \end{align}}
Important Phenomena: Spontaneous Emission
Let's suppose that initial is a single Hydrogen atom in the 2P state in the vacuum (and nothing else!!!). The state can be written as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |I\rangle&=|2P\rangle \otimes |0,...,0,...\rangle \\ \end{align}}
According to induced emission, there could be a process in which the final state is:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |F\rangle&=|1S\rangle \otimes |0,...,1,...\rangle \\ \end{align}}
Where a single photon has been emitted without any external perturbation. This is emission process is called Spontaneous emission. For an experimental observation of a Lamb-like shift in a solid state setup see here.
Einstein's Model of Absorption and Induced Emmision
Let's use Statistical Mechanics to study a cavity with radiation. For this we need to use the Plank distribution:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle N_{\boldsymbol{k}\boldsymbol{\lambda}}\rangle=\frac{1}{e^{\frac{\hbar c k}{K_{B}T}}-1} \end{align}}
This is just the occupation number of the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{k}\boldsymbol{\lambda}} . Let's suppose the following situation:
- Our cavity is made up with atoms with two quantum levels with energies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n}>E_{0}} .
- The walls are emitting and absorbing radiation (Thermal Radiation) such that system is at equilibrium. Since there is just two levels, the photons emitted by atoms must have energy equal to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n}-E_{0}} .
The Boltzmann distribution tells us that the probabilities to find atoms at energies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}} are respectively
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} P_{n}=\frac{1}{Q}e^{-\frac{E_{n}}{K_{B}T}}\\ P_{0}=\frac{1}{Q}e^{-\frac{E_{0}}{K_{B}T}}\\ \end{align}}
Let's call Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle N \rangle } the number of photons at equilibrium. At equilibrium we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} 0&=\frac{dN}{dt}\\ 0&=\left(\frac{dN}{dt}\right)_{abs}+\left(\frac{dN}{dt}\right)_{ind.em} \end{align}}
It is natural to express the absorption and emission rate as:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \left(\frac{dN}{dt}\right)_{abs}&=-BNP_{0}\\ \left(\frac{dN}{dt}\right)_{ind.em}&=BNP_{n} \end{align}}
Where B is some constant. Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{n}<P_{0}} we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\left(\frac{dN}{dt}\right)\right|_{abs}>\left|\left(\frac{dN}{dt}\right)\right|_{ind.em}}
This means that eventually all photons will be absorbed and then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle N \rangle =0} . This of course is not a physical situation. Einstein realized that there is another kind of process of emission that balances the rates in such way that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle N \rangle \ne 0} . This emission is precisely the spontaneous emission and can be written as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \left(\frac{dN}{dt}\right)_{spon.em}&=AP_{n} \end{align}}
Then we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} 0&=\left(\frac{dN}{dt}\right)_{abs}+\left(\frac{dN}{dt}\right)_{ind.em}+\left(\frac{dN}{dt}\right)_{spon.em}\\ 0&=-BNP_{0}+BNP_{n}+AP_{n}\\ \end{align}}
And solving for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A } we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} A&=B \langle N \rangle \left(e^{\frac{E_{n}-E_{0}}{K_{B}T}}-1\right)\\ &=B \langle N \rangle \frac{1}{ \langle N \rangle }\\ &=B \end{align}}
As conclusion we obtain for the emission rate the follwing:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \left(\frac{dN}{dt}\right)_{emission}&=\left(\frac{dN}{dt}\right)_{ind.em}+\left(\frac{dN}{dt}\right)_{spon.em}\\ &=BNP_{n}+AP_{n}\\ &=BP_{n}(N+1)\\ \end{align}}
Notice that the factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (N+1)} matches with our previous result.
Details of Spontaneous Emission
Power of the emitted light
Using our previous result for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma^{spon.em}_{n \rightarrow 0;\mathbf{k}\boldsymbol{\lambda}}} , we can calculate the power Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dP} of the light with polarization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\lambda}} per unit of solid angle that the spontaneus emission produce:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} dP&=\sum_{k}\hbar \omega \;\Gamma^{spon.em}_{n \rightarrow 0;\mathbf{k}\boldsymbol{\lambda}}\\ &=d\Omega V \int \frac{dk\;k^{2}}{(2\pi)^{3}}\;\hbar \omega \;\Gamma^{spon.em}_{n \rightarrow 0;\mathbf{k}\boldsymbol{\lambda}}\\ &=d\Omega V \int \frac{d\omega\;\omega^{2}}{(2\pi c)^{3}}\;\hbar \omega \;\Gamma^{spon.em}_{n \rightarrow 0;\mathbf{k}\boldsymbol{\lambda}}\\ \end{align} }
Then
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{dP}{d\Omega} &=V \int\frac{d\omega\;\omega^{2}}{(2\pi c)^{3}}\;\hbar \omega \left[ \frac{4\pi^{2} e^{2} }{\omega V}|\langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle|^{2} \delta (E_{n}-E_{0}-\hbar \omega) \right]\\ &=\frac{e^{2}\hbar}{2\pi c^{3}}|\langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle|^{2}\int d\omega\;\omega^{2} \delta (E_{n}-E_{0}-\hbar \omega)\\ &=\frac{e^{2}\hbar}{2\pi c^{3}}|\langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle|^{2}\frac{(E_{n}-E_{0})^{2}}{\hbar^{3}}\;\;\;\leftarrow\;\;\;\hbar\omega_{n,0}=E_{n}-E_{0}\\ &=\frac{e^{2}\omega^{2}_{n,0}}{2\pi c^{3}}|\langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle|^{2}\\ \end{align} }
Conservation of Momentum
Consider a matter in the eigenstate of the momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar q_{n}} . Suppose that it make a transition to eigenstate with momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar q_{0}} via spontaneus emission. The momentum must conserve. Therefore we have a process where:
Initial MomentaFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\;\;\rightarrow\;\;\;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}matter& \rightarrow \hbar q_{n}\\vacuum& \rightarrow 0\end{align}}
Final MomentaFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\;\;\rightarrow\;\;\;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}matter& \rightarrow \hbar q_{0}\\vacuum& \rightarrow \hbar q_{n}-\hbar q_{0}\end{align}}
Let's calculate the matrix element Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \mathbf{q_{0}}|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|\mathbf{q_{n}}\rangle}
for two cases.
Case 1: Single free charged particle
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle \mathbf{q_{0}}|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|\mathbf{q_{n}}\rangle &=\boldsymbol{\lambda}^{*}\cdot\langle \mathbf{q_{0}}|\mathbf{j}_{\mathbf{k}}|\mathbf{q_{n}}\rangle\\ &=\boldsymbol{\lambda}^{*}\cdot\left\langle \mathbf{q_{0}}\left|\frac{1}{2} \left[\frac{\boldsymbol{p_{i}}}{m}e^{- i\mathbf{k}\cdot\mathbf{r}_{i}}+e^{- i\mathbf{k}\cdot\mathbf{r}_{i}}\frac{\boldsymbol{p_{i}}}{m}\right]\right|\mathbf{q_{n}}\right\rangle\\ &=\boldsymbol{\lambda}^{*}\cdot\frac{1}{2}\left\langle \mathbf{q_{0}}\left| \left[\frac{\hbar \mathbf{q_{0}}}{m}e^{- i\mathbf{k}\cdot\mathbf{r}_{i}}+e^{- i\mathbf{k}\cdot\mathbf{r}_{i}}\frac{\hbar \mathbf{q_{n}}}{m}\right]\right|\mathbf{q_{n}}\right\rangle\\ &=\boldsymbol{\lambda}^{*}\cdot\frac{\hbar (\mathbf{q_{0}}+\mathbf{q_{n}})}{2m}\langle \mathbf{q_{0}}| e^{- i\mathbf{k}\cdot\mathbf{r}_{i}}|\mathbf{q_{n}}\rangle\\ &=\boldsymbol{\lambda}^{*}\cdot\frac{\hbar (\mathbf{q_{0}}+\mathbf{q_{n}})}{2m} \int d^{3}r_{i} \langle \mathbf{q_{0}}|\mathbf{r}_{i}\rangle \langle \mathbf{r}_{i}| e^{-i\mathbf{k}\cdot\mathbf{r}_{i}}|\mathbf{q_{n}}\rangle\\ &=\boldsymbol{\lambda}^{*}\cdot\frac{\hbar (\mathbf{q_{0}}+\mathbf{q_{n}})}{2m} \int d^{3}r_{i} e^{-i\mathbf{q_{0}}\cdot\mathbf{r}_{i}} e^{-i\mathbf{k}\cdot\mathbf{r}_{i}} e^{i\mathbf{q_{n}}\cdot\mathbf{r}_{i}}\\ &=\boldsymbol{\lambda}^{*}\cdot\frac{\hbar (\mathbf{q_{0}}+\mathbf{q_{n}})}{2m} \delta(\mathbf{q_{n}}-\mathbf{q_{0}}-\mathbf{k}) \\ \end{align} }
This result is very interesting!!!. It says that the emitted light must be
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \hbar \mathbf{k} =\hbar \mathbf{q_{n}} -\hbar \mathbf{q_{0}} \end{align} }
However this is impossible from the point of view of conservation of energy:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \hbar c k =\frac{\hbar q^{2}_{n}}{2m}-\frac{\hbar q^{2}_{0}}{2m} \end{align} }
This means that a single charged particle can not make transitions. So a single charged particle doesn't see the vacuum fluctuations.
Case 2: General Case (System of particles)
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle \mathbf{q_{0}}|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|\mathbf{q_{n}}\rangle &=\boldsymbol{\lambda}^{*}\cdot\langle \mathbf{q_{0}}|\mathbf{j}_{\mathbf{k}}|\mathbf{q_{n}}\rangle\\ &=\boldsymbol{\lambda}^{*}\cdot\left\langle \mathbf{q_{0}}\left|\int d^{3}r j(\mathbf{r}) e^{-i\mathbf{k}\cdot\mathbf{r}}\right|\mathbf{q_{n}}\right\rangle\\ &=\boldsymbol{\lambda}^{*}\cdot\int d^{3}r \langle \mathbf{q_{0}}|j(\mathbf{r})|\mathbf{q_{n}}\rangle e^{-i\mathbf{k}\cdot\mathbf{r}}\\ \end{align} }
We can use the total momentum of the system Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{P}=\sum_{i}\mathbf{p}_{i}} as generator of translations for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}} . So that we can write
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} j(\mathbf{r})=e^{-\frac{i}{\hbar}\mathbf{P}\cdot\mathbf{r}}j(\mathbf{r}=0)e^{\frac{i}{\hbar}\mathbf{P}\cdot\mathbf{r}} \end{align} }
Then
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle \mathbf{q_{0}}|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|\mathbf{q_{n}}\rangle &=\boldsymbol{\lambda}^{*}\cdot\int d^{3}r \langle \mathbf{q_{0}}|j(\mathbf{r})|\mathbf{q_{n}}\rangle e^{-i\mathbf{k}\cdot\mathbf{r}}\\ &=\boldsymbol{\lambda}^{*}\cdot\int d^{3}r \langle \mathbf{q_{0}}|e^{-\frac{i}{\hbar}\mathbf{P}\cdot\mathbf{r}}j(0)e^{\frac{i}{\hbar}\mathbf{P}\cdot\mathbf{r}}|\mathbf{q_{n}}\rangle e^{-i\mathbf{k}\cdot\mathbf{r}}\\ &=\boldsymbol{\lambda}^{*}\cdot\int d^{3}r \langle \mathbf{q_{0}}|e^{-i\mathbf{q_{0}}\cdot\mathbf{r}}j(0)e^{i\mathbf{q_{n}}\cdot\mathbf{r}}|\mathbf{q_{n}}\rangle e^{-i\mathbf{k}\cdot\mathbf{r}}\\ &=\boldsymbol{\lambda}^{*}\cdot \langle \mathbf{q_{0}}|j(0)|\mathbf{q_{n}}\rangle\int d^{3}r e^{i\mathbf{q_{n}}\cdot\mathbf{r}} e^{-i\mathbf{q_{0}}\cdot\mathbf{r}} e^{-i\mathbf{k}\cdot\mathbf{r}}\\ &=\boldsymbol{\lambda}^{*}\cdot \langle \mathbf{q_{0}}|j(0)|\mathbf{q_{n}}\rangle\delta(\mathbf{q_{n}}-\mathbf{q_{0}}-\mathbf{k})\\ \end{align} }
The last shows that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \hbar \mathbf{k} =\hbar \mathbf{q_{n}} -\hbar \mathbf{q_{0}} \end{align} }
Electric Dipole Transitions
Let's consider a nucleus (say hydrogen atom) well localized in space. Typically the wave length of the emitted light is much bigger than electron's orbit around nucleus (say Bohr radius Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{B}} ). For example the wavelength of blue light is on the order of 100 nm or 1000 Angstrom, while the wavelength of the electron orbiting the nucleus in the Hydrogen atom is of the order of 1 Angstrom. This means that:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\;\;\;\lambda >>> a_{B}\;\;\;\;\leftrightarrow\;\;\;\;\;\mathbf{k}<<<1}
The matrix element is then
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle &=\mathbf{\lambda}^{*}\cdot\langle 0|\mathbf{j}_{\mathbf{k}}|n\rangle\\ &=\mathbf{\lambda}^{*}\cdot\int d^{3}\mathbf{r}\;e^{-i\mathbf{k}\cdot\mathbf{r}} \langle 0|\mathbf{j}(\mathbf{r})|n\rangle\\ &=\mathbf{\lambda}^{*}\cdot\int d^{3}\mathbf{r}\;e^{-i\mathbf{k}\cdot\mathbf{r}} \langle 0|\mathbf{j}(\mathbf{r})|n\rangle\\ &=\mathbf{\lambda}^{*}\cdot\int d^{3}\mathbf{r}\;\left[1-i\mathbf{k}\cdot\mathbf{r}+...\right] \langle 0|\mathbf{j}(\mathbf{r})|n\rangle\\ &\cong\mathbf{\lambda}^{*}\cdot\int d^{3}\mathbf{r}\;\langle 0|\mathbf{j}(\mathbf{r})|n\rangle\\ &\cong\mathbf{\lambda}^{*}\cdot\int d^{3}\mathbf{r}\;\langle 0|\frac{1}{2}\left[\sum_{i} \frac{\mathbf{p}_{i}}{m} \delta(\mathbf{r}-\mathbf{r}_{i})+\delta(\mathbf{r}-\mathbf{r}_{i})\frac{\mathbf{p}_{i}}{m}\right]|n\rangle\\ &\cong\mathbf{\lambda}^{*}\cdot\langle 0|\sum_{i} \frac{\mathbf{p}_{i}}{m}|n\rangle\\ &\cong\mathbf{\lambda}^{*}\cdot\langle 0|\frac{\mathbf{P}}{m}|n\rangle\;\;\;\;\;\;\; \leftarrow\;\;\;\;\;\frac{\mathbf{P}}{m}=\frac{[\mathbf{R},\mathbf{H}_{0}]}{i\hbar}\\ &\cong\mathbf{\lambda}^{*}\cdot\frac{1}{i\hbar}\langle 0|[\mathbf{R}\cdot \mathbf{H}_{0}-\mathbf{H}_{0}\cdot\mathbf{R}]|n\rangle\\ &\cong\mathbf{\lambda}^{*}\cdot\frac{1}{i\hbar}\langle 0|[\mathbf{R}E_{n}-E_{0}\mathbf{R}]|n\rangle\\ &\cong\mathbf{\lambda}^{*}\cdot\frac{E_{n}-E_{0}}{i\hbar}\langle 0|\mathbf{R}|n\rangle\\ &\cong\mathbf{\lambda}^{*}\cdot\frac{\hbar\omega_{n,0}}{i\hbar}\langle 0|\mathbf{R}|n\rangle\\ &\cong\mathbf{\lambda}^{*}\cdot\frac{\omega_{n,0}}{i}\underbrace{\langle 0|\mathbf{R}|n\rangle}_{\mathbf{d}_{0,n}}\\ &\cong\frac{\omega_{n,0}}{i}\mathbf{d}_{0,n}\cdot\mathbf{\lambda}^{*}\\ \end{align}}
Notice that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{d}_{0,n}} is the off diagonal elements of the dipole moment operator. The power per unit of solid angle for a given polarization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{dP}{d\Omega} &=\frac{e^{2}\omega^{2}_{n,0}}{2\pi c^{3}}|\langle 0|\mathbf{j}_{\mathbf{k}}\cdot \boldsymbol{\lambda}^{*}|n\rangle|^{2}\\ &\cong\frac{e^{2}\omega^{2}_{n,0}}{2\pi c^{3}}\left|\frac{\omega_{n,0}}{i}\mathbf{d}_{0,n}\cdot\mathbf{\lambda}^{*}\right|^{2}\\ &\cong\frac{e^{2}\omega^{4}_{n,0}}{2\pi c^{3}}\left|\mathbf{d}_{0,n}\cdot\mathbf{\lambda}^{*}\right|^{2}\\ \end{align}}
Selection Rules
Let's assume that initial and final states are eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{L}^{2}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{L}_{z}} . Using commutation relationships we can obtain the following selection rules the vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{d}_{0,n}} :
1. Selection Rules for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m}
1.1Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\mathbf{L}_{z},\mathbf{R}_{z}]=0} . From this we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} 0&=\langle l' m' |[\mathbf{L}_{z},\mathbf{R}_{z}]| l m \rangle\\ &=\langle l' m' |\mathbf{L}_{z} \mathbf{R}_{z} - \mathbf{L}_{z}\mathbf{R}_{z}| l m \rangle\\ &=\hbar(m'-m)\langle l' m' |\mathbf{R}_{z}| l m \rangle\\ \end{align}}
This means that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle l' m' |\mathbf{R}_{z}| l m \rangle=0} if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m'-m\neq 0} .
1.2
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\mathbf{L}_{z},\mathbf{R}_{x}]=i\hbar\mathbf{R}_{y}}
. From this we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle l' m' |[\mathbf{L}_{z},\mathbf{R}_{x}] |l m \rangle&=i\hbar \langle l' m' |\mathbf{R}_{y}] l m \rangle\\ (m'-m)\langle l' m' |\mathbf{R}_{x}| l m \rangle&=i\langle l' m' |\mathbf{R}_{y}] l m \rangle\\ \end{align}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\mathbf{L}_{z},\mathbf{R}_{y}]=-i\hbar\mathbf{R}_{x}}
. From this we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle l' m' |[\mathbf{L}_{z},\mathbf{R}_{y}] |l m \rangle&=-i\hbar \langle l' m' |\mathbf{R}_{x}] l m \rangle\\ (m'-m)\langle l' m' |\mathbf{R}_{y}| l m \rangle&=-i\langle l' m' |\mathbf{R}_{x}] l m \rangle\\ \end{align}}
Combining
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} (m'-m)^{2}\langle l' m'|\mathbf{R}_{x}|l m \rangle=\langle l' m'|\mathbf{R}_{x}|l m \rangle\\ (m'-m)^{2}\langle l' m'|\mathbf{R}_{y}|l m \rangle=\langle l' m'|\mathbf{R}_{y}|l m \rangle\\ \end{align}}
From here we see that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} (m'-m)^{2}\langle l' m'|\mathbf{R}_{x,y}|l m \rangle&=\langle l' m'|\mathbf{R}_{x,y}|l m \rangle\\ ((m'-m)^{2}-1)\langle l' m'|\mathbf{R}_{x,y}|l m \rangle &=0\\ \end{align}}
This means that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle l' m'|\mathbf{R}_{x,y}|l m \rangle=0} if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [(m'-m)^{2}-1]\neq0 \;\;\;\;\rightarrow\;\;\;\;m'\neq m\pm 1}
2. Selection Rule for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l}
Consider the following commutator proposed by Dirac
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\mathbf{L}^{2},[\mathbf{L}^{2},\mathbf{R}]]=2\hbar ^{2}(\mathbf{R}\mathbf{L}^{2}+\mathbf{L}^{2}\mathbf{R})}
After some algebra we can see that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (l'+l)(l'+l+2)((l'-l)^{2}-1)\langle l' m'|\mathbf{R}|l m \rangle=0}
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} is non negative Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (l'+l+2)\neq0\;\;\;\;\forall\;\;\;\;l',l } . There are two possibilities:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle l' m'|\mathbf{R}|l m \rangle=0} if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (l'+l)\neq 0} . However Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (l'+l)=0} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l'=l=0} , which corresponds to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle 0 0|\mathbf{R}|0 0 \rangle=0} . This possibility is trivial and it doesn't say anything new.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle l' m'|\mathbf{R}|l m \rangle=0} if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ((l'-l)^{2}-1)\neq 0\;\;\;\;\rightarrow\;\;\;\;l'\neq l\pm 1}
Summary
If the initial and final states are eigenstates for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{L}^{2}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{L}_{z}} then the possible transitions that can occur in the dipole approximation are
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} l'&= l\pm 1\\ m'&= m\\ m'&= m\pm 1\\ \end{align}}
Example: Transitions Among Levels n=1,2,3 of Hydrogen Atom
Let's consider the levels n=1,2,3 of Hydrogen Atom. The possible transitions to the state 1S according to the sharp selection rules are the following
The possibles transitions to the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2p_0 }
are the following
Power & Polarization of Emitted Light
Case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m'=m} : In this case the selection rules tell us that:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{d}_{0,n}= \langle 0|\mathbf{R}|n\rangle= \begin{pmatrix} \langle 0|\mathbf{R}_{x}|n\rangle \\ \langle 0|\mathbf{R}_{y}|n\rangle \\ \langle 0|\mathbf{R}_{z}|n\rangle \\ \end{pmatrix} =\begin{pmatrix} 0 \\ 0 \\ \langle 0|\mathbf{R}_{z}|n\rangle \\ \end{pmatrix} \end{align}}
Then we can say
- The light is always plane polarized in the plane defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}} .
- The power is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{dP}{d\Omega} &\cong\frac{e^{2}\omega^{4}_{n,0}}{2\pi c^{3}}\left|\mathbf{d}_{0,n}\cdot\mathbf{\lambda}^{*}\right|^{2}\\ &\cong\frac{e^{2}\omega^{4}_{n,0}}{2\pi c^{3}}\left|\langle 0|\mathbf{R}_{z}|n\rangle\right|^{2}\;sin^{2}\theta\\ \end{align}}
Case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m'=m\pm 1} : In this case the selection rules tell us that:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{d}_{0,n}= \langle 0|\mathbf{R}|n\rangle= \begin{pmatrix} \langle 0|\mathbf{R}_{x}|n\rangle \\ \langle 0|\mathbf{R}_{y}|n\rangle \\ \langle 0|\mathbf{R}_{z}|n\rangle \\ \end{pmatrix} =\begin{pmatrix} \langle 0|\mathbf{R}_{x}|n\rangle \\ \langle 0|\mathbf{R}_{y}|n\rangle \\ 0 \\ \end{pmatrix} \end{align}}
From the previous result we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mp \langle l' m' |\mathbf{R}_{y}| l m \rangle&=-i\langle l' m' |\mathbf{R}_{x}] l m \rangle\\ \end{align}}
Then
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{d}_{0,n}= \langle 0|\mathbf{R}_{x}|n\rangle \begin{pmatrix} 1 \\ \pm i \\ 0 \\ \end{pmatrix} \end{align}}
Then we can say
- rest at the XY plane. The polarization of the emitted light is circular.
- Lets put a detector to see the light coming toward positive Z axis. Since right circular polarized light has angular momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar}
while negative circular polarized light has angular momentumFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\hbar}
we can state the following:
- If we see a circular polarized light then by conservation of angular momentum we know that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \hbar m=\hbar m' + \hbar^{photon}\;\;\;\;\;\rightarrow \;\;\;\;\; m'-m=-1 \end{align}}
- If we see a negative circular polarized light then by conservation of angular momentum we know that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \hbar m=\hbar m' - \hbar^{photon}\;\;\;\;\;\rightarrow \;\;\;\;\; m'-m=1 \end{align}}
Scattering of Light
( Notes and LaTex code, courtesy of Dr. Oskar Vafek)
We can analyze how a charged system interact with photons and scatter it. The problem of light scattering can be considered as a transition from initial state, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\chi_0\rangle=|0;N_{k,\lambda},N_{k',\lambda'}=0\rangle} to a final state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n;N_{k,\lambda}-1,N_{k',\lambda'}=1\rangle } . For this transition we can calculate the transition amplitude. Let us deal with some basics first. First of all we can write the Schrodinger equation for an electron in a potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)} interacting with quantized EM radiation as:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial}{\partial t}|\psi\rangle =\mathcal{H}|\psi\rangle }
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}=\frac{1}{2m}\left(p-\frac{e}{c}A(r)\right)^2+V(r)+\sum_{k,\hat{\lambda}}\hbar\omega_{k}\left(\hat{a}_{k\hat{\lambda}}^{\dagger}\hat{a}_{k\hat{\hat{\lambda}}}+\frac{1}{2}\right) }
We are considering the transverse gauge, in which the vector potential operator can be defined as: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\hat{A}(r)}=\frac{1}{\sqrt{V}}\sum_{k,\lambda}\left[\sqrt{\frac{2\pi\hbar}{\omega_{k}}}c\;\left(\hat{a}_{k,\hat{\lambda}}\hat{\lambda}e^{ik\cdot r}+\hat{a}^{\dagger}_{k,\hat{\lambda}}\hat{\lambda^*}e^{-ik\cdot r}\right)\right]}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\hat{a}_{k\hat{\lambda}},\hat{a}_{k'\hat{\lambda'}}^{\dagger}]=\delta_{kk'}\delta_{\hat{\lambda}\hat{\lambda'}};\;\;\;\; [\hat{a}_{k\hat{\lambda}},\hat{a}_{k'\hat{\lambda'}}]=0 }
Let us define,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}=\mathcal{H}_0+\mathcal{H}'}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_0=\mathcal{H}^{(at)}_0+\mathcal{H}^{(rad)}_0=\left(\frac{p^2}{2m}+V(r)\right)+\sum_{k,\hat{\lambda}}\hbar\omega_{k}\left(\hat{a}_{k\hat{\lambda}}^{\dagger}\hat{a}_{k\hat{\hat{\lambda}}}+\frac{1}{2}\right)}
andFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}'=-\frac{e}{mc}\mathbf{A(r)}\cdot p+\frac{e^2}{2mc^2}\mathbf{A(r)}\cdot \mathbf{A(r)}}
We can use the Dirac picture to represent the wavefunction as: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(t)\rangle=e^{-\frac{i}{\hbar}\mathcal{H}_0t}|\chi(t)\rangle }Therefore,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial}{\partial t}|\chi\rangle =\mathcal{H}'_I(t)|\chi\rangle =e^{\frac{i}{\hbar}\mathcal{H}_0t}\mathcal{H}'e^{-\frac{i}{\hbar}\mathcal{H}_0t}|\chi\rangle =e^{\frac{i}{\hbar}\mathcal{H}^{(at)}_0t}\left(e^{\frac{i}{\hbar}\mathcal{H}^{(rad)}_0t}\mathcal{H}' e^{-\frac{i}{\hbar}\mathcal{H}^{(rad)}_0t}\right)e^{-\frac{i}{\hbar}\mathcal{H}^{(at)}_0t}|\chi\rangle}
More precisely,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}'_I(t)= e^{\frac{i}{\hbar}\mathcal{H}^{(at)}_0t}\left(e^{\frac{i}{\hbar}\mathcal{H}^{(rad)}_0t}\mathcal{H}' e^{-\frac{i}{\hbar}\mathcal{H}^{(rad)}_0t}\right)e^{-\frac{i}{\hbar}\mathcal{H}^{(at)}_0t} =e^{\frac{i}{\hbar}\mathcal{H}^{(at)}_0t}\left( -\frac{e}{mc}A(r,t)\cdot p+\frac{e^2}{2mc^2}A(r,t)\cdot A(r,t)\right)e^{-\frac{i}{\hbar}\mathcal{H}^{(at)}_0t}}
where the vector potential operator which is now time dependent can be defined as,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A(r,t)}=\frac{1}{\sqrt{V}}\sum_{k,\lambda}\left[\sqrt{\frac{2\pi\hbar}{\omega_{k}}}c\;\left(\hat{a}_{k,\hat{\lambda}}\hat{\lambda}e^{ik\cdot r-i\omega_{k} t}+\hat{a}^{\dagger}_{k,\hat{\lambda}}\hat{\lambda^*}e^{-ik\cdot r+i\omega_{k}t}\right)\right]}
Using second order time dependent perturbation theory up to to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{nd}} order, we can write the wavefunction is Dirac picture as,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\chi(t)\rangle\approx|\chi_0\rangle+\frac{1}{i\hbar}\int_{-\infty}^{t}dt'\mathcal{H}'_I(t')|\chi_0\rangle+ \frac{1}{(i\hbar)^2}\int_{-\infty}^{t}dt'\int_{-\infty}^{t'}dt''\mathcal{H}'_I(t')\mathcal{H}'_I(t'')|\chi_0\rangle }
where the perturbation is slowly switched on at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=-\infty} .
As mentioned before,we need to calculate the transition probability from
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\chi_0\rangle=|0;N_{k,\lambda},N_{k',\lambda'}=0\rangle} to the final state
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n;N_{k,\lambda}-1,N_{k',\lambda'}=1\rangle }
Therefore we need to calculate that following transition probability,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C(t)=\langle n;N_{k,\lambda}-1,N_{k',\lambda'}=1|\chi(t)\rangle }
Using second order time dependent perturbation theory the probability for such a transition is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C(t)=\frac{1}{i\hbar}\int_{-\infty}^{t}dt'\langle n;N_{k,\lambda}-1,N_{k',\lambda'}=1|\mathcal{H}'_I(t')|0;N_{k,\lambda},N_{k',\lambda'}=0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +\frac{1}{(i\hbar)^2}\int_{-\infty}^{t}dt'\int_{-\infty}^{t'}dt''\langle n;N_{k,\lambda}-1,N_{k',\lambda'}=1|\mathcal{H}'_I(t')\mathcal{H}'_I(t'')|0;N_{k,\lambda},N_{k',\lambda'}=0\rangle }
The required transition can be made by term proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A(r)}^2} )(the diamagnetic term)in first order, while term proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A(r)}} (paramagnetic term) gives non-zero overlap in second order perturbation theory. Therefore we have:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}C(t)&=\frac{1}{i\hbar}\int_{-\infty}^{t}dt'\langle n;N_{k,\lambda}-1,N_{k',\lambda'}=1| e^{\frac{i}{\hbar}\mathcal{H}^{(at)}_0t'}\left( \frac{e^2}{2mc^2}\mathbf{A(r},t')\cdot \mathbf{A(r},t')\right)e^{-\frac{i}{\hbar}\mathcal{H}^{(at)}_0t'} |0;N_{k,\lambda},N_{k',\lambda'}=0\rangle \\ &+ \frac{1}{(i\hbar)^2}\int_{-\infty}^{t}dt' \int_{-\infty}^{t'}dt''\langle n;N_{k,\lambda}-1,N_{k',\lambda'}=1|e^{\frac{i}{\hbar}\mathcal{H}^{(at)}_0t'}\left( -\frac{e}{mc}A(r,t')\cdot p\right)e^{-\frac{i}{\hbar}\mathcal{H}^{(at)}_0t'}\times\\ &\times e^{\frac{i}{\hbar}\mathcal{H}^{(at)}_0t''}\left( -\frac{e}{mc}A(r,t'')\cdot p\right)e^{-\frac{i}{\hbar}\mathcal{H}^{(at)}_0t''} |0;N_{k,\lambda},N_{k',\lambda'}=0\rangle\\ \end{align}}We can ignore the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf r-} dependence in gauge field by using dipole approximation, that is we can say Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{exp}(-iK.r)=1-iK.r }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}C(t)&=\frac{1}{i\hbar}\frac{e^2}{2mc^2}\int_{-\infty}^{t}dt'e^{\frac{i}{\hbar}(\epsilon_n-\epsilon_0)t'}\langle N_{k,\lambda}-1,N_{k',\lambda'}=1| A(t')\cdot A(t') |N_{k,\lambda},N_{k',\lambda'}=0\rangle\langle n|0\rangle\\ &+\frac{1}{(i\hbar)^2}\frac{e^2}{m^2c^2}\sum_{\alpha}\int_{-\infty}^{t}dt' \int_{-\infty}^{t'}dt''e^{\frac{i}{\hbar}(\epsilon_n-\epsilon_{\alpha})t'}e^{\frac{i}{\hbar}(\epsilon_{\alpha}-\epsilon_0)t''}\times\\ &\langle N_{k,\lambda}-1,N_{k',\lambda'}=1|A_{\mu}(t')A_{\nu}(t'')|N_{k,\lambda},N_{k',\lambda'}=0\rangle \langle n| p_{\mu} |\alpha\rangle \langle \alpha| p_{\nu} |0\rangle \\ \end{align}}
Let's define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{C(t)=C_1(t)+C_2(t)}}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}C_1(t) &=\frac{\delta_{n,0}}{i\hbar}\frac{e^2}{2mc^2} \frac{1}{V}\frac{2\pi\hbar c^2}{\sqrt{\omega_{k}\omega_{k'}}}\hat{\lambda}\cdot {\hat{\lambda}^{'*}} \langle N_{k,\lambda}-1,N_{k',\lambda'}=1|(a_{k\lambda}a^{\dagger}_{k'\lambda'}+a^{\dagger}_{k'\lambda'}a_{k\lambda}) |N_{k,\lambda},N_{k',\lambda'}=0\rangle \times\\ &\int_{-\infty}^{t}dt'e^{\frac{i}{\hbar}(\epsilon_n-\epsilon_0)t'}e^{-i(\omega_{k}-\omega_{k'})t'}e^{2\eta t'}\\ &=\frac{\delta_{n,0}}{i\hbar}\frac{e^2}{m} \frac{1}{V}\frac{2\pi\hbar }{\sqrt{\omega_{k}\omega_{k'}}}\hat{\lambda}\cdot {\hat{\lambda}^{'*}}\sqrt{N_{k\lambda}} \times\frac{e^{\frac{i}{\hbar}(\epsilon_n-\epsilon_0)t}e^{-i(\omega_{k}-\omega_{k'})t}e^{2\eta t}}{\frac{i}{\hbar}(\epsilon_n-\epsilon_0)-i(\omega_{k}-\omega_{k'})+2\eta} \end{align}}
The second order term is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} C_2(t)&= \frac{1}{(i\hbar)^2}\frac{e^2}{m^2c^2}\frac{1}{V}\frac{2\pi\hbar c^2}{\sqrt{\omega_{k}\omega_{k'}}}\sqrt{N_{k\lambda}} \sum_{\alpha}\int_{-\infty}^{t}dt' \int_{-\infty}^{t'}dt'' e^{\frac{i}{\hbar}(\epsilon_n-\epsilon_{\alpha})t'}e^{\frac{i}{\hbar}(\epsilon_{\alpha}-\epsilon_0)t''}\times\\ &\left( \langle n| p |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}^{'*}e^{-i\omega_{k}t'}e^{\eta t'}e^{i\omega_{k'}t''}e^{\eta t''}+ \langle n| p |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}e^{i\omega_{k'}t'}e^{\eta t'}e^{-i\omega_{k}t''}e^{\eta t''}\right)\\ &= \frac{1}{(i\hbar)^2}\frac{e^2}{m^2}\frac{1}{V}\frac{2\pi\hbar}{\sqrt{\omega_{k}\omega_{k'}}}\sqrt{N_{k\lambda}} \times\frac{e^{\frac{i}{\hbar}\left(\epsilon_n-\epsilon_0+\hbar\omega_{k'}-\hbar\omega_{k}\right)t}e^{2\eta t}}{\frac{i}{\hbar}\left(\epsilon_n-\epsilon_0+\hbar\omega_{k'}-\hbar\omega_{k}-2i\hbar\eta\right)} \times\\ &\sum_{\alpha}\left( \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}^{'*}}{\frac{i}{\hbar}\left(\epsilon_{\alpha}-\epsilon_0+\hbar\omega_{k'}-i\hbar\eta\right)}+ \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}}{\frac{i}{\hbar}\left(\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta\right)}\right)\\ \end{align}}
Therefore,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}C(t)&=C_1(t)+C_2(t)\\ &=-\frac{e^{\frac{i}{\hbar}\left(\epsilon_n-\epsilon_0+\hbar\omega_{k'}-\hbar\omega_{k}\right)t}e^{2\eta t}}{\left(\epsilon_n-\epsilon_0+\hbar\omega_{k'}-\hbar\omega_{k}-2i\hbar\eta\right)}\frac{\sqrt{N_{k\lambda}}}{V} \frac{2\pi \hbar e^2}{m\sqrt{\omega_{k}\omega_{k'}}}\times\\ &\left(\delta_{n,0}\hat{\lambda}\cdot{\hat{\lambda}}^{'*}-\frac{1}{m} \sum_{\alpha}\left( \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}^{'*}}{\epsilon_{\alpha}-\epsilon_0+\hbar\omega_{k'}-i\hbar\eta}+ \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}}{\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta}\right)\right)\\ \end{align}}
The time dependent probability is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}\mathcal{P}(t)&=|C(t)|^2\\ &=\frac{e^{4\eta t}}{\left(\epsilon_n-\epsilon_0+\hbar\omega_{k'}-\hbar\omega_{k}\right)^2+4\hbar^2\eta^2}\frac{N_{k\lambda}}{V^2} \frac{4\pi^2 \hbar^2 e^4}{m^2\omega_{k}\omega_{k'}}\times\\ &\left|\delta_{n,0}\hat{\lambda}\cdot{\hat{\lambda}}^{'*}-\frac{1}{m} \sum_{\alpha}\left( \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}^{'*}}{\epsilon_{\alpha}-\epsilon_0+\hbar\omega_{k'}-i\hbar\eta}+ \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}}{\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta}\right)\right|^2\\ \end{align}}
and the transition rate is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}\Gamma&=\frac{\partial \mathcal{P}(t)}{\partial t}\\ &=\frac{2\pi}{\hbar} \frac{N_{k\lambda}}{V^2} \frac{4\pi^2 \hbar^2 e^4}{m^2\omega_{k}\omega_{k'}}\times \delta\left(\epsilon_n-\epsilon_0-\hbar\omega_{k}+\hbar\omega_{k'}\right) \times\\ &\left|\delta_{n,0}\hat{\lambda}\cdot{\hat{\lambda}}^{'*}-\frac{1}{m} \sum_{\alpha}\left( \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}^{'*}}{\epsilon_{\alpha}-\epsilon_0+\hbar\omega_{k'}-i\hbar\eta}+ \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}}{\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta}\right)\right|^2\\ \end{align}}
We observe that, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{i}{\hbar}[\mathcal{H}_0^{(at)},r]=\frac{1}{m}p\;\;\Rightarrow\;\; \langle n| p |\alpha\rangle=\frac{i}{\hbar}m\langle n|[\mathcal{H}_0^{(at)},r] |\alpha\rangle=\frac{i}{\hbar}m(\epsilon_n-\epsilon_{\alpha})\langle n| r |\alpha\rangle }
Taking (as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta\rightarrow 0} ) we get,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}&\frac{1}{m} \sum_{\alpha}\left( \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}^{'*}}{\epsilon_{\alpha}-\epsilon_0+\hbar\omega_{k'}-i\hbar\eta}+ \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}}{\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta}\right)\\ &=\frac{i}{\hbar} \sum_{\alpha}\left( \frac{(\epsilon_n-\epsilon_{\alpha})\langle n| r |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}^{'*}}{\epsilon_{\alpha}-\epsilon_n+\hbar\omega_{k}-i\hbar\eta}+ \frac{(\epsilon_{\alpha}-\epsilon_0)\langle n| p |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| r |0\rangle\cdot{\hat{\lambda}}}{\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta}\right)\\ &=\frac{i}{\hbar} \sum_{\alpha}\left(-\langle n| r |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}^{'*}+ \langle n| p |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| r |0\rangle\cdot{\hat{\lambda}}\right)\\ &+i\omega_{k} \sum_{\alpha}\left( \frac{\langle n| r |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}^{'*}}{\epsilon_{\alpha}-\epsilon_n+\hbar\omega_{k}-i\hbar\eta}+ \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| r |0\rangle\cdot{\hat{\lambda}}}{\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta}\right)\\ &=\delta_{n0}\hat{\lambda}\cdot{\hat{\lambda}}^{'*}+i\omega_{k} \sum_{\alpha}\left( \frac{\langle n| r |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}^{'*}}{\epsilon_{\alpha}-\epsilon_n+\hbar\omega_{k}-i\hbar\eta}+ \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| r |0\rangle\cdot{\hat{\lambda}}}{\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta}\right)\\ \end{align}}
where in the second line we have used the energy conserving Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta-} function, giving Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_n+\hbar\omega_{k'}=\epsilon_0+\hbar\omega_{k}} . Using the above commutation relation again we finally find
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}&\frac{1}{m} \sum_{\alpha}\left( \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}^{'*}}{\epsilon_{\alpha}-\epsilon_0+\hbar\omega_{k'}-i\hbar\eta}+ \frac{\langle n| p |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| p |0\rangle\cdot{\hat{\lambda}}}{\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta}\right)\\ &=\delta_{n0}\hat{\lambda}\cdot{\hat{\lambda}}^{'*}+m\omega_{k}\omega_{k'} \sum_{\alpha}\left( \frac{\langle n| r |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| r |0\rangle\cdot{\hat{\lambda}}^{'*}}{\epsilon_{\alpha}-\epsilon_0+\hbar\omega_{k'}-i\hbar\eta}+ \frac{\langle n| r |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| r |0\rangle\cdot{\hat{\lambda}}}{\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta}\right)\\ \end{align}}
Therefore
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma =\frac{2\pi}{\hbar} \frac{N_{k\lambda}}{V^2} \frac{4\pi^2 \hbar^2 e^4}{m^2\omega_{k}\omega_{k'}}\times \delta\left(\epsilon_n-\epsilon_0-\hbar\omega_{k}+\hbar\omega_{k'}\right)m^2\omega^2_{k}\omega^2_{k'}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ( \sum_{\alpha}\left( \frac{\langle n|r|\alpha \rangle \hat{\lambda}\langle \alpha| r|0\rangle {\hat{\lambda}}^{'*}} {\epsilon_\alpha-\epsilon_0 + \hbar \omega_{k'}-i\hbar \eta} + \frac{\langle n| r |\alpha\rangle \hat{\lambda}^{'*}\langle \alpha| r|0\rangle \hat{\lambda}}{\epsilon_\alpha-\epsilon_0 - \hbar \omega_{k}-i\hbar \eta}\right)}
To get the total transition rate we need to sum over all wavevectors in a solid angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\Omega'} . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}dw\!\!&=\!\!\sum_{k'\in d\Omega'}\Gamma \\&= \frac{2\pi}{\hbar} \frac{d\Omega' \omega^2_{k'}}{8\pi^3c^3\hbar}\frac{N_{k\lambda}}{V} \frac{4\pi^2 \hbar^2 e^4}{m^2\omega_{k}\omega_{k'}}m^2\omega^2_{k}\omega^2_{k'}\left|\sum_{\alpha}\left( \frac{\langle n| r |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| r |0\rangle\cdot {\hat{\lambda}}^{'*}}{\epsilon_{\alpha}-\epsilon_0+\hbar\omega_{k'}-i\hbar\eta}+ \frac{\langle n| r |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| r |0\rangle\cdot {\hat{\lambda}}}{\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta}\right) \right|^2\\ &=d\Omega'\frac{e^4\omega_{k}\omega^3_{k'}}{c^3}\frac{N_{k\lambda}}{V} \left|\sum_{\alpha}\left( \frac{\langle n| r |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| r |0\rangle\cdot {\hat{\lambda}}^{'*}}{\epsilon_{\alpha}-\epsilon_0+\hbar\omega_{k'}-i\hbar\eta}+ \frac{\langle n| r |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| r |0\rangle\cdot {\hat{\lambda}}}{\epsilon_{\alpha}-\epsilon_0-\hbar\omega_{k}-i\hbar\eta}\right) \right|^2\\\end{align}}where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_n+\hbar\omega_{k'}=\epsilon_0+\hbar\omega_{k}} . Finally the differential cross-section is found by dividing by the photon flux Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{c N_{k\lambda}/V}} to yield
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega'} =\frac{e^4\omega_{k}\omega^3_{k'}}{c^4} \left|\sum_{\alpha}\left( \frac{\langle n| r |\alpha\rangle \cdot \hat{\lambda}\langle \alpha| r |0\rangle\cdot{\hat{\lambda}}^{'*}}{\epsilon_{0}-\epsilon_{\alpha}-\hbar\omega_{k'}+i\hbar\eta}+ \frac{\langle n| r |\alpha\rangle \cdot \hat{\lambda}^{'*}\langle \alpha| r |0\rangle\cdot{\hat{\lambda}}}{\epsilon_{0}-\epsilon_{\alpha}+\hbar\omega_{k}+i\hbar\eta}\right) \right|^2}
Therefore the scattering cross-section is inversely proportional to the fourth power of wavelength ( for elastic scattering). This explains why sky is blue since blue light having lower wavelength, gets scattered more.Non-perturbative methods
Apart from the conventional perturbative methods, there also exist non-perturbative methods to approximately determine the lowest energy eigenstate or ground state, and some excited states, of a given system. Superconductivity and the fractional quantum Hall effect are examples of problems that were solved using non-perturbative methods. One of the important methods in the approximate determination of the wave function and eigenvalues of a system is the Variational Method, which is based on the variational principle. The variational method is a very general one that can be used whenever the equations can be put into the variational form. The variational method is now a pringboard to many numerical computations.
Principle of the Variational Method
Consider a completely arbitrary system with time independent Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} and we assume that it's entire spectrum is discrete and non-degenerate.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}|{\varphi}_{n}\rangle} =Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}_{n}|{\varphi}_{n}\rangle} ; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = 0,1,2,\dots \!}
Let's apply the variational principle to find the ground state of the system.Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |{\psi}\rangle } be an arbitrary ket of the system. We can define the expectation value of the Hamiltonian as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle=\frac{\langle{\psi}|\mathcal{H}|{\psi}\rangle}{\langle{\psi}|{\psi}\rangle}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (4.1.1) }
Of course, if the wavefunction is normalized so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi}|{\psi}\rangle=1 } , then the expectation value of the hamiltonian is just: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle=\langle{\psi}|\mathcal{H}|{\psi}\rangle }
The variational principle states that,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle\geq \mathcal{E}_0 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (4.1.2)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle= \mathcal{E}_0 \qquad \qquad \qquad \qquad \qquad \qquad} is only true if the wave functions used in the expectation value are the exact wave functions of the true ground state for the Hamiltonian; they can not be unperturbed or approximate wave functions.
Because the expectation value of the Hamiltionian is always greater than or equal to the ground state energy, this gives an upper bound for the ground state energy when using unperturbed wavefunctions to calculate the expectation value.
If you are making a guess at the wavefunction, but do not know it explicitly, you can write it up to a parameter and then minimize the expectation value of the hamiltonian with respect to that parameter. For example, we can write the ground state wavefunction of the hydrogen atom, up to a parameter as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi= \dfrac{e^{-b r}}{\sqrt{\pi a_o^3}}}
You would then minimize the expectation value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} \!} with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b \! } , lowering your upper bound as far as possible so that you have a better idea of the true value of the energy.
In some cases a lower bound can also be found by a similar method. In the case that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi}|V|{\psi}\rangle\geq \ 0 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V \!} is said to be a positive operator because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi}|\mathcal{H}+V|{\psi}\rangle = E \geq \langle{\psi}|V|{\psi}\rangle} . Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi}|V|{\psi}\rangle} is a lower bound for the energy.
Since the exact eigenfunctions of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |{\varphi}\rangle } form a complete set, we can express our arbitrary ket Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |{\psi}\rangle } as a linear combination of the exact wavefunction.Therefore,we haveFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |{\psi}\rangle=\sum_{n} C_n |{\varphi}_n\rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (4.1.3)}
Multiplying both sides by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi}|\mathcal{H}} we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi}|\mathcal{H}|{\psi}\rangle= \sum_{n} |C_n|^{2}\langle{\varphi}_n| \mathcal{H} |{\varphi}_n\rangle =\sum_{n}|C_n|^{2} \mathcal{E}_n }
However, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}_n \geq \mathcal{E}_0 } . So, we can write the above equation asFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi}|\mathcal{H}|{\psi}\rangle \geq \mathcal{E}_0 \sum_{n} |C_n|^{2}}
Or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}_0 \leq \frac{ \langle{\psi}|\mathcal{H}|{\psi}\rangle } {\langle{\psi}|{\psi}\rangle} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (4.1.4)}
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\langle{\psi}|{\psi}\rangle}=\sum_{n} |C_n|^{2}} , thus proving eq. #4.1.2.
Thus eq. #4.1.2 gives an upper bound to the exact ground state energy. For the equality to be applicable in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad \text{(4.1.2)}} all coefficients except Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}_0} should be zero and then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |{\psi}\rangle } will be the eigenvector of the Hamiltonian and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}_0} the ground state eigenvalue.Generalization of Variational Principle: The Ritz Theorem.
We claim that the expectation value of the Hamiltonian is stationary in the neighborhood of its discrete eigenvalues. Let us again consider the expectation value of the Hamiltonian eq.#4.1.1.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle=\frac{\langle{\psi}|\mathcal{H}|{\psi}\rangle}{\langle{\psi}|{\psi}\rangle}}
Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle} is considered as a functional of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi\rangle} . Let us define the variation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi\rangle} goes to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi\rangle +| \delta \psi\rangle } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle | \delta \psi\rangle } is considered to be infinetly small. Let us rewrite eq.#4.1.1 as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle\langle{\psi}|{\psi}\rangle=\langle{\psi}|\mathcal{H}|{\psi}\rangle\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (4.2.1)} .
Differentiating the above relation, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi}|{\psi}\rangle\delta\langle\mathcal{H}\rangle+\langle\mathcal{H}\rangle[\langle{\psi}|\delta{\psi}\rangle+\langle\delta{\psi}|{\psi}\rangle]=\langle{\psi}|\mathcal{H}|{\delta\psi}\rangle+\langle{\delta\psi}|\mathcal{H}|{\psi}\rangle\qquad \qquad \qquad \qquad \qquad (4.2.2)}
However, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle} is just a c-number, so we can rewrite eq #4.2.2 asFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi} | {\psi}\rangle\delta\langle\mathcal{H}\rangle =\langle{\psi} | [\mathcal{H}-\langle\mathcal{H}\rangle] | {\delta\psi}\rangle+\langle{\delta\psi} | [\mathcal{H}-\langle\mathcal{H}\rangle]|{\psi}\rangle\qquad \qquad \qquad \qquad \qquad (4.2.3)} .
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \langle \mathcal{H}\rangle=0 } , then the mean value of the Hamiltonian is stationary.Therefore,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi} | [\mathcal{H}-\langle\mathcal{H}\rangle] | {\delta\psi}\rangle+\langle{\delta\psi} | [\mathcal{H}-\langle\mathcal{H}\rangle]|{\psi}\rangle=0 } .
Define, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |{\varphi}\rangle =|[\mathcal{H}-\langle\mathcal{H}\rangle] | {\psi}\rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (4.2.4)} .Hence,eq. #4.2.3 becomes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\varphi}|\delta{\psi}\rangle+ \langle\delta{\psi}|{\varphi}\rangle=0 \qquad \qquad \qquad \qquad \qquad \qquad (4.2.5)} .
We can define the variation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |{\psi}\rangle} asFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\delta{\psi}\rangle=\delta\lambda|\delta{\psi}\rangle} ,
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda \!} being a small (real) number. Therefore eq #4.2.5 can be written asFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi}|{\psi}\rangle \delta\lambda=0 \qquad \qquad \qquad \qquad \qquad \qquad (4.2.6)}
Since the norm is zero, the wave function itself should be zero. Keeping this in mind, if we analyze eq #4.2.4, it's clear that we can rewrite it as an eigenvalue problem.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}|{\psi}\rangle=\langle\mathcal{H}\rangle|{\psi}\rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (4.2.7)} .
Finally, we can say that expectation value of the Hamiltonian is stationary if the arbitrary wavefunction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |{\psi}\rangle} is actually the eigenvector of the Hamiltonian with the stationary values of the expectation values of the Hamiltonian, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle } being precisely the eigen values of the Hamiltonian.The general method is to find an approximate trial wavefunction that contain one or more parameters Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha, \beta, \gamma, \dots \! } . If the expectation value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle } can be differentiated with respect to these parameters, the extrema of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle } can be found using the following equation.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial\langle\mathcal{H}\rangle}{\partial\alpha}=\frac{\partial\langle\mathcal{H}\rangle}{\partial\beta}=\frac{\partial\langle\mathcal{H}\rangle}{\partial\gamma}= \dots = 0 }
The absolute minimum of the expectation value of the Hamiltonian obtained by this method correspond to the upper bound on the ground state energy. The other relative, extrema corresponds to excited states. There are many virtues of using the Variational method. Even a poor approximation to the actual wave function can yield an excellent approximation to the actual energy.
Upper Bound on First Excited State
We claim that if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle{\psi}|{\varphi}_0\rangle=0} , then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle \geq \mathcal{E}_1} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}_1} is the energy of the first excited state and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |{\varphi}_0\rangle} is the exact ground state of the Hamiltonian.
From Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad\text{(4.3)}} it is clear that if the above condition is satisfied then, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{C}_0=0 } . Therefore,we can write the expectation value of the hamiltonian as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle =\sum_{n=1} |\mathcal{C}_n|^2\mathcal{E}_n \geq \mathcal{E}_1 \sum_{n=1} |\mathcal{C}_n|^2}
Thus if we can find a suitable trial wavefunction that is orthogonal to the exact ground state wavefunction, then by calculating the expectation value of the Hamiltonian, we get an upperbound on the first excited state. The trouble is that we might not know the exact ground state( which is one reason why we implement the variational principle). However if we have a Hamiltonian which is an even function, then the exact ground state will be an even function and hence any odd trial function will be a right candidate as the first excited state wavefunction.
Trial wavefunction with linear parameter and the Hylleraas- Undheim Theory
Let us consider a set of orthonormal wavefunctions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \{ \psi \right \}} . So any arbitrary trial wavefunction may be constituted by the linear combination of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \{ \psi \right \}} . That is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi = \sum_{n} a_n \psi _{n} }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n} are linear parameters. The energy expectation value is now defined as,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\phi} = \left \langle H \right \rangle= \frac{(\phi,H\phi)}{(\phi,\phi)}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\phi} = \frac{\sum_{n}\sum_{n{}'} a_n a_n{}' (\psi _{n}, H \psi _{n}) }{\sum_{n}\sum_{n{}'} a_n a_n{}' (\psi _{n}, \psi _{n}) }} ...............................(A)
Since we have not told about the symmetry or orthonormality of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \{ \psi \right \}} , lets us consider,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_nn^{'}= (\psi _{n}, H \psi _{n})} and
Now if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \{ \psi \right \}} are orthonormal then, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_{nn^'}= \delta_{nn^'}}
Therefore equation (A) stands as,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\phi}= \frac{\sum_{n}\sum_{n{}'} a_n a_n{}' H_{nn^{'} }}{\sum_{n}\sum_{n{}'} a_n a_n{}' \Delta_{nn^{'}}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\phi}\sum_{n}\sum_{n{}'} a_n a_n{}' \Delta_{nn^{'}} - \sum_{n}\sum_{n{}'} a_n a_n{}' H_{nn^{'} } } = 0
Now minimizing the above equation with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_n{}'} , we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n} a_n E_{\phi} \Delta_{nn^{'}} - \sum_{n} a_n H_{nn^{'}} } = 0omiting the subscript Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} we can write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n} a_n ( H_{nn^{'}} - E \Delta_{nn^{'}}) } = 0
For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{'}} = 1,2,3,...... we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_1 ( H_{11} - E \Delta_{11} + a_2 ( H_{12} - E \Delta_{12}+ ...............a_N ( H_{1N} - E \Delta_{1N}) } = 0
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_1 ( H_{21} - E \Delta_{21} + a_2 ( H_{22} - E \Delta_{22}+ ...............a_N ( H_{2N} - E \Delta_{2N}) } = 0 . .
.
.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_1 ( H_{N1} - E \Delta_{N1} + a_2 ( H_{N2} - E \Delta_{N2}+ ...............+ a_N ( H_{2N} - E \Delta_{NN}) } = 0
Now in Matrix form, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} H_{11} - E \Delta_{11} & H_{12} - E \Delta_{12} & ........ & H_{1N} - E \Delta_{1N}\\ .& .& .&. \\ .& .& .&. \\ H_{N1} - E \Delta_{N1} & H_{N2} - E \Delta_{N2} & ........ & H_{NN} - E \Delta_{NN} \end{pmatrix} \begin{pmatrix} a_{1}\\ .\\ .\\ a_{n} \end{pmatrix} = 0}For the non-trivial values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n}} we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{vmatrix} H_{11} - E \Delta_{11} & H_{12} - E \Delta_{12} & ........ & H_{1N} - E \Delta_{1N}\\ .& .& .&. \\ .& .& .&. \\ H_{N1} - E \Delta_{N1} & H_{N2} - E \Delta_{N2} & ........ & H_{NN} - E \Delta_{NN}\end{vmatrix} }
The solution of this NxN determinant will give N roots say Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}^{N},E_{1}^{N}.......E_{N-1}^{N}} . From the values the first one Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}^{N}} will give the upper bound to the ground state energy.Now substituting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}^{N}} in 1st equation of the set of linear equations and then solving them we get the values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n}} and then the wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} . Now if we add one more wave function in then the secular equation will give (N+1) values E, say Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}^{N+1},E_{1}^{N+1},E_{2}^{N+1}...........}
The previous energy level Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}^{N},E_{1}^{N}...........} will now spirit to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{0}^{N+1},E_{1}^{N+1}...........}
This theorem is known as the Hylleraas- Undheim Theorem.
A Special Case where The Trial Functions form a Subspace
Assume that we choose for the trial kets the set of kets belonging to a vector subspace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{F}} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}} . In this case, the variational method reduces to the resolution of the eigenvalue equation of the Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} inside Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{F}} , and no longer in all of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}} .
To see this, we simply apply the argument of Sec. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{4.2}} , limiting it to the kets Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi\rangle} of the subspace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{F}} . The maxima and minima of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle} , characterized by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \langle\mathcal{H}\rangle=0} , are obtained when is an eigen vector of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{F}} . The corresponding eigenvalues constitute the variational method approximation for the true eigenvalues of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}} .
We stress the fact that the restriction of the eigenvalue equation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} to a subspace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{F}} of the state space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}} can considerably simplify its solution. However, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{F}} is badly chosen, it can also yield results which are rather far from true eigenvalues and eigenvectors of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{E}} . The subspace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{F}} must therefore be chosen so as to simplify the problem enough to make it soluble, without too greatly altering the physical reality. In certain cases, it is possible to reduce the study of a complex system to that of a two-level system, or at least, to that of a system of a limited number of levels. Another important example of this procedure is the method of the linear combination of atomic orbitals, widely used in molecular physics. This method essentially consists of the determination of the wave functions of electrons in a molecule in the form of linear combination of the eigenfunctions associated with the various atoms which constitute the molecule, treated as if they were isolated. It, therefore, limits the search for the molecular states to a subspace chosen using physical criteria. Similarly, in complement, we shall choose as a trial wave function for an electron in a solid a linear combination of atomic orbitals relative to the various ions which constitute this solid.
Applications of Variational Method
Harmonic Potential
Armed with the variational method let us apply it first to a simple Hamiltonian. Consider the following Hamiltonian with harmonic potential whose eigenvalues and eigenfunctions are known exactly. We will determine how close we can get with a suitable trial function.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+\frac{1}{2}mw^2x^2 \qquad \qquad\ \qquad \qquad \qquad \qquad (4.5.1.1)}
The above hamiltonian is even therefore, to find the ground state upper bound we need to use an even trial function. Let us consider the following state vector with one parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{\alpha}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)=A e^{-\alpha x^2}\qquad;\qquad\alpha>0 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (4.5.1.2)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A \,\!} is the normalization constant.Let us normalize the trial wavefunction to be unity
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1=\langle\psi|\psi\rangle= |A|^2\int_{-\infty}^{\infty}e^{-2\alpha x^2} dx =|A|^2\sqrt{\frac{\pi}{2\alpha}} \Rightarrow A=\left[ \frac{2\alpha}{\pi}\right] ^{1/4}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad(4.5.1.3)}
While, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle= |A|^2 \int_{-\infty}^{\infty} dx e^{-\alpha x^2}\left[ -\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+\frac{1}{2}mw^2x^2 \right] e^{-\alpha x^2}=\frac{\hbar^2\alpha}{2m}+\frac{mw^2}{8\alpha}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad(4.5.1.4)}Minimizing the expectation value with respect to the parameter we get,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial\langle\mathcal{H}\rangle}{\partial\alpha}= \frac{\hbar^2}{2m}-\frac{mw^2}{8\alpha^2}=0 \Rightarrow \alpha=\frac{mw}{2\hbar}}
Putting this value back in the expectation value, we getFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \mathcal{H}\rangle_{min}=\frac{1}{2}\hbar w}
Due to our judicious selection of trial wavefunction, we were able to find the exact ground state energy. If we want to find the first excited state, a suitable candidate for trial wavefunction would be an odd function.
Rational wave functionsThe calculations of the previous sections enabled us to familiarize ourselves with the variational method, but they do not really allow us to judge its effectiveness as a method of approximation, since the families chosen always included the exact wave function. Therefore, we shall now choose trial functions of a totally different type, for example
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{a}(x)=\frac{1}{x^2+a}\qquad; \quad a>0 }
A simple calculation then yields:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \psi_{a}|\psi_{a}\rangle=\int_{-\infty}^{+\infty}\frac{dx}{\left(x^2+a\right)^2}=\frac{\pi}{2a\sqrt{a}}}
and finally:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle (a)=\frac{\hbar^2}{4m}\frac{1}{a}+\frac{1}{2}m \omega^2 a}
The minimum value of this function is obtained for:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=a_{0}=\frac{1}{\sqrt{2}}\frac{\hbar}{m \omega}}
and is equal to:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle (a_{0})=\frac{1}{\sqrt{2}}\, \hbar \omega }
The minimum value is therefore equal to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{2}} times the exact ground state energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega/2} . To measure the error committed, we can calculate the ratio of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle (a_{0})-\hbar \omega/2} to the energy quantum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\langle\mathcal{H}\rangle (a_{0})-\frac{1}{2} \hbar \omega}{\hbar \omega}=\frac{\sqrt{2}-1}{2} \simeq 20 \%}
DiscussionsThe example of the previous section shows that it is easy to obtain the ground state energy of a system, without significant error, starting with arbitrary chosen trial kets. This is one of the principal advantages of the variational method. Since the exact eigenvalue is a minimum of the mean value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle } , it is not surprising that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathcal{H}\rangle } does not vary much near this minimum.
On the other hand, as the same reasoning shows, the "approximate" state can be rather different from the true eigenstate. Thus, in the example of the previous section, the wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\left(x^2+a_{0}\right)}} decreases too rapidly for small values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \!} and much too slowly when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \!} becomes large. The table below gives quantitative support for this qualitative assertion. It gives, for various values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2 \!} , the values of the exact normalized eigenfunction:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi_{0}(x)=\left(\frac{2 \alpha_{0}}{\pi}\right)^{1/4} e^{-\alpha_{0} x^2}}
and of the approximate normalized eigenfunction of the wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\left(x^2+a_{0}\right)}} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\frac{2}{\pi}} (a_{0})^{3/4} \psi_{a_{0}}(x) = \sqrt{\frac{2}{\pi}} \frac{(a_{0})^{3/4}}{x^2+a_{0}} = \sqrt{\frac{2}{\pi}} \left(2 \sqrt{2} \alpha_{0} \right)^{1/4} \frac{1}{1+2\sqrt{2} \alpha_{0} x^2}} ,
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_0 = \frac{1}{2\sqrt2 \alpha_0} } .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\sqrt{\alpha_{0}}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{2\alpha_0}{\pi}\right)^{1/4}e^{-\alpha_0 x^2}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\frac{2}{\pi}} \frac{\left(2 \sqrt{2} \alpha_0 \right)^{1/4}}{1+2\sqrt{2} \alpha_{0} x^2}} 0 0.893 1.034 1/2 0.696 0.606 1 0.329 0.270 3/2 0.094 0.141 2 0.016 0.084 5/2 0.002 0.055 3 0.0001 0.039 Therefore, it is necessary to be very careful when physical properties other than the energy of the system are calculated using the approximate state obtained from the variational method. The validity of the result obtained varies enormously depending on the physical quantity under consideration. In the particular problem which we are studying here, we find, for example, that the approximate mean value of the operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^2 \!} is not very different from the exact value:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\langle \psi_{a_{0}}|X^2|\psi_{a_{0}}\rangle}{\langle \psi_{a_{0}}|\psi_{a_{0}}\rangle}=\frac{1}{\sqrt{2}}\frac{\hbar}{m \omega}}
which is to be compared with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar/{2 m \omega}} . On the other hand, the mean value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X^4} is infinite for the approximate normalized eigenfunction, while it is, of course, finite for the real wave function. More generally, the table shows that the approximation will be very poor for all properties which depend strongly on the behavior of the wave function for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \gtrsim 2/\sqrt{\alpha_{0}}} .
The drawback we have just mentioned is all the more serious as it is very difficult, if not impossible, to evaluate the error in a variational calculation if we do not know the exact solution of the problem (and, of course, if we use the variational method, it is because we do not know this exact solution).
The variational method is therefore a very flexible approximation method, which can be adapted to very diverse situations and which gives great scope to physical intuition in the choice of trial kets. It gives good values for the energy rather easily, but the approximate state vectors may present certain completely unpredictable erroneous features, and we can not check these errors. This method is particularly valuable when physical arguments give us an idea of the qualitative or semi-qualitative form of the solutions.
Here is another problem related to the energy of the ground state and first excited state of a harmonic potential. -problem1Delta Function Potential
As another example lets consider the delta function potential.
Suppose Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = \frac{-\hbar^2}{2m}\frac{d^2}{dx^2} - \alpha \delta(x) } . Use as a trial wave function, a gaussian function. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x) = Ae^{-bx^2} }
First normalizing this:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1=|A|^2 \int_{-\infty}^{\infty} e^{-2bx^2}dx = |A|^2 \sqrt(\frac{\pi}{2b}) \rightarrow A=(\frac{2b}{\pi})^{1/4} }
First calculate <T> then <V>.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <T>= -\frac{\hbar^2}{2m}|A|^2\int_{-\infty}^{\infty} e^{-bx^2}\frac{d^2}{dx^2}(e^{-bx^2})dx = \frac{\hbar^2b}{2m} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <V>=-\alpha^2|A|^2\int_{-\infty}^{\infty} e^{-bx^2}\delta(x)dx = -\alpha\sqrt(\frac{2b}{\pi})}
Evidently Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <H> = \frac{\hbar^2b}{2m}-\alpha\sqrt(\frac{2b}{\pi}) }
Minimizing with respect to the parameter b:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d}{db}<H> = \frac{\hbar^2}{2m}-\frac{\alpha}{\sqrt(2\pi b)} = 0 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b = \frac{2m^2 \alpha^2}{\pi \hbar^4} }
So, plugging b back into the expression for the expectation value, we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <H>_{min}=-\frac{m \alpha^2}{\pi \hbar^2} }
Ground State of Helium atom
Let us use variational principle to determine the ground state energy of a Helium atom with a stationary nucleus. Helium atom has two electrons and two protons. For simplicity, we ignore the presence of neutrons. We also assume that the atom is non relativistic and ignore spin.
The Hamiltonian can be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = -\frac{\hbar^2}{2m}\left(\boldsymbol\nabla_1^2+\boldsymbol \nabla_2^2\right)- \frac{Ze^2}{|\vec{r}_1|} - \frac{Ze^2}{|\vec{r}_2|}+\frac{e^2}{|\vec{r}_1-\vec{r}_2|}, \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \mbox{(4.5.3.1)}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}_1,\vec{r}_2 \!} are the coordinates of the two electrons.
If we ignore the mutual interaction term, then the wavefunction will be the product of the two individual electron wavefunction which in this case is that of a hydrogen like atom. Therefore, the ground state wavefunction can be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_0(\vec{r}_1,\vec{r}_2)=\psi_{100}( \vec{r}_1)\psi_{100}(\vec{r}_2),\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \mbox{(4.5.3.2)}}
where we ignored spin and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{100}\left(\vec{r}_{1,2}\right)=\left(\frac{Z^3}{\pi{a_0}^3}\right)^{1/2} \exp\left[-{\frac{Z |\vec{r}_{1,2}|}{a_0}}\right], \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \mbox{(4.5.3.3)}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_0 = \frac{\hbar^2}{me^2}. \! }
Therefore we can write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{0}\left(\vec{r}_1,\vec{r}_2\right)=\frac{Z^3}{\pi{a_0}^3} \exp\left[-{\frac{Z ( |\vec{r}_1|+|\vec{r}_2|)}{a_0}}\right]. \qquad \qquad\qquad \qquad \qquad \qquad \qquad \qquad \qquad \mbox{(4.5.3.4)}}
We can write the lowest unperturbed energy for this situation with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=2\!} asFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0' = 2 \left( -\frac{m(Ze^2)^2}{2\hbar^2}\right) \simeq 2\left(-Z^2 \times 13.6 eV \right) = - 4 \times 13.6 eV = -108.8 eV. \qquad \qquad \mbox{(4.5.3.5)} }
The first order correction to the energy is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta E = \left\langle V \left( \vec{r}_1, \vec{r}_2 \right) \right\rangle = \int \int \left| \psi_0\left(\vec{r}_1, \vec{r}_2 \right) \right|^2 \frac{Ze^2}{\left| \vec{r}_1 - \vec{r}_2 \right|} d^3 r_1 d^3 r_2 = \frac{5Ze^2}{4a_0} = \frac{5}{2} \times 13.6eV = 34 eV. }
Therefore, the ground state energy in first approximation is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0 = E_0' + \Delta E = - 108.8 eV + 34 eV = - 74.8 eV \!}
However, the ground state energy has been experimentally determined accurately to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -78.86 eV \!} . Therefore, our model is not a good one. Now, let us apply variational method using a trial wavefunction. The trial wavefucntion we are going to use is #4.5.3.2 itself but we will allow Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z \!} to remain a free parameter. This argument is perfectly valid since each electron screens the nuclear charges seen by the other electron and hence the effective atomic number is less than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \!} .
We can manipulate the Hamiltonian with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z \!} going to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma \! } and rewriting the potential term as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\sigma e^2}{|\vec{r}|}+\frac{(Z-\sigma) e^2}{|\vec{r}|}} . So the Hamiltonian becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}= -\frac{\hbar^2}{2m}(\boldsymbol\nabla_1^2+\boldsymbol \nabla_2^2)- \frac{\sigma e^2}{|\vec{r}_1|}-\frac{(Z-\sigma) e^2}{|\vec{r}_1|}-\frac{\sigma e^2}{|\vec{r}_2|}-\frac{(Z-\sigma) e^2}{|\vec{r}_2|}+\frac{e^2}{|\vec{r}_1-\vec{r}_2|} }
Now we can use the variational principle. The expectation value of the Hamiltonian is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle \mathcal{H}\rangle = & \int{d^3r_1}\int{d^3r_2} \psi^*_{100}(\vec{r}_1)\psi^*_{100}(\vec{r}_2) \\ & \times \left[-\frac{\hbar^2}{2m}\boldsymbol\nabla_1^2-\frac{(Z-\sigma) e^2}{|\vec{r}_1|}- \frac{\sigma e^2}{|\vec{r}_1|} -\frac{\hbar^2}{2m}\boldsymbol\nabla_2^2-\frac{(Z-\sigma) e^2}{|\vec{r}_2|}-\frac{\sigma e^2}{|\vec{r}_2|}+\frac{e^2}{|\vec{r}_1-\vec{r}_2|}\right] \psi_{100}( \vec{r}_1)\psi_{100}(\vec{r}_2)\qquad \mbox{(4.5.3.6)} \end{align} }The first two terms give
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0^{(1)}(\sigma)=- \frac{(Z-\sigma)^2 me^4}{2\hbar^2}.}
The fourth and fifth term will give the same. The third term and sixth term will give
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0^{(2)}(\sigma)=-{\sigma e^2} \left\langle\frac{1}{r_1}\right\rangle = -{\sigma e^2}\frac{\left(Z-\sigma\right)}{a_0} = - \frac{me^4}{\hbar^2} \sigma \left(Z-\sigma\right).}
The seventh term will give an expectation value of
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0^{(3)}(\sigma)= \frac{5 \left(Z-\sigma\right) m e^4}{8\hbar^2}. }
Adding all this we get,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} E_0(\sigma) &= -\frac{m e^4}{\hbar^2}\left( \left(Z - \sigma\right)^2 + 2 \sigma\left(Z-\sigma\right) - \frac{5 \left(Z - \sigma\right)}{8}\right) \\ & = -\frac{e^2}{a_0}\left( Z^2 - \frac{5}{8}Z + \frac{5}{8}\sigma - \sigma^2 \right), \end{align} \qquad \qquad \qquad \qquad \qquad \mbox{(4.5.3.7)} }where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_0 = \frac{\hbar^2}{me^2}. \!}
Excercise 18.22 of E. Merzbacher's Quantum Mechanics (3rd Ed.)
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma \! } in #4.5.3.7 is the variational parameter, we can minimize the energy, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0(\sigma) \!} with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma \! } . That is,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial E_0(\sigma)}{\partial \sigma} = -\frac{e^2}{a_0} \left( \frac{5}{8} - 2 \sigma \right) = 0. }
This will give us
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \frac{5}{16}.}
Therefore, putting this value in #4.5.3.7 , then we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0\left(\frac{5}{16}\right) = - \left(Z-\frac{5}{16}\right)^2 \frac{e^2}{a_0} = - \frac{Z_{\mbox{eff}}^2 e^2}{a_0}, }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{\mbox{eff}} = \left( Z - \sigma \right) = \left( Z - \frac{5}{16} \right). }
Putting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=2 \!} , we get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{\mbox{eff}} = 1.6875. \!} Substituting this, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{\mbox{eff}} \! } in #4.5.3.5 instead of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z \! } , we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0 = -77.46 eV \!}
which is very close to the experimental valueFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( \sim - 78.86 eV \right) \! } . Thus, using variational principle we were able to calculate the ground state energy of the helium atom very close to the experimental value.
A sample problem related Rayleigh_Ritz variational principle: Exercise 18.23 of Quantum Mechanics, 3rd Ed., which is written by Eugen Merzbacher: [1]
A problem related to the variational principle and non-degenerate perturbation theory: problem
Spin
General Theory of Angular Momentum
Up to now we have been working with the rotational degree of freedom using the orbital angular momentum. Namely we use the operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf L} (the generator of rotations in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^{3}} ) to construct wave functions which carry the rotational information of the system.
To clarify, all that we have done consists of quantizing everything that we know from classical mechanics. Specifically:
- Invariance of time translation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow } Conservation of the Hamiltonian
- Invariance of Spatial translation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow } Conservation of the Momentum
- Invariance of Spacial Rotations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow } Conservation of Orbital Angular Momentum
However nature shows that there are other kinds of degrees of freedom that don't have classical analog. The first one was observed for the first time in 1922 by Stern and Gerlach (see Cohen-Tannoudji Chap 4). They saw that electrons have one additional degree of freedom of the angular momentum. This degree of freedom was called "Spin 1/2" since they exhibit just two single results: Up and Down. It is interesting to note that from the algebra of angular momenta, it is necessary that spins take on either half-integer or integer values; there is no continuous range of possible spins. (For example, one will never find a spin 2/3 particle.)
Spin 1/2 is the first truly revolutionary discovery of quantum mechanics. The properties of this physical quantity in itself, the importance of its existence, and the universality of its physical effects were totally unexpected. The physical phenomenon is the following. In order to describe completely the physics of an electron, one cannot use only its degrees of freedom corre- sponding to translations in space. One must take into account the existence of an internal degree of freedom that corresponds to an intrinsic angular mo- mentum. In other words, the electron, which is a pointlike particle, “spins” on itself. We use quotation marks for the word “spins”. One must be cautious with words, because this intrinsic angular momentum is purely a quantum phenomenon. It has no classical analogue, except that it is an angular mo- mentum. One can use analogies and imagine that the electron is a sort of quantum top. But we must keep in mind the word “quantum”. The electron is a pointlike object down to distances of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-18}} m.One must admit that a pointlike object can possess an intrinsic angular momentum.
The goal of this section is to extend the notion of orbital angular momentum to a general case. For this we use the letter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{J}} for this abstract angular momentum. As we will see, orbital angular momentum is just a simple case of the general angular momentum.
Experimental results
Experimentally, this intrinsic angular momentum, called spin, has the follow- ing manifestations (we do not enter in any technical detail):
1. If we measure the projection of the spin along any axis, whatever the state of the electron, we find either of two possibilities:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar}{2}} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\hbar}{2}}
There are two and only two possible results for this measurement.
2.Consequently, if one measures the square of any component of the spin, the result is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar}{4}} with probability one.
3. Therefore, a measurement of the square of the spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{2}=S_{x}^{2}+S_{y}^{2}+S_{z}^{2}} gives the result
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{2}=\frac{3\hbar^{2}}{4}}
4. A system that has a classical analogue, such as a rotating molecule, can rotate more or less rapidly on itself. Its intrinsic angular momentum can take various values. However, for the electron, as well as for many other particles, it is an amazing fact that the square of its spin S2 is always the same. It is fixed: all electrons in the universe have the same values of the square of their spins Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{2}=\frac{3\hbar^{2}}{4}} . The electron “spins” on itself, but it is not possible to make it spin faster.
One can imagine that people did not come to that conclusion immediately. The discovery of the spin 1/2 of the electron is perhaps the most breathtaking story of quantum mechanics.
The elaboration of the concept of spin was certainly the most difficult step of all quantum theory during the first quarter of the 20th century. It is a real suspense that could be called the various appearances of the number 2 in physics. There are many numbers in physics; it is difficult to find a simpler one than that.
And that number 2 appeared in a variety of phenomena and enigmas that seemed to have nothing to do a priori with one another, or to have a common explanation. The explanation was simple, but it was revolutionary. For the first time people were facing a purely quantum effect, with no classical analogue. Nearly all the physical world depends on this quantity, the spin 1/2.
The challenge existed for a quarter of a century (since 1897). Perhaps, there was never such a long collective effort to understand a physical structure. It is almost impossible to say who discovered spin 1/2, even though one personality dominates, Pauli, who put all his energy into finding the solution.
We show that in order to manipulate spin 1/2, and understand technical- ities we essentially know everything already. We have done it more or less on two-state systems.
Note on Hund's RulesHund's Rules describe Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L-S \!} coupling approximation as long as there is convergence for an atom with a given configuration. Below list the steps.
1. Choose a maximum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S \!} (total spin) consistent with Pauli exclusion principle
2. Choose a maximum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L \!} (angular momentum)
3. If the shell is less than half full, choose Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J=J_{min} =|L-S| \!}
4. If the shell is more than half full, choose Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J=J_{max} =L+S \!}
For example, we use Silicon: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1s^2 2s^2 2p^6 3s^2 3p^2 \!} then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S= \dfrac{1}{2} + \dfrac{1}{2} = S_{max} \!} for 2 spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{1}{2}\!} particles. Angular momentum is and since it is less than half full, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J=0 \!} .
Since the equations has the same form (same commutation relationships) as in the case of orbital angular momentum, we can easily extend everything:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{J}^2&|j,m \rangle = \hbar^{2} j(j+1)|j,m \rangle\\ J_z & |j,m \rangle = \hbar m|j,m \rangle;\;\;\;\;\;-j\le m\le j \\ J_{\pm} & |j,m \rangle = \hbar \sqrt{j(j+1)-m(m\pm 1)}|j,m \pm 1 \rangle\\ \end{align}}
One important feature is that the allowed values for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\!} are integers or half-integers (See Shankar). Therefore the possible values for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j\!} are
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} j=0,\;1/2,\;1,\;3/2,\;2,\;5/2... \end{align}}
We can construct the following table:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c|r|r|r|r|r|r|r} j \rightarrow& 0 & 1/2 & 1 & 3/2 & 2 & 5/2 & ...\\ \hline m& 0 & 1/2 & 1 & 3/2 & 2 & 5/2 & ...\\ \downarrow& &-1/2 & 0 & 1/2 & 1 & 3/2 & \\ & & &-1 &-1/2 & 0 & 1/2 & \\ & & & &-3/2 &-1 &-1/2 & \\ & & & & &-2 &-3/2 & \\ & & & & & &-5/2 & \\ \hline &(2\cdot 0+1)&(2\cdot \frac{1}{2}+1)&(2\cdot1+1)&(2\cdot \frac{3}{2}+1)&(2\cdot2+1)&(2\cdot \frac{5}{2}+1)&(2\cdot j+1) \\ &=1 &=2 &=3 &=4 &=5 &=6 &\\ \hline \end{array}}
Each of these columns represent subspaces of the basis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j,m \rangle \!} that diagonalize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{J}^{2}\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_z \!} . For orbital angular momentum the allowed values for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\!} are integers. This is due to the periodicity of the azimuthal angle.For electrons, they have an additional degree of freedom which takes values "up" or "down". Physically this phenomena appears when the electron is exposed to magnetic fields. Since the coupling with the magnetic field is via magnetic moment, it is natural to consider this degree of freedom as internal angular momentum. Since there are just 2 states, therefore, the angular momentum is represented by the subspace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=1/2\!} .
It is important to see explicitly the representation of this group. Namely we want see the matrix elements of the operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{J}^2 \! } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_x \!} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_y \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_z \!} . The procedure is as follow:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{J}^{2}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_z \!} are diagonal since the basis are their eigenvectors.
- To find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_x\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_y\!} , we use the fact that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} J_x&=\frac{1}{2}[J_+ + J_- ]\\ J_y&=\frac{1}{2i}[J_+ - J_- ]\\ \end{align}}
And the matrix elements of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{\pm} \!} are given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle j',m'|J_{\pm}|j,m\rangle &= \langle j',m'|\hbar \sqrt{j(j+1)-m(m\pm1)}|j,m\pm 1\rangle \\ &= \hbar \sqrt{j(j+1)-m(m\pm1)}\delta_{j' j} \delta_{m' m\pm 1} \\ \end{align}}
Let's find the representations for the subspaces Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=0,\frac{1}{2}\!} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \!}
Subspace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=0} : (matrix 1x1)- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{J}^{2}=0 \!}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_z=0 \!}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle 00|J_{\pm}|00\rangle =0 \;\;\;\rightarrow\;\;\;J_x=J_y=0 \!}
Subspace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=1/2} : (matrix 2x2)- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{J}^{2}= \begin{array}{r|c|c} & |1/2,1/2\rangle & |1/2,-1/2\rangle \\ \hline \langle 1/2,1/2| & \frac{3}{4}\hbar^{2} & 0 \\ \hline \langle 1/2,-1/2| & 0 & \frac{3}{4}\hbar^{2} \\ \hline \end{array} =\frac{3}{4}\hbar^{2} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_z= \begin{array}{r|c|c} & |1/2,1/2\rangle & |1/2,-1/2\rangle \\ \hline \langle 1/2,1/2| & \frac{1}{2}\hbar & 0 \\ \hline \langle 1/2,-1/2| & 0 & -\frac{1}{2}\hbar \\ \hline \end{array} =\frac{1}{2}\hbar \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} }
- For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_+ \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_- \!} are given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} J_+ & = \hbar \sqrt{\frac{1}{2}\left(\frac{1}{2}+1\right)-m(m+1)}\;\;\;\delta_{\frac{1}{2},\frac{1}{2}} \delta_{m',m+1}\\ &=\begin{array}{r|c|c} & |1/2,1/2\rangle & |1/2,-1/2\rangle \\ \hline \langle 1/2,1/2| & 0 & \hbar \sqrt{\frac{1}{2}\left(\frac{1}{2}+1\right)-\left(-\frac{1}{2}\right)\left((-\frac{1}{2})+1\right)} \\ \hline \langle 1/2,-1/2| & 0 & 0 \\ \hline \end{array} =\hbar \begin{pmatrix} 0 & 1 \\ 0 & 0\\ \end{pmatrix} \end{align}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} J_- & = \hbar \sqrt{\frac{1}{2}\left(\frac{1}{2}+1\right)-m(m-1)}\;\;\;\delta_{\frac{1}{2},\frac{1}{2}} \delta_{m',m-1}\\ &=\begin{array}{r|c|c} & |1/2,1/2\rangle & |1/2,-1/2\rangle \\ \hline \langle 1/2,1/2| & 0 & 0\\ \hline \langle 1/2,-1/2| & \hbar \sqrt{\frac{1}{2}\left(\frac{1}{2}+1\right)-\left(\frac{1}{2}\right)\left((\frac{1}{2})-1\right)} & 0 \\ \hline \end{array} =\hbar \begin{pmatrix} 0 & 0 \\ 1 & 0\\ \end{pmatrix} \end{align}}
- The matrices for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_x \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_y \!} are given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} J_x & = \frac{1}{2}[J_+ + J_- ] =\frac{1}{2}\left [ \hbar\begin{pmatrix} 0 & 1 \\ 0 & 0\\ \end{pmatrix} + \hbar\begin{pmatrix} 0 & 0 \\ 1 & 0\\ \end{pmatrix} \right ]\\ &=\frac{\hbar}{2}\begin{pmatrix} 0 & 1 \\ 1 & 0\\ \end{pmatrix}\\ J_y & = \frac{1}{2i}[J_+ - J_- ] =\frac{1}{2i}\left [ \hbar\begin{pmatrix} 0 & 1 \\ 0 & 0\\ \end{pmatrix} - \hbar\begin{pmatrix} 0 & 0 \\ 1 & 0\\ \end{pmatrix} \right ]\\ &=\frac{\hbar}{2i}\begin{pmatrix} 0 & 1 \\ -1 & 0\\ \end{pmatrix} =\frac{\hbar}{2}\begin{pmatrix} 0 & -i \\ i & 0\\ \end{pmatrix} \end{align}}
Subspace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=1} : (matrix 3x3)- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{J}^{2}= \begin{array}{r|c|c|c} & |1,1\rangle & |1,0\rangle & |1,-1\rangle \\ \hline \langle 1,1| & 2\hbar^{2} & 0 &0 \\ \hline \langle 1,0| & 0 & 2\hbar^{2} &0 \\ \hline \langle 1,-1| & 0 & 0 &2\hbar^{2} \\ \hline \end{array} =2\hbar^{2} \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{pmatrix} }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_z = \begin{array}{r|c|c|c} & |1,1\rangle & |1,0\rangle & |1,-1\rangle \\ \hline \langle 1,1| & \hbar & 0 &0 \\ \hline \langle 1,0| & 0 & 0 &0 \\ \hline \langle 1,-1| & 0 & 0 &-\hbar \\ \hline \end{array} =\hbar \begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & -1\\ \end{pmatrix} }
- For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_+ \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_- \!} are given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} J_+ & = \hbar \sqrt{1(1+1)-m(m+1)}\;\;\;\delta_{1,1} \delta_{m',m+1}\\ &=\begin{array}{r|c|c|c} & |1,1\rangle & |1,0\rangle & |1,-1\rangle \\ \hline \langle 1,1| & 0 & \hbar \sqrt{1(1+1)-0(0+1)} &0 \\ \hline \langle 1,0| & 0 & 0 &\hbar \sqrt{1(1+1)-(-1)((-1)+1)} \\ \hline \langle 1,-1| & 0 & 0 &0 \\ \hline \end{array} =\hbar \begin{pmatrix} 0 & \sqrt{2} & 0\\ 0 & 0 & \sqrt{2}\\ 0 & 0 & 0\\ \end{pmatrix} \end{align} }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} J_- & = \hbar \sqrt{1(1+1)-m(m-1)}\;\;\;\delta_{1,1} \delta_{m',m-1}\\ &=\begin{array}{r|c|c|c} & |1,1\rangle & |1,0\rangle & |1,-1\rangle \\ \hline \langle 1,1| & 0 & 0 &0 \\ \hline \langle 1,0| &\hbar \sqrt{1(1+1)-1(1-1)} & 0 &0 \\ \hline \langle 1,-1| & 0 &\hbar \sqrt{1(1+1)-0(0-1)} &0 \\ \hline \end{array} =\hbar \begin{pmatrix} 0 & 0 & 0\\ \sqrt{2} & 0 & 0\\ 0 & \sqrt{2} &0 \\ \end{pmatrix} \end{align}}
- The matrices for and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_y \!} are given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} J_x & = \frac{1}{2}[J_+ + J_- ] =\frac{1}{2}\left [ \hbar \begin{pmatrix} 0 & \sqrt{2} & 0\\ 0 & 0 & \sqrt{2}\\ 0 & 0 & 0\\ \end{pmatrix} + \hbar \begin{pmatrix} 0 & 0 & 0\\ \sqrt{2} & 0 & 0\\ 0 & \sqrt{2} &0 \\ \end{pmatrix} \right ]\\ &=\frac{\hbar}{\sqrt{2}} \begin{pmatrix} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0 \\ \end{pmatrix}\\ J_y & = \frac{1}{2i}[J_+ - J_- ] =\frac{1}{2i}\left [ \hbar \begin{pmatrix} 0 & \sqrt{2} & 0\\ 0 & 0 & \sqrt{2}\\ 0 & 0 & 0\\ \end{pmatrix} - \hbar \begin{pmatrix} 0 & 0 & 0\\ \sqrt{2} & 0 & 0\\ 0 & \sqrt{2} &0 \\ \end{pmatrix} \right ]\\ &=\frac{\hbar}{\sqrt{2}i} \begin{pmatrix} 0 & 1 & 0\\ -1 & 0 & 1\\ 0 & -1 & 0 \\ \end{pmatrix} =\frac{\hbar}{\sqrt{2}} \begin{pmatrix} 0 & -i & 0\\ i & 0 & -i\\ 0 & i & 0 \\ \end{pmatrix} \end{align}}
Summary
The following table is the summary of above calculations.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{r|c|c|c|c|c|c|c|c} & j=0 & j=1/2 &j=1 \\ \hline \mathbf{J}^{2} &0 &\frac{3}{4}\hbar^{2} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} &2\hbar^{2} \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{pmatrix}\\ \hline J_z &0 &\frac{\hbar}{2} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} &\hbar \begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & -1\\ \end{pmatrix}\\ \hline J_x &0 &\frac{\hbar}{2} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} &\frac{\hbar}{\sqrt{2}} \begin{pmatrix} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0\\ \end{pmatrix}\\ \hline J_y &0 &\frac{\hbar}{2} \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} &\frac{\hbar}{\sqrt{2}} \begin{pmatrix} 0 & -i & 0\\ i & 0 & -i\\ 0 & i & 0\\ \end{pmatrix}\\ \hline \end{array} }
Spin 1/2 Angular Momentum
Many particles, such as the electron, proton and neutron, exhibit an intrinsic angular momentum, which unlike orbital angular momentum, has no relation with the spatial degrees of freedom. These are called spin 1/2 particles. An important concept about spin is that it is a purely quantum mechanical construct, with no classical analog, and it cannot be described by a differential operator. The angular momentum of a stationary spin 1/2 particle is found to be quantized to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm\frac{\hbar}{2}} regardless of the direction of the axis chosen to measure the angular momentum. This means that there is a vector operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}=(S_x, S_y, S_z)} and when it projected along an arbitrary axis satisfies the following equations:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}\cdot\hat{m}|\hat{m}\uparrow\rangle = \frac{\hbar}{2}|\hat{m}\uparrow\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}\cdot\hat{m}|\hat{m}\downarrow\rangle = -\frac{\hbar}{2}|\hat{m}\downarrow\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\hat{m}\uparrow\rangle} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\hat{m}\downarrow\rangle} form a complete basis, which means that any state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\hat{n}\uparrow\rangle} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\hat{n}\downarrow\rangle} with different quantization axis can be expanded as a linear combination of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\hat{m}\uparrow\rangle} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\hat{m}\downarrow\rangle} .
The spin operator obeys the standard angular momentum commutation relations
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [S_{\mu}, S_{\nu}]=i\hbar\epsilon_{\mu\nu\lambda}S_{\lambda}\Rightarrow [S_{x}, S_{z}]=-i\hbar S_{y}}
The most commonly used basis is the one which diagonalizes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}\cdot \hat{z} = S_{z}} .
By acting on the states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\hat{z}\uparrow\rangle} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\hat{z}\downarrow\rangle \!} with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_z \!} , we find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{z}|\hat{z}\uparrow\rangle = \frac{\hbar}{2}|\hat{z}\uparrow\rangle} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{z}|\hat{z}\downarrow\rangle = -\frac{\hbar}{2}|\hat{z}\downarrow\rangle}
Now by acting to the left with another state, we can form a 2x2 matrix.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} S_{z} & =\left( \begin{array}{ll} \langle\hat{z}\uparrow|S_{z}|\hat{z}\uparrow\rangle & \langle\hat{z}\uparrow|S_{z}|\hat{z}\downarrow\rangle \\ \langle\hat{z}\downarrow|S_{z}|\hat{z}\uparrow\rangle & \langle\hat{z}\downarrow|S_{z}|\hat{z}\downarrow\rangle \end{array} \right)\\ & =\left(\begin{array}{ll} \hbar/2 & 0 \\ 0 & -\hbar/2 \end{array}\right)\\ & =\dfrac{\hbar}{2}\left( \begin{array}{ll} 1 & 0 \\ 0 & -1 \end{array}\right)\\ &=\dfrac{\hbar}{2}\sigma_{z} \end{align}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal\sigma_{z}} is the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z \!} component of Pauli spin matrix. Repeating the steps (or applying the commutation relations), we can solve for the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \! } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y \!} components.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{x}=\dfrac{\hbar}{2}\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array} \right)=\dfrac{\hbar}{2}\sigma_{x}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{y}=\dfrac{\hbar}{2}\left( \begin{array}{ll} 0 & -i \\ i & 0 \end{array} \right)=\dfrac{\hbar}{2}\sigma_{y}}
In this basis, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S} = \frac{\hbar}{2} \vec{\sigma} \!} . It should be noted that a spin lying along an axis may be rotated to any other axis using the proper rotation operator.
Properties of the Pauli Spin MatricesEach Pauli matrix squared produces the unity matrix
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_{x}^2=\sigma_{y}^2=\sigma_{z}^2=\left( \begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array} \right)}
The commutation relation is as follows
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{[\sigma_{\mu}, \sigma_{\nu}]}=2i\epsilon_{\mu\nu\lambda}\sigma_{\lambda}}
and the anticommutator relation
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\sigma_{\mu}, \sigma_{\nu} \}= [ \sigma_{\mu}, \sigma_{\nu} ]_+ = \sigma_{\mu}\sigma_{\nu}+\sigma_{\nu}\sigma_{\mu}=2\delta_{\mu\nu} \left( \begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array} \right)}
For example,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_{\mu}\sigma_{\nu}=\frac{1}{2}\left\{\sigma_{\mu}, \sigma_{\nu}\right\} + \frac{1}{2}\left[\sigma_{\mu}, \sigma_{\nu}\right] = i\epsilon_{\mu\nu\lambda}\sigma_{\lambda} + \delta_{\mu\nu}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{\mu}S_{\nu}=\dfrac{\hbar^2}{4}\delta_{\mu\nu}+\dfrac{i\hbar}{2}\epsilon_{\mu\nu\lambda}S_{\lambda}}
The above equation is true for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/2\!} spins only!!
In general,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} (\vec{a} \cdot \vec\sigma)(\vec{b}\cdot\vec\sigma) & =(a_{x}\sigma_{x}+a_{y}\sigma_{y}+a_{z}\sigma_{z})(b_{x}\sigma_{x}+b_{y}\sigma_{y}+b_{z}\sigma_{z})\\ & = a_{\mu}\sigma_{\mu}b_{\nu}\sigma_{\nu}\\ & =a_{\mu}b_{\nu}\sigma_{\mu}\sigma_{\nu}\\ & =a_{\mu}b_{\nu} \left( \left( \begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array} \right) \delta_{\mu\nu} + i\epsilon_{\mu\nu\lambda}\sigma_{\lambda} \right)\\ & = \left( \begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array} \right) \vec{a}\cdot \vec{b} + i(\vec{a} \times \vec{b})\cdot\vec{\sigma} \end{align}}
Finally, any Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \times 2 \!} matrix can be written in the form
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M=\alpha \left( \begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array} \right) +\vec\beta \cdot \vec\sigma= \left( \begin{array}{ll} M_{11} & M_{12} \\ M_{21} & M_{22} \end{array} \right) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow\alpha=\frac{1}{2}\left(M_{11}+M_{22}\right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow\beta_{x}=\frac{1}{2}\left(M_{12}+M_{21}\right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow\beta_{y}=\frac{i}{2}\left(M_{12}-M_{21}\right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow\beta_{z}=\frac{1}{2}\left(M_{11}-M_{22}\right)}
For infinitesimal Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\alpha}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}=\hat{m}+\vec{\alpha} \times \hat{m} + O(\alpha^2)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \vec{S}\cdot\hat{n}=\vec{S}\cdot\hat{m}+\vec{S} \cdot(\vec{\alpha} \times \vec{m})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow S_{\mu}\hat{n}_{\mu} = S_{\mu}\hat{m}_{\mu} + S_{\mu}\epsilon_{\mu\nu\lambda}\alpha_{\nu}\hat{m}_{\lambda}}
Note that using the previous developed formulas, we find that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{\mu}\epsilon_{\mu\nu\lambda}=\frac{1}{i\hbar} \left[S_{\nu}, S_{\lambda}\right] }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \Rightarrow \vec{S}\cdot\hat{n} & =\vec{S}\cdot\hat{m}+\frac{1}{i\hbar}[\vec{\alpha}\cdot\vec{S}, \hat{m}\cdot\vec{S}] \\ & =\vec{S}\cdot\hat{m}+\frac{i}{\hbar}[\vec{S}\cdot\hat{m}, \vec{S}\cdot\vec{\alpha}] \end{align} }
To this order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\alpha}} , this equation is equivalent to
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}\cdot\hat{n}=e^{-\frac{i}{\hbar}\vec{S}\cdot\vec{\alpha}} \left(\vec{S}\cdot\hat{m}\right) e^{\frac{i}{\hbar}\vec{S}\cdot\vec{\alpha}}} .
This equation is exact for any Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec\alpha \!} not just infinitesimal Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec\alpha \!} just as in hte case of orbital angular momentum.
Consider Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S} \cdot \hat{n} \!} acts on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\frac{i}{\hbar} \vec{S} \cdot {\alpha}} \left| \hat{m} \uparrow \right\rangle \!} which is an eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S} \cdot \hat{n} \!} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \vec{S}\cdot\hat{n} \left( e^{-\frac{i}{\hbar}\vec{S}\cdot\vec{\alpha}} |\hat{m} \uparrow\rangle \right) & = e^{-\frac{i}{\hbar} \vec{S}\cdot\vec{\alpha}} \left( \vec{S}\cdot\hat{m} \right) \left|\hat{m} \uparrow\right\rangle \\ & = \frac{\hbar}{2}\left( e^{-\frac{i}{\hbar}\vec{S}\cdot\vec{\alpha}} |\hat{m} \uparrow\rangle \right) \end{align} }
Another way of expressing the rotation of the spin basis by an angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec \alpha} about some axis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\alpha}} (and the one derived in class) is the following.Consider an operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\frac{i}{\hbar}\vec{S}\cdot\vec{\alpha}}} from the previous equation. This can also be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} e^{-\frac{i}{\hbar}\vec{S}\cdot\vec{\alpha}} & = e^{-\frac{i}{2}\vec{\sigma}\cdot\vec{\alpha}} \\ & = 1 - \frac{i}{2} \vec{\sigma}\cdot\vec{\alpha} + \frac{1}{2}\left(-\frac{i}{2}\vec{\sigma}\cdot\vec{\alpha}\right)^2 + \cdots \\ & = \sum_{n=0}^{\infty} \frac{1}{n!} \left(-\frac{i}{2} \vec{\sigma}\cdot\vec{\alpha}\right)^n \\ & = \sum_{n=0}^{\infty} \frac{(-i)^n}{n! 2^n} |\vec{\alpha}|^n \left( \vec{\sigma}\cdot\hat{\alpha}\right)^n \end{align} } .
Consider, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \left( \vec{\sigma}\cdot\hat{\alpha} \right)^2 & = \left(\sigma_x \alpha_x + \sigma_y \alpha_y + \sigma_z \alpha_z \right)\left(\sigma_x \alpha_x + \sigma_y \alpha_y + \sigma_z \alpha_z\right) \\ & = \left(\alpha_x ^2 + \alpha_y ^2 + \alpha_z ^2 \right) + \alpha_x \alpha_y \left(\sigma_x \sigma_y + \sigma_y \sigma_x\right) + \alpha_x \alpha_z \left(\sigma_x \sigma_z + \sigma_z \sigma_x\right) + \alpha_y \alpha_z \left(\sigma_y \sigma_z + \sigma_z \sigma_y\right) \\ & = 1 \end{align} } .
The non-squared terms vanish because of the anti-commutation property of the Pauli matrices.
Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\vec{\sigma}\cdot\hat{\alpha})^{2n} = 1} (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \!} is an integer), thus the above equation can be split:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} e^{-\frac{i}{\hbar}\vec{S}\cdot\vec{\alpha}} & = \sum_{n = even}^{\infty} \frac{(-i)^{n}}{n!2^n}\left|\vec{\alpha}\right|^n + \vec{\sigma}\cdot\hat{\alpha} \sum_{n = odd}^{\infty} \frac{(-i)^n}{n!2^n} \left| \vec{\alpha} \right|^n \\ & = \cos\left(\frac{\left|\vec\alpha\right|}{2}\right) - i \vec{\sigma}\cdot\hat{\alpha} \sin\left(\frac{\left|\vec\alpha\right|}{2}\right) \end{align} }
This form may be more convenient when performing rotations. A solved problem for spins
A Solved Problem on General Spin Vectors.
Addition of angular momenta
Formalism
In order to consider the addition of angular momentum, consider two angular momenta, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_1 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_2 } which belong to two different subspaces. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_1 } has a Hilbert space of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(2 j_{1} + 1\right)} states, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_2 } has a Hilbert space of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(2 j_{2} + 1\right)} states. The total angular momentum is then given by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}=\vec{J}_{1}+\vec{J}_{2}=\vec{J}_{1}\otimes\mathbb{I}_1 + \mathbb{I}_2\otimes\vec{J}_{2} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad (6.1.1)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}_1 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}_2 } are the identity matrices of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_{1}} 's and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_{2}} 's Hilbert spaces, and where the dimension Hilbert space is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!(2j_1+1)(2j_2+1)} .The components of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_1 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_2 } obey the commutation relation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[J_{1\mu}, J_{1\nu}\right] = i\hbar\epsilon_{\mu\nu\lambda} J_{1\lambda} \qquad \qquad \left[J_{2\mu}, J_{2\nu}\right] = i\hbar\epsilon_{\mu\nu\lambda} J_{2\lambda} \qquad \qquad \qquad \qquad \qquad \qquad\;\ (6.1.2a)}
And since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_1 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_2 } belong to different Hilbert spaces:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[J_{1\mu}, J_{2\nu}\right] = 0 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\; (6.1.2b)}
Given the simultaneous eigenkets of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_1^2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!J_{1z}} denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 m_1\rangle} , and of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_2^2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!J_{2z}} denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_2 m_2\rangle} we have the following relations:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_1^2|j_1 m_1\rangle = j_1(j_1+1)\hbar|j_1 m_1\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{1z}|j_1 m_1\rangle = m_1\hbar|j_1 m_1\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_2^2|j_2 m_2\rangle = j_2(j_2+1)\hbar|j_2 m_2\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{2z}|j_2 m_2\rangle = m_2\hbar|j_2 m_2\rangle }
Now looking at the two subspaces together, the operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_1^2} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!J_{1z}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_2^2} , can be simultaneously diagonalized by their join eigenstates. These eigenstates can be formed by the direct products of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 m_1\rangle } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_2 m_2\rangle } :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 m_1\rangle \otimes |j_2 m_2\rangle = |j_1,j_2; m_1,m_2\rangle }
This basis for the total system diagonalizes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_1^2 \!} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!J_{1z}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_2^2 \! } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!J_{2z}} , but these four operators DO NOT define the total angular momentum of the system. Therefore it is useful to relate these direct product eigenstates to the total angular momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J} = \vec{J}_{1} + \vec{J}_{2}} .
Recall that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{z} = J_{1z} + J_{2z} \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[J_{\mu}, J_{\nu}\right] = i\hbar\epsilon_{\mu\nu\lambda} J_{\lambda}} .
We also know the relations: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[J_{1,2}^2, J^2\right]=0 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[J_{1,2}^2, J_{z}\right] = 0 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[J^{2}, J_{z}\right] = 0 }
This tells us that we have a set of four operators that commute with each other. From this we can specify Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{1}^2 , J_{2}^2 , J^2} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{z}\!} simultaneously. The joint eigenstates of these four operators denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j m j_1 j_2\rangle} . These four operators operate on the base kets according to:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J^2|j m j_1 j_2\rangle = \hbar^2 j(j + 1)|j m j_1 j_2\rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\;\;\;\; (6.1.7)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{z}|j m j_{1} j_{2}\rangle=\hbar m |j m j_{1} j_{2}\rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\;\;\;\;\;\ (6.1.8)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{1,2}^2|j m j_{1} j_{2}\rangle=\hbar^2 j_{1,2}(j_{1,2}+1) |j m j_{1} j_{2}\rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\;\;\ (6.1.9)}
The choice of basis is now dictated by the specific problem being solved because we can find the relationship between the direct product basis and total-Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J \!} basis.
For example, consider two spin 1/2 particles with basis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\uparrow\uparrow\rangle, |\uparrow\downarrow\rangle, |\downarrow\uparrow\rangle ,} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\downarrow\downarrow\rangle } . These states are eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{1}^2, J_{2}^2, J_{1z},\!} andFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{2z}\!} , but are they eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!J^2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_z^2} ?
Let us see what happens with the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\uparrow\downarrow\rangle} :Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J^2 |\uparrow\downarrow\rangle = \left(J_{x}^2+J_{y}^2+J_{z}^2\right)|\uparrow\downarrow\rangle = \left((J_{x}+iJ_{y})(J_{x}-iJ_{y})+i[J_{x}, J_{y}] + J_{z}^2 \right)|\uparrow\downarrow\rangle} .
Let's define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{\pm}=(J_{x}\pm iJ_{y})} , then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J^2 |\uparrow\downarrow\rangle =\left(J_{+}J_{-}-\hbar J_{z} + J_{z}^2 \right)| \uparrow\downarrow\rangle = \left((J_{1+}+J_{2+})(J_{1-}+J_{2-})+(J_{1z}+J_{2z})^2-\hbar (J_{1z}+J_{2z})\right)|\uparrow\downarrow\rangle }
Now Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (J_{1z}+J_{2z}) |\uparrow\downarrow\rangle = \left(\frac{\hbar}{2}-\frac{\hbar}{2}\right) |\uparrow\downarrow\rangle = 0 }
Also, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (J_{1+}+J_{2+})(J_{1-}+J_{2-})|\uparrow\downarrow\rangle = (J_{1+}+J_{2+})|\downarrow\downarrow\rangle = |\uparrow\downarrow\rangle + |\downarrow\uparrow\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore J^2 |\uparrow\downarrow\rangle = |\uparrow\downarrow\rangle + |\downarrow\uparrow\rangle }
Which means that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\uparrow\downarrow\rangle } is not an eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!J^2} . Similarly, it can be shown that the other three states are also not eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!J^2} .
To find a relationship between the direct product basis and the total-Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J \!} basis, begin by finding the maximum total Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m \!} state:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|j =1, m=1; \frac{1}{2}, \frac{1}{2}\right\rangle = |\uparrow \uparrow\rangle }
This must be true because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\uparrow \uparrow\rangle } is the only state with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!m = 1 } . Now we can lower this state using Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{-} \!} to yield:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|j =1, m=0; \frac{1}{2}, \frac{1}{2}\right\rangle = \frac{1}{\sqrt{2}}\left(|\uparrow \downarrow\rangle + |\downarrow \uparrow\rangle\right) }
And then lower this state to yield:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|j =1, m=-1; \frac{1}{2}, \frac{1}{2}\right\rangle = |\downarrow \downarrow\rangle }
All we are missing now is the antisymmetric combination of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\uparrow \downarrow\rangle} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\downarrow \uparrow\rangle)} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|j =0, m=0; \frac{1}{2}, \frac{1}{2}\right\rangle = \frac{1}{\sqrt{2}}\left(|\uparrow \downarrow\rangle - |\downarrow \uparrow\rangle\right) }
We now have a relationship between the two bases. Also, we can write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\frac{1}{2}} \otimes \mathbf{\frac{1}{2}} = \mathbf{1} \otimes \mathbf{0} \! } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{1} \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{0} \! } represent triplet state and single state respectively.
Problem: CG coefficients[[2]]
Another problem: CG coefficients[[3]]
Clebsch-Gordan Coefficients
Now that we have constructed two different bases of eigenkets, it is imperative to devise a way such that eigenkets of one basis may be written as linear combinations of the eigenkets of the other basis. To achieve this, we write:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j m j_1 j_2\rangle = \sum_{m_1,m_2}|j_1 j_2 m_1 m_2\rangle\langle j_1 j_2 m_1 m_2|j m j_1 j_2\rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\ (6.2.1) }
In above, we have used the completeness of the basis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 j_2 m_1 m_2\rangle} , given by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{m_1,m_2}|j_1 j_2 m_1 m_2\rangle\langle j_1 j_2 m_1 m_2| = 1 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad\;\;\; (6.2.2)}
The coefficients Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle j_1 j_2 m_1 m_2|j m j_1 j_2\rangle} are called Clebsch-Gordan coefficients (for an extensive list of these coefficients, see here), which have the following properties, giving rise to two "selection rules":
1. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m \neq m_1 + m_2} , then the coefficients vanish.
- Proof: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \because J_z = J_{1z} + J_{2z}} , we get
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (J_z - J_{1z} - J_{2z})|j m j_1 j_2\rangle = 0}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \langle j_1 j_2 m_1 m_2|(J_z - J_{1z} - J_{2z})|j m j_1 j_2\rangle = 0}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore (m - m_1 - m_2)\langle j_1 j_2 m_1 m_2|j m j_1 j_2 \rangle = 0 } . Q.E.D.
2. The coefficients vanish, unless Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 - j_2| \le j \le j_1 + j_2 }
- This follows from a simple counting argument. Let us assume, without any loss of generality, that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! j_1 > j_2 } . The dimensions of the two bases should be the same. If we count the dimensions using the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 j_2 m_1 m_2\rangle } states, we observe that for any value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! j } , the values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! m } run from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! -j} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! j } . Therefore, for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! j_1 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! j_2 } , the number of eigenkets is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! (2j_1 + 1)(2j_2 + 1) } . Now, counting the dimensions using the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j m j_1 j_2 \rangle } eigenkets, we observe that, again, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! m } runs from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! -j } to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! j } . Therefore, the number of dimensions is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = \sum_a^b (2j + 1) } . It is easy to see that for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! a = j_1 - j_2 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! b = j_1 + j_2.} Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = (2j_1 + 1)(2j_2 +1)\!} .
Further, it turns out that, for fixed Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!j_1} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!j_2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!j} , coefficients with different values for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!m_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!m_2} are related to each other through recursion relations. To derive these relations, we first note that: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{\pm}|j m j_1 j_2\rangle = \sqrt{(j \mp m)(j \pm m + 1)}\hbar |j m \pm 1 j_1 j_2\rangle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\;\ (6.2.3) }
Now we write, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{\pm}|j m j_1 j_2 \rangle = (J_{1 \pm} + J_{2 \pm}) \sum_{m_1,m_2}|j_1 j_2 m_1 m_2 \rangle \langle j_1 j_2 m_1 m_2|j m j_1 j_2 \rangle \qquad \qquad \qquad \qquad (6.2.4)}
Using equation #(6.2.4), we get (with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1 \to m'_1 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_2 \to m'_2 } ):
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} & \sqrt{(j \mp m)(j \pm m + 1)}|j m \pm 1 j_1 j_2 \rangle \\ & = \sum_{m'_1,m'_2} \left( \sqrt{(j_1 \mp m'_1)(j_1 \pm m'_1 + 1)}|j_1 j_2 m'_1 \pm 1 m'_2 \rangle + \sqrt{(j_2 \mp m'_2)(j_2 \pm m'_2 + 1)}|j_1 j_2 m'_1 m'_2 \pm 1 \rangle \right)\langle j_1 j_2 m'_1 m'_2|j m j_1 j_2 \rangle \end{align}}
The Clebsch-Gordan coefficients form a unitary matrix, and by convention, they are all taken real. Any real unitary matrix is orthogonal, as we study below.Example
As an example lets calculate some Clebsch-Gordan coefficients through applications of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{\plusmn}=S_x+iS_y} on the states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |Sm_s> } .
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=S_1+S_2} be the total angular momentum of two spin 1/2 particles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (S_1=S_2=1/2) } . Calculate the Clebsch-Gordan coefficientsFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <m_1m_2|Sm_s> } by successive applications of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{\plusmn}=S_x+iS_y } on the states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |Sm_s> } . Work separately in the two subspaces S=1 and S=0.
In order to find the coefficients for the addition of spin 1/2, we shall use the following relations:
I Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{\plusmn}|Sm_s> = \hbar\sqrt{S(S+1)-m_s(m_s\plusmn 1)}|Sm_s\plusmn 1>}
II Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{1\plusmn}|m_1m_2> = \hbar\sqrt{S_1(S_1+1)-m_1(m_1\plusmn 1)}|m_1\plusmn 1 m_2>}
IIIFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{2\plusmn}|m_1m_2> = \hbar\sqrt{S_2(S_2+1)-m_2(m_2\plusmn 1)}|m_1 m_2\plusmn 1>}
We shall also use the phase condition
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |S=S_1+S_2,m_s=\plusmn(S_1+S_2)> = |m_1=\plusmn S_1,m_2=\plusmn S_2> }
Note: The states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |S=S_1=S_2,m_s=\plusmn (S_1+S_2)> } are eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^2 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_z } , with nondegenerate eigenvalues Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{\plusmn} = \plusmn \hbar(S_1+S_2) } , repsectively. Therefore,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |S=S_1+S_2,m_s=\plusmn(S_1+S_2)> = e^{i \phi}|m_1=\plusmn S_1,m_2=\plusmn S_2> }
and the phase Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} may be chosen to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi =0} .
i Subspace S=1: From the phase condition we immediately have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1,1>=|1/2,1/2>=|++> }Then, operating with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_-=S_{1-}+S_{2-} } on both sides of this, and using II and III, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{-}|1,1>=\hbar\sqrt{1(1+1)-1(1-1)}|1,0>=\hbar\sqrt{2}|1,0>} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{-}|1,1>=(S_{1-}+S_{2-})|1/2,1/2>=\hbar\sqrt{1}|-1/2,1/2>+\hbar|1/2,-1/2>}
Thus, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1,0>=\frac{1}{\sqrt{2}}(|1/2,-1/2>+|-1/2,1/2>) = \frac{1}{\sqrt{2}}(|+->+|-+>) }
Similarly, operating with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{-} } once again on the state |1,0>, we find
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{-}|1,0> = \hbar\sqrt{1(1+1)-0(0-1)}|1,-1>=\hbar\sqrt{2}|1,-1>} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{-}|1,0> = \frac{1}{\sqrt{2}}S_{1-}(|1/2,-1/2>+|-1/2,1/2>)+\frac{1}{\sqrt{2}}S_{2-}(|1/2,-1/2>+|-1/2,1/2>) } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{\hbar}{\sqrt{2}}(|-1/2,-1/2>+|-1/2,-1/2>) = \frac{2}{\sqrt{2}}|-1/2,-1/2>}
Therefore, in accordance with the phase condition, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1,-1> = |-1/2,-1/2> = |--> }
ii Subspace S=0: Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_s = m_1 + m_2} (in this case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_s=0} ), we haveFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0,0> = \alpha|-1/2,1/2>+ \beta |-1/2,1/2> }
Next, due to orthonormality of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |Sm_s> } basis we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <1,0|0,0> = 0 \rightarrow \frac{1}{\sqrt{2}}(\alpha+\beta)=0 \rightarrow \beta=-\alpha }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <0,0|0,0>=1 \rightarrow |\alpha|^2+|\beta|^2=1 \rightarrow 2|\alpha|^2=1 \rightarrow \alpha = \frac{1}{\sqrt{2}} }
Therefore, we find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0,0> = \frac{1}{\sqrt{2}}(|1/2,-1/2>-|-1/2,1/2>) }
Orthogonality of Clebsch-Gordan Coefficients
We have the following symmetry:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle j_1 j_2 m_1 m_2 | j_1 j_2 j m \rangle = (-1)^{j-j_1-j_2} \langle j_2 j_1 m_2 m_1 | j_2 j_1 j m \rangle = \langle j_2 j_1, -m_2, -m_1 |j_2 j_1 j, -m \rangle}
If we put the coefficients into a matrix, it is real and unitary, meaning Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle j m j_1 j_2 |j_1 j_2 m_1 m_2 \rangle = \langle j_1 j_2 m_1 m_2 |j m j_1 j_2 \rangle ^*}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle | j_1 j_2 m_1 m_2 \rangle = \sum_{j,m} |j m j_1 j_2 \rangle \langle j m j_1 j_2 |j_1 j_2 m_1 m_2 \rangle } .
For example,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\uparrow_1 \downarrow_2 \rangle = \dfrac{1}{\sqrt{2}}(|10 \rangle + |00 \rangle )}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\downarrow_1 \uparrow_2 \rangle = \dfrac{1}{\sqrt{2}}(|10 \rangle - |00 \rangle )}
We have the following orthogonality relations:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{jm}\langle j_1 m'_1 j_2 m'_2|jmj_1 j_2\rangle \langle jmj_1 j_2 | j_1 m_1 j_2 m_2\rangle = \delta_{m_1 m'_1} \delta_{m_2 m'_2} }Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{m_1 m_2}\langle j m j_1 j_2|j_1 m_1 j_2 m_2\rangle \langle j_1 m_1 j_2 m_2 | j' m' j_1 j_2\rangle = \delta_{j j'} \delta_{m m'} }
Hydrogen atom with spin orbit coupling given by the following hamiltonian
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H'=\dfrac{e^2}{2m^2 c^2 r^3}\vec{L}\cdot\vec{S}}
Recall, the atomic spectrum for bound states
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n = -\frac{e^2}{2a_o n^2}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=1, 2, 3, ...\!}
The ground state, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1s\rangle} , is doubly degenerate: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\uparrow\downarrow}{1s}}
First excited state is 8-fold degenerate: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\uparrow\downarrow}{1s}\dfrac{\uparrow\downarrow}{}\dfrac{\uparrow\downarrow}{2p}\dfrac{\uparrow\downarrow}{}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \!} -th state is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2n^2\!} fold degenerate.
We can break apart the angular momentum and spin into its Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x, y, z \!} -components
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{L}\cdot\vec{S} = L_x S_x + L_y S_y + L_z S_z }
Define lowering and raising operators
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow L_\pm = L_x \pm iL_y}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{L}\cdot\vec{S} = L_z S_z + \dfrac{1}{2} L_{+} S_{-} + \dfrac{1}{2} L_{-} S_{+} }
For the ground state, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (|1s, \uparrow\rangle, |1s, \downarrow\rangle )} , nothing happens. Kramer's theorem protects the double degeneracy.
For the first excited state, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (|2s, \uparrow\rangle, |2s, \downarrow\rangle )} , once again nothing happens.
For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (|2p, \uparrow\rangle, |2p, \downarrow\rangle )} , there is a four fold degeneracy.
We can express the solutions in matrix form
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( \begin{array}{llllll} \dfrac{\hbar^2}{2} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \dfrac{\hbar^2}{2} \end{array} \right)}
But there is a better and more exact solution, which we can solve for by adding the momenta first.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{L}\cdot\vec{S} = \frac{1}{2} \left(\vec{L} + \vec{S}\right)^2 -\frac{1}{2}\vec{L}^2 -\frac{1}{2}\vec{S}^2 = \frac{1}{2}\left(J^2 -L^2 - S^2\right)}
add the angular momenta:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1s\rangle : l=0, s=\dfrac{1}{2}: 0\otimes \dfrac{1}{2}= \dfrac{1}{2}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |2s\rangle : l=0, s=\dfrac{1}{2}: 0\otimes \dfrac{1}{2}= \dfrac{1}{2}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |2p_m, 0 \rangle : l=1, s=\dfrac{1}{2}: 1\otimes \dfrac{1}{2}= \dfrac{3}{2} \oplus \dfrac{1}{2}}
So that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{L}\cdot\vec{S} \left|j=\dfrac{3}{2}, m, l=1, s=\dfrac{1}{2} \right\rangle =\dfrac{1}{2} \left(\hbar^2\dfrac{3}{2}\dfrac{5}{2}-2 \hbar^2 - \dfrac{3}{4} \hbar^2\right) \left|j=\dfrac{3}{2}, m, l=1, s=\dfrac{1}{2} \right\rangle = \dfrac{\hbar^2}{2} \left| j=\dfrac{3}{2}, m, l=1, s=\dfrac{1}{2} \right\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{L}\cdot\vec{S} \left|j=\dfrac{1}{2}, m, l=1, s=\dfrac{1}{2} \right\rangle =\dfrac{-\hbar^2}{2} \left| j=\dfrac{1}{2}, m, l=1, s=\dfrac{1}{2} \right\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|j=\dfrac{3}{2}, m= \dfrac{3}{2}, l=1, s=\dfrac{1}{2} \right\rangle = \left|l=1, m_l =1 \right\rangle \left|s=\dfrac{1}{2}, m_s = \dfrac{1}{2} \right\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|j= \dfrac{3}{2}, m= \dfrac{3}{2} \right\rangle = \left|m_l =1 \right\rangle \left|m_s = \dfrac{1}{2} \right\rangle }
Define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{-} = L_{-} + S_{-} \!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{-} \left|\dfrac{3}{2}, \dfrac{1}{2} \right\rangle = \left(L_{-} + S_{-} \right)\left|l=1, m=1 \right\rangle \left| S=\frac{1}{2}, m_s=\frac{1}{2} \right\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \hbar \sqrt{\dfrac{3}{2} \dfrac{5}{2}- \dfrac{3}{2}\dfrac{1}{2}} \left|\dfrac{3}{2}, \dfrac{1}{2} \right\rangle = \hbar \sqrt{2} \left|l=1, m=0 \right\rangle \left|s=\frac{1}{2}, m_s=\frac{1}{2} \right\rangle + \hbar \sqrt{\dfrac{1}{2} \dfrac{3}{2} - \frac{1}{2}\left(\frac{1}{2}-1\right)}|l=1,m=1\rangle \left| s=\frac{1}{2}, m_s=-\frac{1}{2} \right\rangle}Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \sqrt{3} \left|\dfrac{3}{2}, \dfrac{1}{2} \right\rangle = \sqrt{2}\left|1,0 \right\rangle \left|\frac{1}{2}, \frac{1}{2}\right\rangle + \left|1,1 \right\rangle \left| \frac{1}{2}, -\frac{1}{2} \right\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \left|\frac{3}{2}, \frac{1}{2} \right\rangle = \sqrt{\frac{2}{3}}\left|1,0 \right\rangle \left|\dfrac{1}{2}, \frac{1}{2} \right\rangle + \sqrt{\dfrac{1}{3}}\left|1,1 \right\rangle \left| \frac{1}{2},- \dfrac{1}{2} \right \rangle}
As the same,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\dfrac{3}{2}, -\dfrac{1}{2} \right\rangle = \sqrt{\dfrac{2}{3}} \left|1,0 \right\rangle \left| \frac{1}{2},-\dfrac{1}{2} \right\rangle + \sqrt{\dfrac{1}{3}}\left|1,-1 \right\rangle \left| \frac{1}{2}, \dfrac{1}{2} \right\rangle} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\dfrac{3}{2}, \pm \dfrac{3}{2} \right\rangle = \left|1, \pm 1 \right \rangle \left| \frac{1}{2}, \pm \dfrac{1}{2} \right\rangle}
We can express as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|j=\dfrac{1}{2}, m =\dfrac{1}{2} \right\rangle = \alpha \left|1,0 \right\rangle \left| \frac{1}{2}, \dfrac{1}{2} \right\rangle + \beta \left|1,1 \right\rangle \left|\frac{1}{2}, -\dfrac{1}{2} \right\rangle } ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|j=\dfrac{1}{2}, m = -\dfrac{1}{2} \right \rangle = \alpha ' \left|1,0 \right\rangle \left|\frac{1}{2},-\dfrac{1}{2} \right\rangle + \beta ' \left|1,-1 \right\rangle \left| \frac{1}{2}, \dfrac{1}{2} \right\rangle } .
When we project these states on the previously found states, we find that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = \dfrac{1}{\sqrt{3}}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = - \sqrt{\dfrac{2}{3}}} ,
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha' = - \dfrac{1}{\sqrt{3}}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta' = \sqrt{\dfrac{2}{3}}} .
For a more detailed account of these and other related results, see here.
Addition of three angular momenta
To add three angular momenta Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_1, \bold J_2, \bold J_3} , first we add Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_{12}=\bold J_1 + \bold J_2} , and construct the simultaneous eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_{1} ^{2}, \bold J_2 ^{2}, \bold J_{12} ^{2}, \bold J_{12z}, \bold J_3 ^{2}, \bold J_{3z}} . We write such states as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 j_2 j_{12} m_{12} j_3 m_3 \rangle} . Such states can be given in terms of Clebsch-Gordan coefficients and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 j_2 j_3 m_1 m_2 m_3 \rangle} (eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_1^{2}, \bold J_2^{2}, \bold J_3^{2}, \bold J_{1z}, \bold J_{2z}, \bold J_{3z}} ):
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 j_2 j_{12} m_{12} j_3 m_3 \rangle = \sum_{m_1,m_2} |j_1 j_2 j_3 m_1 m_2 m_3 \rangle \langle j_1 j_2 j_3 m_1 m_2 m_3|j_1 j_2 j_{12} m_{12} j_3 m_3\rangle}
Next we add Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_{12}} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_3} , forming simultaneous eigenstates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 j_2 j_{12} j_3 j m \rangle} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_1^{2}, \bold J_2^{2}, \bold J_{12}^{2}, \bold J_3^{2}, \bold J^{2}, \bold J_{z}} . These are given in terms of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle | j_1 j_2 j_{12} m_{12} j_3 m_3 \rangle} by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 j_2 j_{12} j_3 j m \rangle = \sum_{m_{12},m_{3}} | j_1 j_2 j_{12} m_{12} j_3 m_3 \rangle \langle j_{12} m_{12} j_3 m_3 | j_{12} j_3 j m \rangle }
Therefore, we can construct eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_1^{2}, \bold J_2^{2}, \bold J_{12}^{2}, \bold J_3^{2}, \bold J^{2}, \bold J_{z}} in terms of eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_1^{2}, \bold J_2^{2}, \bold J_3^{2}, \bold J_{1z}, \bold J_{2z}, \bold J_{3z}} as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j_1 j_2 j_{12} j_3 j m \rangle = \sum_{m_{1},m_{2},m_{3}} |j_1 j_2 j_3 m_1 m_2 m_3 \rangle \sum_{m_{12}} \langle j_1 j_2 m_1 m_2|j_1 j_2 j_{12} m_{12}\rangle \langle j_{12} m_{12} j_3 m_3 | j_{12} j_3 j m \rangle }
Thus the analogous addition coefficients for three angular momenta are products of Clebsch-Gordan coefficients.
Note that for addition of two angular momenta, the dimension of Hilbert space is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!(2J_1 + 1)(2J_2 + 1)} . For three angular momenta, it is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \!(2J_1 + 1)(2J_2 + 1)(2J_3 + 1)} .
Elementary applications of group theory in Quantum Mechanics
Symmetry
Mathematically, A Group is consisted as a set of elements in which a operation is defined to combine any two of the elements to form a third element. Also, the group should satisfy some axioms such as closure, associativity, identity and invertibility.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G=\lbrace A,B,C \dots\rbrace}
G is a group under operation AB if
. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB\in G} ,forFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \forall A,B\in G} (closure)
. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(AB\right)C=A\left(BC\right)} (associativity)
. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \exists \mathbf I} , such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf IA=A\mathbf I=A} , forFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \forall A} (identity)
. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \forall A, \exists A^{-1}} , Such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AA^{-1}=A^{-1}A=\mathbf I } (invertibility)
Broad characteristics of various groups
Discrete and Continuous Groups
G can be discrete(isolated elements) or it can be continuous(rotation)
Examples(discrete group):
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf I_2=\lbrace\mathbf I,A\rbrace} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{2}=\mathbf I}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf I_n=\lbrace n \rbrace} , The operation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle “\circ”} is defined as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\circ m=n+m}
And continuous group:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u\left(1\right)=\lbrace e^{i\theta}; \theta\in\lbrack 0,2\pi\rbrack\rbrace} , in which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i\theta}e^{i\phi}=e^{i\left(\theta+\phi\right)}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SU\left(2\right)} : group of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\times2} matrices with unit determinant (special unitary group)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O\left(3\right)} : group of all rotations about the origin in 3D. i.e. set of all orthogonal transformation in a 3D vector space, or a group of all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3\times3} orthogonal matrices.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SU\left(3\right)} : a group of all unitary matrices with determinant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +1}
Abelian Group
If all the elements commute with each other, then we shall call the group is "Abelian", otherwise it's non-abelian.
In a group Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} ,if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB=BA \forall A,B\in G}
Then the group is said to be abelian.
Example:The addition of real numbers yields an abelian group. However, the group of square matrices with dimension N under multiplication is not abelian.
Continuously Connected
A groups is called continuously connected if a continuous variation of the group parameters leads from any arbitrary element of the group to any other.
Example: The translation group of the elements Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {a = a_{x}\varepsilon_{1}+a_{y}\varepsilon_{2}+a_{z}\varepsilon_{3}}} possesses three continuous parameters Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a_{x},a_{y},a_{z})} .We can generate each displacement vector in space by continuous variation of these parameters. However, rotations combined with reflection in space [called Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O[3]} ], form a continuous,not connected group. similarly, the Lorentz transformation group in relativity for a not connected group.
Definition of conjugate elements: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} is conjugate to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B=XAX^{-1}} for some Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X\in G} . This property is reciprocal since that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=X^{-1}BX}Collecting all conjugate elements gives a conjugacy class. We can divide G into conjugate classes.
Compact Group In each sequence within a compact group there exists an infinite partial sequence Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n}} of group elements, which converges to an element of the group, i.e Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\to\infty}a_{n}=a,a\in G}
Examples, (a) The group of the translation vectors on a lattice Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = {a_{n} = n_{1}\varepsilon_{1}+n_{2}\varepsilon_{2}+n_{3}\varepsilon_{3}}} , with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{1},n_{2},n_{3} \in N}
Theory of group representations
Group representations are the description on abstract objects using linear transformations of vector spaces. Usually, the elements in the group are represent by matrices so that the group operation can be represents by matrix multiplication.
Associate a matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma\left(A\right)} with each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\in G}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma\left(A\right)\Gamma\left(B\right)=\Gamma\left(AB\right)}
Group theory and Quantum Mechanics
Irreducible tensor representations and Wigner-Eckart theorem
Representation of rotations
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J} is the total angular momentum of a system (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J = \bold J_1 + \bold J_2} ), the operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\vec \alpha}=e^{-\frac{i}{\hbar} \bold J \cdot \vec \alpha}} acting to the right on a state of the system, rotates it in a positive sense about the axis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec \alpha} by an angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec \alpha|} . This is similar to how Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\frac{i}{\hbar} \bold L \cdot \vec \alpha}} rotates in the plane, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\frac{i}{\hbar} \bold S \cdot \vec \alpha}} rotates spin states. Suppose that we act with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\vec \alpha}} on an eigenstate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |jm \rangle} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J^2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_z} . This generates a superposition of states. Under the rotation, the state is generally no longer an eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_z} . However, the rotated state remains an eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J^2} , so the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! j } remains the same while the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! m } will change. This is because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J^2} commutes with every component of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J} , (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_x} ,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_y} ,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_z} ), and therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J^2} commutes with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\vec \alpha}} . Indeed
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J^2 R_{\vec \alpha}|jm \rangle = \bold R_{\vec \alpha} J^2 |jm \rangle = j(j+1)R_{\vec \alpha}|jm \rangle}
Therefore, when we act with the rotation operator on a state, we are only mixing the multiplet. For example, acting on a 3d state with the rotation operator will result in a mixture of only the five 3d states. There will be no mixing of the 3p or 3s states.
Considering Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_z} , we know Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_z} will not commute with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold R_{\vec \alpha} } because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_z} does not commute with either Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_x} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J_y} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lbrack\bold J_z, \bold R_{\vec \alpha}\rbrack \ne0}
Therefore the rotated state can be expressed as a linear combination of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |jm'' \rangle} as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\vec \alpha}|jm \rangle= \sum _{m''=-j} ^{j}|jm'' \rangle d_{m''m} ^{(j)}(\vec \alpha)}
Multiplying this equation on the left by a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle jm'|} , and using the orthonormality of the angular momentum eigenstates we find
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{m'm} ^{(j)}(\vec \alpha) = \langle jm'|e^{-i \bold J \vec \alpha}|jm \rangle }
Thus we can associate with each rotation a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2J+1} by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2J+1} dimension matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold d_{\vec \alpha} ^{(j)}} whose matrix elements are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{m'm} ^{(j)}(\vec \alpha)} . These matrix elements don't depend on dynamics of the system; they are determined entirely by the properties of the angular momentum.
The matrices have a very important property. Two rotations performed in a row, say Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec \alpha} followed by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec \beta} , are equivalent to a single rotation, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec \gamma} . Thus
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\vec \gamma}=R_{\vec \beta}R_{\vec \alpha}}
Taking matrix elements of both sides and putting in a complete set of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j'm'\rangle} states between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\vec \beta}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\vec \alpha}} we find
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle jm|R_{\vec \gamma}| jm'\rangle=\sum_{m''}\langle jm|R_{\vec \beta}| jm''\rangle \langle jm''|R_{\vec \alpha}| jm'\rangle} ,
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{mm'} ^{(j)}(\vec \gamma)=\sum_{m''}d_{mm''} ^{(j)}(\vec \beta)d_{m''m'} ^{(j)}(\vec \alpha)}
or equivalently
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d ^{(j)}(\vec \gamma)=d ^{(j)}(\vec \beta)d ^{(j)}(\vec \alpha)}
A set of matrices associated with rotations having this property is call a representation of the rotation group.
The rotation operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\vec \alpha}} act on the set of states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |jm \rangle} for fixed j, in an irreducible fashion. To see what this means, let's consider the effect of rotations on the set of eight states for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=2} . Under any rotation a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=1} state becomes a linear combination of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=1} states, with no Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=2} components, conversely a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=2} state becomes a linear combination of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=2} states with no Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=1} components. Thus this set of eight states which transform each among themselves under rotation with no mixing. One says that the rotations act on these eight states reducibly. On the other hand, for a set of states all with the same j, there is no smaller subset of states that transforms privately among itself under all rotations; the rotations are said to act irreducibly. Put another way, if we start with any state, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |jm \rangle} , then we can rotate it Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2j+1} linearly independent states, and therefore there can't be any subspace of j states that transforms among itself under rotations. One can prove this in detail starting from the fact that one can generate all the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |jm \rangle} states starting form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |jj \rangle} by applying Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{-}} enough times.
Tensor operators
The types of operators having simple transform properties under rotations are known as tensor operators. By an irreducible tensor operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold T^{(k)}} of order k we shall mean a set of 2k+1 operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_q ^{(k)},\;q=\;-k,\;-k+1,....,k-1,\;k } that transform among themselves under rotation according to the transformation law:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\vec \alpha} T_q ^{(k)}R_{\vec \alpha} ^{-1}=\sum_{q'=-k}^{k}T_{q'} ^{(k)}d_{q'q}^{(k)}(\vec \alpha)}
If we consider and infinitesimal rotation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec \epsilon} ,then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\vec \epsilon } = e^{- \frac {i} {\hbar} \vec J \vec \epsilon} \approx 1- \frac {i} {\hbar} \vec J \vec \epsilon}
to the first order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \epsilon}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_q ^{(k)}-\frac {i}{\hbar}[\vec J \vec \epsilon , T_q ^{(k)}]=T_q ^{(k)}- \frac {i}{\hbar} \vec \epsilon \sum_{q'=-k}^{k}T_{q'} ^{(k)} \langle kq' |\vec J| kq \rangle}
Comparing coefficients of we see that tensor operators must obey the commutation relation with the angular momentum:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\vec J , T_q ^{(k)}]=\sum_{q'=-k}^{k}T_{q'} ^{(k)} \langle kq' |\vec J| kq \rangle}
The z component of this relation is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [J _z, T_q ^{(k)}]=qT_{q} ^{(k)}}
while
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [J _{\pm}, T_q ^{(k)}]=\sum_{q'=-k}^{k}T_{q'} ^{(k)}\langle kq' |J_{\pm}| kq \rangle=T_{q \pm 1} ^{(k)} \sqrt {k(k+1)-q(q \pm 1)}}
Tensor operators have many simple properties. For example, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_q ^{(k)}} acts on state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha j_1 m_1 \rangle} of a system (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \alpha} refers to other quantum number), creating a state whose z component of angular momentum is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q+m_{1}} . To prove this, let us consider the transformation properties of the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_q ^{(k)}|\alpha j_1 m_1 \rangle} under rotation about the z axis by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \phi}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\bold \phi}T_q ^{(k)}|\alpha j_1 m_1 \rangle = R_{\bold \phi}T_q ^{(k)}R_{\bold \phi}^{-1}R_{\bold \phi}|\alpha j_1 m_1 \rangle = \sum_{q'} T_{q'} ^{(k)} d_{q'q}^{(k)} \sum_{m'_{1}}|\alpha j_1 m'_1 \rangle d_{m'_1 m_1}^{(j_1)}(\bold \phi)}
but Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{m' m}^{(j)}(\bold \phi)=\delta _{m'm} e^{-im \bold \phi}}
so that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{\bold \phi}T_q ^{(k)}|\alpha j_1 m_1 \rangle = e^{-i(q+m_1)\bold \phi}T_q ^{(k)}|\alpha j_1 m_1 \rangle}
This is exactly the transformation law for an eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_z} with eigenvalue Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q+m_1} . Thus is an operator that increases the eigenvalue Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_z} of by q.
Wigner-Eckart theorem
The Wigner-Eckart theorem postulates that in a total angular momentum basis, the matrix element of a tensor operator can be expressed as the product of a factor that is independent of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{j_z}} and a Clebsch-Gordan coefficient. To see how this is derived, we can start with the matrix element Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \underbrace{\alpha \prime} j\prime m\prime |\underbrace{\tilde{\alpha}} j m\rangle} , where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \underbrace{\alpha}} represents all the properties of the state not related to angular momentum:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \underbrace{\alpha \prime} j\prime m\prime |\underbrace{\tilde{\alpha}} j m\rangle = \int d\alpha \langle \underbrace{\alpha \prime} j\prime m\prime |R_{\alpha}^{-1}R_{\alpha}|\underbrace{\tilde{\alpha}} j m\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \langle \underbrace{\alpha \prime} j\prime m\prime |\underbrace{\tilde{\alpha}} j m\rangle = \sum_{m_1 ,m_1 \prime} \int d\alpha \ d_{m_1 \prime m\prime}^{(j\prime )}(\alpha)^{*} d_{m_1 m}^{(j)}(\alpha)\langle \underbrace{\alpha \prime} j\prime m_1 \prime |\underbrace{\tilde{\alpha}} j m_1 \rangle}
Using the orthogonality of rotation matrices, this reduces to
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \underbrace{\alpha \prime} j\prime m\prime |\underbrace{\tilde{\alpha}} j m\rangle = \delta _{jj\prime} \delta _{mm\prime} \sum _{m_1} \frac{\langle \underbrace{\alpha \prime} j\prime m_1|\underbrace{\tilde{\alpha}} j\prime m_1 \rangle}{2j\prime +1}}
Finally, using the fact that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\underbrace{\tilde{\alpha}} j m\rangle = \sum_{q, \tilde{m}} T_{q}^{(k)}|\underbrace{\alpha} \tilde{j} \tilde{m}\rangle\langle k\tilde{j}q\tilde{m}|k\tilde{j}jm\rangle} and the orthogonality of the Clebsch-Gordan coefficients, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \underbrace{\alpha \prime} j\prime m\prime |T_{q}^{(k)}|\underbrace{\alpha} j m\rangle = \sum_{m_1}\frac{\langle \underbrace{\alpha \prime} j\prime m_1 |\underbrace{\tilde{\alpha}} j\prime m_1 \rangle}{2j\prime +1} \langle kjqm|kjj\prime m\prime \rangle }
Historically, this is written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \underbrace{\alpha \prime} j\prime m\prime |T_{q}^{(k)}|\underbrace{\alpha} j m\rangle = \frac{\langle \underbrace{\alpha \prime} j\prime || T_{q}^{(k)}|| \underbrace{\alpha} j \rangle}{\sqrt{2j\prime +1}} \langle kqjm|kjj\prime m\prime \rangle }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \underbrace{\alpha \prime} j\prime || T_{q}^{(k)}|| \underbrace{\alpha} j \rangle} is referred to as the reduced matrix element.
In summary, the Wigner-Eckart theorem states that the matrix elements of spherical tensor operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_q^{(k)}} with respect to the total-Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold J} eigenstates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j,m \rangle } can be written in terms of the Clebsch-Gordan coefficients, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <kq;jm|j\prime m\prime;kj\rangle} , and the reduced matrix elements of , which do not depend on the orientation of the system is space, i.e., no dependence on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! m\prime } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! m } , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \! q } : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \underbrace{\alpha \prime} j\prime m\prime |T_{q}^{(k)}|\underbrace{\alpha} j m\rangle = \frac{\langle \underbrace{\alpha \prime} j\prime || T_{q}^{(k)}|| \underbrace{\alpha} j \rangle}{\sqrt{2j\prime +1}} \langle kqjm|kjj\prime m\prime \rangle }
As an example of how this theory can be useful, consider the example of the matrix element Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{0}^{(1)} = z =r\cos \left(\theta \right)} with hydrogen atom states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n \ell m\rangle} . Because of the Clebsch-Gordan coefficients, the matrix element Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n\prime \ell \prime m\prime | T_{0}^{(1)}|n\ell m\rangle} is automatically zero unless Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{m=m\prime}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{\ell \prime = \ell \pm 1}} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{\ell}} . Also, because z is odd under parity, we can also eliminate the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell \prime = \ell} transition.
Also, for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\frac{1}{\sqrt{2}}\left(T_{-1}^{1}-T_{1}^{1}\right)} , the Wigner-Eckart Theorem reads
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n \ell m | x|n\ell m\rangle=\frac{1}{\sqrt{2}}\langle n \ell || T^1 || n \ell \rangle\left(C^{\ell m}_{\ell m11}-C^{\ell m}_{\ell m1-1}\right)}
The result vanishes since the CG coefficients on the right hand side are zero.
Problem [4]
EXAMPLE PROBLEM [5]
Application [6]
Elements of relativistic quantum mechanics
The description of phenomena at high energies requires the investigation of the relativistic wave equations, the equations which are invariant under Lorentz transformations. The translation from a nonrelativistic to a relativistic description, implies that several concepts of the nonrelativistic theory have to be reinvestigated, in particular:
(1) Spatial and temporal coordinates have to be treated equally within the theory.
(2) Since, from the Uncertainty principle, we know
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle x \sim \frac{\hbar}{\triangle p} \sim \frac{\hbar}{m_{0} c}} ,
a relativistic particle can not be localized more accurately than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx \hbar/{m_{0} c}} ; otherwise pair creation occurs for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E > 2m_{0} c^2} . Thus, the idea of a free particle only makes sense if the particle is not confined by external constraints to a volume which is smaller than approximately than the Compton wavelength Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_c=\hbar/{m_{0} c}} . Otherwise, the particle automatically has companions due to particle-antiparticle creation.
(3) If the position of the particle is uncertain, i.e. if
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle x > \frac{\hbar}{m_{0} c}} ,
then the time is also uncertain, because
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle t \sim \frac{\triangle x}{c} > \frac{\hbar}{m_{0} c^2}} .
In a nonrelativistic theory, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangle t} can be arbitrary small, because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c \to \infty} . Thereby, we recognize the necessity to reconsider the concept of probability density, which describes the probability of finding a particle at a definite place Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} at a fixed time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} .
(4) At high energies i.e. in the relativistic regime, pair creation and annihilation processes occur, ususlly in the form of creating particle-antiparticle pairs. Thus, at relativistic energies, particle conservation is no longer a valid assumption. A relativistic theory must be able to describe the phenomena like pair creation, vacuum polarization, particle conservation etc.
In nonrelativistic quantum mechanics, states of particles are described by Schrodinger equation of states:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial\psi(\bold r, t)}{\partial t}=\left(-\frac{\hbar^2}{2m}\nabla^2+V(\bold r, t)\right)\psi(\bold r, t)}
Schrodinger equation is a first order differential equation in time. However, it is second order in space and therefore, it is not invariant under the Lorentz transformations. As mentioned above, in relativistic quantum mechanics, the equation describing the states must be invariant under the Lorentz transformations. In order to satisfy this condition, equation of state must contain the derivatives with respect to time and space of the same order. Equations of states in relativistic quantum mechanics are Klein-Gordon equation (for spinless particles) and Dirac equation (for spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {1}{2}} particles). The former contains second ordered derivatives while the latter contains first ordered derivatives with respect to both time and space. The way to derive these equations is similar to that of Schrodinger equation: making use of the correspondence principle, starting from the equation connecting the energy and momentum with the substitution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \frac {\partial}{\partial t}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold p} by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -i\hbar \nabla} .
Follow this link to learn about Klein-Gordon equation.
Follow this link to learn about Dirac equation.
Here is a worked problem for a free relativistic particle.
Here is a worked problem to review the use of relativistic 4-vectors: relativistic 4-vectors
The Adiabatic Approximation and Berry Phase
The adiabatic approximation can be applied to systems in which the Hamiltonian evolves slowly with time. The Hamiltonian of an adiabatic system contains several degrees of freedom. The basic idea behind the adiabatic approximation is to solve the Schrodinger equation for the "fast" degree of freedom and only then allow the "slow" degree of freedom to evolve slowly. For example, imagine a molecule with a heavy nucleus and an electron. In this system there is a "slow" degree of freedom (the nucleus) and a "fast" degree of freedom (the electrons). Imagine that the nucleus is stationary, and the electrons align themselves. Now that the electrons have aligned themselves, allow the nucleus to move very slowly - which will cause the electrons to realign. This is the adiabatic approximation.
Adiabatic Process
The gradual change in the external conditions characterizes an adiabatic process. In another word, let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{i}} be the internal characteristic frequency, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{e}} be the external characteristic frequency. The adiabatic process is one for which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{e}>>T_{i}} .
The Adiabatic Theorem
The adiabatic theorem states that if a system is initially in the nth state and if its Hamiltonian evolves slowly with time, it will be found at a later time in the nth state of the new Hamiltonian. (Proof: Messiah Q.M. (wiley NY 1962) Vol II ch. XVII)
Application(Born-Oppenheimer Approximation)[7]
Geometric Phase (Berry Phase)
The phase of a wave function is often considered arbitrary, and it is canceled out for most physics quantities, such as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi |^2 } . For that reason, the time-dependent phase factor on the wave function of a particle going from the nth eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}_0} to the nth eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}_t} was ignored. However, Berry showed that if the Hamiltonian is evolved over a closed loop the relative phase is not arbitrary, and cannot be gauged away. For more information on this discovery, see this paper. This is called the Berry Phase.
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x, 0) = |n (0)\rangle} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (x,t)\simeq e^{\theta _n(t)}e^{\gamma (t)}|n(t)\rangle} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta _n(t)=-\frac{1}{\hbar }\int _{\text{t0}}^tE_n\left(t'\right)dt'} , is called dynamic phase, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma (t)} is geometric phase.
Do you want to know what geometric phase looks like? If so, let' s begin our work :
Substitute Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left.\psi (x,t)\simeq e^{\theta _n(t)}e^{\gamma (t)}\right|n(t)\rangle} into Schrodinger equation,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \left[\frac{\partial }{\partial t}\left|n(t)\rangle e^{i\theta (t)}e^{i\gamma (t)}-\frac{i}{\hbar }E_n(t)\right|n(t)\rangle e^{i\theta (t)}e^{i\gamma(t)}+i\frac{d\gamma _n(t)}{dt}|n(t)\rangle e^{i\theta(t)}e^{i\gamma(t)}\right]=H(t)|n(t)\rangle e^{i\theta(t)}e^{i\gamma (t)}=E_n(t)|n(t)\rangle e^{i\theta(t)}e^{i\gamma(t)}}
So, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\gamma _n(t)}{dt}=i\langle n(t)|\frac{\partial }{\partial t}|n(t)\rangle.}
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial }{\partial t}|n(t)\rangle=\frac{\partial |n(t)\rangle}{\partial R}\frac{\partial R}{\partial t}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore \gamma _n(t)=i\int _{t_0}^t\langle n\left(t'\right)|\frac{\partial }{\partial t}\left|n\left(t'\right)\rangle dt'\right.=i\int _{t_0}^t\langle n\left(t'\right)|\frac{\partial }{\partial R}\left|n\left(t'\right)\rangle\frac{\partial R}{\partial t'}dt'\right.=\int _{R_i}^{R_f}\langle n\left(t'\right)|\frac{\partial }{\partial R}\left|n\left(t'\right)\rangle dR\right.}
This is the expression of geometric phase.If it's a 1 D problem : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma _n(t)=0} , there is no geometric phase change.
If more than 1 D: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma _n(t)=\int _{R_i}^{R_f}\langle n\left(t'\right)|\nabla _R\left|n\left(t'\right)\rangle dR.\right.}
The larger number of dimensions allows for the geometric phase change.
Berry' s phase : If the Hamiltonian returns to its oringinal form after a time T, the net geometric phase change is :Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma _n(t)=\oint \langle n\left(t'\right)|\nabla _R\left|n\left(t'\right)\rangle dR.\right.}
Why geometric phase is special? Because it does have physical meaning. We can observe it from interference experiment.Berry Potentials
It is possible to construct potentials that give rise to this phase, by carefully considering a general Hamiltonian of two interacting particles, where one is much larger (and hence slower) than the other. (This can also be done for more particles, but the construction in very similar.)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = \frac{P^2}{2m_n} + \frac{p^2}{2m_e} + V(\vec{R},\vec{r}) } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{R}} refers to the coordinate of the larger particle, and not the center of mass.
After some work, it can be shown that terms similar to both a vector and scalar potential can be found that explicitly create the Berry Phase.
The final result is:
for the Vector Potential,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A^{(n)} = i\hbar \langle n(R)|\vec{\nabla_R}|n(R)\rangle }
and for the Scalar Potential,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi^{(n)} = \frac{\hbar^2}{2m_n}\left(\langle\vec{\nabla_R} n(R)|\vec{\nabla_R} n(R) \rangle - \langle \vec{\nabla_R} n(R)|n(R)\rangle \langle n(R)|\vec{\nabla_R}n(R)\rangle \right) }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n(R)\rangle } is the wavefunction of the smaller particle, depending on the position of the larger. More generally, it would be the wavefunction of the object with the 'fast' degree of freedom, depended on the state of the slower degree of freedom.
Once these are found, an effective Hamiltonian may be constructed:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = \frac{1}{2m_n}\left(\vec{P}-\vec{A^{(n)}}\right)^2 + \Phi^{(n)} }
Time Reversal Symmetry (& Kramer's Degeneracy)
The Schrodinger equation is: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial }{\partial (t)}\psi(r,t) =H\psi(r,t)}
Taking t Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow} -t yeilds: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -i\hbar\frac{\partial }{\partial (t)}\psi(r,-t) =H\psi(r,-t)}
This is obviously not a symmetric transformation. In addition, take the complex conjugate: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial }{\partial (-t)}\psi ^*=H^*\psi ^*}
Whether or not this equation is symmetric depends on the form of H we are working with.
To find an expression for the time reversal operator, we consider the specific Hamiltonian for an electron:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = \frac{p^2}{2m} + V(r) + (\frac{1}{2m^2c^2}\frac{1}{r}\frac{dV}{dr})\mathbf{L}\cdot \mathbf{S}}
The time reversal operator for a one electron system is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{K} = i \sigma _{y} C } where C indicates to take the complex conjugate
Prove:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K\psi=i\sigma_y\psi^*}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KHK^{\dagger}=(i\sigma_yC) H (-i\sigma _yC^*)=H^*}
To get degeneracy from the time reversal. (Kramers Degeneracy)
For n-electrons:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{K}=i^n\sigma _{y_1}\sigma _{y_2}...\sigma _{y_n}C}
For time reversal invariant H: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (KHK^{\dagger})K\psi=E(K\psi)}
So, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K\psi} have same energy.
Assume they are linear dependent: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K\psi=\psi^'=a\psi}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K^2\psi=K\psi^'=K\psi=a^*K\psi=a^*a\psi=\psi}
It requires Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K^2=1} .
However, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K^2=(i^n\sigma_y1\sigma_y2...\sigma_yn C)(i^n\sigma_y1\sigma_y2...\sigma_yn C)=(-1)^n}
And thus we have arrived at Kramer's Degeneracy Theoreom: For an odd number of electrons, the energy levels of the system are at least doubly degenerate, as long as H is time reversal invariant.
Many Particle Systems and Identical Particles
At this point it is second nature to write down the hamiltonian for a system if the potential and kinetic energy of the particle is known. The hamiltonian is then denoted by: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat H = \frac{p^2}{2m} + V(\vec r) }
The next natural step is to investigate what the hamiltonian would look like and the resulting wavefunctions and energies for systems with more than one particle. The easiest place to start is with two identical particles.
Two Identical Particles
It is straight forward to generalize a Hamiltonian for two identical particles:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat H = \frac{p_1^2}{2m} + \frac{p_2^2}{2m} + V(\vec r_1) + V(\vec r_2) + (u(\vec r_1, \vec r_2) + u(\vec r_2, \vec r_1)), }
where the potential and kinetic energy are written down for each particle individually and there is an additional term which represents the interaction between the two particles. For simplicity we will treat the interaction potential as a central force and from this point on write it as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(| \vec r_1 - \vec r_2|) } .
The above Hamiltonian for the two identical particles is invariant under exchange symmetry (or the permutation of particle labels) and as such it is either even or odd under permutation. Likewise the eigenfunctions can be chosen to be even or odd under the exchange of particle labels. Ignoring spin orbit coupling the general solution will therefore be of the form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (\eta_1, \eta_2) = \phi (\vec r_1, \vec r_2) \chi (\sigma_1, \sigma_2), }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_1 \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_2 \!} are just spin labels not Pauli spin matrices. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (\eta_1, \eta_2) \! } is a solution, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (\eta_2, \eta_1) \! } is also a solution and as such there are two possible states, one is symmetric and the other is anti-symmetric solution:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{1}{\sqrt{2}} \left(\psi (\eta_1, \eta_2) + \psi (\eta_2, \eta_1)\right) }
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{1}{\sqrt{2}} \left(\psi (\eta_1, \eta_2) - \psi (\eta_2, \eta_1)\right) }
Although mathematically this formula will result in symmetric and anti-symmetric solutions, in nature that is not the case, and the solution must be chosen to be one or the other. If the system deals with two fermions, which have half-integer spin, then only the anti-symmetric solution appears in nature. Likewise if the system deals with two bosons, which have integer spin, then only the symmetric solution appears in nature.
N Particles
If the Hamiltonian were for a three particle system, it would be:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat H = \frac{p_1^2}{2m} + \frac{p_2^2}{2m} + \frac{p_3^2}{2m} + V(\vec r_1) + V(\vec r_2) + V(\vec r_3) +(u(|\vec r_1 - \vec r_2 |) + u(| \vec r_1 - \vec r_3 |) + u(| \vec r_2 - \vec r_3 |).}
In general, the Hamiltonian for a system with N particles can be written as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat H = \sum _{j=1} ^{N} \left( \frac{p^2_j}{2m} + V(\vec r_j)\right) + \frac{1}{2} \sum_{j,k}^N u(r_j, r_k). }
In general, it is difficult to solve this problem with interaction terms but assuming you could do so. The only physically admissible states are either symmetric or antisymmetric under exchange of any two particle labels as before, therefore, the wavefunction is given by: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (\eta_1, \eta_2, \eta_3, ... , \eta_N) = \phi (\vec r_1, \vec r_2, \vec r_3, ... , \vec r_N) \chi (\sigma_1, \sigma_2, \sigma_3, ..., \sigma_N) } ,
and it follows the same rules as before for bosons and fermions.
It is important to note that if a solution doesn't satisfy the proper symmetry, then a linear combination of all permutations will result in a properly symmetrized solution that will be an eigenstate.
Constructing Admissible Eigenstates
As stated above, if a solution does not satisfy the necessary symmetry properties, then a linear combination of the different permutations of product states (that are completely symmetric for bosons and anti-symmetric for fermions) must be made.
For spin-less bosons the normalized wavefunction is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{\mbox{bosons}} (1,2,....N) = \sqrt{\frac{N_a! N_b! .... N_n!}{N!}} \sum_P P \varphi_a (1) \varphi_b(2) ....... \varphi_n (N)}
where the sum is over all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N!\!} permutations of indices 1 through Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N \!} .
For spin-less fermions the normalized wavefunction is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{\mbox{fermions}} (1,2,....N) = \frac{1}{\sqrt{N!}}\sum_P (-1)^P P \varphi_a (1) \varphi_b(2) ....... \varphi_n (N)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1)^P \!} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +1 \!} if a permutation can be decomposed into an even number of two particle exchanges and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 \!} for odd.
Another way of writing the sum to form an anti-symmetric matrix is through the use of the Slater determinant.
Second Quantization
Consider now a wavefunction pertaining to a many-particle system, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (\eta_1, \eta_2, \eta_3, ... , \eta_N) \!} , which is considered to be a field variable. For the many-particle system, this field variable must also quantized by a process known as second quantization.
In order to perform this quantization of the field variable, we must construct special raising and lowering operators, associated with the individual energy levels of the system, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}_j ^{\dagger} \!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}_j \!} , which add and subtract particles from the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^{th} \!} energy level, respectively. In the presence of spin, an additional subscript is added to separate the creation and annihilation operators for each case of spin, so that each operator only acts on particles with the same spin attributed to said operator. In the simple, although rather non-physical, case of spinless particles, this extra factor can be ignored for simplicity in examining how the operators work on the quantized field:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}_j ^{\dagger} |0\rangle = |1\rangle \!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}_j |1\rangle = |0\rangle \!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}_j |0\rangle = 0 \!}
For the case of fermions, an additional constraint on the operators is placed due to the exclusion principle: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a} ^{\dagger} |1\rangle = 0 \!}
Given the two classes of particles, fermions and bosons, two sets of relations result to relate the creation and annihilation operators.
For the case of bosons, the operators obey a commutator relationship of the form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\hat{a}_i, \hat{a}_j ^{\dagger}] = \delta_{ij}; [\hat{a}_i, \hat{a}_j] = [\hat{a}_i ^{\dagger}, \hat{a}_j ^{\dagger}] = 0 \!}
The state of the system, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_0, n_1, .., n_N\rangle \!} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_j \!} refers to the number of particles in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^{th} \!} state, is therefore of the form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_0, n_1, .., n_N\rangle = {\frac{(\hat{a}_0 ^{\dagger})^{n_o}}{\sqrt{n_0 !}}}{\frac{(\hat{a}_1 ^{\dagger})^{n_1}}{\sqrt{n_1 !}}}...{\frac{(\hat{a}_N ^{\dagger})^{n_N}}{\sqrt{n_N !}}} |0\rangle \!}
Fermions, however, obey anti-commutator relationships, of the following form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ \hat{a}_i, \hat{a}_j ^{\dagger} \} = \delta_{ij}; \{ \hat{a}_i, \hat{a}_j \} = \{ \hat{a}_i ^{\dagger}, \hat{a}_j ^{\dagger} \} = 0 \!}
For this type of system, the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_0, n_1, .., n_N\rangle \!} can be written as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_0, n_1, .., n_N\rangle = (\hat{a}_0 ^{\dagger})^{n_0}(\hat{a}_1 ^{\dagger})^{n_1}...(\hat{a}_N ^{\dagger})^{n_N} |0\rangle \!}
Furthermore, for both classes of particles, we can create an operator that, upon acting on the total state of the system, returns the number of particles in a given Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{th} \!} state (for fermions this will obviously be 0 or 1). This operator is of the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}_n ^{\dagger} \hat{a}_n \!} . Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}_j ^{\dagger} \hat{a}_j |n_0, n_1, .., n_N\rangle = n_j |n_0, n_1, .., n_N\rangle \!} . From this it is easy to obtain an operator, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{N} \!} that returns the total number of particles in the system:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{N} = \sum_{j=0}^{\infty} \hat{a}_n ^{\dagger} \hat{a}_n \!}
From this operator, the average number of particles, and therefore the average flux number, can be calculated by the following:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \Psi | \hat{N} | \Psi\rangle = \langle \hat{N} \rangle \!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \Psi | {\langle \hat{N} - {\langle \hat{N} \rangle} \rangle}^2 | \Psi\rangle = \langle \hat{N}^2 \rangle - {\langle \hat{N} \rangle}^2 \!}
To continue the analysis of these second quantization operators, lets consider the projection of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a} ^{\dagger} \!} on the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0\rangle \!} , that is to say, define a function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_j(\mathbf r) \!} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \mathbf{r} | \hat{a}_j ^{\dagger} |0\rangle = \phi_j(\mathbf r) \!}
Rearranging this yields an expression for the position state of a particular particle, weighted over the different energy levels by the function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_j(\mathbf r) \!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\mathbf{r}\rangle = \sum_{j=0}^{\infty} \phi_j^*(\mathbf r)\hat{a}_j ^{\dagger} |0\rangle \!}
This new field operator acting on the ground state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0\rangle \!} is called the field creation operator:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi ^{\dagger}(\mathbf r) \equiv \sum_{i=0}^{\infty} \phi_i^*(\mathbf r) \hat{a}_i ^{\dagger} \!}
Therefore, the position state of a system containing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n\!} particles can be expressed as the following:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\mathbf{r}_1, \mathbf{r}_2, .., \mathbf{r}_n\rangle = {\frac{1}{\sqrt{n!}}}\Psi ^{\dagger}(\mathbf{r}_n)...\Psi ^{\dagger}(\mathbf{r}_2)\Psi ^{\dagger}(\mathbf{r}_1)|0\rangle\!}
Here it is important to note the permutation relationships differ for fermions and bosons, that is to say the following:
For bosons: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\mathbf{r}_1, \mathbf{r}_2, .., \mathbf{r}_n\rangle = |\mathbf{r}_2, \mathbf{r}_1, .., \mathbf{r}_n\rangle \!}
Whereas for fermions: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\mathbf{r}_1, \mathbf{r}_2, .., \mathbf{r}_n\rangle = -|\mathbf{r}_2, \mathbf{r}_1, .., \mathbf{r}_n\rangle \!}
Manipulation of the field creation and annihilation operators yield results congruent with those associated with the particle creation and annihilation operators discussed above, recognizing that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_j \phi_j(\mathbf r)\phi_j^*(\mathbf{r'}) \!} is a delta function. Therefore, we obtain the following expressions:
For fermions, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ \Psi(\mathbf r), \Psi^{\dagger}(\mathbf r') \} = \delta(\mathbf{r - r'}); \{ \Psi(\mathbf r), \Psi(\mathbf r') \} = \{\Psi^{\dagger}(\mathbf r), \Psi^{\dagger}(\mathbf r') \}= 0 \!}
And for bosons, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [ \Psi(\mathbf r), \Psi^{\dagger}(\mathbf r') ] = \delta(\mathbf{r - r'}); [ \Psi(\mathbf r), \Psi(\mathbf r') ] = [\Psi^{\dagger}(\mathbf r), \Psi^{\dagger}(\mathbf r') ]= 0 \!}
From these relations, we show that adding a particle at position Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r} \!} is expressed by the automatically correctly symmetrized expression:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi^{\dagger}(\mathbf{r}) |\mathbf{r}_1, \mathbf{r}_2, .., \mathbf{r}_n\rangle = \sqrt{n+1}|\mathbf{r}_1, \mathbf{r}_2, .., \mathbf{r}_n, \mathbf{r}\rangle \!}
The annihilation operator also results in a correctly symmetrized expression, however, it is only valid if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r} \in \{ \mathbf{r}_1, \mathbf{r}_2, .., \mathbf{r}_n\} \!} . The result is a correctly symmetrized combination of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n - 1\!} particle states:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(\mathbf{r})|\mathbf{r}_1, .., \mathbf{r}_n\rangle = \frac{1}{\sqrt{n}}(\delta(\mathbf{r} - \mathbf{r}_n)|\mathbf{r}_1, .., \mathbf{r}_{n-1}\rangle \pm \delta(\mathbf{r} - \mathbf{r}_{n-1})|\mathbf{r}_1, ..,\mathbf{r}_{n-2}, \mathbf{r}_n\rangle + \delta(\mathbf{r} - \mathbf{r}_{n-2})|\mathbf{r}_1, ..,\mathbf{r}_{n-3}, \mathbf{r}_{n-1}, \mathbf{r}_n\rangle \pm ... (\pm 1)^{n-1}\delta(\mathbf{r} - \mathbf{r}_1)|\mathbf{r}_2, ..,\mathbf{r}_n\rangle) \!}
Finally, we will consider certain preexisting operators, expressed in the new second quantization format. Consider first the density operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\rho}(\mathbf r) \!} which was previously Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{j=1}^N \delta(\mathbf{r} - \mathbf{r}_j) \!} in the first quantization. Recalling our earlier commutator relations, this operator is refined as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\rho} = \Psi^{\dagger}(\mathbf{r})\Psi(\mathbf{r}) \!}
In order to obtain the total kinetic energy and interaction potential operators, one must first express the annihilation and creation operators in momentum space to simplify the mathematics. Therefore, define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(\mathbf{r}) = \sum_{\mathbf{p}} \frac{e^\frac{i\mathbf{p}\cdot\mathbf{r}}{ \hbar}}{\sqrt{V}}\hat{a}_p \!} . Therefore, rearranging this yields:
Therefore, for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{T} = \sum_{\mathbf{p}} \frac{{\mathbf{p}}^2}{2m} \hat{a}^{\dagger}_{\mathbf{p}} \hat{a}_{\mathbf{p}} \!} , we can rewrite this as the following:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{T} = \frac{{\hbar}^2}{2m}\int d^3 \mathbf{r}( \mathbf{\nabla}\Psi^{\dagger}(\mathbf{r}))\cdot(\mathbf{\nabla}\Psi(\mathbf{r})) \!}
The interaction potential, taking care to include the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}\!} term for symmetry, is thereby expressed as:
Note that this entire analysis has been done for the spinless particle case, however the addition of spin only requires that we sum over the possible spins of the system, namely:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{T} = \frac{{\hbar}^2}{2m}\sum_s\int d^3 \mathbf{r}( \mathbf{\nabla}\Psi_s^{\dagger}(\mathbf{r}))\cdot(\mathbf{\nabla}\Psi_s(\mathbf{r})) \!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{V} = \frac{1}{2}\sum_{s, s'}\int d^3 \mathbf{r} d^3 \mathbf{r'} V(\mathbf{r} - \mathbf {r'}) \Psi_s^{\dagger}(\mathbf{r}) \Psi_{s'}^{\dagger}(\mathbf{r'}) \Psi_{s'}(\mathbf{r'}) \Psi_s (\mathbf{r}) \!}
Thus finally the total Hamiltonian for the system can be written as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H} = \hat{T} + \hat{V} = \frac{{\hbar}^2}{2m}\sum_s\int d^3 \mathbf{r}( \mathbf{\nabla}\Psi_s^{\dagger}(\mathbf{r}))\cdot(\mathbf{\nabla}\Psi_s(\mathbf{r})) + \frac{1}{2}\sum_{s, s'}\int d^3 \mathbf{r} d^3 \mathbf{r'} V(\mathbf{r} - \mathbf {r'}) \Psi_s^{\dagger}(\mathbf{r}) \Psi_{s'}^{\dagger}(\mathbf{r'}) \Psi_{s'}(\mathbf{r'}) \Psi_s (\mathbf{r}) \!}
relativistic Quantum mechanics and Dirac Equation
- If we see a circular polarized light then by conservation of angular momentum we know that









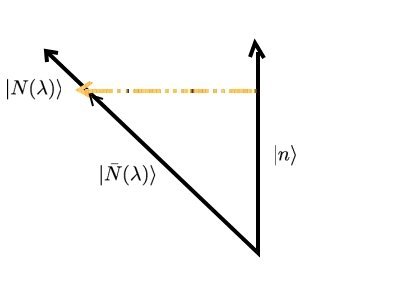








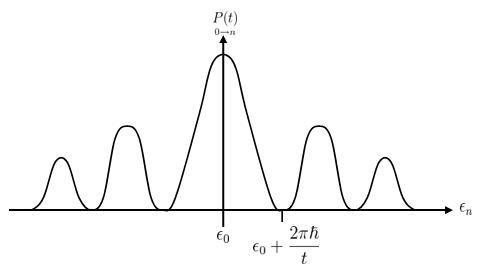




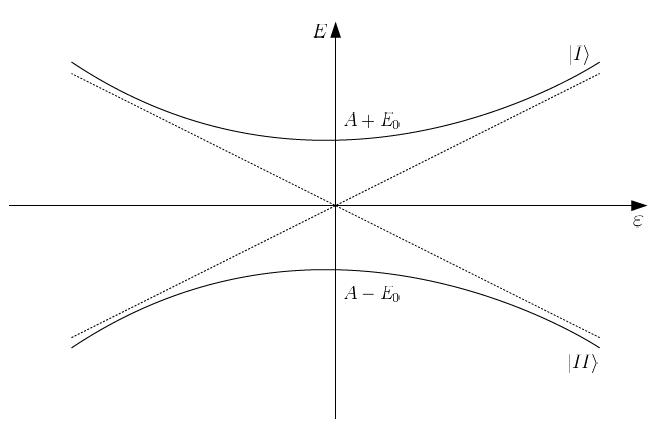
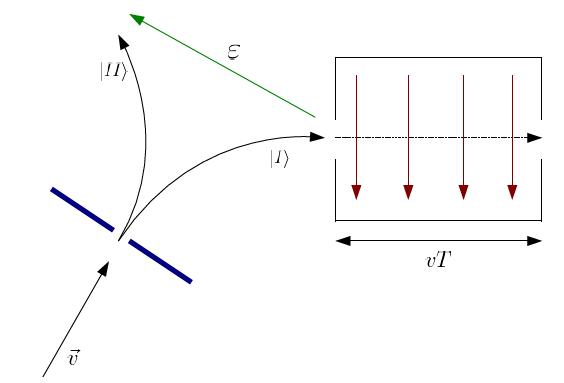







![{\displaystyle {\begin{aligned}{\mathcal {H}}&={\mathcal {H}}_{0}+\sum _{i=1}^{N}-{\frac {e}{2mc}}\left({\vec {p}}_{i}\cdot \int d^{3}{r}\;\delta ({\vec {r}}-{\vec {r}}_{i}){\vec {A}}({\vec {r}},t)+\int d^{3}{r}\;\delta ({\vec {r}}-{\vec {r}}_{i}){\vec {A}}({\vec {r}},t)\cdot {\vec {p}}_{i}\right)\\&\;\;\;\;\;\;\;\;\;+\sum _{i=1}^{N}{\frac {e^{2}}{2mc^{2}}}\int d^{3}{r}\;\delta ({\vec {r}}-{\vec {r}}_{i})A({\vec {r}},t)^{2}+e\sum _{i=1}^{N}\int d^{3}{r}\;\delta ({\vec {r}}-{\vec {r}}_{i})\phi ({\vec {r}},t)\\&={\mathcal {H}}_{0}-\int d^{3}{r}\;{\frac {e}{c}}\underbrace {\left[{\frac {1}{2}}\sum _{i=1}^{N}\left[{\frac {{\vec {p}}_{i}}{m}}\delta ({\vec {r}}-{\vec {r}}_{i})+\delta ({\vec {r}}-{\vec {r}}_{i}){\frac {{\vec {p}}_{i}}{m}}\right]\right]} _{{\vec {j}}({\vec {r}})}{\vec {A}}({\vec {r}},t)\\&\;\;\;\;\;\;\;\;\;+\int d^{3}{r}\;{\frac {e^{2}}{2mc^{2}}}\underbrace {\left[\sum _{i=1}^{N}\ \delta ({\vec {r}}-{\vec {r}}_{i})\right]} _{\rho ({\vec {r}})}A({\vec {r}},t)^{2}+e\int d^{3}{r}\;\underbrace {\left[\sum _{i=1}^{N}\delta ({\vec {r}}-{\vec {r}}_{i})\right]} _{\rho ({\vec {r}})}\phi ({\vec {r}},t)\\&={\mathcal {H}}_{0}+\underbrace {\int d^{3}{r}\;\left[-{\frac {e}{c}}{\vec {j}}({\vec {r}})\cdot {\vec {A}}({\vec {r}},t)+{\frac {e^{2}}{2mc^{2}}}\rho ({\vec {r}})A({\vec {r}},t)^{2}+e\rho ({\vec {r}})\phi ({\vec {r}},t)\right]} _{{\mathcal {H}}_{int}}\\&={\mathcal {H}}_{0}+{\mathcal {H}}_{int}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a05b9715b4c94a8b43bcbde150c222e3abbe237b)