2nd Week: Properties of Astrophysical Plasmas B

Before an in-depth analysis of nuclear astrophysics can begin, one must review the basics of nuclear physics. This begins with thermodynamics.

Astrophysical Plasmas

The properties of astrophysical plasmas include

Thermodynamics for Quantum systems

Distrubution Functions

Thermodynamical Variables and Potentials

General and limiting Equation of State

Basics of Thermodynamics

Here are the definitions of some of the basic quantities.

The particle density: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \int_{0}^{\infty}{\omega(p)f(p)dp}}

The energy density: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = \int_{0}^{\infty}{E\omega(p)f(p)dp}}

The pressure: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = {1\over3} \int_{0}^{\infty}{pv\omega(p)f(p)dp}}

where v is the velocity, p is the momentum, E is the energy, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p)} is the probability function, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(p)} is the state density.

Other important Thermodynamical variables are:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dQ=TdS}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dU=TdS-PdV+\mu dN}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dS={1\over T}dU+{P\over T}dV-{\mu \over T}dN}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dF=-SdT-PdV+\mu dN}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dH=TdS+VdP+\mu dN}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dG=-SdT+VdP+\mu dN}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\Omega=-SdT-PdV-N\mu}

Where Q, U, S, F, H, and G are the heat, energy, entropy, free energy, enthalpy, and free enthalpy respectively.

Wave State Derivation

A brief derivation of a wave state density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(E)} .

One can begin with the stationary Schroedinger equation.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H \psi_{1,2,...n} = \left(T + V\right) \psi_{1,2,...n} = E \psi_{1,2,...n} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = \sum_{i=1}^{n}t_i = \sum_{i=1}^{n} -{\hbar^2\over2m}\nabla_{i}^2}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = \sum_{i=1}^{n}\sum_{j>i}^{n} v_{ij}}

However, for noninteracting particles: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t\left(i,j\right) = v\left(i,j\right) = 0}

The free particle case

Assuming that H describes a particle in a box of size d. So then breaking Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} into Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_x\psi_y\psi_z} one gets the solution:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_x = \sqrt{2\over d} sin\left({\sqrt{2mE}\over \hbar}x\right)} and that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\sqrt{2mE}\over \hbar} = n_x\pi}

This has a corresponding energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_x = {\pi^2\hbar^2 \over 2md^2} n_{x}^2}

One will get similar solutions for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_y} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_z} .

This means that the total energy of the particle can be found by: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{n_x n_y n_z} = {\pi^2\hbar^2 \over 2md^2} \left(n_{x}^2 + n_{y}^2 + n_{z}^2\right) = {\pi^2\hbar^2 \over 2md^2} R_{\rho}^2}

One does not want all of the eigenstates but only those within a certain range. These can be described as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(E) = {1 \over 8} {4\pi \over 3} R_{\rho}^3 = {4\pi \over 3} {V(2m)^{3/2} \over \hbar^3} E^{3/2}}

Then taking the derivative with respect to E and dividing by the volume will give the wave state density.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(E) = {1 \over V}{\partial \phi \over \partial E} = {2\pi(2m)^{3/2} \over \hbar^3} E^{1/2} }

Occupation probabilities

Maxwell-Boltzmann

The probability distribution can be found by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\epsilon_k) = \left( e^{ (\epsilon_k - \mu)/kT } \right)^{-1}}

Fermi-Dirac

Suppose that our system has discrete energies and that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_k} is the number of particles occupying the energy level Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k} . This two quantities must satisfy

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=\sum_{k}n_k }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{Total}=\sum_{k}n_k\epsilon}

Since we are dealing with fermions, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_k} can be 0 or 1. The thermodynamic (Landau) potential for a particular energy sate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k} can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_k=-kT \log (\sum_{n_k=0}^1 e^{n_k(\mu-\epsilon_k)/kT})}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_k=-kT \log (1 + e^{(\mu-\epsilon_k)/kT})}

Recall that, the mean particle number in a certain energy state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k} is minus the derivative of the thermodynamic potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_k} with respect to the chemical potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} . Therefore

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\epsilon_k)=-{\partial \Omega_k \over \partial \mu}= kT{e^{(\mu-\epsilon_k)/kT}\over kT(1+e^{(\mu-\epsilon_k)/kT})}}

Or simply as:

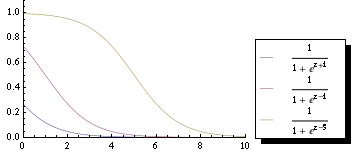
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\epsilon_k)={1 \over {e^{(\epsilon_k-\mu)/kT}+1}}}

Bose-Einstein

Consider a gas of bosons in which the particles satisfy the same two equations for N and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{Total}} . Similarly as in the Fermi-Dirac case, we can write the thermodynamic potential for a particular energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k} as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_k=-kT \log (\sum_{n_k=0}^\infty e^{n_k(\mu-\epsilon_k)/kT})}

In this case there is no restriction on the number of particles occupying the same state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k} . This is because the particles have integer spin, and therefore they are not limited by Pauli exclusion principle. Notice that the sum in the previous equation is convergent only if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\mu-\epsilon_k)<0 } . This condition must be satisfied for all the values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k} . If we choose Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k\geq 0} then we must have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu<0} . Therefore, in our particular energy scale, the chemical potential in a bosonic gas is always negative (although photons are an exception to this rule since the chemical potential for a photon gas is zero). Recall that for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\leq x<1}

$\sum _{n=0}^{\infty }x^{n}={1 \over {1-x}}$

Using this in the thermodynamic potential, with $x=e^{(\mu -\epsilon _{k})/kT}$ we get

$\Omega _{k}=-kT\log({1 \over {1-e^{(\mu -\epsilon _{k})/kT}}})=kT\log(1-e^{(\mu -\epsilon _{k})/kT})$

And as in the Fermi-Dirac case

$f(\epsilon _{k})=-{\partial \Omega _{k} \over \partial \mu }=kT{e^{(\mu -\epsilon _{k})/kT} \over kT(1-e^{(\mu -\epsilon _{k})/kT})}$

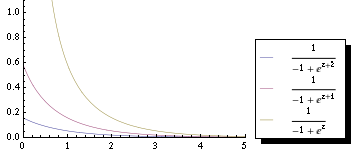
Or simply as:

$f(\epsilon _{k})={1 \over e^{(\epsilon _{k}-\mu )/kT}-1}$

A simple application: Existence of White Dwarfs, Neutron Stars and Black Holes

If we look into the interior of a star there is a upward force of pressure counteracting the downward force of gravity. If these two forces are not at equilibrium we see severe consequences for stellar structures such as the formation of degenerate stars.

Simple Estimates for Stellar Structure

The equation for pressure equilibrium is given by

${\frac {dP_{r}}{dr}}=-\rho _{r}{\frac {GM_{r}}{r^{2}}}$,

however as a rough estimate we can estimate it by the equation

dP= P(central)-P(surface)