3nd Week: Equation of State & Basic Properties of Nuclei
As we stated in the previous lectures, the nuclei of atom consists of nucleons: protons and neutrons. The most successful models that could describe the nucleus are the followings: Fermi gas model, Interacting boson model, Liquid drop model, Quark model and Shell model.
Equation of State
The equation that gives a relation among the thermodynamic variables, such as pressure, volume and temperature, is known as the equation of state. We already gave the general expressions for the particle density and pressure in the previous lecture, i.e. the particle density is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \frac{N}{V} =\int_{0}^{\infty }{w(p)f(p)dp} \ , }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p)} is the occupation probability and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w(p)} is the state density per unit volume. And the pressure for a given system is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{1}{3}\int_{0}^{\infty }{pvw(p)f(p)dp} \ , }
Herein we give the expressions for different type of gases: ideal Boltzmann gas, photon gas and non relativistic Fermi gas.
Ideal Boltzmann gas
In this model all the molecules in the gas are treated as non-interacting point particles engaged in random motion that obey the conservation of energy. The equation of state is easily obtained by substituting the occupation probability of Maxwell-Boltzmann distribution that leads to \
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = nk_BT \ . }
Photon gas
The calculation shows that in this case the equation of state is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{1}{3} \left(\frac{8 \pi^5 k^4}{15c^3 h^3}\right) T^4 \ . }
Non relativistic Fermi gas
The equation of state in this case is found as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = {2 \over 3} nkT {F_{3/2}\left(- {\mu \over KT}\right) \over F_{1/2}\left(- {\mu \over KT}\right)} \ .}
For non degenerate Fermi gas when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle kT<< \mu} , we regain the ideal Boltzmann gas.
Nuclear properties
The nucleus consists of protons and neutrons. Their mass are relatively close to each other
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_p=938.272 \ MeV/c^2 \ , }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_n=939.565 \ MeV/c^2 \ , }
and have the same spin equal to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar/2} . The proton has the positive charge with magnitude equal to that of electron, while the neutron, as its name states, is neutral. The force between nucleons are mainly the attractive strong force with a very short range (~ 1 fm). However due to the existence of the charge of proton there is also a repulsive electromagnetic force that acts between two protons. The approximate radius of the nucleus is defined by the following formula
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R = 1.3 \cdot A^{1/3} \ fm \ , }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is the atomic number.
Nuclear mass and binding energy
The total nuclear mass, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{nuc}} , is less than the sum of masses of the constituent nucleons and is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{nuc}=Zm_p+Nm_n-\Delta m \ . }
According to the Einstein relationship between mass and energy, the mass defect Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta m} is equivalent to an energy of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta E=\Delta mc^2} . Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta E} is the binding energy defined as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(Z,N)=(Zm_p+Nm_n-m_{nuc})c^2 \ . }
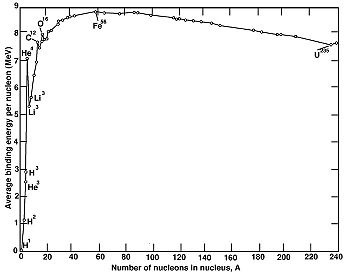
Figure 1 shows a plot of measured binding energies of the most stable isotopes for each mass number A. They usally have binding energies between 7 and 9 MeV per nucleon. Nuclides with mass numbers in the range of A=50-65 have the largest binding energies per nucleon.
Atomic mass and mass excess
Since the atomic mass can be measured with high precision, experimental mass evaluations tabulate atomic rather than nuclear masses. And they are related by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{atom}(A,Z)=m_{nuc}(A,Z)+Zm_e-B_e(Z) \ , }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_e} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_e} are the electron mass and the electron binding energy in the atom, respectively.
The so called atomic mass excess is defined by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M.E=(m_{atom}-Am_u)c^2 \ , }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is the mass number and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_u} denotes the atomic mass unit, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} , which is defined as one-twelfth of the mass of the neutral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{12}C} atom.
Nuclear models
In this chapter we discuss three models of nucleus.
Fermi gas model
Neutron and protons are viewed as distinguishable fermions, and the nucleus is assumed to be a cold Fermi gas in equilibrium, i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_F >> kT} . So if we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} fermions in a fixed nuclear volume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} , then the number of nucleons that can be contained in this certain volume of phase space is given by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dn(p)=\frac{4\pi p^2\Omega}{(2\pi\hbar)^3}dp} , where the nuclear volume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega =\frac{4\pi}{3}r_o^3A}
By integrating the above equation up to the Fermi level, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p = p_f} and equating it to the total number of nucleons Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} yields:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_f^3 = \frac{9\hbar^3\pi}{8r_o^3}}
If the potential is assumed to be a box-like, then the Fermi energy is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_F = \frac{\hbar^2k_F^2}{2m} = \frac{\hbar^2}{m}\left(\frac{3}{8\pi}\frac{N}{V}\right)^{2/3} \ .}
The mean energy per nucleon can be calculated using the Fermi-Dirac distribution formula for cold Fermi gas
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{E} = \frac{3}{5} E_F \ ,}
that is in the range of 8-12 MeV. note: the average number of nucleons in a nucleus is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{avg} = \frac{3}{4} p_f}
Liquid drop model
This model treats the nucleus as a drop of incompressible nuclear fluid, first proposed by G. Gamow and developed by N. Bohr and J. A. Wheeler. The first semi-empirical formula was obtained by Carl von Weizsäcker. According to this model the binding energy is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(Z, N) = a_V A - a_S A^{2/3} - a_C Z^2A^{-1/3} - a_{sym} \frac{(N-Z)^2}{A} +B_{pair}(Z, N) \ , }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_V = 16 \ MeV} and accounts for volume effect, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_S = 18.5 \ MeV} and is due to the surface effect, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_C = 0.72 \ MeV} and the term associated with it is due to the Coulomb repulsion of protons, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{sym} = 23.4 \ MeV} and the associated term is due to Pauli exclusion principle and is known as asymmetry effect and the last term is due to Cooper pairs.
Shell model
This model uses the Pauli principle to describe the structure of nucleus in terms of energy levels.The shell model not only predicts the properties of closed shell nuclei, but also the properties of nuclei with partly filled shells. When adding nucleons (protons or neutrons) to a nucleus, there are certain points where the binding energy of the next nucleon is significantly less than the last one.
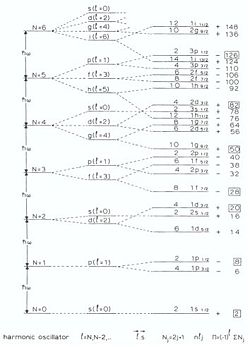
There are certain magic numbers of nucleons: 2, 8, 20, 28, 50, 82, 126 which are more tightly bound than the next higher number. In Figure 2 shown in the right we can see the Low energy levels in a single-particle shell model with an oscillator potential, where the number in the boxes are the magic numbers.
Two basic assumption of this model are that the interactions between one nucleon and the rest of the other nucleons can be understood by an average potential accompanied with a strong spin-orbit coupling term, and that a singe particle can move independently in the potential and is described by a single particle state of discrete energy and constant angular momentum.
Example: (ground state spin prediction) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Li^{11}:_{8n: \; all paired \to 0^+ }^{3p: \;(1s \frac{1}{2})^2 \;(1p \frac{3}{2})^1 \; \to -\frac{3}{2}} \! J^\pi (Li^{11}(g.s.))= -\frac{3}{2}}
Single Particle Potentials commonly used in the Nuclear shell model:
The Woods-Saxon Potential,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r) = -\frac{V_o}{1+exp(\frac{r-R}{a})}}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_o} represented the potential well depth, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is a surface thickness, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R=r_oA^\frac{1}{3}}
The well known Simple Harmonic Oscillator,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r) = \frac{1}{2}m\omega ^2x^2}
Along with these single-particle potentials a strong spin-orbit coupling term is included.