3rd Week: Equation of State & Basic Properties of Nuclei
Equation of State
With the relations shown in the 2nd week summary for the pressure P, the number of particles density n and the energy density u, equations of state for gases with different physical properties can be obtained. Several cases were analyzed in class: Photon gas, Boltzmann gas and three cases of non degenerate Fermi gas. Repeating all the mathematical steps that we have in the notes is a tedious work , however some important remarks can be made about the studied cases:
Photon Gas
Photons are bosons which will follow Bose-Einstein statistics (we found this in the first homework assignment), but have a very special feature. Unlike other bosons, photons do not have a chemical potential. The major properties of a photon gas then can be summarized as follows:
Number Density: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \int_0^\infty{8\pi\nu^2 \over c^3} {1 \over e^{h\nu \over kT}-1} d\nu = {(2.404) 8\pi k^3 \over 15h^3c^3}T^3}
Energy Density: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = \int_0^\infty{8\pi\nu^3 \over c^3} {1 \over e^{h\nu \over kT}-1} d\nu = {8\pi^5k^4 \over 15h^3c^3}T^4 = aT^4}
Pressure: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = {1 \over 3} \int_0^\infty 4\pi {2 \over h^3} {h\nu \over c}^2 {1 \over e^{h\nu \over kT}-1} c {h\nu \over c} {h \over c} d\nu }
Boltzmann Gas
The Boltzmann gas represents the ideal situation where the particles do not interact at all. This is the gas more commonly known as the "ideal gas".
Number Density: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \int_0^\infty 4 \pi {g \over h^3} p^2 e^{-E-\mu \over kT} dp =e^{\mu \over kT} {g \over h^3} \left(2\pi mkT\right)^{3/2} }
Energy Density: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = \int_0^\infty E {n 4 \pi p^2 \over \left( 2 \pi mkT \right)^{3/2} } e^{-p^2 \over 2mkT} dp = {3 \over 2} kT}
Pressure: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = {1 \over 3} \int_0^\infty pv {n 4 \pi p^2 \over \left( 2 \pi mkT \right)^{3/2}} e^{-p^2 \over 2mkT} dp = nkT }
Non-Relativistic Degenerate Fermi Gas
This case involves the particles of the gas to be so tightly packed that the electron clouds are touching and keeping the atoms apart. These kinds of gases are easily found in astrophysical situations such as white dwarf stars, which are electron degenerate, and in neutron stars. The equation of state for this kind of gas can be summarized by (full derivation was done as a part of the first homework):
Number Density: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = 4\pi { \left(2\pi mkT\right)^{3/2} \over h^3} F_{1/2}\left(- {\mu \over KT}\right)}
Pressure: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = {2 \over 3} nkT {F_{3/2}\left(- {\mu \over KT}\right) \over F_{1/2}\left(- {\mu \over KT}\right)} }
Basic Properties of Nuclei
The fundamental constituents of nuclei are protons and neutrons, also called nucleons. Is common to express the mass of these particles in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{MeV}/c^2} . The current accepted values are:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_p=938.272 \mathrm{MeV}/c^2 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_n=939.565 \mathrm{MeV}/c^2 } .
Today we know that protons and neutrons are not fundamental particles, they are formed by quarks, but for this introduction the internal structure of nucleons is not important. Nuclei can be characterized by several quantities like its mass number A, the number of protons Z, the number of neutrons N (clearly A=Z+N) and its charge eZ (being e the fundamental charge), although some of these are related. An important fact is that for stable nuclei the total mass is less than the mass of its protons plus the mass of its neutrons. This is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\left(Z,N\right)<Zm_p+Nm_n }
This is because there is a binding energy that keeps nucleons together preventing them from being repulsed by Coulomb interaction. The binding energy is simply given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B\left(Z,N\right)=Zm_p+Nm_n-m\left(Z,N\right)}
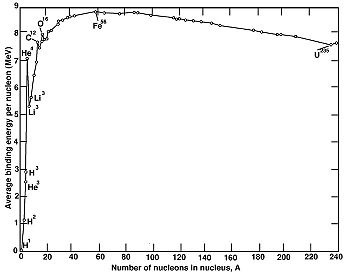
A plot of the experimental values of the binding energy as a function of the mass number is shown in Figure 1 (Originally uploaded by M. Avila).
Nuclear Models
There are several models that have been developed for understanding the structure of nuclei. Among the most important we can find the droplet, Fermi gas and shell model.
Fermi Gas Model
This model focuses on single particle properties. It considers the nucleus as a gas of non-interacting fermions where protons and neutrons have different densities, namely Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_p} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_n} respectively. The fermi gas model was among the first to incorporate quantum mechanics into nuclear structure. Protons differ from neutrons in that they carry an electric charge therefore there potential is different than neutrons. As in other Fermi gases the Fermi energy plays a major roll and is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{Fx}=\frac{\hbar^2}{2m}(\frac{3}{g}\pi^2\rho_x)^{2/3}}
where g is the degeneracy factor and the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} denotes that this quantity can be calculated for protons and for neutrons. From this formula and the relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{Fx}=\hbar^2 k_{Fx}^2/2m} we can get the magnitude of Fermi wave-vector
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{Fm}=(\frac{3}{g}\pi^2\rho_x)^{1/3}}
The average kinetic energy per particle is the sum (integral) of all the occupied single particle states over the density of particles
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{E}= \frac{1}{\rho_x}\frac{g m^{3/2}}{\pi^2\sqrt{2}\hbar^3} \int_0^{\epsilon_{Fx}}\epsilon^{3/2}d\epsilon = \frac{3}{5}\epsilon_{Fx}}
For a mixture of protons and neutrons we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{E}= \frac{3}{5}\frac{N \epsilon_{Fn}+Z \epsilon_{Fp}}{A}}
If the density of particles in the nucleus is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_0}
it should satisfy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_0=\rho_p+\rho_n}
, then the densities of the protons and neutrons can be written in a symmetric form
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_p=\frac{Z}{A}\rho_0=\frac{\rho_0}{2}(1+\frac{Z-N}{A})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_n=\frac{N}{A}\rho_0=\frac{\rho_0}{2}(1-\frac{Z-N}{A})}
It should be noted that this model only works if the nucleus is in its ground state or at absolute zero.
Droplet Model
Unlike the fermi gas model the liquid drop model allowed to treat all nucleons as a "simple drop" as the name implies. This phenomenological model was accountable for the binding energy. The liquid drop models does not take into consideration the individual quantum properties of nucleons. The liquid drop allows the strong force to be saturated among the core and a weaker binding on the surface. The liquid drop model can calculate the binding energy by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B.E.= a_V A- a_s A^{2/3} -a_C\frac{Z^2}{A^{1/3}}-a_{sym}\frac{(N-Z)^{2}}{A} +B_{pair}(Z,N)} ,
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_V} is equal to the volume energy for uniform binding, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_s} compensates for inaccurate estimations for surface tension, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_C} takes into consideration the coulomb repulsion, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{sym}} allows for the stability of when the number of neutrons equals the number of protons, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_{pair}(Z,N)} is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 12/\sqrt{A}} for even-even nuclei, zero for odd A and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -12/\sqrt{A}} for odd-odd nuclei. The coefficients Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{V}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{s}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{C}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{sym}} fit experimentally measured values of 15.6 MeV, 16.8 MeV, 0.72MeV, 23.3 MeV, respectively.
Shell Model
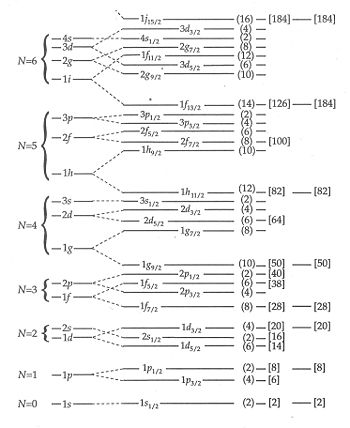
This is considered as a phenomenological single particle model because much of its parameters are fitted to experimental results. According to Greiner and Maruhn (Nuclear Models, Springer 1995) the most important experimental result from this model is the prediction of the first couple of magic numbers:2, 8, 20, 28, 50, 82. The magic number 126 is established only experimentally for neutrons. The prediction for other magic numbers >100 depends on the theory chosen for superheavy nuclei. The shell model is based on the solution of Schrödinger's equation for single particle levels. Is common to use the potential for harmonic oscillator with spin coupling to orbital angular momentum. The energy states obtained with this potential are shown in Figure 2.
We present a list of the potentials that can be used in this model:
Woods-Saxon
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)=-\frac{V_0}{1+\exp[(r-R)/a]}}
with typical values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0=50} MeV, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R=1.1 \mathrm{fm}A^{1/3}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=0.5} fm.
Harmonic Oscillator
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)=\frac{1}{2}m\omega^2 r^2}
Spin-Orbit coupling (operator representation)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{V}=C \hat{\mathbf{l}}\cdot \hat{\mathbf{s}}}
Where:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C\hat{l}\hat{s}=C[J^{2}-L^{2}-S^{2}]=C[j(j+1)-l(l+1)-s(s+1)]}
With C being a constant, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\mathbf{l}}} the orbital angular momentum operator and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\mathbf{s}}} the spin operator.