5th Week: Reaction Rates, Nuclear Networks & NSE B
Reaction rate
The goal is to determine the change of abundances and energy and we define the reaction rate r as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma(v)=\frac{\mbox{number of reactions per second per targets}}{\mbox{flux of incoming particles}}=\frac{r_{ij}/n_i}{n_jv}}
So therefore what is needed is cross sections and velocity distribution of beam and target.
Non-degenerate Boltzmann Gas
The rates are written as
with
Particle-induced reactions
For a particular value of the relative velocity of the projectile particles (i) respect to the target particles (j) the relation of reaction rate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{ij}} and total cross section is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma(v)=\frac{\mbox{number of reactions per second per targets}}{\mbox{flux of incoming particles}}=\frac{r_{ij}/n_i}{n_jv}}
Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{ij} = n_i n_j v \sigma (v) \ , }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_j} are the number densities of interacting particles (in units of particles per volume) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} is the relative velocity of the projectile to the target. In a more realistic case we would have a velocity distribution. This is described by a probability distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(v)} . Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(v)dv} is the probability of the projectile to have a velocity between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v+dv} . The reaction rate can be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{ij}=\frac{n_in_j}{1+\delta_{ij}}\int_{0}^{\infty}v\sigma(v)P(v)dv}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{ij}=\frac{n_in_j}{1+\delta_{ij}}\langle\sigma v\rangle}
Here the factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1+\delta_{ij}} is to avoid double counting when the particles i and j are the same.
In most situations stellar plasma is non-degenerate and moves in a non-relativistic way, Thus the Maxwell-Boltzmann distribution can be used
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(v)dv=\left( \frac{m_{ij}}{2\pi kT} \right) ^{3/2} e^{-m_{ij}v^2/2kT}4\pi v^2 dv}
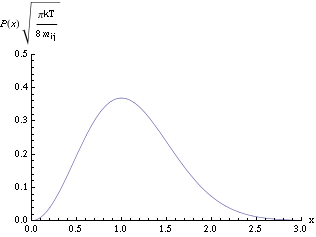
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{ij}=m_i m_j/(m_i +m_j)} is the reduced mass. A graph of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)(\pi kT/8m_{ij})^{1/2}} versus x is shown in Figure 1 where we have defined Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = v (m_{ij}/2kT)^{1/2}} . It can be found that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(v)} has a maximum at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{T}=(2kT/m_{ij})^{1/2}} . This is called the thermal velocity.
Photon-induced reactions
These reactions have the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i(\gamma,m)o} and are also called photodisintegration reactions. The reaction rate can be obtained using the energy of the photon Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\gamma}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{i\gamma}=n_i \int_{E_t}^{\infty} cn_{\gamma}(E_{\gamma})\sigma(E_{\gamma})dE_{\gamma} }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_t\geq 0} is the threshold energy of the reaction. The decay probability is just the ratio of the reaction rate upon the number of particles i
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{i\gamma}=\frac{r_{i\gamma}}{n_i} }
The number of photons with energy between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\gamma}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\gamma}+dE_{\gamma}} can be found using Planck's distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{\mbox{P}}(E_{\gamma})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{\gamma}(E_{\gamma})dE_{\gamma}=\frac{f_{\mbox{P}}(E_{\gamma})}{E_{\gamma}}dE_{\gamma}}
.
with
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{\mbox{P}}(E)=\frac{8\pi}{(hc)^3}\frac{E^3}{e^{E/kT}-1}}
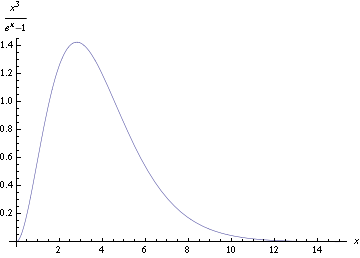
A plot of the unitless function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (hc)^3f_P/8\pi (kT)^3} versus Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=E/kT} is shown in Figure 2.
Finally we can write the decay probability as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{i\gamma}= \frac{8\pi}{h^3 c^2} \int_{E_t}^{\infty} \frac{E_{\gamma}^2}{e^{E_{\gamma}/KT}-1}\sigma(E_{\gamma})dE_{\gamma}}
Reciprocity theorem
This is a very useful theorem that relates the cross sections of reversed reactions like Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i(j,o)m} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m(o,j)i} . This theorem states that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\sigma_{om\rightarrow ij}}{\sigma_{ij\rightarrow om}}=\frac{g_i g_j}{g_o g_m} \frac{p_{ij}^2}{p_{om}^2}\frac{(1+\delta_{om})}{(1+\delta_{ij})}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_x=2s_x+1} is the spin degeneracy factor of particle x and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{om}} (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{ij}} ) is the magnitude of the relative momentum of particle o (i) respect to m (j). For non-relativistic spin 1/2 particles and with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{ab}^2=2m_{ab}E_{ab}} we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\sigma_{om\rightarrow ij}}{\sigma_{ij\rightarrow om}}=\frac{m_{ij}E_{ij}}{m_{om}E_{om}}\frac{(1+\delta_{om})}{(1+\delta_{ij})}}
For the case of photodesintegration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{i\gamma}^2=E_{\gamma}^2/c^2} , then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\sigma_{om\rightarrow i\gamma}}{\sigma_{i\gamma\rightarrow om}}=\frac{2g_i}{g_og_m}\frac{E_{\gamma}^2}{2c^2m_{om}E_{om}}\frac{(1+\delta_{om})}{1}}
Nuclear Networks
A nuclear reaction network for the reaction of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i(j,o)m} would be as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{Y}_{i}=-\frac{1}{1+\delta_{ij}}\rho N_{A}\langle\sigma v\rangle_{ij}Y_{i}Y_{j} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{Y}_{j}=-\frac{1}{1+\delta_{ij}}\rho N_{A}\langle\sigma v\rangle_{ij}Y_{i}Y_{j} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{Y}_{o}= \frac{1}{1+\delta_{ij}}\rho N_{A}\langle\sigma v\rangle_{ij}Y_{i}Y_{j} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{Y}_{m}= \frac{1}{1+\delta_{ij}}\rho N_{A}\langle\sigma v\rangle_{ij}Y_{i}Y_{j} }
The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1+\delta_{ij}} term is used to prevent double counting in reactions where the same particles interact.
For decays and captures the network looks as follows:
Nuclear Statistical Equilibrium
Under certain conditions, the isotope formation is no longer dependent on reaction rates. One first needs to make three assumptions. First the nuclear time scale needs to be much less than the hydrodynamical time scale. Second one is dealing with a boltzmann gas. And finally the gas must be in chemical equilibrium. In this regime the reactions are solely dependent on electron capture. The elements formed this way follow the following rules.