6th Week: The Early Universe and Big Bang Nucleosynthesis

The Big Bang Cosmology

Cosmological principle

The cosmological principle, which is the more general version of the Copernican principle, states that on large spatial scales, the Universe is homogeneous and isotropic. This means that there is no special point in the Universe. Homogeneity of the universe means that the universe has the same property at any regions from point to point. Isotropy of the universe means that the universe looks the same from all directions. We know that at small scales the universe is not homogenous and not isotropic otherwise any structures e.g. galaxies, stars, planets and humans would not even exist. However provided that we consider the universe on average on large scales, it looks approximately homogenous and isotropic. The observed cosmological scales are therefore approximately Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 300} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 500} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Mpc} in which the cosmological principle works.

The expanding Universe

Before 1915, it was believed that the cosmos was static and infinite. But the infinite Universe (Newtonian Universe) was ruled out soon due to the Olbers paradox, that states for such a Universe the dark night should not exist. The Einsteins theory of gravitation suggested that the Universe is no more static. But however in order to get a static Universe solution Einstein added a so called cosmological constant, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} which later he called it his greatest blunder. In 1922 Friedmann solved the Einsteins equations for isotropic and homogeneous universe and found that the Universe is either expanding or collapsing. This was experimentally discovered (the galaxies of the universe all receed from each other) by Hubble in 1928, that the Universe is expanding and the expansion law is the following

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v} = H_0 \vec{R} \ , }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0} is the so called Hubble constant, which at present believed to be

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0 = 70.1 \pm 1.3 \quad (km/s)/Mpc \ . }

The Hubble "constant" is not a constant, but is actually a time varying quantity. Defining a scale factor, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{R} = a \vec{x} \ , }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{x}} is the comoving coordinate, one can find the folowing relation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{o} = \frac{\dot{a}(t_{o})}{a(t_{o})} \ . }

Friedmann equations

From the large-scale distribution of galaxies and the near-uniformity of the CMB temperature, we have good evidence that the universe is nearly homogeneous and isotropic.

Under this assumption, the space-time metric can be written in the form

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ds^2 = -c^2dt^2 + a^2(t)\left[\frac{\mathrm{d}r^2}{1-k r^2} + r^2 \mathrm{d}\mathbf{\Omega}^2\right] \ , }

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{d}\mathbf{\Omega}^2 = \mathrm{d}\theta^2 + \sin^2 \theta \, \mathrm{d}\phi^2 \ . }

There are two independent Friedmann equations for modeling a homogeneous, isotropic universe. They are:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^2 = \left(\frac{\dot{a}}{a}\right)^2 = \frac{8 \pi G}{3} \rho - \frac{kc^2}{a^2} + \frac{\Lambda c^2}{3}}

which is derived from the 00 component of Einstein's field equations, and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{H} + H^2 = \frac{\ddot{a}}{a} = -\frac{4 \pi G}{3}\left(\rho+\frac{3p}{c^2}\right) + \frac{\Lambda c^2}{3}}

which is derived from the trace of Einstein's field equations.

Figure 1. Three Dimensional Euclidean Space curvature

Using the first equation, the second equation can be re-expressed as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{\rho} = -3 H \left(\rho + \frac{p}{c^2}\right) \ , }

which eliminates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda \!} and expresses the conservation of mass-energy.

Now remembering to consider that our geometry is in Euclidean space with time as dimension also.

If the scale factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is taken to be 1 at the present time, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} describes the spatial curvature when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = 1} (i.e. today).

Figure 2. The fate of the Universe based on space curvature

We arise with three possible scenarios.

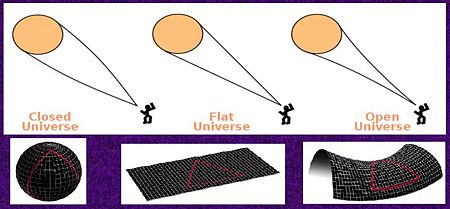
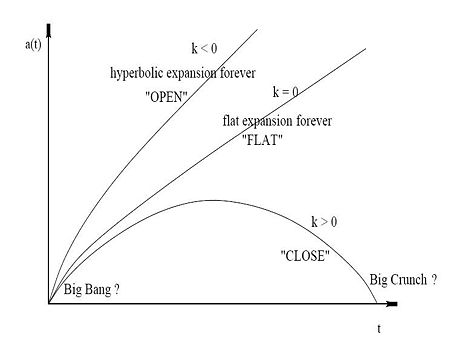
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is positive, then the Universe is geometrically viewed as a hyperspherical, or also called as a closed Universe.

In the closed Universe the expansion stops at some point and then recollapses to a Big Crunch.

If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is zero, then the universe is flat.

The flat Universe expands forever.

If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is negative, then the universe is hyperbolic in geometry and also called an open Universe.

The open Universe expands with acceleration and the end result is known as the Big Chill.

for arbitrary k and a mixture of vacuum energy and relativistic and non-relativistic matter, we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \;\; \rho = \frac{3H_{o}^{2}}{8\pi G}\left [\Omega _{\Lambda } +\Omega _{M }(\frac{a_{o}}{a})^{3}+\Omega _{R }(\frac{a_{o}}{a})^{4}\right ]}

where the sum of the fractions of the critical energy density

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega _{\Lambda } +\Omega _{M }+\Omega _{R}+ \Omega _{k}= 1, \Omega _{k}\equiv -\frac{k}{a_{o}^{2}H_{o}^{2}}}

Solution of the Friedmann equations

For simplicity, from now on we work in the units of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c=1} . Then the fluid equation is just

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dot{\rho} = -3 H \left(\rho + p\right) \ . }

The equation of state generally can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p = w \rho \ , }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w=0} for cosmological dust, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w=1/3} for radiation, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w=-1} for cosmological constant or vacuum energy. The general solution is then

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho =\rho_0 \left(\frac{a}{a_0}\right)^{-3(1+w)} \ . }

And the solution to the Friedmann equation gives

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a =a_0 \left(\frac{t}{t_0}\right)^{2/[3(1+w)]} \ . }

Evolution of density with time

Putting the las two equations together we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(t) = \rho_0 \left(\frac{t}{t_0}\right)^{-2} \ , }

where the subscript Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} denotes as the quantity for today. Thus, the density evolves the same regardless of the type of the fluid. Further substitution defines the Hubble constant in terms of time

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(t) = \left(\frac{2}{3(1+w)}\right)\frac{1}{t} \ . }

Relying on the observation of Hubble constant and using the equation of state parameter one can find the approximate age of the Universe. For a dust-filled Universe this time is equal to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0 = \frac{2}{3H_0} \approx 9.2 \times 10^9 \quad years \ . }

Primordial Nucleosynthesis

We now look back at a time when the temperature of the universe was between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{4}K } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{11}K}

Big bang nucleosynthesis begins with the individual baryons: protons and neutrons. The neutrons are unstable as free particles but due to the shortness of time during the nucleosynthesis era of the big bang, their abundance is only slightly reduced by this decay. Primordial nucleosynthesis took place just a few minutes after the Big Bang and is believed to be responsible for the formation of a heavier isotope of hydrogen known as deuterium (H-2 or D), the helium isotopes He-3 and He-4, and the lithium isotopes Li-6 and Li-7. In addition to these stable nuclei some unstable, or radioactive, isotopes were also produced during primordial nucleosynthesis: tritium or H-3; beryllium-7 (Be-7), and beryllium-8 (Be-8). These unstable isotopes either decayed or fused with other nuclei to make one of the stable isotopes.

The reactions on the free nucleons, the proton and the neutron, are most important in the time of beta equilibrium and, after freeze out, when the weak reactions eventually end reacting slower than the cooling time and the free neutrons decay.

Less than 1 second after the Big Bang, the reactions shown at right maintain the neutron:proton ratio in thermal equilibrium. About 1 second after the Big Bang, the temperature is slightly less than the neutron-proton mass difference, these weak reactions become slower than the expansion rate of the Universe, and the neutron: proton ratio freezes out at about 1:6.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p + e^- \rightleftharpoons n + \nu \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n + e^+ \rightleftharpoons p + \bar{\nu} \ . }

After 1 second, the only reaction that appreciably changes the number of neutrons is neutron decay, shown at right. The half-life of the neutron is 615 seconds. Without further reactions to preserve neutrons within stable nuclei, the Universe would be pure hydrogen.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \rightarrow p + e^- + \bar{\nu} \ . }

At Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.3} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MeV} , nuclei become favoured over free nucleons. Apparently here, the production rate is larger than the photon destruction rate. All free neutrons left (number of neutrons after freeze out minus number of neutrons destroyed due to free neutron decay) get bound up to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle He^{-4}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{freeze}= 1.5 \times 10^{4}K (\Omega _{B}h^{2}) \ .}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega _{B}h^{2}=0.0214\pm 0.0020}

Most of the mass in the universe is not in the form of ordinary baryonic matter (electrons & atomic nuclei).

The reaction that preserves the neutrons is deuteron formation. The deuteron is the nucleus of deuterium, which is the heavy form of hydrogen (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^2} ). This reaction is exothermic with an energy difference of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2.2} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MeV} , but since photons are a billion times more numerous than protons, the reaction does not proceed until the temperature of the Universe falls to 1 billion K or $kT=0.1MeV$, about 100 seconds after the Big Bang. At this time, the neutron:proton ratio is about 1:7.

$p+n\rightleftharpoons d+\gamma \ .$

Once deuteron formation has occurred, further reactions proceed to make helium nuclei. Both light helium ($He^{3}$) and normal helium ($He^{4}$) are made, along with the radioactive form of hydrogen ($H^{3}$). These reactions can be photoreactions as shown here. Because the helium nucleus is $28$ $MeV$ more bound than the deuterons, and the temperature has already fallen so far that kT = 0.1 MeV, these reactions only go one way.

$d+n\rightarrow H^{3}+\gamma \ ,$

$H^{3}+p\rightarrow He^{4}+\gamma \ ,$

$d+p\rightarrow He^{3}+\gamma \ ,$

$He^{3}+n\rightarrow He^{4}+\gamma \ .$

Puzzlement of the Big Bang Theory

Despite the self-consistency and remarkable success of the standard Hot Big Bang model in describing the evolution of the universe back to only one hundreth of a second, a number of unanswered questions remain regarding the initial state of the universe. These difficulties are not so much errors as they are assumptions that are necessary but that do not have a fundamental justification. The required discussion is technical, so we will be content with a rather superficial statement of the three basic problems that are associated with the big bang and how they might be cured by a new idea that arises from considering the implications of elementary particle physics for cosmology.

Flatness

Figure 3.

The flatness problem was first mentioned by Robert Dicke in 1969. It is a cosmological fine-turning problem, and the most accepted solution is cosmic inflation, along with the monopole problem and the horizon problem.

The problem is that that the density of the universe is close to its critical value at which space is flat.Since the total energy density of the universe departs rapidly from the critical value over cosmic time, this implies that the early universe must have had a density even closer to the critical density. This problem leads to the cosmologists to the question how the density of the early universe came to be fine-tuned to this special value.

As we mentioned the most accepted explanation is that the cosmic inflation's rapid expansion caused a flat universe. So independently of the initial value of omega after the tremendous burst of expansion omega becomes one.

Imagine living on the surface of a soccer ball (a 2-dimensional world). It might be obvious to you that this surface was curved and that you were living in a closed universe. However, if that ball expanded to the size of the Earth, it would appear flat to you, even though it is still a sphere on larger scales. Now imagine increasing the size of that ball to astronomical scales. To you, it would appear to be flat as far as you could see, even though it might have been very curved to start with. Inflation stretches any initial curvature of the 3-dimensional universe to near flatness.

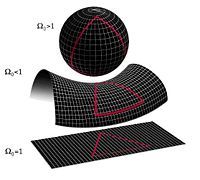
In the Figure 3. as mentioned before in Friedmann equations section, we can see that for $\Omega >1$ the universe is curved like a sphere, for $\Omega >1$ is hyperbolic and for $\Omega =1$ the universe is flat.

Horizons

So in assuming standard Big Bang expansion, we come to realize that distant regions of space in opposite directions of the sky are so far apart, that they in turn could never have been in causal contact with each other. This is due in part to that the light travel time between them exceeds the age of the universe. Yet the uniformity of the cosmic microwave background temperature tells us that these regions must have been in contact with each other in the past. A conundrum we have indeed.

The puzzlement we come across here arises from the much high degree of isotropy of the Cosmic Microwave Background.

the proper horizon size at the time of last scattering $t_{L}$

$d_{H}(t_{L})\equiv a(t_{L})\int _{t_{\ast }}^{t_{L}}{\frac {dt}{a(t)}}$

we set the beginning of the era of inflation at $t_{\ast }$

here contributions from the matter and radiation dominated eras is apparently way too small to account for the isotropy of the microwave radiation background that we see today. As a result we must assume that the integral is dominated by an era of inflation.

and we make the assumption that a(t) increased so at a rate of $H_{I}$ in an exponential way during this inflation period.

$a(t)=a(t_{\ast })exp(H_{I}(t-t_{\ast }))=a_{I}exp(-H_{I}(t_{I}-t))$

$d_{H}(t_{L})={\frac {a(t_{L})}{a_{I}H_{I}}}\left[e^{N}-1\right]$

at large angular scales we have to account for the cosmic microwave background high degree of isotropy

$d_{H}(t_{L})>d_{A}(t_{L})$

where the angular diameter distance of the surface of last scattering is found here to be

$d_{A}(t_{L})={\frac {a(t_{L})}{a_{o}H_{o}}}$

we now have the condition for the isotropy of the cosmic microwave background, which comes to be

$e^{N}>{\frac {a_{I}H_{I}}{a_{o}H_{o}}}$

we make the assumption here that really not much happens between the end of inflation and the radiation-dominated era.

Monopoles

Inflation allows for magnetic monopoles to exist as long as they were produced prior to the period of inflation. As previously mentioned, during inflation, the universe expands exponentially at least to 64 $e$-folds. As the actual number of monopoles is not increasing during this time, the monopole density dramatically increases, so dramatically in fact that in todays universe they are virtually undetectable.

As a bonus, inflation also explains the origin of structure in the universe. Prior to inflation, the portion of the universe we can observe today was microscopic, and quantum fluctuation in the density of matter on these microscopic scales expanded to astronomical scales during inflation. Over the next several hundred million years, the higher density regions condensed into stars, galaxies, and clusters of galaxies.

Big Bang cosmology predicts that a very large number of heavy, stable "magnetic monopoles" should have been produced in the early universe, which should be abundant enough for us to easily detect. However, magnetic monopoles have never been observed in the laboratory (or anywhere else for that matter). This contradiction presents a problem in our cosmological assumptions. One theory which is becoming widely accepted, and seeks to deal with the cosmological problems of monopole, horizons, and flatness, is known as Inflation.

Inflation

A sort of solution to the cosmological problem is the cosmic inflation, a process where the universe expands very quickly in a short period of time. The theory of inflation developed by Alan Guth, Andrei Linde, Paul Steinhardt, and Andy Albrecht, offers solutions to the the cosmological problems of the flatness universe, the horizon and several other open questions in cosmology. It proposes a period of extremely rapid (exponential) expansion of the universe prior to the more gradual Big Bang expansion, during which time the energy density of the universe was dominated by a cosmological constant-type of vacuum energy that later decayed to produce the matter and radiation that fill the universe today.

Inflation was both rapid, and strong. It increased the linear size of the universe by more than 60 "e-folds", or a factor of ~10^26 in only a small fraction of a second! Inflation is now considered an extension of the Big Bang theory since it explains the above puzzles so well, while retaining the basic paradigm of a homogeneous expanding universe. Moreover, Inflation Theory links important ideas in modern physics, such as symmetry breaking and phase transitions, to cosmology. The theory of inflation addresses the aforementioned problems.

The idea is that the cause of inflation is a field which permeates space and drives the expansion. This field contains a certain energy density, which roughly constant as space expands. So from Friedman Equation we have

$(\Omega ^{-1}-1)\rho a^{2}={\frac {-3kc^{2}}{8\pi G}}\ .$

Looking at this expression we can see that since the density is constant the term $\rho a^{2}$ increases extremely rapidly as the scale factor a grows exponentially. Thus the sensitive dependence on the initial value of $\Omega$ has been removed. Therefore no matter what the initial value of $\Omega$ is, Inflation's rapid expansion caused space to become flatter, forcing omega to be one.

Inflation Relating to:

The Flatness Problem

Imagine living on the surface of a soccer ball (a 2-dimensional world). It might be obvious to you that this surface was curved and that you were living in a closed universe. However, if that ball expanded to the size of the Earth, it would appear flat to you, even though it is still a sphere on larger scales. Now imagine increasing the size of that ball to astronomical scales. To you, it would appear to be flat as far as you could see, even though it might have been very curved to start with. Inflation stretches any initial curvature of the 3-dimensional universe to near flatness.

The Horizon Problem

Distant regions of space in opposite directions of the sky are so far apart that, assuming standard Big Bang expansion, they could never have been in causal contact with each other. This is because the light travel time between them exceeds the age of the universe. Yet the uniformity of the cosmic microwave background temperature tells us that these regions must have been in contact with each other in the past.

The Monopole Problem

Inflation allows for magnetic monopoles to exist as long as they were produced prior to the period of inflation. As previously mentioned, during inflation, the universe expands exponentially. As the actual number of monopoles is not increasing during this time, the monopole density dramatically, so dramatically in fact that in todays universe they are virtually undetectable.

As a bonus, Inflation also explains the origin of structure in the universe. Prior to inflation, the portion of the universe we can observe today was microscopic, and quantum fluctuation in the density of matter on these microscopic scales expanded to astronomical scales during Inflation. Over the next several hundred million years, the higher density regions condensed into stars, galaxies, and clusters of galaxies.