8th Week: Reaction flows, pp- and CNO-cycle & Solar Neutrinos
Steady flow in nuclear reactions
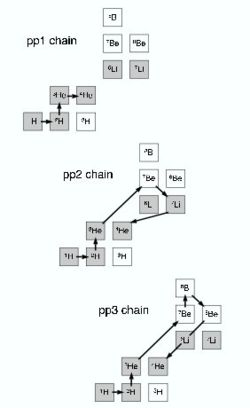
The pp-chain(s)
As we have seen before in the previous wiki page, the pp chains statrts from hydrogen and converts four protons to one Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^4He } nucleus,with two Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta } decays or electron captures among the intermediate reactions.
The following three sequences of nuclear processes are referred to as proton–proton, or pp chains:
| pp1 chain | pp2 chain | pp3 chain |
|---|---|---|
| Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(p,e^+ \nu)d } | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(p,e^+ \nu)d } | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p(p,e^+ \nu)d } |
| Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d(p,\gamma)^3 He } | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d(p,\gamma)^3 He } | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d(p,\gamma)^3 He } |
| Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^3He(^3He,2p)\alpha} | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^3He(^3He,2p)\alpha } | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^3He(^3He,2p)\alpha } |
| Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^7Be(e^−,\nu)^7Li } | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^7Be(p,\gamma)^8B } | |
| Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^7Li(p,\alpha)\alpha } | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^8B(\beta ^+,\nu)^8Be } | |
| Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^8Be(\alpha)\alpha } | ||
The chains are also displayed in Figure 1. The first two reactions are the same for each chain. Other nuclear reactions involving the light nuclei Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^1H }
, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^2H}
, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^3He}
, and so on, are less likely to occur in stars
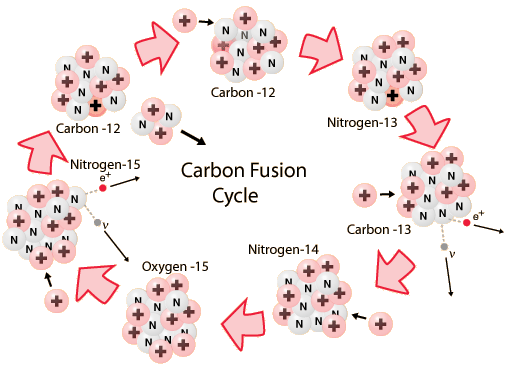
CNO-cycle(s)
In stars with central temperatures greater than 15 million Kelvin, carbon fusion is thought to take over the dominant role rather than hydrogen fusion. The main theme of the CNO cycle is the adding of protons, but after a carbon-12 nucleus fuses with a proton to form nitrogen-13, one of the protons decays with the emission of a positron and a neutrino to form carbon -13. Two more proton captures produce nitrogen-14 and then oxygen-15. Another neutron decay leaves nitrogen-15. Another proton capture produces oxygen-16 which emits an energetic alpha particle to return to carbon-12 to repeat the cycle. This last reaction is the main source of energy in the cycle for the fueling of the star.
While this process is not a significant part of the sun's fuel cycle, a star like Sirius with somewhat more than twice the mass of the sun derives almost all of its power from the carbon cycle. The carbon cycle yields 26.72 MeV per helium nucleus.A Diagram on the CNO Cycle is given here:
Solar neutrinos
Solar neutrinos are produced by the weak nuclear reactions that power the Sun. They are produced, in particular, during the pp-chain reactions written above and the CNO cycles. For example, they are produced mainly due to the following reaction,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p+p \rightarrow D + e^+ + \nu_e \ , }
where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_e} has the energy of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.27} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MeV} . The other possible reactions from the pp-chain are
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^7Be + e^- \rightarrow ^7Li + \nu_e \ , }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^8B \rightarrow ^8Be + e^+ +\nu_e \ , }
with less probabilities and the energies of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.86} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MeV} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6.84} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MeV} , respectively.
There are three neutrino's flavors: electron neutrino, muon neutrino, and tau neutrino, dubbed as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_{e}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_{\mu}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_{\tau}} , respectively. Correspondingly, there are three flavor eigenstates. If, neutrinos have mass, then there are also three mass eigenstates, that are mixed together
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_{f} = \sum_{m=1}^n U_{fm} \nu_{m} \ , }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} is the number of mass eigenstates and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} is an orthonormal mixing matrix.
Solar neutrino problem
For almost four decades there was a major disagreement in the measurements of the numbers of neutrinos flowing through the Earth and theoretical models of the solar interior. In particular, in the first neutrino experiment, the measured neutrino solar fluxes at the Earth have been smaller by a factor of about 3 compared to those expected from the luminosity of the Sun. Possible solutions have considered have been astrophysical, nuclear, and in the properties of neutrinos.
Early nuclear and astrophysical attempts to explain the disagreement proposed that the models of the sun were wrong, i.e. the temperature and pressure in the interior of the Sun were very different from what was believed. For example, since neutrinos measure the amount of current nuclear fusion, it was suggested that the nuclear processes in the core of the Sun might have temporarily shut down. Since it takes thousands of years for heat energy to move from the core to the surface of the Sun, this would not immediately be apparent. But the advances in helioseismology (the study of how waves propagate through the Sun) and better measurement of neutrinos showed that this solution is wrong, i.e. the interior temperature of the Sun agrees with the standard solar models.
However, the discrepancy has since been resolved by the latter, by new understanding of neutrino physics, requiring a modification of the Standard Model of particle physics. Essentially, as neutrinos have mass, they can change from one flavor that had been expected to be produced in the Sun's interior into two other flavors that would not be caught by the detectors in use at the time. This is known as neutrino oscillations.
It is easy to give a flavor of how these oscillations might be, assuming that only two eigenstates are mixed. The weak eigenstates that we normally observe (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_{e}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_{\mu}} ) can oscillate between each other if they are composed of an add-mixture of mass eigenstates (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_{1}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_{2}} ). If the weak eigenstates are rotated by an angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} with respect to the mass eigenstates, then a matrix equation can be written that relates the weak eigenstates to the mass eigenstates
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} |\nu_{e}\rangle \\ |\nu_{\mu}\rangle \end{pmatrix}= \begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} |\nu_{1}\rangle \\ |\nu_{2}\rangle \end{pmatrix} \ . }
Introducing the time evolution of the flavor eigenstates, we could solve the problem of how the neutrinos could propagate in time. We do not bring all the calculations here, but give several steps. For example, at time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=0}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\nu_{\mu}\rangle = - \sin\theta |\nu_1 \rangle + \cos\theta |\nu_2\rangle \ . }
In general, this can be written as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\nu_{\mu}(t)\rangle = - \sin\theta |\nu_1\rangle e^{-\frac{E_1}{\hbar}t}+ \cos\theta |\nu_2\rangle e^{-\frac{E_2}{\hbar}t} \ , }
where the neutrinos are considered to be relativistic. After some manipulations, we can calculate the probability for a muon neutrino state to oscillate into an electron neutrino state.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(\nu_{\mu} \rightarrow \nu_e) = \left|\langle \nu_{e}|\nu_{\mu}(t)\rangle\right|^2 = \sin^2 2\theta \sin^2 \left(\frac{\Delta m^2}{4} \frac{L}{E_{\nu}} \right)}
Experiments to detect the neutrinos
The first experiment to detect the neutrinos took place in the Homestake Gold Mine in Lead, South Dakota, and therefore known as Homestake experiment or sometimes as Davis experiment. They placed 4,800 feet underground a 100,000 gallon tank of dry-cleaning fluid. A big target deep underground was needed to account for the very small probability of a successful neutrino capture, and to prevent interference from other forms of solar radiation. Upon collision with a neutrino, a chlorine atom in the fluid transforms into a radioactive isotope of argon, which can then be extracted and counted. The experiment was measured every few weeks, to count how many argons had formed, and therefore to determine how many neutrinos had been captured.
Later there were a list of experiments known as KamiokaNDE experiment (Kamioka Nucleon Decay Experiment). In the first Kamiokande experiment they built a large water Cherenkov detector designed to search for proton decay. To observe the decay of a particle with a lifetime as long as a proton an experiment must run for a long time and observe an enormous number of protons. This can be done most cost effectively if the target and the detector itself are made of the same material. A proton decay detector must be buried deep underground or in a mountain because the background from cosmic ray muons in such a large detector located on the surface of the Earth would be far too large. The muon rate in the KamiokaNDE experiment was about 0.4 Hz, roughly five orders of magnitude smaller than what it would have been if the detector had been located at the surface. The first astrophysical neutrinos actually were detected in this experiment, that lead to a Nobel prize in 2002.
In order to find the solution to the solar neutrino problem through neutrino oscillations, the so called Super Kamiokande detector was designed in 1996. It consists of 50,000 tons of pure water surrounded by about 11,200 photomultiplier tubes.
There are other experiments known as BNO (Baksan Neutrino Observatory), KamLAND (Kamioka Liquid Scintillator Antineutrino Detector), MINOS (Main Injector Neutrino Oscillation Search), MiniBooNE (Mini Booster Neutrino Experiment), Super-Kamiokande, Sciboone (SciBar Booster Neutrino Experiment), Borexino (Boron Experiment) that aim to detect neutrinos.