Geometrically Frustrated Materials

The main focus of solid state physics is on macroscopic properties of solid materials that result from interactions between atoms. Solid state physics is extremely interested in how these interaction come to an equilibrium to order in a certain way such as antiferromagnetism. One emergent property is disorder that arises from geometric frustration and this is the subject of much perplexing research because there seems to be no equilibrium between interactions or no unique ordering state.

Figure 1. The frustration that we are all familiar with.

What is geometric frustration?

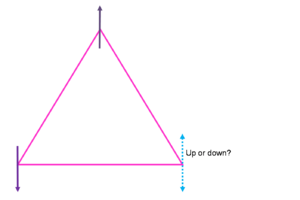
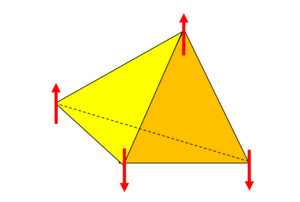
Frustration is the inability of a material to find a single ground state and instead has a highly degenerate ground state. The reason for this is because the geometry of the crystal is such that any arrangement of its constituent parts on the lattice cannot simultaneously satisfy all interactions. Most of the time this is referring to spins on a lattice in which the magnetic ordering is the subject of interest but this may also refer to the arrangement of oxygen and hydrogen atoms in water ice. In one dimension, consider a triangle with a spin on each vertex (see Fig.1). Two spins are satisfied and one spin is frustrated. That is, one spin can align up or down to satisfy a specific interaction but cannot satisfy all interactions. In three dimensions consider a tetrahedral where there is no possible configuration of four Ising spins on the vertices where they will all align antiferromagnetically (see Fig. 2). Both of these cases have competing interactions between the order of the lattice imposed on the local moments and the interactions between the moment themselves.

The size of the frustration parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} , defined by the ratio of the Curie-Weiss temperature and the expected mean field ordering temperature (Néel or Curie temperature) or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\theta_{CW}}{T_N}} , is used to determine the extent of the frustration in a material. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f< 10} , then the material is said to be frustrated.

Degenerate ground states means that instead of a ground state characterized by a single potential like in a ferromagnet, it is composed of many potential wells of various depths and this is though to lead to the strange properties exhibited by these materials. Small fluctuations, such as fluctuation in energy allowed by the Heisenberg uncertainty principle, could mean a transition from one ground state to another ground state.

Figure 1. The configuration of spins on a triangle does not allow for all interaction to be satisfied. The left most spin can align up or down to compensate for its neighbor to the right or left but it cannot compensate for both spins at the same time

Figure 2. Four Ising spins on a tetrahedral lattice. Not all spins can align antiferromagnetically because they are arranged on the vertices of a tetrahedra. The bottom right most spin interaction is satisfied but not the left most spin interaction.

Water Ice

Water ice was the first geometrically frustrated material to be studied. In 1936 Giaugue and Stout published The Entropy of Water and the Third Law of Thermodynamics where they reported that water ice has a residual entropy. To find this, they first measured the heat capacity of water from the liquid state through the ice state in a calorimetry experiment. Then they integrated the results and added in the contributions from latent heat to find the entropy. The entropy in the limit of zero Kelvin was found by extrapolating the low temperature values to zero Kelvin.

Figure 3. The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_2O} molecule has a bent shape and this causes ice crystals to form tetrahedras.

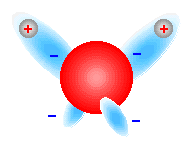
The crystal structure of ice can be directly mapped onto a tetrahedra where there is an oxygen atom at each vertice. Because of the shape of the ice crystal, the hydrogen atoms can arrange in six different ways in the lowest energy state while still maintaining the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_2O } molecule. It is interesting to note why ice crystallizes into a tetrahedral pattern. First of all, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_2O} molecule has a bent shape because the electrons about the oxygen atom arrange in such a way as to increase their distance from each other, minimizing their mutual repulsion. Since there are four electrons, two from the covenant bond with hydrogen, the hydrogen atoms must bond at an angle less than 180 degrees (see Fig. 3). Now to form an ice crystal, the positively charged hydrogen atoms bond to the negatively charged part of the oxygen atom and each oxygen atom is linked through a combination of covalent and hydrogen bonds (see Fig. 4). The bent shape of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_2O} molecule make this possible through sets of repeating tetrahedras (see Fig. 5). The hydrogens are randomly distributed through the ice lattice and are only constraint to the following two rules: 1. there is only one hydrogen per oxygen-oxygen bond and 2. there must be two hydrogens associated with each oxygen. At high temperatures, the hydrogens constantly rearrange to try and satisfy the above rules. As the temperature is decreased, they hydrogens cannot rearrange as quickly and when the temperature is decreased enough, the hygrogens become 'frozen' in a disordered state. Water ice cannot order at low temperatures and is thus frustrated.

Figure 4. Ice crystallizes in a tetrahedra shape where there are six way of arranging the hydogen atoms about the oxygen atom.

Figure 5. Ice crystals forms a repeating tetrhedra pattern. Geometric frustration arises because of the competition between the constraints the ice crystal imposes on the configuration of hydrogens and the rules by which the hydrogens would like to order.

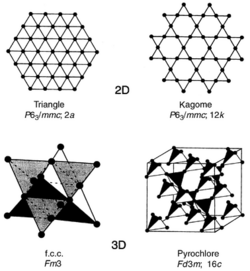
Types of Frustrated Lattices

Each of these crystal lattices are composed of a pattern of triangles and this is the crux of the frustration. Materials that are most likely to exhibit geometric frustration have a triangle based lattice and have short-range antiferromagnetic ordering. This list does not describe all GF latices, however most GF lattices can be understood in terms of the following.

Figure 3. These lattices are all composed of triangles with spins located at the black dots. Because of the structure, these lattices are frustrated when nearest neighbor antiferromagnetic interactions are present.

Triangle

This is also referred to as the Heisenberg triangle and is a two dimensional lattice. Because of its simplicity, the triangle lattice is the subject to much theoretical study, however there have been few experimental investigations. One experimental investigation focus on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Mn_2(THFTC)(H_2O)_3} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle THFTC} is tetrahydrofuran-2,3,4,5-tetracarboxylate. In this case, the lattice is a permutation of the two dimensional triangle lattice into a two dimensional pentagon-triangle pattern and seems to have no long range order down to 1.8 K.

Kagome

Kagome lattice is two dimensional and the name is derived from a Japanese basket-weaving pattern because of its resemblance. Its nominal composition is of the chemical form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AFe_3(SO_4)_2(OH)_6} where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} -site can be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Na^+} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K^+} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Rb^+} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ag^+} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Tl^+} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/2Pb^+} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NH_4^+} , or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_3O^+} . Some substitutions for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Fe^+} can be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/2Hg^{2+}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Cr^{3+}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle In^{3+}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Al^{3+}} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ga^{3+}} . The crystal structure is characterized by a corner-sharing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle FeO_6} octahedra pattern making triangular and hexagonal holes in the lattice. Kagomes are some of the most GF materials and they do not have unique ground state. Some examples are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (D_3O)Fe(SO_4)_2(OD)_6} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle KFe_3(SO_4)_2(OH)_6} .

Pryochlore

The pryochlores are of the chemical form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_2B_2O_7} where the electronic spins are on the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} -sites. Usually the A site is filled by a trivalent rare earth ion and the B site is filled by a tetravalent transition metal. It is important to note that sometimes it is useful to write the chemical formula as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_2O(B_2O_6)} because there exists two independent sublattices, that is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_2O} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_2O_6} The crystal structure is characterized by a three dimensional corner-sharing tetrahedral pattern. Some examples are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Pr_2Zr_2O_7} where the magnetic ion is located on the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} -site and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_2Mn_2O_7} where the magnetic ion is located on the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} -site.

A sublattice of the pryochlore lattice is the spindle which is of the chemical form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB_2O_4} . The main difference is that the crystal structure is characterized by edge-sharing, not corner-sharing, tetrahedral pattern. The consequence of this is that the distance between the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} sites is much shorter than that of the pryochlores and nearest neighbor interactions diminish. As a result spindles often exhibit long range order with complex ground states. Some examples are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle GeCo_2O_4} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle GeNi_2O_4} .

FCC

The FCC (face centered cubic) lattice is the analog of the triangle lattice in three dimensions. The crystal structure is characterized by an edge-sharing tetrahedral pattern.

Characterization

To experimentally study frustrated systems, one looks for singularities or critical temperatures in such bulk probes as heat capacity and magnetic susceptibility. The Heat capacity of a material is useful because from that entropy can be easily calculated and entropy is a gauge of the disorder in a system. It is interesting to know how to entropy approaches zero in the limit of zero Kelvin because from that, one gains information on how the system orders. According to the Third Law of Thermodynamics, entropy is zero at zero Kelvin, but as mentioned for water ice, in frustrated systems the entropy tends to a finite value in the limit of zero Kevin. This is a common characteristic of geometrically frustrated materials and is thought to arise from the fact that there exists degenerate ground states.

Figure . Magnetic susceptibility for frustrated materials. The signature is that the ordering temperature is much greater than the Curie-Weiss temperature.

Figure . Magnetic susceptibility for nonfrustrated materials. Here the ordering temperature is of the order of the Curie-Weiss temperature.

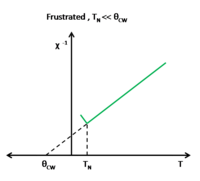
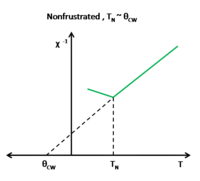
Another characteristic of frustration is the inverse of the magnetic susceptibility curve. In antiferromagneitc nonfrustrated systems the ordering temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_N=\theta_{CW}} where for antiferromagnetic frustrated systems Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_N<<\theta_{CW}} (See Fig. ). It is common in experimental analysis to extract the exchange interaction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J} and the Curie-Wiess temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{CW}} . To do this, at high temperatures the magnetic susceptibility data is fit to the inverse of the Curie-Weiss Law, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi^{-1}=\frac{T-\theta_{CW}}{C}} , where the slope is the reciprocal of the Curie constant, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} and the intercept is the ratio of the ordering temperature and Curie constant, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\theta_{CW}}{C}} , and so the Curie-Weiss temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{CW}} can easily be determined. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{CW}} will diverge to negative values if the spin interaction is antiferromagnetic and the extracted $\theta _{CW}$ will be negative. $\theta _{CW}$ will diverge to positive values if the spin interaction is ferromagnetic and the extracted $\theta _{CW}$ will be positive.

X-ray diffraction is commonly used in crystallography to determine the structure of a material. In this case, x-ray diffraction can be used as a smoking gun in order to identify a geometrically frustrated material by comparing the diffraction pattern to those of frustrated lattices described above because the nature of this problem is the crystal structure.

Figure . X-ray diffraction pattern for a pryochlore lattice. The purple line below is the subtracted background data and the red line is the data that is used to compare against a known pryochlore diffraction pattern in black. The vertical lines represent the brag peaks or the location of the atoms in the lattice.

When the material of interest is frustrated because of magnetic interactions, it is important to prob the magnetic structure. To do this, scientists use a technique called neutron scattering. Neutrons are a powerful tool to probe magnetic behavior because they are neutral and do not interact the electronic spins in the material. The scattering relation (analogous to Bragg's Law for x-ray diffraction) has been estimated by taking the potential energy of the neutron in the magnetic field of the electron as a perturbation. In this system, the magnetic moment of an atom is described by a contribution of $b_{m}=psin(\alpha )$, to the neutron scattering length, where $\alpha$ is the angle between the magnetic moment and the scattering vector.

Ground States

Geometrically frustrated materials have many ground states and it is important to look into this a bit more in order to understand if and how these materials order into some lowest energy state.

Long Range Order

Long range order means that the interactions in a material is globally in equilibrium and this state is usually achieved by a phase transition like a transition from a paramagnetic state to and antiferromagnetic state . Long range order is usually achieved in non-frustrated materials (the 3D Ising Model). The presences of frustration complicates the situation. Frustrated materials that do have long range order form what is called a compromised spin configuration where if the spin interaction is antiferromagnetic on a tetrahedral lattice for instance, the spins will align pointing outward at and angle of 109 degrees.

Cooperative Paramagnets

Many frustrated materials do not go through a phase transition to a long range ordered state and their spins remain dynamic down to zero Kelvin. That means that the magnetic moments of the material continues to fluctuate for all temperatures. This behavior has been observed especially in the pryochlore lattice where separately each tetrahedral may have two pairs of antialigned spins (for antiferromagneitc interaction) and would be in a ground state, but globally there is no correlation between the tetrahedrals. because of this there is a very large number of lowest energy states, separated by a small amount of energy, and there is no unique long ranged ordered state.

Spin Glass

The spin glass state is characterized by spins "frozen" in random directions with a small energy difference separating one possible random state from the next. What happens here is that there exists a freezing temperature, $T_{f}$, or glass transition temperature, $T_{g}$, where the material goes through a phase transition where the previously randomly fluctuating spins become frozen in what ever direction they find themselves in at the point of the phase transition. It is obvious that there is a lack of long range order.

Spin Liquid and Spin Ice

Spin liquid and spin ice states are subsets of the cooperative paramagnetic states. The spin liquid state is rarely observed and occurs when there is no spin freezing temperature$T_{f}$. The spins, or a large fraction of the spins still fluctuate all the way down to zero Kelvin. The spin ice state is a special case of the spin liquid where Ising spins are arranged on a pryochlore (tetrahedral) lattice. These care called spin ices because this problem maps directly onto the water ice problem described above.

Why should geometric frustration be studied and what are possible applications?

As the story goes, when Rutherford had requested support for his study of the electron, his potential benefactors asked him why they should help him and what the electron can be used for. Rutherford replied by professing that he didn't know. It is evident today that electrons are useful in many ways like the treatment of tumors with radiation therapy and atomic imaging the surfaces of solids with a scanning tunneling microscope. These are applications that Rutherford may not have ever imagined and so by analogy, the applications of geometrically frustrated materials are most likely wide and varied but unknown and possibly unimaginable today.

The more realistic answer is that geometric frustration is the subject of intense investigation because it seems to be a fundamental problem that appears in nature. Water ice, as mentioned above, is not an exotic state of matter and exhibits frustration in the ordering of protons. It appears that at low enough temperatures, the proton order is randomly 'frozen' in. It has been proposed that there may be some fundamental physics that govern the way materials order that has been previously overlooked. There is reason to believe that this is true because of the characteristic residual entropy in frustrated materials. Scientists have formulated the laws of thermodynamics some what based on the assumption that there exists a single ground state, which is not the case of geometrically frustrated materials. Maybe the third law of thermodynamics needs to be revised to state that the entropy must saturate to a finite value, instead of just zero Kelvin, or it must be understood that the third law does not apply.

Figure . Smart bionanotubes. Lipid protein nanotubes made of microtuble protein that could aid in drug delivery.

Liposomes are an example of a geometrically frustrated material where the exchange interaction is more significant than that imposed by the lattice so that the lattice actually deforms into a space enclosing ball as a response to the frustration. This self-deformation property is useful in textiles, cosmetics, and drug delivery. For example, nanotubules are a variation of liposomes and its self-assembling process is useful to target small parts of the body for administration of small amounts of drugs. By understanding geometric frustration better, the size and shape of nanotubes can be better refined and can have more diverse applications in drug design.

References

John E. Greedan. Geometrically frustrated magnetic materials, Journal of Materials Chemistry, 2001, Vol. 11, pg. 37-53, http://www.rsc.org/publishing/journals/JM/article.asp?doi=b003682j

A. P. Ramirez. Strongly Geometrically Frustrated Magnets, Annual Reviews Materials Science, 1994, Vol. 24, pg. 453-480, http://arjournals.annualreviews.org/action/doSearch?action=runSearch&type=advanced&result=true&prevSearch=%2Bauthorsfield%3A(Ramirez%2C+A+P)

A. P. Ramirez. Geometric frustration: Magic moments, Nature, 2003 Vol. 421, pg. 483, http://www.nature.com/nature/journal/v421/n6922/full/421483a.html

Geometrical Frustration, http://en.wikipedia.org/wiki/Geometrical_frustration

Mark Harris. Taking the frustration out of ice, http://www.physics.rutgers.edu/~pchandra/physics681/frustration_outof_ice.pdf

Hydrogen Disorder in Ice, http://www.physicsofmatter.com/NotTheBook/Talks/Ice/Ice.html

'Smart' Bio-nanotubes Developed; May Help in Drug Delivery, UCBS Press Release, 2005, http://www.ia.ucsb.edu/pa/display.aspx?pkey=1325

J. R. Hook and H. E. Hall. Solid State Physics