Homeworks 1

Homeworks 1

Homeworks 1 About this Assignment Topics Sizes Algebra Conversion Solar Systems Elliptical orbits Chapters 1 - 2 Lectures 2 - 4

Homeworks 1 is the attempted solution to our second task in the course Introduction to Astrophysics. This assignment is due on Wednesday 09/09/09 and was assigned on 09/01/09. Solutions were created by Group 1 (RyanT, KimW, SaraC, ZackM, TiaraD) to be completed by 09/11/09.

This assignment covers Chapter 1 and 2 in the book, Lectures 2 through 4. The topics in this assignment range from sizes, to solar systems, to why the orbits of the planets are elliptical.

Problem 1

List in order of increasing size and give the approximate size of the following objects: An atom, a biological cell, a cluster of galaxies, the Earth, a galaxy, the Local Group of galaxies, a neutron, a neutron star, a person, the Solar System, our sun. Note: you may have to look in other books besides your textbook to get all this information.

There are 3 ways to approach this problem: By radius, by volume, and by mass.

This problem coincides with Lecture #2. 

By Radius

1. Neutron = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3 quarks \;} (or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r \approx 1.11 \times 10^{-15} m \;} )
2. Atom's empirical atomic radius Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 0.62 - 5.20 \times 10^{-10} m \;}
3. Biological Cell Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 1.00 \times 10^{-5} m}
4. Human's height Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 1.50 m \;}
5. Neutron Star Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 1.20 \times 10^4 m \;}
6. Earth = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6.38 \times 10^6 m \;}
7. Sun = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6.96 \times 10^8 m \;}
8. Solar System
   1. Radius of the farthest comet's orbit (Oort Cloud) = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 7.50 \times 10^{15} m \;}
   2. Distance from the Sun to Jupiter = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 7.48 \times 10^{11} m}
9. Galaxy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 5 \times 10^4 ly \;} = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4.73 \times 10^{20} m \;}
10. Local Group of Galaxies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 5 \times 10^6 ly \;} = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4.73 \times 10^{22} m \;}
11. Cluster of Galaxies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 5 Mpc \;} = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1.54 \times 10^{23} m}

By Volume

1. Neutron Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=(1 fm)^3=10^{-45} m^3 \;}
2. Atom Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=(10^{-9} m)^3=10^{-27} m^3 \;}
3. Biological cellFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=(10^{-6} m)^3=10^{-18} m^3 \;}
4. Human Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=(2m)^3=8 m^3 \;}
5. Neutron Star Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V= \tfrac{4}{3} \pi (12 \times 10^3 m)^3=8\times 10^{10} m^3 \;}
6. Earth Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=\tfrac{4}{3} \pi (6 \times 10^6 m)^3=10^{21} m^3 \;}
7. Solar System Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=(4\times10^{12})^3=64 \times 10^{36} m^3 \;}
8. Galaxy (contains many star systems)
9. Local group of galaxies (contains many galaxies)
10. Galaxy Cluster (contains many groups of groups of galaxies, larger than local group)

By Mass

1. Neutron = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1.67492729\times10^{-27} \;} kg
2. Atom = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1.67 \times 10^{−27} \;} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4.52\times10^{−25} kg \;}
3. Biological cell = varies (eukaryotic cells are more massive than prokaryotic cells)
4. Human = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 76^{-83} kg \;} for males (average) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 54-64kg \;} for females (average)
5. Earth = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5.9736 \times 10^{24} kg \;}
6. Sun = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1.9891 \times 10^{30} kg \;}
7. Solar System = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1.991768 \times 10^{30} kg \;} (excluding Asteroid Belt, Kuiper Belt, and comets)
8. Neutron star = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2.69 \times 10^{30} \;} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4.177 \times 10^{30} kg \;} (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1.35 \;} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2.1 M_{\odot} \;} )
9. Galaxy = varies (Milky Way is approximately Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5.8 \times 10^{11} M_{\odot}\;} )
10. Local Group = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1.29 \pm 0.14) \times 10^{12} M_{\odot} \;}
11. Galactic cluster = varies; usually approximately Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{13} M_{\odot}\;}

Problem 2

The nearest star outside the solar system is about 4 light years away.

1. How far away is the star in kilometers?

   One light year is approximately Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 9.460730472 \times 10^{15} m} .

   Therefore, this star is approximately Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3.784 \times 10^{13} km} .

2. Suppose you travel to the nearest star in a rocket ship moving at 100 km per hour (100 km/hr is about 62 mi/hr, a typical automobile speed on a Florida highway). How many years will it take you to get to the star?

   Knowing the distance of this star in kilometers, one can find the time it takes to get there with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = \tfrac{d}{v}} .

   Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = \frac{3.784 \times 10^{13}km}{\tfrac{100km}{hr}} = 3.784 \times 10^{11} hrs} .

   This equates to about 43,196,347 years!

3. Suppose you travel to the star at 10 km per second (the speed of a rocket in orbit around the Earth). How many years will it take you to get to the star?

   Again, use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = \tfrac{d}{v}} , but with time in seconds

   Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = \frac{3.784 \times 10^{13}km}{10\tfrac{km}{s}} = 3.784 \times 10^{12} s} .

   This equates to about 120,000 years!

Problem 3

Use the size of the Astronomical Unit in kilometers and the length of the year in seconds to calculate how fast the Earth moves in its orbit in kilometers/second.

The speed of Earth in its orbit around the sun can be determined from the total distance it travels in a certain time period. For convenience, in one year, the Earth has completed one revolution about the sun (or the circumference of a circle with radius 1AU).

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |v| &=\frac{l}{t}\\ &=\frac{2\pi\times1AU}{1yr}\\ &=2\pi\frac{AU}{yr}\times\frac{1.5\times10^8km}{1AU}\times\frac{1yr}{365.25days}\times\frac{1day}{24hr}\times\frac{1hr}{3600s}\\ &=30\frac{km}{s}\\ \end{align} }

Therefore, the speed of Earth in its orbit is approximately 30km/s.

Problem 4

Describe the essential differences between the Ptolemaic, Copernican, and Keplerian descriptions of planetary motion.

The Ptolemaic description of planetary motion was that of a geocentric solar system in which all planets and the sun orbit the earth. Ptolemy also described the retrograde motion of the planets and moon using epicycles.

Copernicus introduced the heliocentric model of the solar system in which all planets orbit the sun. Copernicus also explained that the apparent retrograde motion of the planets and moon is actually a result of the earth's motion.

Kepler maintained the heliocentric model of planetary motion and introduced that planets move in elliptical orbits about the sun with his idea of conic sections.

Problem 5

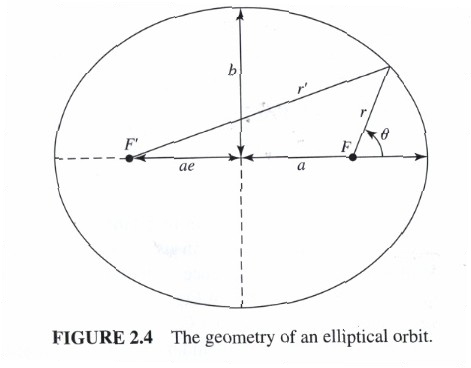
Use Newton’s laws to show that the orbits of planets are ellipses.

Kepler's First Law is that the orbits of our planets are ellipses (with the sun at one focal point). However it does not explain why the planets move as they do in elliptical loops. Therefore, this question can be restated: Use Newton's laws to derive Kepler's First Law.

This problem coincides with Chapter 2.3 Kepler's Laws Derived and Lecture #4. 

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a \;} = semimajor axis

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b \;} = semiminor axis

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textbf{r} \;} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textbf{{r}'} \;} = distances to focal points

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textbf{F} \;} and ${\textbf {{F}'}}\;$ = focal points

$e={\frac {\left|F-{F}'\right|}{2a}}\;$ = eccentricity

This problem is incomplete.

The Equation for an Ellipse is $r+{r}'=2a\;$, and in polar coordinates

$r={\frac {a(1-e^{2})}{1+e\cos \theta }}\;$ for $0\leq e<1$

Conservation of Angular Momentum ${\textbf {L}}\;$

${\textbf {L}}=m_{1}{\textbf {r}}_{1}\times {\textbf {v}}_{1}+m_{2}{\textbf {r}}_{2}\times {\textbf {v}}_{2}\;$

Define Reduced Mass $\mu \;$

$\mu \equiv {\frac {m_{1}m_{2}}{m_{1}+m_{2}}}\;$

Total Angular Momentum ${\textbf {L}}\;$ with respect to Reduced Mass $\mu \;$

${\textbf {L}}=\mu \cdot {\textbf {r}}\times {\textbf {v}}\;$

With reduced mass $\mu \;$ (and because of it), total angular momentum ${\textbf {L}}\;$ is constant.

${\frac {d{\textbf {L}}}{dt}}=0\;$

Kepler's 1st Law

$r={\frac {\tfrac {L^{2}}{\mu ^{2}}}{GM(1+e\cos \theta )}}\;$

References

• B.W. Carroll & D. A. Ostlie (2007). An Introduction to Modern Astrophysics (Chapter 2). Addison Wesley. ISBN 0-8053-0402-9
• Lecture #2
• Lecture #3
• Lecture #4