Homeworks 3

Homework 3 due on 09/21/2009

Problem 1

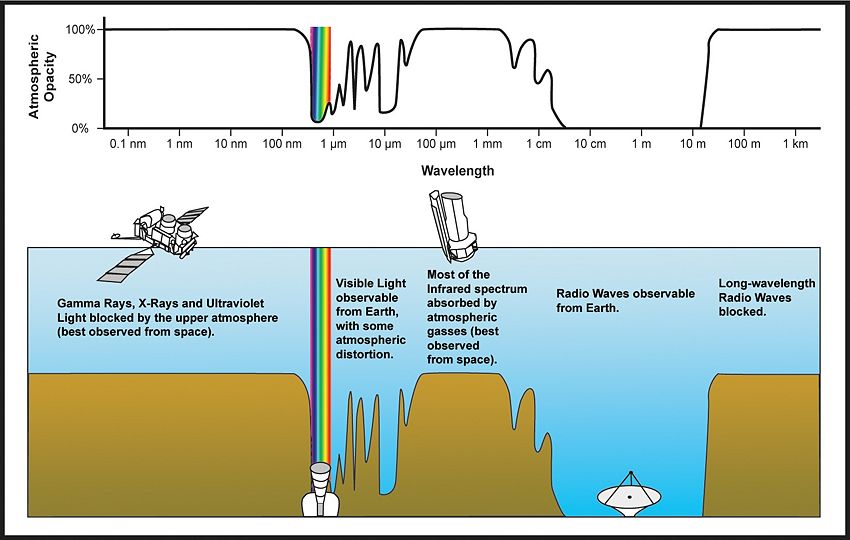
For each of the following types of electromagnetic radiation give a typical wavelength and state whether it can penetrate the Earth’s atmosphere: radio, microwave, infrared, visible, ultraviolet, X-ray, $\gamma$-ray.

A visual image of the electromagnetic windows through Earth's Atmosphere.

Typical Wavelength and Atmosphere Penetration

Wavelength	Wavelength Range	Does it penetrate Earth's Atmosphere?
Radio	10 m - $10^{8}$ m	From ~10 m to ~20 m, yes
Microwave	$10^{-3}$ m - 10 m	Some is absorbed at smaller wavelengths
Infrared	700 nm - $10^{-3}$ m	Most are absorbed by atmospheric gasses
Visable	400 nm - 700 nm	Yes, with some distortion
Ultraviolet	$10^{-8}$ m - 400 nm	No, all incoming rays are blocked
X-Ray	$10^{-11}$ m - $10^{-8}$ m	No, all incoming rays are blocked
$\gamma$-ray	$10^{-17}$ m - $10^{-11}$ m	No, all incoming rays are blocked

Problem 2

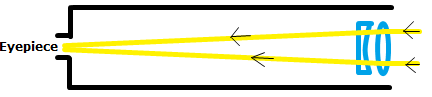
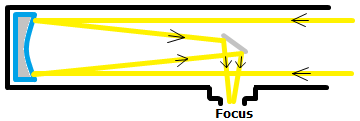
Sketch the typical light path of reflector and refractor telescopes, and name two of the advantages and disadvantages for each of the designs. Catadioptric designs such as the Maksukov and Schmidt telescopes have both a primary lense and a mirror. Name the main advantage and drawback of these designs, and their main application.

Refraction Telescope

The light path of a typical refraction telescope.

Advantages and Disadvantages of Refraction Telescopes

Advantages	Disadvantages
High resolution	Large objective lenses deform under gravity.
No incoming light is blocked.	Chromatic aberration

Reflection Telescope

The light path of a typical reflection telescope.

Advantages and Disadvantages of Reflection Telescopes

Advantages	Disadvantages
No chromatic aberration	The prime focus is in the path of incoming light.
Only the reflecting surface needs to be polished to perfection.	Large detectors produce a lot of torque.

Catadioptric Telescope

Catadioptric telescopes like the Schmidt telescope provide a wide-angle field of view and thus are often used as cameras. They can designed for wide field views because two more surfaces allow higher order corrections. However, they suffer from both spherical and chromatic aberration.

Problem 3

Name and explain in your own words three of the optical artifacts of spherical mirrors. Explain why telescopes with multiple-mirrors such as Keck or the upcoming space based NGST are inferior for direct imaging of planets compared to mono-mirror systems. Why, then, are all large telescope systems are based on multiple mirror designs?

Spherical mirrors suffer from several types of optical artifacts. Coma is an effect that causes point sources to appear elongated. Astigmatism occurs when an image is focused onto slightly different points on the focal plane. Curvature of field occurs due to the fact that images are focused on a curve rather than on a plane.

Telescopes with multiple mirrors are inferior for direct imaging of planets because of the signal noise induced by the edges of the mirrors. However, most large telescopes continue to use multi-mirror designs since it is much easier to support several small mirrors rather than one large mirror.

Problem 4

Use the Rayleigh Criterion to estimate the diffraction limit (in arc sec) for the angular resolution of a typical 1m class telescope in the near IR (2 μm), and discuss the result.

The Rayleigh Criteron: $\theta \thickapprox 1.22{\frac {\lambda }{D}}$

$\lambda =2\times 10^{-6}m$

$D=1m$

We plug in these values and we get that:

$\theta \thickapprox 1.22{\frac {2\times 10^{-6}m}{1m}}=2.44\times 10^{-6}rad=1.398\times 10^{-4}deg=0.503arcseconds$

Problem 5

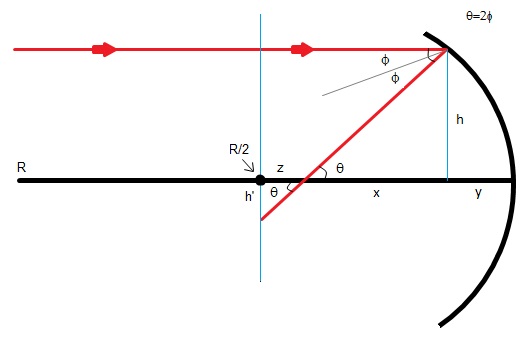
Estimate the size of the spherical aberration of a spherical mirror of 1m-diameter and a focal length of 2 meter. (Hint: Calculate the size of the smeared image of a star at the focal point and compare it to the size (in arc-sec) of an extended object, and remember your PHY2048/9).

The diagram has been exaggerated to show the geometric relations.

We all know that for small angles,

$f={\frac {R}{2}}$

Where f is the focal length and R is the radius of curvature for a spherical mirror. The problem is that with large angles, the foci will not match up, causing the aberration.

For large angles, the focal length can be written as, $f'=x+y$ and the angles can be determined directly through trigonometric relations from the diagram. They are,

$\cos {\phi }={\frac {R-y}{R}}$ and $\tan {\theta }={\frac {h}{x}}$.

Where h is the height from the incoming light ray when the light ray strikes the mirror, to the optical axis. Solving for x and y in both of these equations, the focal length becomes,

$f'={\frac {h}{\tan {\theta }}}+R-R\cos {\phi }$

Here I define, $\theta =2\phi$, so the focal length becomes,

$f'={\frac {h}{\tan {2\phi }}}+R-R\cos {\phi }$.

Next, I define my aberration to be some variable, z. z is the horizontal distance on the optical axis between the foci. The small angle focus is at R/2 and the large angle focus occurs at the focal length f'. Therefore,

$z={\frac {R}{2}}-f'$

Thus, plugging in our known value of f', z becomes,

$z={\frac {R}{2}}-{\frac {h}{\tan {2\phi }}}-R+R\cos {\phi }.$

Using double angle formulas, and trigonometry, the angles may be parametrized out of the equation, making z only in terms of R and h. Eventually, after a little bit of tedium, z becomes,

$z={\sqrt {R^{2}+h^{2}}}-{\frac {R^{2}-2h^{2}}{2{\sqrt {R^{2}-h^{2}}}}}-{\frac {R}{2}}$

This z is one of the ways to calculate the size of the spherical aberration, but it is dependent on h. Normally we know things like the focal length and the radius of curvature so I cannot directly find the numerical value of the aberration, but derivation of a similar equation based on the horizontal distance h' from R/2 to the reflected light ray being dependent on the focal length would give a value given our constants.

Also, just as check, it can easily be seen that in the limit as $h->0$, z reduces to the expected result of zero.

$z={\sqrt {R^{2}+0}}-{\frac {R^{2}-0}{2{\sqrt {R^{2}-0}}}}-{\frac {R}{2}}$

$z=R-{\frac {R^{2}}{2R}}-{\frac {R}{2}}$

$z=R-{\frac {R}{2}}-{\frac {R}{2}}=0$