PHZ3400-09 Problem Set 1

Problem 1

a) Briefly describe how the study of blackbody radiation led to Planck’s quantum hypothesis.

b) Derive Wien’s law from Planck’s radiation formula.

c) Derive the Stefan-Boltzmann law from Planck’s radiation formula.

Use: $\int _{o}^{\infty }[x^{3}/[e^{x}-1]dx=\pi ^{4}/15.$

Problem 2

a) Derive a (non-relativistic) expression for the de Broglie wavelength (in nanometers) of an electron in terms of the potential difference V (in volts) through which it has been accelerated.

b) A scanning electron microscope (SEM) uses an electron beam of energy of 30 keV. What is the smallest feature that can possibly be resolved with this SEM?

c) Estimate the de Broglie wavelength of yourself when you are walking at a brisk pace. Discuss the result.

Problem 3

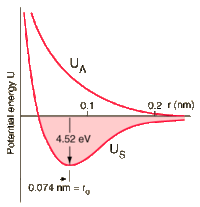
Suppose that the interaction energy between two atoms is given by:

$E(R)=-{\frac {A}{R^{2}}}+{\frac {B}{R^{10}}}$

The atoms form a stable molecule with an inter- nuclear distance of 0.3nm and a dissociation energy of 4 eV.

a) Determine A and B.

b) Calculate the force required to break the molecule. What is the critical distance between the nuclei for which this occurs?

Problem 4

In class, you were given a brief overview of different types of chemical bonding. A simplest example of a chemical bond is that formed by two hydrogen atoms in a $H_{2}$ molecule.

a) Provide a quantum-mechanical description of the electronic states for this molecule, the bonding and the anti-bonding orbital.

b) Show that in the ground state (both electrons in the bonding orbital), the molecular energy has a minimum at a finite distance $r_{o}\approx 0.074nm$, defining the bond length for $H_{2}$.

c) Determine the energy needed to break this bond.

I realize that a full and rigorous mathematical solution to the problem of covalent bonding requires a level of familiarity with Quantum Mechanics (QM), which may be beyond what is normally described as "Modern Physics". Some people in this class may have had more advanced QM training, and these are invited to provide a more rigorous solution of this problem, using for example Huckel theory (i.e. the "tight binding" method; also called "linear combination of atomic orbitals"). Others may provide a more heuristic description of covalent bonding, akin to that found in many Modern Physics or Introductory Chemistry texts. These often use arguments based on the Heisenberg Uncertainty Principle to estimate the optimum bond length for covalent bonds, and their binding energies.