PHZ3400 Phase Transition

“ Thin films have quantum transitions, where a superconductor becomes an insulator ”

Group 3 is the best

Phase Transition Snowflake Phases of Matter Phases Solid Liquid Gas Plasma Transitions 1st order Temperature Pressure

A classical phase transition (AKA thermal phase transitions) describes a cusp in the thermodynamic properties of a system. It signals a reorganization of the particles; A typical example is the freezing transition of water describing the transition between liquid and ice. The classical phase transitions are driven by a competition between the energy of a system and the entropy of its thermal fluctuations. At zero temperature, a classical system does not have entropy and therefore no phase transition can occur.

A quantum phase transition is a phase transition between different quantum phases (phases of matter at zero temperature). Contrary to classical phase transitions, quantum phase transitions can only be accessed by varying a physical parameter - such as magnetic field or pressure - at absolute zero temperature. The transition describes an abrupt change in the ground state of a many-body system due to its quantum fluctuations. Such quantum phase transitions can be 1st-order phase transition or continuous 2nd order.

In summary, even at zero temperature a quantum-mechanical system has quantum fluctuations and therefore can still transition into a different phase of matter, unlike classical transitions.

Phases of Matter

Matter can exist in many phases. The phases most common are solids, liquids, and gases. In Physics, a phase can be described as a region of space in which all physical properties of a material remain constant, or uniform. Having consistent physical properties and chemical uniformity allows one to distinguish between the various phases, or states of matter. In terms of entropy, we can also define the state of equilibrium for matter. There are three basic states:

• Stable - A system in which a phase separation would cause an increase in the free energy. This phase separation doesn't happen naturally, so the system is stable and doesn't change.

• Unstable - A system in which a phase separation causes a decrease in the free energy. This process will happen at any small fluctuation in the system, so the system is very unstable and usually changes immediately.

• Metastable - The system is stable with respect to small fluctuations in the matter, but will phase separate with larger fluctuations. This system has an energy barrier which needs to be overcome in order for these phases to separate.

Soft Matter

Soft matter is very complicated matter. What is remarkable about soft matter is its ability to put itself into complicated arrangements, all without outside assistance. This is known as self-assembling. There are two ways to classify self-assembled structures: at equilibrium or non-equilibrium, which are structures that are a result of a phase change. Soft matter often shows rather complex equilibrium phases.

Phase Transitions

After a phase transition, a self-assembled structure is at non-equilibrium. These phase transitions usually result in a less ordered state, which can be shown through liquids and solids; liquids are less ordered than solids. They characterize these phase transitions, they are ordered, which is based on the nature of the transition.

First - Order

A first-order phase transition is where order parameters (such as temperature and energy) changes discontinuously at the phase transition.

This kind of phase transition represents crossing a boundary between phases on a phase diagram. This type of transition differs from a second-order phase transition where order parameters change continuously. This uniformity of a second-order phase transition is well represented in the change from a liquid to a gas around its critical point. Instead of directly crossing the boundary from liquid to gas, the liquid can be pressurized to exceed the pressure of the critical point, then heated to exceed the temperature of the critical point, and finally depressurized and cooled to a gas in a continuous change of phase.

Second - Order

In a second-order phase transition, order parameters (such as temperature and energy) remain continuous. This uniformity of a second-order phase transition is well represented in the change from a liquid to a gas at its critical point. This type of transition is also important for ferromagnets and superconductors.

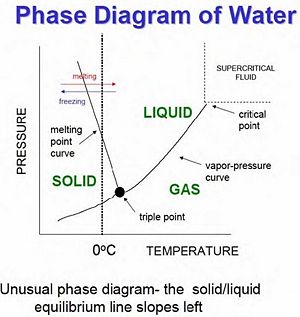
Gas-Liquid-Solid Phase Diagram

Phase Diagram of Water

When studying phase transitions, it is important to be able to read and understand a phase diagram. A phase diagram is a pressure vs. temperature graph of an element or compound that shows which phase we can expect it to be in (see right for example). The lines represent the boundaries between phases, and at any point on these lines we can expect two (or even three) phases to exist simultaneously in equilibrium. In the area between curves only one phase of matter exist. There are two important points on phase diagrams which should be mentioned:

Triple Point - At this specific temperature and corresponding pressure, the three phases of matter can exist simultaneously in equilibrium. This means that evaporation, condensation, freezing, melting, fusion, and sublimation are happening at once.

Critical Point - At this point in temperature and pressure (and at any point above this), the boundary between liquid and gas doesn't exist any more. Here a gas cannot be distinguished from a liquid, and the heat of vaporization is zero. However, you can still have a smooth transition between gas and liquid by going up and around the critical point (as seen on the phase diagram) by passing through the supercritical fluid region.

Phase Separation and Nucleation

When a fluid is in the co-existence dome of a phase diagram, phase separation occurs. This happens because the density of the fluid is in between that of a liquid and that of a gas, so both phases exist at once (hence the name co-existence dome). Phase separation occurs because of a continuous change in composition, which is done by a process known as spinodal decomposition. In spinodal decomposition, any small changes made in composition are amplified as a result of the free energy being lowered. This also is a result of the system being unstable.

Nucleation: is the process where gas begins to condense to form liquid droplets, but both co-exist at the same time. Usually there will be a global phase separation, where the gas and liquid separate out completely. But when dealing with charged particles charge neutrality forbids this, so instead nano-scale phase separation occurs where the two phases do not completely separate, but droplets form. The energy domain of the wall of these droplets (E) is dependent on the surface area and volume of the droplet formed:

$E=\sigma S(t)-2hV(t)$,

where $\sigma$ is the surface tension, S(t) is the surface area with respect to time, h is a small chemical potential, and V(t)is the volume with respect to time. The sphere is geometrically the most efficient shape for the droplet to be in be in because it minimizes the area of interface between the two drops, and in nature this is the shape that the droplet takes. Substituting the surface area and volume of a sphere into the equation, we get:

Graph of Critical Droplet Size

$E=\sigma 4\pi R^{2}-{\frac {8\pi }{3}}hR^{2}$

Taking the derivative and setting it equal to zero, we can find the maximum (critical) droplet size:

$R_{c}=\sigma /h$

Therefore, the radius of the critical droplet is dependent on the surface tension of the droplet and the chemical potential of the material. If $R>R_{c}$ the droplet will grow (nucleation and growth), and if $R<R_{c}$ the droplet will shrink. The probability of any particle nucleating is proportional to the Boltzmann factor, that is:

$P\sim e^{\frac {E}{k_{B}T}}$

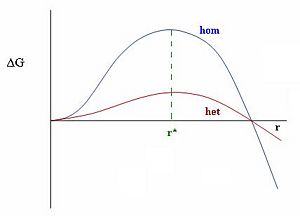
Looking at the graph on the left one can see the large energy difference between heterogeneous and homogeneous nucleation. A state without any impurities requires a lot of energy to overcome the energy barrier before nucleation. This helps to explain how we can have "supercooled" water in the atmosphere, tiny water droplets which can be much colder than their usual freezing point of zero degrees Celsius. Adding tiny particles, such as dust or "seeds" for inducing cloud precipitation, lowers the surface tension required by the droplet because it can use these particles as surfaces with which to nucleate. As the surface tension decreases, both the critical radius of the droplet and the energy required to form it decrease.

This relates the energy E to the radius R of the droplet. We can see from this equation that as R is small the first term dominates, and as R becomes very large the second term dominates. By taking the derivative of this equation and setting it equal to zero we can find the maximum of this function, which physically represents the critical droplet size of nucleation.

Vlad: You need to include ALL the derivations I presented in class, when preparing these lecture notes!!! Please do it promptly

Density

Why does ice float? An object will float if it is less dense than the fluid that it has been placed in. For an object of mass m to float, it must displace mass m of liquid.

Water reaches its maximum density at 4 degrees C and then continues to freeze. When it freezes, the solid ice is less dense than the liquid water. Usually, the liquid state of a material is less dense than the solid. The difference in the case of water is hydrogen bonding.

{{#ev:youtube|gmjLXrMaFTg}}

The water molecule is composed of two hydrogen atoms and one oxygen atom held together by covalent bonds. The molecules have a weak attraction to each other in the form of a hydrogen bond. This occurs between the positively charged hydrogen atoms in the molecule and the negatively charged oxygen atoms in another molecule. When water freezes into a solid, the hydrogen bonds adjust such that the negatively charged oxygen atom in each molecule are far apart. This creates a lattice that is less dense than the liquid form.

Van der Waals Equation

Johannes Diderik van der Waals

Vlad: You need to include ALL the derivations I presented in class, when preparing these lecture notes!!! Please do it promptly

We know that each atom or a molecule in a liquid has a very steep repulsive potential at short distances, due to the Pauli exclusion principle. Thus a volume comparable to the atomic radius is essentially excluded to other particles. This considerably limits the volume of space accessible to thermal motion of every atom or molecule.

Johannes van der Waals incorporated this into his theory. To do this he made two modifications to the ideal gas law,

$PV=NkT\!$

His first modification was to restrict the volume of a molecule by introducing a minimum volume, $Nb$. The constant $b$ then represents the minimum volume occupied by a molecule, when it's "touching" all its neighbors. This modification gives us:

$P(V-Nb)=NkT\!$

Van der Waals second modification to the ideal gas law was to add the term ${\frac {aN^{2}}{V^{2}}}$. This term is the pressure due to the total potential energy, which accounts for the short-range attractive forces between molecules when they are not touching. This second modification gives us Van der Waals Equation:

$(P+{\frac {aN^{2}}{V^{2}}})(V-Nb)=NkT$

$P$ is pressure

$T$ is temperature

$N$ is the number of particles

$V$ is volume of the container containing the fluid

$a$ is the measure of attraction between particles

$b$ is the volume excluded by a mole of particles.

Behavior Near Critical Point

We can derive the behavior of Van der Waals Equation near the critical point to discover how a fluid behaves near the critical point. As we increase $T$ to some critical temperature, $T_{c}$ we find that

$T_{c}={\frac {8}{27}}{\frac {a}{b}}\!$

$V_{c}=3Nb\!$

$P_{c}={\frac {1}{27}}{\frac {a}{b^{2}}}\!$

Using these critical values we can scale Van der Waals Equation to put it in its universal form.

$({\frac {P}{P_{c}}}+3({\frac {V_{c}}{V}})^{2})(3{\frac {V}{V_{c}}}-1)=8{\frac {T}{T_{c}}}\!$

In this form isotherms corresponding to the given scaled temperature would collapse on a single curve. This predicts the universal number:

${\frac {P_{c}V_{c}}{T_{c}}}={\frac {3}{8}}$

Experimental evidence shows that many different fluids have a ratio of 0.3, which is in agreement with the theory.

Sources

• "Soft Condensed Matter", Richard A.L. Jones

• "An Introduction to Thermal Physics", Daniel V. Schroeder