PHZ3400 Sound

Vibrational modes of a one-dimensional chain

Harmonic approximation: inter-atomic forces as springs

If we put energy into a crystal the atoms will begin to vibrate. We are able to put energy into crystals in two different forms, Mechanical and Thermal. Mechanical energy corresponds to sound waves propagating through a solid.

• Thermal energy can be used to measure resistivity.

These problems can be very complicated if we try to take them head on. Luckily however, there are ways in which we can simplify the problem. One aspect that helps to simplify the problem of lattice vibrations is the periodicity of the crystal. Another way we can simplify is to use Hooke's law to treat the inter-atomic forces as springs.

Now let's focus on two particles together with a spring. If we displace each particle with the same force we will get simple sinusoidal motion as in a linear harmonic oscillator. Using this condition we can displace the atoms in two ways, or modes. One way is to displace the particles, so that they are in phase, this can be seen as the center of mass of the system of two particles moving. The second way is to displace the particles out of phase, such that their motion opposes each other. This mode can be seen as the internal vibrations of a molecule.

When the two atoms are moving together they effectively have a larger mass, therefore they will a smaller frequency than when the atoms move out of phase. This follows from

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_0 = \sqrt{\frac{k}{m}}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is the spring constant and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} is the mass of the particle or particles when in phase.

In general though, molecules will not act in such a simple fashion. Usually there will be a superposition of many modes which create a complicated beat pattern.

• Broken Symmetry
• Collective Phenomenon - behavior changes when in a large group

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_2} Example

Consider an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_2} molecule. Assume one is at rest while the other moves. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ma = -\frac{dV(r)}{dr}}

,where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is potential energy and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} is radius. This can be rewritten as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\frac{d^2r}{dt^2} = -\frac{dV(r)}{dr}}

This equation cannot be solved via conventional methods, so we must somehow simplify it. Let us only worry about very small oscillations. This reduces our problem to a harmonic oscillator. Small oscillations can be described simply since it is parabolic at the minimum energy.

Now we expand Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)} in Taylor Series (note Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_0} is the radius with minimum V)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r) = V(r_0) + V'(r_0)(r - r_0) + \frac{1}{2}K(r - r_0)^2}

,where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K = \frac{d^2V}{dt^2}} .Notice that the second term is the derivative of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_0} , which is a minimum, therefore the derivative is zero and this term can be ignored. Now we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r) = V(r_0) + \frac{1}{2}K(r - r_0)^2}

Now let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = (r - r_0)} and we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(u) = V_0 + \frac{1}{2}Ku^2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dV(u)}{du} = Ku}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{vmatrix} 2k-m_1\omega^2 & -1\\ -k & 2k-m_2\omega^2 \end{vmatrix} =0 \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow -\omega^2u = -\frac{k}{m}u}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow - m \omega^2 -2k = k}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \omega = \sqrt{\frac{k}{m}}}

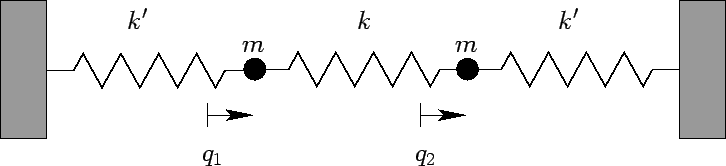
Two Atom Model

• Corresponds to putting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_2} in a potential well

• We can reduce this problem to particles on springs

• There is a spring with constant K holding the two atoms together. Also, we put them in a potential well such that we can imagine a spring connected each part individually to a wall, with spring constant Q

Here is an image of this problem. The problem used in class assumes k' = k.

• Solve via eigenvalue analysis

• Two Modes
  • Both Particles move in concert
  • Both Particles move opposite to each other

• If one of these particles are displaced (ignore the effects of the second) it will act as a linear Harmonic Oscillator, so that it will act as a simple sine wave.
  • However, if you take into account the second particle, the problem will not be so simple since there will be a superposition of two since waves creating a beat pattern. If the displacement is described by one of the modes above then there will be a simple sine wave.

We can write the equations of motion for these two particles as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\ddot u_1 = -Qu_1 - Ku_1 + Ku_2\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\ddot u_2 = -Ku_2 + Ku_1 - Qu_2\!}

,where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} are the spring constants, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} is mass, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} is displacement from the particles equilibrium position. This can be re-written as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\ddot u_1 = u_1(Q + K) + u_2(-K)\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\ddot u_2 = u_1(-K) + u_2(Q + K)\!}

We can create a matrix representation for this system of equations by letting

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow u = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}}

and choosing the interaction matrix, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{M}} to be

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} Q + K & -K \\ -K & Q + K \\ \end{bmatrix} }

Now we can rewrite our system of equations as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\ddot{u} = \mathbb{M}\overrightarrow{u}}

One dimensional mono-atomic chain

For this example, we imagine a chain of identical atoms, with mass Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} connected by springs, with spring constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} . Since this is only in one dimension we assume the particles only move in a direction parallel to the chain.

There are two forces that contribute to the displacement of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle nth} atom, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_n}

1)The force from the spring on the left Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K(u_n - u_{n-1})}

2)The force from the spring on the right Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K(u_{n+1} - u_n)}

Combining these we can write the total force as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\ddot{u}_n = -K[2u_n - u_{n-1} - u_{n+1}]\!}

...

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -m\omega^2 = -K[2u_n - u_{n-1} - u_{n+1}]\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -m\omega^2 = -K[2 - e^{iKa} - e^{-iKa}]\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(K) = 2\sqrt{\frac{K}{m}}|sin(Ka)|\!}

Sound waves - acoustic modes

When solving the eigenvalue problem for the coupled oscillator in one dimension, two independent modes become apparent. The acoustic sound mode corresponds to atoms moving together. The frequency of motion approaches zero as the wave vector approaches zero. The speed of the sound wave can be calculated using the approximate expression for frequency,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_\alpha \left (k \right )\approx c_\alpha\;k}

Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_\alpha} is the speed of sound and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha=1,2,3} is the dimension through which it propagates.

One dimensional diatomic chain: optical modes

Of the two modes, the optical mode has a higher frequency and unlike the acoustic mode, never approaches 0. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega \rightarrow } finite value, ${\vec {q}}\rightarrow 0$