PHZ3400 Symmetry Breaking

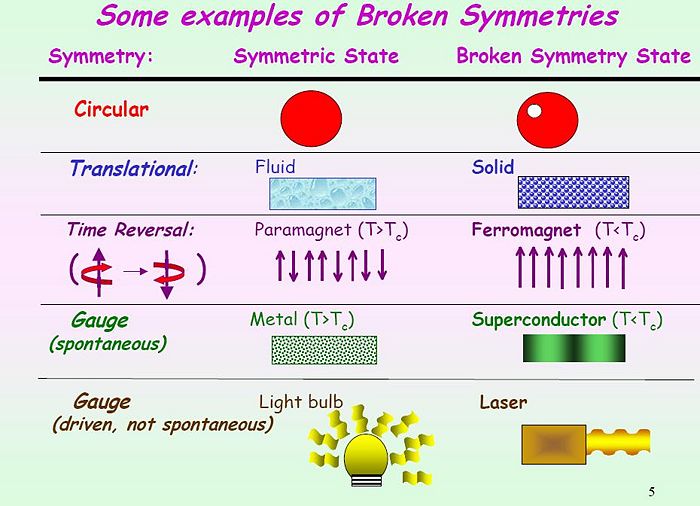
Classification of Phases: Symmetry

magnetization

A general definition of symmetry can be described as a precise and well defined concept of balance between two objects or functions. Symmetry can be found in many things in physics from the standard model, spacetime and supersymmetry. To our study in condensed matter, symmetry can be seen in crystals, magnets, superconductors, superfluids and their behaviors among multiple outside forces.

Symmetry Breaking in phase transitions can be viewed as the potential of some system to follow a certain path after crossing some critical point. This symmetry breaking arises from the fact that when the system crosses this critical point, it will follow one of two bifurcated paths of greater order. The path before the critical point is seen as of greater disorder and thus can be viewed as symmetrical since fluctuations on it don't change its overall appearance. Thus the symmetry of the initial state is broken when crossing the critical point. Symmetry breaking can consist of either first-order or second-order (continuous) phase transitions.

In recent years, a greater understanding of phase transitions has come from the study of thermodynamics. The third law of thermodynamics states that the entropy of a system tends to zero as the temperature tends to zero. Phenomena such as ferromagnetism, anti-ferromagnetism, superconductivity, superfluidity, and heavy fermion behaviour are examples of small interactions between particles which result in transitions to new ordered states at low temperatures. However, at low temperatures, it is possible to have some disorder in, for example, non-crystalline glassy systems. So it is perhaps more accurate to state that entropy tends to a limiting, constant value as the temperature tends to zero.

Weak interactions at low temperatures between particles in a system produce some type of order. These ordering processes are associated with symmetry breaking. Magnetic materials undergo a change at their Curie temperature from disorder and high symmetry in the paramagnetic phase to order and lower symmetry in the ferromagnetic phase. This symmetry change is due to the orientation of the magnetic dipoles of the material. When there is no magnetic field present, the dipoles are not directed in any particular order or direction in the paramagnetic phase. However, the dipoles are aligned in the ferromagnetic phase.

Spontaneous Symmetry Breaking and Thermodynamic Limit

Spontaneous Symmetry Breaking or SSB is referring to when an outside force interacts with the system, it will induce the falling out of symmetry. This breaking of symmetry can be seen in ferromagnetic materials. If the temperature is increased past the Curie point, any symmetry found in the material will vanish as well as the magnetic field. When the temperature is reduced from above the Curie point, the material has no net magnetization. When crossing over the Curie point, the magnetization will spontaneously choose a direction in which it will follow. Domains will form in random and will return to a magnetic state.

{{#ev:youtube| I6yQ61PARGw}}

When referring to the thermodynamic limit, we must visit the notion of Boltzmann's ergodic hypothesis. This hypothesis states that when a system is in equilibrium, all the states with the same energy will have exactly the same probability, thus all states will be occupied in a period of time. This is true for a small number of states, but is found to be broken when the number of spins in a material is infinite. This is considered the thermodynamic limit of the material. If, for example, we had a large system entirely composed of up-spins, and we wanted to visit the state in which all the spins were down, we must push a "domain wall" through the system. In a system of size $L$, the probability of visiting this state is

$P\sim e^{\frac {-\sigma L^{2}}{T}}$

The time to reach this state is proportional to the probability of visiting it. We can easily see that as the system size increases, the time will become incredibly large. Therefore, the ergodic hypothesis cannot be applied realistically to real-life situations, wherein we do not have an infinite amount of time to visit all states.

Ferromagnet and Curie-Weiss Theory

Vlad: we need all derivations presented in class, also reported here

The ferromagnet is, possibly a permanent magnet, any material which can exhibit magnetic properties or be induced by an external magnetic field. These properties depend on all the atoms within the material that align in some general direction according to the structure of the material. The alignments are determined by the dipole moment found in the atom due to the electrons spin and angular momentum.

Each dipole being induced by the neighboring dipoles will by classical theory cause the dipoles to alternate direction. However this force is greatly outweighed by the effect of the Pauli principle and the dipoles will align in the same direction. This property should keep the magnetic field in one direction, but is not seen among most ferromagnetic materials. Once a large system is considered with thousands of ions, classical forces will now outweigh quantum properties of the Pauli principle.

This will create what are called magnetic domains in which large sections of ions are aligned in one direction and then there is an opposing section of oppositely aligned ions. Between these two sections is what is called the domain wall where the dipoles will be opposing on each side of the wall. This gives the effect of a neutral material with no magnetic field since they cancel each other out.

So why when a magnetic field is induced into a material and then removed, does it not fall back to its original state? This situation causes all or most of the dipoles to flip and become locked into the same direction. Among the lattice of the material, when each ion flips it forces its way past defects in the lattice, causing it to become locked into position when the field is removed.

$M\simeq {\frac {T}{T_{c}}}({\frac {T-T_{c}}{T_{c}}})^{2}$

Curie's Law described at some temperature greater than the critical point in an external field H.

$M={\frac {H}{T-T_{c}}}[[Image:Example.jpg]]$

H is a similar field to the displacement field for electricity, but for magnetism. Here one can find the actual magnetic field B by:

$B=\mu _{o}H\!$

Magnetic susceptibility of the material is described by the partial derivative of magnetization to external field.

$\chi ={\frac {\partial {M}}{\partial {h}}}={\frac {1}{T-T_{c}}}$

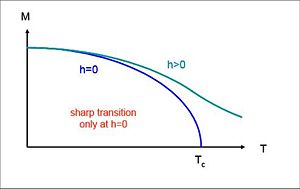
The relationship between magnetic susceptibility versus temperature is linked through the Curie temperature of the material. Combining equations of Curie's Law and magnetic susceptibility, the Curie-Weiss law is formed.

$\chi ={\frac {C}{T-T_{c}}}$

The denominator can become undefined, which is alarming. In nature, this represents spontaneous magnetization when T = T_c or below.

Caution must be taken near the critical point, in this case Curie Point. The mean field approximation does not accurately represent critical behavior near the critical point.

Ising Model

The Ising model is a mathematical model in physics used to show phase changes in a substance. The variables in the substance can either have a spin of +1 or -1. For the purpose of the model they are placed in a lattice structure. This arrangement could be a square lattice, hexagonal lattice, etc. Once the simulation begins the spins have the potential of interacting with their neighbors constructively or destructively depending on whether their spins are in the same or opposite directions. The overall outcome depends entirely on the majority known as the majority rule. This model depicts ferromagnetism at a microscopic level and shows us how a substance such as iron can become permanently magnetized.

Particle spins can be represented as follows:

$m=<S_{i}>$

$S_{i}=\pm 1\,$

Ferromagnetic Systems:

$H[S]=-\sum _{ij}J_{ij}S_{i}S_{j}\,$

$H[S]=Z/2\sum _{i=1}^{N}S_{i}\sum _{<j>}S_{j}\,$

In the presence of an external magnetic field h,

$H[S]=-\sum _{ij}JS_{i}S_{j}-h\sum _{i}S_{i}\,$

This can be approximate by replacing $S_{j}$ with its mean value and we end up with

$H[S]=-S_{i}(Jzm+h)\,$

We can use the boltzman distribution to write

$m={\frac {e^{\beta (h+Jzm)}-e^{-\beta (h+Jzm)}}{e^{\beta (h+Jzm)}+e^{-\beta (h+Jzm)}}}\,$

$m=tanh(\beta (h+Jzm))\,$

Other Examples of Symmetry Breaking

Other Examples of Symmetry Breaking Include:

Explicit symmetry breaking happens when the actual laws of the system are not invariant for the symmetry in question.

Dynamical symmetry breaking is a special form of spontaneous symmetry breaking. (Fermion condensates)

Chiral Symmetry Breaking

An anti-example of symmetry breaking would include infinite-order phase transitions. They are considered continuous but do not break symmetry.

Gauge Symmetry and Superconductivity

The transition of a metal from a normal state to a superconductive state is described by gauge symmetry breaking. A simple example of gauge symmetry is in the theory of gravity because the predictions of this theory are the same from any point of reference. In a conventional superconductor, gauge symmetry breaking occurs when electrons traveling in an unrelated way (normal metallic state) transitions to a state where the phases of the electron waves are highly correlated (superconducting state). We call these kinds of superconductors conventional because the effects of a moving particle in this material is invariant under direction.

YBCO zero-bias conductance peak due to d-wave broken reflection symmetry.

gauge symmetry

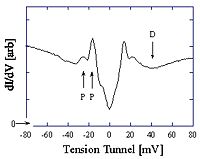
In an unconventional or high temperature superconductor, the effects on a particle moving in the material is dependent on the direction in which it moves. An example of a high Tc superconductor is YBCO,yttrium barium copper oxide(YBa₂Cu₃O₇). This material is extremely interesting because there is experimental evidence that in the superconducting state, YBCO breaks gauge and time-reversal symmetry. The superfluid He-3 was the only know material to do this and the discovery won the Nobel prize in 1966. YBCO shows a split in its zero-bias, low temperature conductance peak with no applied magnetic field. This happens because there exists two symmetries, d-wave and s-wave. The difference in the phases in these symmetries creates a spontaneous current and the current creates a magnetic filed which splits the conductance peak. The spontaneous current is what breaks the time-reversal symmetry because if a current is traveling in one direction, one can tell if it is moving forwards or backwards in time.

---

Sources

• Laura H. Greene, High Temperature Superconductors: Playground for Broken Symmetries, http://frontiers.physics.rutgers.edu/qcrit3_files/greene.pdf.
• Science Blog, New State Of Matter Found In High-Temperature Superconductors, http://www.scienceblog.com/community/older/1997/B/199701588.html