Phy5670/HubbardModel
The Hubbard Model
Introduction
The Hubbard Model is the simplest model used to describe interacting particles on a lattice. Proposed in 1963 by John Hubbard, it consists of a seemingly small correction to the tight-binding model of electrons on a lattice [1]. In Hubbard's model, a term is included to account for the interaction energy between particles on the same lattice site. The Hamiltonian is written thusly:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{H} = -2 t \sum_{\langle \vec{r},\vec{r'} \rangle}{(\hat{c}^\dagger_{\vec{r},\sigma}\hat{c}_{\vec{r'},\sigma} + \hat{c}^\dagger_{\vec{r'}\sigma}\hat{c}_{\vec{r}\sigma})} + U\sum_\vec{r}{\hat{n}_{\vec{r},\sigma'}\hat{n}_{\vec{r},\sigma}} }
The operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{c}^\dagger_{\vec{r},\sigma} } creates a particle in a Wannier state of spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma } at lattice position Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}} . Note that the sum over possible spins is implied. The summation in the kinetic energy (tight-binding) term is carried out over all nearest-neighbor bonds, or over all pairs Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\vec{r},\vec{r} + \vec{\delta}) } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\delta} } runs over half of the nearest-neighbor vectors. (For the square lattice, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\delta} \in \{ +a\hat{x},+a\hat{y} \} } . If the other two nn's were included, the sum as written would overcount the bonds.) The hopping integral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t } is the familiar term from the tight-binding model, and may in general depend on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\delta} } .
There exist multiple variations of this Hamiltonian, such as the Extended Hubbard Model, which takes into account the Coulomb interaction between particles on distant sites, with a term like
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{H}_{ex} = \sum_{\vec{r} \neq \vec{r'}}{\hat{n}_{\vec{r},\sigma}\hat{n}_{\vec{r'},\sigma'}} U(\vec{r}-\vec{r'}) }
As the length scales involved are can be on the order of a few angstroms, this interaction is not entirely trivial [8], and must be included to carefully look for charge density fluctuations. The undecorated model has proven complicated enough to resist complete solution, however, and will remain the main focus of this article.
For the last 40 years or so, this model has been studied intensively in hopes of gaining insight into the problem of interacting electrons, which is needed to better understand many strange properties of solids, such as superconductivity. The Hubbard Model also successfully fulfilled the prediction of Sir Neville Mott that the strange behavior of the class of materials known as Mott Insulators was due to electron-electron interactions [7,8]. These materials were expected to be conductors according to conventional band theory (which does not account for interactions), but were found instead to be insulating.
In cold atom systems, it has become possible to exactly create a Hubbard-like system, by optically trapping fermions at 'lattice' sites. With some further improvement of the characterization technologies for these cold systems (a non-trivial challenge, due to the delicacy of the experiments), it will be possible to experimentally determine the low-temperature phase diagram of the Hubbard model for the lowest three dimensions at any desired filling and magnetic field. [4]
Symmetry in the Hubbard Model
It is clear from the above form of the Hamiltonian that the total particle number of the system is conserved, since each particle destruction operator is conjuncted with another creation operator. Thus, the total charge is conserved.
It is equivalent to say that the system exhibits Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(1)} symmetry, in that the Hamiltonian is invariant under the transformation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{c}^\dagger_{\vec{r},\sigma} \rightarrow e^{-i \theta}\hat{c}^\dagger_{\vec{r},\sigma}} .
It is also possible to write this Hamiltonian in such a way that the spin symmetry of the system becomes apparent. The Hamiltonian can be written in terms of the spin operators, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\hat{S}} = \frac{\hbar}{2}\hat{c}^\dagger_{\vec{r},\alpha}\sigma_{\alpha,\beta}\hat{c}_{\vec{r},\beta}}
The on-site repulsion term, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U\sum_{\vec{r}}{\hat{c}^\dagger_{\vec{r},\uparrow}\hat{c}_{\vec{r},\uparrow}\hat{c}^\dagger_{\vec{r},\downarrow}\hat{c}_{\vec{r},\downarrow}}} must clearly involve some term like Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{S}^2} .
So, it is necessary to write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{S}^2} in terms of the raising and lowering operators.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{S}^2 = \frac{\hbar^2}{4} \sum_{a = 1}^3{\sigma^a_{\alpha \beta}\sigma^a_{\gamma \delta} \hat{c}^\dagger_{\alpha}\hat{c}_\beta \hat{c}^\dagger_\gamma\hat{c}_\delta} }
The two Pauli Matrices become:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{a = 1}^3{\sigma^a_{\alpha \beta}\sigma^a_{\gamma \delta} = 2\delta_{\alpha \delta}\delta_{\beta \gamma} - \delta_{\alpha \beta}\delta_{\gamma \delta}}}
So that, using the commutation relations between the creation and destruction operators,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{S}^2 = \frac{3 \hbar^2}{4}(\hat{c}^{\dagger}_{\uparrow} \hat{c}_{\uparrow} + \hat{c}^{\dagger}_{\downarrow} \hat{c}_{\downarrow}) - \frac{3 \hbar^2}{2}\hat{c}^\dagger_{\uparrow} \hat{c}_{\uparrow} \hat{c}^\dagger_{\downarrow} \hat{c}_{\downarrow} }
Now, the interaction term in the Hamiltonian can be written:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\mathbb{H}_{int}} = \frac{-2 \hbar^2 U}{3} \sum_{\vec{r}}{\vec{S}_{\vec{r}}\cdot\vec{S}_{\vec{r}}} + \frac{\hbar^2 U}{2} \sum_{\vec{r},\alpha} {\hat{c}^\dagger_{\vec{r},\alpha}\hat{c}_{\vec{r},\alpha}}}
Which, along with the tight-binding kinetic energy term, clearly conserves spin.
From the discussions in class, we can expect collective excitations of the ground state of this Hamiltonian in the form of fluctuations in both charge and spin density, which are exactly the excitations found in the one-dimensional solution. (These are referred to as holons and spinons, respectively.)
In addition, there is a symmetry between particles and holes in this model, which shows that the phase diagram must be symmetric for doping in either "direction" [1]. This can easily be seen by replacing the regular particle creation/destruction operators with "hole" destruction and creation operators:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{c}^\dagger_{\vec{r},\sigma} \rightarrow \hat{d}_{\vec{r},\sigma' \neq \sigma} ; \hat{c}_{\vec{r},\sigma} \rightarrow \hat{d}^\dagger_{\vec{r},\sigma' \neq \sigma}}
The sign changes in the interaction term that occur from going to normal ordering (of the hole operators, after the above substitution is made) cancel out, and the sign change in the kinetic energy is accompanied by a sign change of the hopping integral (since now a "hole" hopping is equivalent to a particle moving in the opposite direction). This symmetry is useful when considering the space of possible solutions to the Bethe Ansatz equations below.
The One-Dimensional Hubbard Model
It is a frustrating feature of this problem that it seems insoluble (though it only seems so, this has not been proven) in more than one dimension. In a single dimension, however, it is possible to find exactly the ground state energy and wavefunction. The simplest excitations of the one-dimensional system can also be described, which in turn leads to an approximate description of the thermodynamics of the model.
The solution was obtained in 1968 by Eliot Lieb and Fa-Yueh Wu, using the method of Bethe Ansatz.
To begin, the problem most simply consists of solving the Schrodinger equation:
Solution by Bethe Ansatz
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\mathbb{H}} |M,M'\rangle = E |M,M'\rangle }
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (M,M') } gives the number of spin down and spin up particles, respectively. Thanks to the particle-hole symmetry of the Hamiltonian, we need only consider states in which the total number of particles, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } is less than or equal to the number of lattice sites, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_l } . Additionally, thanks to the spin-symmetry, it is only necessary to consider solutions for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M \leq M' } .
Now, writing the state as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |M,M' \rangle = \sum_{1\leq x_j \leq N_a}{f(x_1...x_N)|x_1...x_N\rangle} }
The above state is written so that the spin down electrons are at sites Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{x_1...x_M\}} and the spin up electrons are at sites Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{x_{M+1}...x_N\}} .
Applying this to the Schrodinger equation gives the following:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2t\sum_{i=1}^N{f(x_1...x_{i+1}...x_N) + f(x_1...x_{i-1}...x_N)}+ U\sum_{i <j}{\delta(x_i - x_j)}f(x_1...x_N) = E f(x_1...x_N) }
Now, the Bethe Ansatz consists of properly choosing the form of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_1...x_N)} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_1...x_N) = \sum_P{[Q,P] e^{i \sum_{j=1}^N{k_{Pj}x_{Qj}}}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} are two permutations of sets of the numbers Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1...N)} , and the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{k_j\}} is a set of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} unequal numbers. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [Q,P]} represents a set of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N!\times N!} coefficients to be determined. Determination of these coefficients and the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{k_j\}} will give the final wavefunction.
The exact method of this solution is quite technical, and does not yield itself immediately to physical insight. The rest of the details are readily available in the 2002 paper by Lieb and Wu cited below.[1] The exact form of these wavefunctions is also presented by Woynarovich [2].
The results obtained are still of interest, without examining all of the gory details.
The predicted ground state at half-filing (one particle per site) is simply that of a one-dimensional antiferromagnet. Doping with either holes or particles allows for simple excitations in the form of spin waves (spinons, either up or down) and holons or anti-holons. These excitations each carry their namesake quantity only; spinons carry only spin, and holons carry only charge. This is referred to as "Spin-Charge Separation". Evidence for this phenomenon has been found experimentally in quasi one-dimensional materials.
Thermodynamic Properties
By virtue of the exact solution discussed above, it has been possible to calculate thermodynamic quantities for the one-dimensional Hubbard system. After finding the Gibbs Free Energy, the spin and charge susceptibilities have been found for all particle numbers, temperatures, and magnetic fields.
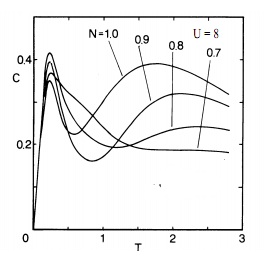
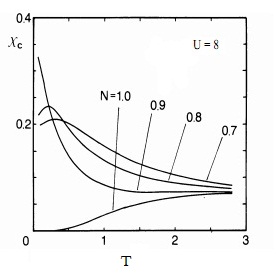
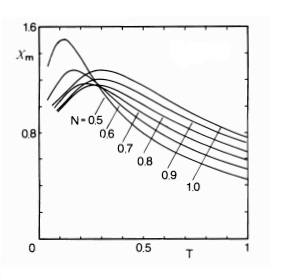
The following plots are reproduced from [2], showing these thermodynamic properties of the model for different filling levels.
Here, the specific heat is plotted with versus temperature. This is the contribution from the simple excitations, which were treated as a sort of string in the aforementioned paper.
The Charge Susceptibility shows the holon contribution to the electric response of the system.
Here, the Magnetic Susceptibility shows a small, but finite contribution due to the existence of spin waves (spinons).
Higher Dimensions
In higher dimensions, exact solution of the Hubbard Hamiltonian becomes impossible, at least for the dimensions of physical interest. Oddly enough, when the case of infinite dimensionality is considered, the model is numerically soluble! [5] It is quite interesting that the results in this seemingly unphysical limit actually correspond to a large degree with those found in lower dimensions. The model still exhibits many of the same features in the hase diagram; having paramagnetic and antiferromagnetic regions for varying ratios of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U/t} , and exhibiting the famous Mott Transition at a finite ratio.
For dimensions larger than one, the Mott transition between conductor and insulator actually occurs for finite Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U > 0} . In the single dimension, this occurs for any Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U > 0} , in the sense that only for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U = 0} does one find a conducting ground state (this, however, is only the right-binding model). A simple way to understand this is that in one dimension, electrons would have to pass through each other in order to move around as needed for conduction. If any sort of interaction is turned on, this becomes impossible, and an insulator is formed. In Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D \geq 2} , electrons may pass around each other, and conduction becomes possible for a finite repulsive interaction.
Broken symmetry is useful in considering the excited states of the system. In the ground state of an antiferromagnet, the system is not spin-symmetric, but the Hamiltonian remains so. Thus, as discussed earlier, in the presence of a broken-symmetry ground state in which the broken symmetry variable is conserved by the Hamiltonian, we expect to find hydrodynamic excitations in the density of that variable. There is also a generalized spin-rigidity of the system, exhibited in the spin-susceptibility shown above.
For all results in higher dimensions, numerical methods must be used, rather than analytic methods. Most of these successful methods belong to the class of techniques known as "Quantum Monte Carlo", which essentially consist of using the random-sampling Monte Carlo technique to evaluate integrals that arise in standard analytic approaches.
References
[1] "The One-Dimensional Hubbard Model: A Reminiscence" E. Lieb and F.Y Wu. arXiv:cond-mat/0207529v2 [1]
[2] "Thermodynamics and Excitations of the One-Dimensional Hubbard Model" arXiv:cond-mat/9904398v1 [2]
[3] J. Woynarovich 1982 J. Phys. C: Solid State Phys. 15 85. [3]
[4] "Magnetic Structure of an Imbalanced Fermi Gas in an Optical Lattice" arXiv:0909.0976v2 [cond-mat.quant-gas] [4]
[5] "The Hubbard Model at Infinite Dimensions: Thermodynamic and Transport Properties" arXiv:cond-mat/9208006v1 [5]
[6] J. Hubbard, Citation Classic No 22, June 2, 1980 [6]
[7] Mott, N. "Discussion of the Paper by de Boer and Verway" 1937 Proc. Phys. Soc. 49 72 [7]
[8] J. Hubbard, "Electron Correlations in Narrow Energy Bands" Proc. of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 276, No. 1365 (Nov. 26, 1963), pp. 238-257 [8]