Phy5670/Phonon in Graphene

Introduction

Recently, graphene rapidly become a hot topic. Following that, lots of vagarious properties come out because of its honeycomb structure. Here, we will discuss about phonon dispersion in graphene. We first explore a method to calculate phonon dispersion relations within a force constant model, where inter-particle forces are represented by spring constants. Then we use this general approach to discuss the phonon dispersion relations for 2D graphene sheet.

Structure of Graphene

Fig.1: Honeycomb lattice of graphene.

Carbon atoms in graphene are constructed on a honeycomb lattice, which is shown in Fig. 1. The circle and solid point together combine into a two-point basis in the Bravais lattice. The carbon-carbon distance is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\simeq 1.42{\AA}} . The primitive vectors are

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{a}_1=\frac{\sqrt{3}}{2}a\hat{x}+\frac{3}{2}a\hat{y}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{a}_2=-\frac{\sqrt{3}}{2}a\hat{x}+\frac{3}{2}a\hat{y}}

Then the reciprocal lattice parameters can by generated by using Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{b_i}\cdot \vec{a_j}=2\pi\delta_{ij}, (i,j=1,2)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{b}_1=\frac{2\pi}{a}(\frac{\sqrt{3}}{3}\hat{x}+\frac{1}{3}\hat{y})}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{b}_2=\frac{2\pi}{a}(-\frac{\sqrt{3}}{2}a\hat{x}+\frac{3}{2}a\hat{y})}

General phonon dispersion relations

Before we move on to solving phonon in graphene, we discuss how to solve phonon problem for general case. Suppose we have particle system, which is constructed by unit cells. For each unit cell, there are N atoms. Let's use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}_i=(x_i, y_i, z_i)} to represent the displacement of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}} particle coordinate. Thus, the equations of motion for these N atoms in each unit are:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_i\ddot\vec{u}_i=\sum_{j}K^{(ij)}(\vec{u}_j-\vec{u}_i)} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad (i=1,2,...N)}

where,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_i} is the mass of each particle, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K^{(ij)}} is the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3*3} force constant tensor between the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}} and the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^{th}} particles.

By Fourier transform, we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}_i=\frac{1}{\sqrt{N_\Omega}}\sum_{\vec{k^'}}e^{-i(\vec{k^'}\cdot\vec{R}_i-\omega t)}\vec{u}_\vec{k^'}^{(i)}}

and, in turn,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}_\vec{k}^{(i)}=\frac{1}{\sqrt{N_\Omega}}\sum_{\vec{R}_i}e^{i(\vec{k}\cdot\vec{R_i}-\omega t)}\vec{u_i}}

where, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_\Omega} is the number of the wave vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{k_i}} in the first Brillouin zone, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{R_i}} is the original position of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}} particle.

We assume that all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u_i}} have the same eigenfreguency Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} , which means:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ddot{\vec{u}_i}=-\omega^2\vec{u}_i}

So,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\sum_{j} K^{(ij)}-M_i\omega^2)\sum_{\vec{k^'}}e^{-i\vec{k^'}\cdot\vec{R}_i}\vec{u}_{\vec{k^'}}^{(i)}=\sum_{j}K^{(ij)}\sum_{\vec{k^'}}e^{-i\vec{k^'}\cdot\vec{R}_j}\vec{u}_\vec{k^'}^{(j)}}

Multiplying Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i\vec{k}\cdot\vec{R}_i}} and taking the summation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{R}_i} , we obtain:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\vec{R_i}}\exp{i(\vec{k}-\vec{k^'})\cdot\vec{R_i}}=N_\Omega\delta_{\vec{k},\vec{k^'}}}

Thus,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\sum_{j} K^{(ij)}-M_i\omega^2(\vec{k})I)\vec{u}_\vec{k}^{(i)}-\sum_{j}K^{(ij)}e^{i\vec{k}\cdot\Delta\vec{R}_{ij}}\vec{u}_\vec{k}^{(j)}=0}

where, I is a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3\times 3} unit matrix, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\vec{R_{ij}}=\vec{R_i}-\vec{R_j}} is the relative coordinate of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}} particle and the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^{th}} particle.

By using boundary conditions, all j can be shifted to a site in the original unit cell. And, when j and j' sites are equivalent to each other (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{R}_j} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{R}_{j^'}} ) differ by a lattice vector), we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}_\vec{k}^{(j)}=\vec{u}_\vec{k}^{(j^')}} . Thus, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}_\vec{k}^{(j)}} is contained within the original unit cell.

For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K^{(ij')}} , there will be a phase factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i\vec{k}\cdot\Delta\vec{R}_{ij'}}}

Thus, for a given Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{k}} , eigenfuctions can be written as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D(\vec{k})\vec{u}_\vec{k}=0}

in which, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D(\vec{k})} is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3N\times3N} dynamical matrix, and is constructed by small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3\times 3} matrices Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^{(ij)}(\vec{k}) \quad (i,j=1,2,...,N)} .

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^{(ij)}(\vec{k})=(\sum_{j''} K^{(ij'')}-M_i\omega^2(\vec{k})I)\delta_{ij}-\sum_{j'}K^{(ij)}e^{i\vec{k}\cdot\Delta\vec{R}_{ij'}}}

Phonon dispersion relations for graphene

Fig.2: Neighbor atoms of a graphitic plane up to 4th nearest neighbors for (a) an A atom and (b) a B atom at the center denoted by solid circles. From the lst to the 4th neighbor atoms, we plot open circles (lst neighbor), solid squares (2nd), open squares (3rd), and open hexagons (4"), respectively. Circles connecting the same neighbor atoms are for guides to the eye.

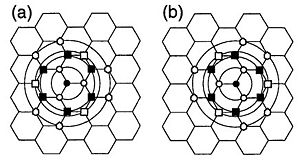
Now, under the master of calculation method for phonon dispersion in general case, we now can study phonon dispersion relations for graphene. For graphene sheet, there are two carbon particles, A and B, in the unit cell, we have six coordinate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}_\vec{k}} . So, dynamical matrix D is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6\times 6} , which can be written into Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3\times 3} matrices. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^{AA}, D^{AB}, D^{BA}, D^{BB}} .

$D={\begin{pmatrix}D^{AA}&D^{AB}\\D^{BA}&D^{BB}\end{pmatrix}}$

For particle A in the Fig.2, three nearest-neighbor particles are $B_{1},B_{2},B_{3}$(on the circle I). The contribution of them contain in $D^{AB}$. In the circle II, all A particles are the next-nearest-neighbor, which contribute to $D^{AA}$. Then we can get $D^{BA}$ and $D^{BB}$.

For the force constant tensor $K^{(ij)}$. First, we consider $A$ and $B_{1}$.

$K^{(A,B_{1})}={\begin{pmatrix}\phi _{r}^{(1)}&0&0\\0&\phi _{ti}^{(1)}&0\\0&0&\phi _{to}^{(1)}\end{pmatrix}}$

in which, $\phi _{r}^{(n)},\phi _{ti}^{(n)}$ and $\phi _{to}^{(n)}$ are the force constant parameters in the radial, in-plane, and out-of-plane tangential directions of the $n^{th}$ nearest neighbors.

The corresponding phase factor is $e^{i{\vec {k}}\cdot \Delta {\vec {R}}_{ij}}=e^{-ik_{x}a/{\sqrt {3}}}$

For the two other nearest-neighbor particles $B_{2}$, $B_{3}$, we can get $K^{(A,B_{m})},m=2,3$ by rotating the matrix.

$K^{(A,B_{m})}=U_{m}^{-1}K^{(A,B_{1})}U_{m}$

where, $U_{m}={\begin{pmatrix}cos\theta _{m}&sin\theta _{m}&0\\-sin\theta _{m}&cos\theta _{m}&0\\0&0&1\end{pmatrix}}$

Thus, we can get force constant tensor for $B_{2}$ $(-{\frac {a}{2{\sqrt {3}}}},{\frac {a}{2}},0)$. Here $\theta _{2}={\frac {2\pi }{3}}$

$K^{(A,B_{2})}={\frac {1}{4}}{\begin{pmatrix}\phi _{r}^{(1)}+3\phi _{ti}^{(1)}&{\sqrt {3}}(\phi _{ti}^{(1)}-\phi _{r}^{(1)})&0\\{\sqrt {3}}(\phi _{ti}^{(1)}-\phi _{r}^{(1)})&3\phi _{r}^{(1)}+\phi _{ti}^{(1)}&0\\0&0&\phi _{to}^{(1)}\end{pmatrix}}$

The corresponding phase factor is $e^{-ik_{x}a/(2{\sqrt {3}})+ik_{y}a/2}$

And the force constant tensor for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_3} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-\frac{a}{2\sqrt{3}},-\frac{a}{2},0) } . Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_3=\frac{4\pi}{3}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K^{(A,B_3)}=\frac{1}{4} \begin{pmatrix} \phi_{r}^{(1)}+3\phi_{ti}^{(1)} & \sqrt{3}(-\phi_{ti}^{(1)}+\phi_{r}^{(1)} ) & 0\\ \sqrt{3}(-\phi_{ti}^{(1)}+\phi_{r}^{(1)}) & 3\phi_{r}^{(1)}+\phi_{ti}^{(1)} & 0 \\ 0&0&\phi_{to}^{(1)} \end{pmatrix}}

The corresponding phase factor is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-ik_xa/(2\sqrt{3})-ik_ya/2}}

So, using formula of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^{(ij)}} , we obtain:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^{AB}=-(K^{(A,B_1)}e^{-ik_xa/ \sqrt{3}}+K^{(A,B_2)}e^{-ik_xa/(2\sqrt{3})+ik_ya/2}+K^{(A,B_3)}e^{-ik_xa/(2\sqrt{3})-ik_ya/2})}

Now, let's move on to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^{BA}} .

The positions of A atoms are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1(0,0,0)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_2(\frac{\sqrt{3}}{2}a,\frac{1}{2}a,0)} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_2(\frac{\sqrt{3}}{2}a,-\frac{1}{2}a,0)} . The corresponding phase factors are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_1=\pi} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_2=\pi/3} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_2=5\pi/3} respectively.

By the same analysis above, we can get:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K^{(BA_1)}=-\begin{pmatrix} \phi_r^{(1)} & 0 & 0 \\ 0 & \phi_{ti}^{(1)} & 0 \\ 0 & 0 & \phi_{to}^{(1)} \end{pmatrix}} The corresponding phase factor is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i\vec{k}\cdot\Delta\vec{R}_{ij}} =e^{-ik_xa/ \sqrt{3}}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K^{(B,A_2)}=-\frac{1}{4} \begin{pmatrix} \phi_{r}^{(1)}+3\phi_{ti}^{(1)} & \sqrt{3}(-\phi_{ti}^{(1)}+\phi_{r}^{(1)} ) & 0\\ \sqrt{3}(-\phi_{ti}^{(1)}+\phi_{r}^{(1)}) & 3\phi_{r}^{(1)}+\phi_{ti}^{(1)} & 0 \\ 0&0&\phi_{to}^{(1)} \end{pmatrix}}

The corresponding phase factor is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-i\sqrt{3}k_xa/2+ik_ya/2}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K^{(B,A_3)}=-\frac{1}{4} \begin{pmatrix} \phi_{r}^{(1)}+3\phi_{ti}^{(1)} & \sqrt{3}(\phi_{ti}^{(1)}-\phi_{r}^{(1)} ) & 0\\ \sqrt{3}(\phi_{ti}^{(1)}-\phi_{r}^{(1)}) & 3\phi_{r}^{(1)}+\phi_{ti}^{(1)} & 0 \\ 0&0&\phi_{to}^{(1)} \end{pmatrix}}

The corresponding phase factor is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-i\sqrt{3}k_xa/2-ik_ya/2}}

Thus, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^{BA}=-(K^{(B,A_1)}e^{-ik_xa/ \sqrt{3}}+K^{(B,A_2)}e^{-i\sqrt{3}k_xa/2+ik_ya/2}+K^{(B,A_3)}e^{-i\sqrt{3}k_xa/2-ik_ya/2})}

Here, we just consider the first nearest neighbors, so Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^{AA}=-M\omega^2I} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^{BB}=-M\omega^2I} .

So, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=\begin{pmatrix} D^{AA} & D^{AB} \\ D^{BA} & D^{BB} \end{pmatrix}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\begin{pmatrix} -M\omega^2I & -(K^{(A,B_1)}e^{-ik_xa/ \sqrt{3}}+K^{(A,B_2)}e^{-ik_xa/(2\sqrt{3})+ik_ya/2}+K^{(A,B_3)}e^{-ik_xa/(2\sqrt{3})-ik_ya/2}) \\ -(K^{(B,A_1)}e^{-ik_xa/ \sqrt{3}}+K^{(B,A_2)}e^{-i\sqrt{3}k_xa/2+ik_ya/2}+K^{(B,A_3)}e^{-i\sqrt{3}k_xa/2-ik_ya/2}) & -M\omega^2I \end{pmatrix} }

Fig.3: The phonon dispersion curves by considering first nearest neighbors.

Fig.4: The phonon dispersion in reference.

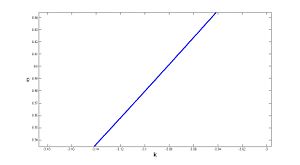
Now, we need the force constants Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_r^{(1)}} , $\phi _{ti}^{(1)}$ and $\phi _{to}^{(1)}$, we can get them by matching experimental results. Here are the values of the force constants from reference: $\phi _{r}^{(1)}=36.50\times 10^{4}dyn/cm$, $\phi _{ti}^{(1)}=24.50\times 10^{4}dyn/cm$ and $\phi _{to}^{(1)}=9.82\times 10^{4}dyn/cm$.

Substituting these values into $D$, then from $det(D)=0$ we can get the relationship between $\omega$ and $k$.

Then we can draw the phonon dispersion relation between $\omega$ and $k_{x}$ on the right hand side Fig. 3.

Let's comparing our results with the experiment-theory matching result in the reference in Fig. 4.

In our result, we have two in-plane acoustic branches which show a linear k dependence (here we just show $k_{x}$ branch, for $k_{y}$ branch, the result is similar). In the reference, Fig.4 shows the phonon dispersion branches of graphene. The three phonon dispersion branches, which originate from the $\Gamma$-point of the BRILLOUIN zone correspond to acoustic modes: an out-of plane mode (ZA), an in-plane transverse mode (TA), and in-plane longitudinal (LA), listed in order of increasing energy. The remaining three branches correspond to optical modes: one out-of plane mode (ZO), and two in-plane modes (TO) and (LO). Here, $k_{x}$ we showed in Fig. 3 is the branch of in-plane longitudinal (LA) branch in Fig. 4. If we consider more nearest neighbors to 4th order. The result will match better. And we also can calculate other branches by the same way.