Phy5670/RPA

The Single-Particle Shell Model

A finite interacting assembly, such as nucleons inside a nuclei, is extremely complicated. Fortunately, most properties of finite nuclei can be understood with approximate, solvable, single-particle potentials.

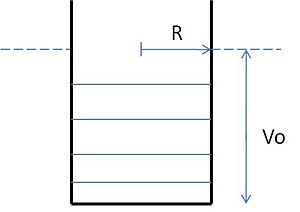
First, let us consider the simplest single-particle potential, an infinite square well (Fig. 1). The solutions to the Schrodinger equation that are finite at the origin are

Fig.1 Square-well potential

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{nlm} = N_{nl} j_{l}(kr) Y_{lm}(\theta, \phi) }

with energy

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = \frac{\hbar^2 k^2}{2m} - V_{o} }

The wave function must vanish at the boundary Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{l}(kR) = 0 } giving the eigenvalue spectrum

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{nl} R = X_{nl} }

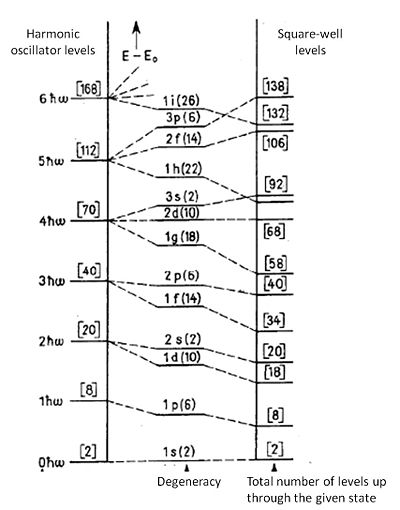
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{nl} } is the nth zero of the lth spherical Bessel function, excluding the origin and including the zero at the boundary. The ordering of these zeros is shown on the right side of Fig. 4. The normalization integral can be evaluated explicitly to give

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{nl}^2 = \frac{2}{R^3} \frac{1}{j_{l+1}^2 (X_{nl})} }

which yields one approximate set of single-particle wave functions.

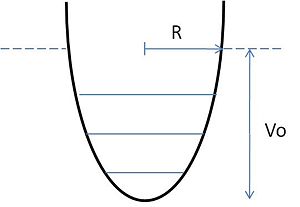
A second simple solvable potential is the harmonic oscillator (Fig. 2). We write the potential as

Fig.2 Harmonic potential

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r) = -V_{o} [1-(\frac{r}{R})^2] = -V_{o} + \frac{1}{2} m \omega^2 r^2 }

with

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{V_{o}}{R^2} = \frac{1}{2} m \omega^2 }

and look for solutions to the Schrodinger equation in the form

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{nlm} = \frac{u_{nl}(r)}{r} Y_{lm}(\theta, \phi) }

The radial function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{nl}(r) } then satisfies the equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [- \frac{\hbar^2}{2m} \frac{d^2}{dr^2} + \frac{1}{2} m \omega^2 r^2 + \frac{\hbar^2}{2m} \frac{l(l+1)}{r^2} - (\epsilon_{nl} + V_{o})] u_{nl}(r) = 0 }

whose solutions are Laguerre polynomials

Fig.3 Nuclear potential

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{nl}(q) = N_{nl} q^{l+1} e^{-q^2 /2} L_{n-1}^{l+1/2}(q^2) }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{p}^{a}(z) = \frac{\gamma(a+p+1)}{\gamma(p+1)} \frac{e^z}{z^a} \frac{d^p}{dz^p} (z^{a+p} e^{-z}) }

with

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = \frac{r}{b}; \hbar \omega = \frac{\hbar^2}{mb^2} }

Fig.4 Level system of the three dimensional isotropic harmonic oscillator (on left) and the infinite square well (on right). [2]

As in the square well, n denotes the number of nodes in the radial wave function including the one at infinity and takes the values

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = 1, 2, ..., \infty }

These functions can be normalized using standard formulas

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{nl}^2 = \frac{2(n-1)!}{b[\gamma(n+l+1/2)]^3} }

The resulting eigenvalue spectrum of the three-dimensional oscillator is well known

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{nl} = \hbar \omega (N + \frac{3}{2}) - V_o; N = 2(n-1)+l = 0, 1, 2, ..., \infty }

and is plotted on the left side of Fig. 4. These degenerate levels contain states of different l and are spaced a distance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega } apart. We shall refer to these as the oscillator shells.

The true nuclear single-particle well has a finite depth (Fig. 3). Nevertheless, the low-lying levels with large binding energies are essentially unchanged by extending the walls of the potential to infinity. For these states, at least, the real Hartree-Fock potential presumably has a shape intermediate between the square well and the oscillator, and we can easily interpolate between the two cases. Both n and l remain good quantum numbers as the bottom edge of the square well is rounded or the bottom of the oscillator is flattened out. The highest l states have the largest probability of being near the edge of the potential, and their energy will be lowered in going from the oscillator to the square well.

Collective Modes of Nuclei

Fig.5 Photoneutron cross section of O-16 up to 30MeV showing resonances due to levels in O-16. [4]

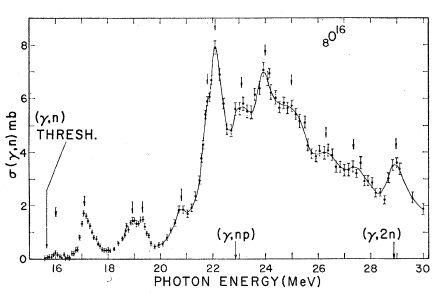
For spherically symmetric doubly magic nuclei like O-16, Ca-40, or Pb-208, their lowest excitations should lie at about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega } according to the harmonic oscillator approximation of the nuclear shell model. For O-16 the experimental shell difference between 1p and 2s-1d shells is roughly 11.5 MeV. However, in the spectrum of O-16 (Fig. 5) among other states there exist a state (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J^{\pi} = 3^{-} } , T = 0) at 6.14 MeV, and around 22 MeV a 5 MeV broad resonance which is called the giant dipole resonance of quantum numbers Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J^{\pi} = 1^{-}} , T = 1. It can be shown that mainly Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \hbar \omega } excitations are involved in this resonance. Therefore, the pure shell model also fails to explain the high energy of the giant dipole resonance.

It turns out that these excitations can only be explained if we suppose that coherent participation by many nucleons takes place in the nuclues, in other words, many nucleons are believed to take part in similar fashion to the shape vibrations of the nuclear drop. Such collective excitations generally fulfill the following criteria:

(i) Their electromagnetic transition probabilities have a collective strength such that they are one to two orders of magnitude larger than the single-particle transitions.

(ii) They show up in the spectra of different nuclei over the periodic table with great regularity. The giant dipole resonance, for example, has been observed throughout the periodic table and its excitation energy varies slowly with mass number.

There are many different types of modes a nucleus can assume according to its various degrees of freedom: A nucleus can be deformed, displaced, or compressed; the densities of the proton and neutron can vibrate in and out of phase; there can be vibrations in spin and isospin, and so on.

(a) In the first place, there are vibrations of the local density of the nucleus in space. Since the angular dependence of such vibrations is already determined by the angular momentum, we can only allow for different radial shapes. The simplest example are the surface vibrations of a sphere with a sharp surface. There are also excitations called breathing modes where the density in the interior is also changed.

(b) A quite different type of motion, which also involves only the spatial degrees of freedom, is given by the non-local part of the transition density matrix. An example is the nuclear twist mode, where the local density of the nucleus stays unchanged and only the intrinsic velocity distribution oscillates.

(c) The isospin is an additional degree of freedom. The protons can vibrate in phase or out of phase with the neutrons. In either case, we eventually have as oscillating charge distribution at a fixed point. This corresponds to polarization waves in the nucleus.

(d) Finally, we also have the spin degree of freedom. The corresponding vibrations produce spin waves.

Fig.6 Schematic picture of the shell structure in a closed shell nucleus and possible 1p-1h excitations.

In finite realistic nuclei these modes are not precisely realized. Instead, there are always more or less drastic admixtures of less collective states. A more useful way to classify the modes is based on the shell model in its simplest version - the harmonic oscillator.

Figure 6 shows schematically the shell structure for a closed shell nucleus (as Pb-208). We have alternating shells with positive and negative parities separated by an energy difference of roughly Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \hbar \omega } . For a closed shell nucleus, the Fermi surface lies just between two shells and we therefore find particle-hole (ph) pairs of a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \hbar \omega } excitation with negative parity, or a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \hbar \omega } excitation with positive parity, or a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3 \hbar \omega } excitation with negative parity, and so on. For nuclei between closed shells we also have, in addition, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \hbar \omega } excitations within the shell. For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J^{ \pi} = 3^{-} } , for instance, people find a very collective state consisting mainly of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \hbar \omega } excitations and a second one consisting mainly of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3 \hbar \omega } excitations [5,6].

Polarization Propagator

To study excited states in many-fermion systems, the limit of the two-particle (tp) propagator is used

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{ph} (\alpha, \beta^{-1}; \gamma, \delta^{-1}; t-t') = \lim_{t_{\beta} \rightarrow t^{+}} \lim_{t_{\gamma} \rightarrow t'^{+}} G_{II} (\alpha t, \bar{\delta} t', \bar{\beta} t_{\beta}, \gamma t_{\gamma}) = -\frac{i}{\hbar} \langle \psi_{o}^{N}| T [a_{\bar{\beta}}^{H+}(t) a_{\alpha}^{H}(t) a_{\gamma}^{H+} (t') a_{\bar{\delta}}^{H} (t')] | \psi_{o}^{N} \rangle } (Eq. 1)

where "ph" means "particle-hole pairs". Substituting the explicit form of the Heisenberg operators and inserting a complete set of N-particle state one has

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{ph} (\alpha, \beta^{-1}; \gamma, \delta^{-1}; t-t') = -\frac{i}{\hbar} \langle \psi_{o}^{N}| T [e^{iHt/\hbar}a_{\bar{\beta}}^{+}e^{-iHt/\hbar} e^{iHt/\hbar}a_{\alpha}e^{-iHt/\hbar} e^{iHt'/\hbar}a_{\gamma}^{+}e^{-iHt'/\hbar} e^{iHt'/\hbar}a_{\bar{\delta}}e^{-iHt'/\hbar}] | \psi_{o}^{N} \rangle }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -\frac{i}{\hbar} \langle \psi_{o}^{N}| T [e^{iHt/\hbar}a_{\bar{\beta}} a_{\alpha}e^{-iHt/\hbar} e^{iHt'/\hbar}a_{\gamma}^{+} a_{\bar{\delta}}e^{-iHt'/\hbar}] | \psi_{o}^{N} \rangle }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -\frac{i}{\hbar} \sum_{n}^{} \langle \psi_{o}^{N}| T [e^{iHt/\hbar}a_{\bar{\beta}} a_{\alpha}e^{-iHt/\hbar} | \psi_{n}^{N}\rangle \langle \psi_{n}^{N} | e^{iHt'/\hbar}a_{\gamma}^{+} a_{\bar{\delta}}e^{-iHt'/\hbar}] | \psi_{o}^{N} \rangle }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -\frac{i}{\hbar} \langle \psi_{o}^{N}| T [e^{iHt/\hbar}a_{\bar{\beta}} a_{\alpha}e^{-iHt/\hbar} | \psi_{o}^{N}\rangle \langle \psi_{o}^{N} | e^{iHt'/\hbar}a_{\gamma}^{+} a_{\bar{\delta}}e^{-iHt'/\hbar}] | \psi_{o}^{N} \rangle -\frac{i}{\hbar} \sum_{n \neq 0}^{} \langle \psi_{o}^{N}| T [e^{iHt/\hbar}a_{\bar{\beta}} a_{\alpha}e^{-iHt/\hbar} | \psi_{n}^{N}\rangle \langle \psi_{n}^{N} | e^{iHt'/\hbar}a_{\gamma}^{+} a_{\bar{\delta}}e^{-iHt'/\hbar}] | \psi_{o}^{N} \rangle}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -\frac{i}{\hbar} \langle \psi_{o}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{o}^{N} \rangle \langle \psi_{o}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{o}^{N} \rangle - \frac{i}{\hbar} [ \sum_{n \neq 0}^{} \theta (t-t') e^{i(E_{o}^{N} - E_{n}^{N})(t-t')/\hbar} \langle \psi_{o}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{o}^{N} \rangle + \sum_{n \neq 0}^{} \theta (t'-t) e^{i(E_{o}^{N} - E_{n}^{N})(t'-t)/\hbar} \langle \psi_{o}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{o}^{N} \rangle ] } (Eq. 2)

where the definition of the time-ordering operator in terms of step functions is used also. The so-called polarization propagator is defined by Eq. (2) which includes the excited states only:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi (\alpha, \beta^{-1}; \gamma, \delta^{-1}; t-t') = G_{ph} (\alpha, \beta^{-1}; \gamma, \delta^{-1}; t-t') + \frac{i}{\hbar} \langle \psi_{o}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{o}^{N} \rangle \langle \psi_{o}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{o}^{N} \rangle }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = - \frac{i}{\hbar} [ \sum_{n \neq 0}^{} \theta (t-t') e^{i(E_{o}^{N} - E_{n}^{N})(t-t')/\hbar} \langle \psi_{o}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{o}^{N} \rangle + \sum_{n \neq 0}^{} \theta (t'-t) e^{i(E_{o}^{N} - E_{n}^{N})(t'-t)/\hbar} \langle \psi_{o}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{o}^{N} \rangle ]} (Eq. 3)

By employing the integral formulation of the step function, that is,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta (t-t_{o}) = \frac{-1}{2 \pi i} \int \frac{dE'}{E'+i \eta} e^{-iE'(t-t_{o})/\hbar} }

one can transform the polarization propagator, Eq. (3), into its Lehmann representation as following: (Let us calculate the first term in Eq. (3) first and let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau = t-t' } .)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi (\alpha, \beta^{-1}; \gamma, \delta^{-1}; E) = \int \pi (\alpha, \beta^{-1}; \gamma, \delta^{-1}; \tau) e^{iE \tau /\hbar} d \tau }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = - \frac{i}{\hbar} \sum_{n \neq 0}^{} \int \theta (\tau) e^{i(E_{o}^{N} - E_{n}^{N})\tau/\hbar} e^{iE \tau /\hbar} d \tau \langle \psi_{o}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{o}^{N} \rangle }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2 \pi \hbar} \sum_{n \neq 0}^{} \int \int \frac{dE'}{E'+i \eta} e^{-iE' \tau /\hbar} e^{i(E_{o}^{N} - E_{n}^{N})\tau/\hbar} e^{iE \tau /\hbar} d \tau \langle \psi_{o}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{o}^{N} \rangle }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2 \pi \hbar} \sum_{n \neq 0}^{} \int \int \frac{dE'}{E'+i \eta} e^{-i(E'-E-(E_{o}^{N}-E_{n}^{N})) \tau/\hbar} d \tau \langle \psi_{o}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{o}^{N} \rangle }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2 \pi \hbar} \sum_{n \neq 0}^{} \int \frac{dE'}{E'+i \eta} 2 \pi \hbar \delta(E'-E-(E_{o}^{N}-E_{n}^{N})) d \tau \langle \psi_{o}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{o}^{N} \rangle }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \sum_{n \neq 0}^{} \frac{\langle \psi_{o}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{o}^{N} \rangle}{E+(E_{o}^{N}-E_{n}^{N})+i \eta} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \sum_{n \neq 0}^{} \frac{\langle \psi_{o}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{o}^{N} \rangle}{E-(E_{n}^{N}-E_{0}^{N})+i \eta} }

Similarly, the second term in Eq. (3) cab be Fourier transformed into this form:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \sum_{n \neq 0}^{} \frac{\langle \psi_{o}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{o}^{N} \rangle}{E+(E_{n}^{N}-E_{0}^{N})-i \eta} }

Hence we obtain the polarization propagator in Lehmann representation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi (\alpha, \beta^{-1}; \gamma, \delta^{-1}; E) = \sum_{n \neq 0}^{} \frac{\langle \psi_{o}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{o}^{N} \rangle}{E-(E_{n}^{N}-E_{0}^{N})+i \eta} - \sum_{n \neq 0}^{} \frac{\langle \psi_{o}^{N} | a_{\gamma}^{+} a_{\bar{\delta}} | \psi_{n}^{N} \rangle \langle \psi_{n}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{o}^{N} \rangle}{E+(E_{n}^{N}-E_{0}^{N})-i \eta} } (Eq. 4)

The polarization propagator incorporates the energy of excited states of N-particle system in its denominator, whereas its numerator contains the transition amplitudes connecting the ground state with those excited states.

Random Phase Approximation

First, let us consider the non-interacting limit of the polarization propagator, which can be obtained from Eq. (3) by replacing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H } by the non-interacting Hamiltonian $H_{o}$ and replacing $|\psi _{o}^{N}\rangle$ by the non-interacting ground state $|\phi _{o}^{N}\rangle$,

$\pi ^{(o)}(\alpha ,\beta ^{-1};\gamma ,\delta ^{-1};t-t')=G_{ph}^{(o)}(\alpha ,\beta ^{-1};\gamma ,\delta ^{-1};t-t')+{\frac {i}{\hbar }}\langle \phi _{o}^{N}|a_{\bar {\beta }}^{+}a_{\alpha }|\phi _{o}^{N}\rangle \langle \phi _{o}^{N}|a_{\gamma }^{+}a_{\bar {\delta }}|\phi _{o}^{N}\rangle$

$=-{\frac {i}{\hbar }}[\theta (t-t')\theta (\alpha -F)\theta (F-\beta )\delta _{\alpha ,\gamma }\delta _{\beta ,\delta }e^{-i(E_{\alpha }-E_{\beta })(t-t')/\hbar }+\theta (t'-t)\theta (F-\alpha )\theta (\beta -F)\delta _{\alpha ,\gamma }\delta _{\beta ,\delta }e^{-i(E_{\beta }-E_{\alpha })(t'-t)/\hbar }]$ (Eq. 5)

Fig.7

Fig.8

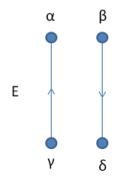
The first term corresponds to the independent propagation of a particle with $\alpha (\gamma )$ from $t'$ to $t$, and a hole with $\beta (\delta )$ from $t$ to $t'$. The second term exchanges the role of $t$ and $t'$, as well as that of the quantum numbers, and corresponds to the independent hole-particle (hp) propagation. See Fig. 7. Using the integral representation of the step functions in Eq. (5), the Fourier transform of $\pi ^{o}$ is obtained as

$\pi ^{(o)}(\alpha ,\beta ^{-1};\gamma ,\delta ^{-1};E)=\delta _{\alpha ,\gamma }\delta _{\beta ,\delta }[{\frac {\theta (\alpha -F)\theta (F-\beta )}{E-(E_{\alpha }-E_{\beta })+i\eta }}-{\frac {\theta (F-\alpha )\theta (\beta -F)}{E+(E_{\beta }-E_{\alpha })-i\eta }}]$ (Eq. 6)

The poles of the non-interacting polarization propagator correspond to ph states obtained by removing a particle from an occupied level and placing it in an empty level of $H_{o}$, as shown in Fig. 8. The numerator shows that the ph pair added to the non-interaction ground state propagates without changing its quantum numbers.

Higher-order contributions are terms that represent correlations between the initial and final ph states, and terms that dress the non-interacting single-particle (sp) propagators. Both types of corrections are included in the first-order contribution given by

$\pi ^{(1)}(\alpha ,\beta ^{-1};\gamma ,\delta ^{-1};t-t')$ $=(-{\frac {i}{\hbar }})^{2}\int _{-\infty }^{\infty }dt_{1}{\frac {1}{4}}\sum _{\kappa \lambda \mu \nu }^{}\langle \kappa \lambda |V|\mu \nu \rangle \langle \phi _{o}^{N}|T[a_{\kappa }^{+}(t_{1})a_{\lambda }^{+}(t_{1})a_{\nu }(t_{1})a_{\mu }(t_{1})a_{\bar {\beta }}^{+}(t)a_{\alpha }(t)a_{\gamma }^{+}(t')a_{\bar {\delta }}(t')]|\phi _{o}^{N}\rangle$ (Eq. 7)

in the time formulation. A scheme to calculate excited states using non-interacting sp propagators can be obtained by keeping only those terms in Eq. (7) which link the propagators. Since $V$ is symmetric, one has

$\pi ^{(1)}(\alpha ,\beta ^{-1};\gamma ,\delta ^{-1};t-t')\rightarrow (i\hbar )^{2}\int _{-\infty }^{\infty }dt_{1}\sum _{\kappa \lambda \mu \nu }^{}\langle \kappa \lambda |V|\mu \nu \rangle G^{(o)}(\alpha ,\kappa ;t-t_{1})G^{(o)}(\mu ,{\bar {\beta }};t_{1}-t)G^{(o)}(\nu ,\gamma ;t_{1}-t')G^{(o)}({\bar {\delta }},\lambda ;t'-t_{1})$ (Eq. 8)

Fig.9

Fig.10

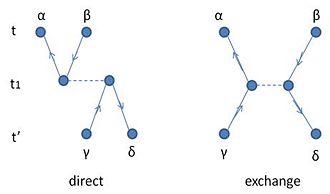
as shown in Fig. 9. The physical meaning of this expression is that a ph pair is added at time $t'$ with quantum number $\gamma \delta ^{-1}$, and then propagates to $t_{1}$. At this momentan interaction changes the prapagation to a ph pair with quantum number $\alpha \beta ^{-1}$ which ends at $t$ when the pair is removed. The Fourier transform of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{(1)} } is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{(1)} (\alpha, \beta^{-1}; \gamma, \delta^{-1}; E) = \pi^{(o)} (\alpha, \beta^{-1}; E) \langle \alpha \beta^{-1} | V_{ph} | \gamma \delta^{-1} \rangle \pi^{(o)} (\gamma, \delta^{-1}; E) } (Eq. 9)

which is shown in Fig. 10. Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{0}(\alpha, \beta^{-1};E) } is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{(1)} (\alpha, \beta^{-1}; \gamma, \delta^{-1}; E) } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \int \frac{dE'}{2 \pi i} G^{(o)}(\alpha, \gamma; E+E')G^{(o)}(\bar{\gamma}, \bar{\beta}; E') = \delta_{\alpha, \gamma} \delta_{\beta, \delta} \pi^{(o)}(\alpha, \beta^{-1}; E) }

Equation (9) can be cast into the form

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{(o)} (\alpha, \beta^{-1}; E) \langle \alpha \beta^{-1} | V_{ph} | \gamma \delta^{-1} \rangle \pi^{(o)} (\gamma, \delta^{-1}; E) }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \pi^{(o)} (\alpha, \beta^{-1}; E) \sum_{\epsilon \theta} \langle \alpha \beta^{-1} | V_{ph} | \epsilon \theta^{-1} \rangle \pi^{(o)} (\epsilon, \theta^{-1}; \gamma, \delta^{-1}; E) }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow \pi^{(o)} (\alpha, \beta^{-1}; E) \sum_{\epsilon \theta} \langle \alpha \beta^{-1} | V_{ph} | \epsilon \theta^{-1} \rangle \pi^{RPA} (\epsilon, \theta^{-1}; \gamma, \delta^{-1}; E) }

When this expression is included to the non-interacting polarization propagator, one obtains the corresponding approximation to the exact polarization propagator, in which the ph interaction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{ph} } is iterated to all orders with the non-interacting polarization propagator. Schematically,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{RPA} = \pi^{(o)} + \pi^{(o)} V_{ph} \pi^{(o)} + \pi^{(o)} V_{ph} \pi^{(o)} V_{ph} \pi^{(o)} + \pi^{(o)} V_{ph} \pi^{(o)} V_{ph} \pi^{(o)} V_{ph} \pi^{(o)} + ... }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \pi^{(o)} + \pi^{(o)} V_{ph} [\pi^{(o)} + \pi^{(o)} V_{ph} \pi^{(o)} +\pi^{(o)} V_{ph} \pi^{(o)} V_{ph} \pi^{(o)} + ... ] }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \pi^{(o)} + \pi^{(o)} V_{ph} \pi^{RPA} }

Explicitly,

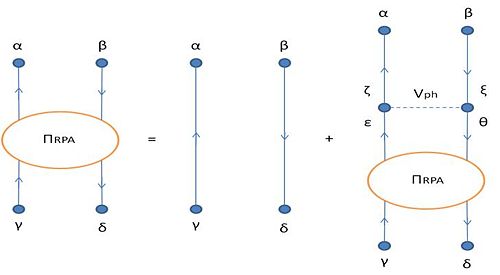
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{RPA} (\alpha, \beta^{-1}; \gamma, \delta^{-1}; E) = \pi^{(o)} (\alpha, \beta^{-1}; \gamma, \delta^{-1}; E) + \pi^{(o)} (\alpha, \beta^{-1}; E) \sum_{\epsilon \theta} \langle \alpha \beta^{-1} | V_{ph} | \epsilon \theta^{-1} \rangle \pi^{RPA} (\epsilon, \theta^{-1}; \gamma, \delta^{-1}; E) } (Eq. 10)

or

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{RPA} (\alpha, \beta^{-1}; \gamma, \delta^{-1}; E) = \pi^{(o)} (\alpha, \beta^{-1}; \gamma, \delta^{-1}; E) + \sum_{\epsilon \theta \zeta \xi} \pi^{(o)} (\alpha, \beta^{-1}; \zeta, \xi^{-1}; E) \langle \alpha \beta^{-1} | V_{ph} | \epsilon \theta^{-1} \rangle \pi^{RPA} (\epsilon, \theta^{-1}; \gamma, \delta^{-1}; E) } (Eq. 11)

Fig.11 Diagrammatic representation of Eq. 11.

Fig.12 Diagrammatic representation of a few higher order diagrams generated by Eq. 11. Only the direct contribution (the dashed line) to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{ph} } is employed.

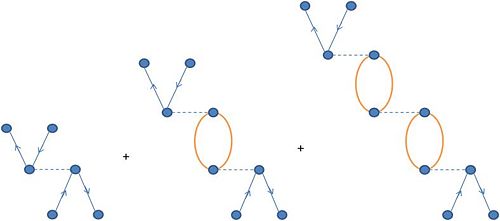
As shown in Fig. 11, successively replacing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{RPA} } generates higher order terms in which the unperturbed ph propagator is interrupted zero, one, two, three, ect. many times by the action of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{ph} } .

As shown in Fig.12, when the direct contribution to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{ph} } is used to generate higher-order terms, the bubbles or rings emerge when the direct part of the interaction is used to connect the unperturbed ph propagation. Each bubble represents the sum of a forward- and backward-going term corresponding to the first or second term in Eq. (6), respectively. The existence of both terms implies interplay between the components when Eq. (11) is solved. It generates the possibility of intermediate states in which many ph states are present at the same time. It has been argued that these Pauli exchange terms add up with random phases and might therefore be rather small, hence the name random phase approximation (RPA).

RPA in Finite Systems and the Schematic Model

To solve Eq. (10) we assume that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{RPA} } also has a Lehmann representation, like the non-interacting and the exact propagator. For RPA, define

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{\alpha \beta}^{n} = \langle \psi_{n}^{N} | a_{\alpha}^{+} a_{\bar{\beta}} | \psi_{n}^{N} \rangle^{*} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_{\alpha \beta}^{n} = \langle \psi_{n}^{N} | a_{\bar{\beta}}^{+} a_{\alpha} | \psi_{n}^{N} \rangle^{*} = - X_{\bar{\beta} \bar{\alpha}}^{n} }

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{n}^{\pi} = E_{n}^{N} - E_{o}^{N} }

Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{RPA} } in Lehmann representation is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi^{RPA}(\alpha, \beta^{-1}; \gamma, \delta^{-1}; E) = \sum_{n \neq 0}^{} \frac{X_{\alpha \beta}^{n} X_{\gamma \delta}^{n *}}{E - \epsilon_{n}^{\pi}+i \eta} - \sum_{n \neq 0}^{} \frac{Y_{\alpha \beta}^{n *} Y_{\gamma \delta}^{n}}{E + \epsilon_{n}^{\pi}-i \eta} } (Eq. 12)

In case of a finite system, we consider bound states and the summation in Eq. (12) involves some discrete states. Taking the limit

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{E \rightarrow \epsilon_{n}^{\pi}} (E - \epsilon_{n}^{\pi}) [\pi^{RPA} = \pi^{(o)} + \pi^{(o)} V_{ph} \pi^{RPA}]}

one has

$X_{\alpha \beta }^{n}X_{\gamma \delta }^{n*}=0+\pi ^{(o)}(\alpha ,\beta ^{-1};\epsilon _{n}^{\pi })\sum _{\epsilon \theta }^{}\langle \alpha \beta ^{-1}|V_{ph}|\epsilon \theta ^{-1}\rangle X_{\epsilon \theta }^{n}X_{\gamma \delta }^{n*}$

$X_{\alpha \beta }^{n}=\pi ^{(o)}(\alpha ,\beta ^{-1};\epsilon _{n}^{\pi })\sum _{\epsilon \theta }^{}\langle \alpha \beta ^{-1}|V_{ph}|\epsilon \theta ^{-1}\rangle X_{\epsilon \theta }^{n}$ (Eq. 13)

Using Eq. (6) the equation above for $\alpha >F>\beta$ can be written as

$[\epsilon _{n}^{\pi }-(\epsilon _{\alpha }-\epsilon _{\beta })]X_{\alpha \beta }^{n}=\sum _{\epsilon \theta }^{}\langle \alpha \beta ^{-1}|V_{ph}|\epsilon \theta ^{-1}\rangle X_{\epsilon \theta }^{n}$ (Eq. 14)

whereas for $\alpha <F<\beta$ one has

$[\epsilon _{n}^{\pi }+(\epsilon _{\beta }-\epsilon _{\alpha })]X_{\alpha \beta }^{n}=-\sum _{\epsilon \theta }^{}\langle \alpha \beta ^{-1}|V_{ph}|\epsilon \theta ^{-1}\rangle X_{\epsilon \theta }^{n}$ (Eq. 15)

Now, we further assume that the ph interaction is separable, that is,

$\langle \alpha \beta ^{-1}|V_{ph}|\epsilon \theta ^{-1}\rangle =\lambda Q_{\alpha \beta }Q_{\epsilon \theta }^{*}$ (Eq. 16)

where $\lambda$ is the coupling constant and $|Q_{\alpha \beta }|=|Q_{\beta \alpha }|$. Substituting this into Eq. (14) yields

$[\epsilon _{n}^{\pi }-(\epsilon _{\alpha }-\epsilon _{\beta })]X_{\alpha \beta }^{n}=\lambda Q_{\alpha \beta }\sum _{\epsilon \theta }^{}Q_{\epsilon \theta }^{*}X_{\epsilon \theta }^{n}$

for $\alpha >F>\beta$. This implies that

$X_{\alpha \beta }^{n}=C{\frac {Q_{\alpha \beta }}{\epsilon _{n}^{\pi }-(\epsilon _{\alpha }-\epsilon _{\beta })}}$ (Eq. 17)

where

$C=\lambda \sum _{\epsilon \theta }^{}Q_{\epsilon \theta }^{*}X_{\epsilon \theta }^{n}$ (Eq. 18)

Similarly, for $\alpha <F<\beta$ we have

$X_{\alpha \beta }^{n}=-C{\frac {Q_{\alpha \beta }}{\epsilon _{n}^{\pi }-(\epsilon _{\alpha }-\epsilon _{\beta })}}$ (Eq. 19)

Inserting Eqs. (17) and (19) into Eq. (18) leads to

$C=\lambda \sum _{\epsilon >F>\theta }^{}{\frac {C|Q_{\epsilon \theta }|^{2}}{\epsilon _{n}^{\pi }-(\epsilon _{\epsilon }-\epsilon _{\theta })}}-\lambda \sum _{\epsilon <F<\theta }^{}{\frac {C|Q_{\epsilon \theta }|^{2}}{\epsilon _{n}^{\pi }-(\epsilon _{\epsilon }-\epsilon _{\theta })}}$

${\frac {1}{\lambda }}=\sum _{\epsilon >F>\theta }^{}{\frac {|Q_{\epsilon \theta }|^{2}}{\epsilon _{n}^{\pi }-(\epsilon _{\epsilon }-\epsilon _{\theta })}}-\sum _{\epsilon <F<\theta }^{}{\frac {|Q_{\epsilon \theta }|^{2}}{\epsilon _{n}^{\pi }-(\epsilon _{\epsilon }-\epsilon _{\theta })}}$ (Eq. 20)

This is an eigenvalue equation which can be solved schematically. For simplicity, let us ignore the second term (hp) and consider the first (ph) term only (called Tamm-Dancoff approximation, TDA), that is,

${\frac {1}{\lambda }}=\sum _{\epsilon >F>\theta }^{}{\frac {|Q_{\epsilon \theta }|^{2}}{\epsilon _{n}^{\pi }-(\epsilon _{\epsilon }-\epsilon _{\theta })}}$ (Eq. 21)

Fig.13 Graphical solution of Eq. 21

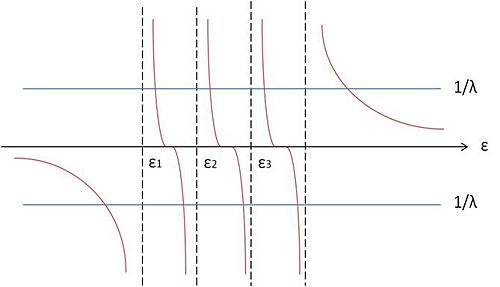
As shown in Fig. 13, the curve is the right side of Eq. (21) as a function of $\epsilon _{n}^{\pi }$, whose poles are indicated by the vertical asymptotes. For repulsive interaction ($\lambda >0$), the energies are bound between the poles, except for the largest one. If the interaction is very small, all the energies are close to those for non-interacting case, as expected. On the other hand, if the interaction is very large all the energies deviate from the non-interacting ones. In particular, the highest shifts upward a lot. The states with energies bound between the poles are close to the eigenstates for the non-interacting Hamiltonian with tiny admixture with each other. However, the state of the highest energy is a coherent superposition of all the non-interacting eigenstates, in which each non-interacting eigenstate contributes almost the same amount. Similar situation happens for attractive interaction ($\lambda <0$). In this case, when the coupling constant is very large, there is a state which mixes all the non-interacting eigenstates almost equally and its energy is lowered greatly. Such coherent states correspond to the collective modes of the system.

As mentioned in Sec. 2, examples of the collective mode are the giant resonance. The best known and the most thoroughly investigated giant resonance is the giant dipole state, excited, for instance, by photo-absorption of $\gamma$-radiation [8]. It is a several MeV broad resonance, which has been observed over the whole periodic table. A typical case is shown in Fig. 5. The experimental spectrum usually shows fine structure. It has its origin in the specific properties of nuclei and is not constant over the periodic table. Particular ph components may show up - as in O-16 [9] - or shell effects may cause a splitting of the resonance. The structure of the dipole operator shows that the giant dipole resonance consists mainly of $1\hbar \omega$ excitations. Because of the repulsive character of the residual interaction it is shifted to higher energies.

Reference

[1] A. Fetter and J. Walecka, Quantum Theory of Many-Particle Systems, Dover, 2003

[2] M. Mayer and J. Jensen, Elementary Theory of Nuclear Shell Structure, John Wiley and Sons, 1955

[3] P. Ring and P. Schuck, The Nuclear Many-Body Problem, Study ed, Springer, 2004

[4] R. Bramblett, J. Caldwell, R. Harvey, and S. Fultz, Phys. Rev. 133 (1964) B869. 281

[5] L. Malov and V. Nesternko, and V. Soloviev, Phys. Lett. 64B (1976) 247. 292, 345

[6] S. Stringari, Nucl. Phys. A325 (1979) 199. 292, 337, 339, 563

[7] W. Dickhoff and D. Van Neck, Many-Body Theory Exposed!, 2nd ed, World Scientific, 2008

[8] B. Spicer, Adv. Nucl. Phys. 2 (1969) 1. 293

[9] J. Elliott and B. Flowers, Proc. Roy. Soc. (London) A242 (1957) 57. 174, 293, 325, 326