Scaling theory of localization
localization
Before 1958, there was an traditional view about the behavior of an electronic system whit a random potential. The traditional view had been that scattering by the random potential causes the Bloch waves to lose phase coherence on the length scale of the mean free path Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} . Nevertheless, the wave function remains extended throughout the sample. In 1958 Anderson proposed that the electronic systems maybe altered significantly if the disorder level is very strong. That means if we add a strong random potential to system,the wave function may become localized, and the wave function decays exponentially around the random center in space,i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid\psi(\overrightarrow{r})\mid\sim exp(\mid\overrightarrow{r}-\overrightarrow{r}_{0}\mid/\xi)} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} is the localization length.
The existence of the localized state is easily understood if we work in the limit of very strong disorder. Then a zeroth order description of the wave functions would be a bound state or a localized function by strong fluctuation in the random potential. We could then consider the admixture between different orbitals as a perturbation. The point that we should consider is that such admixtures will not produce an extended state composed of linear combination of infinitely many localized states. That is because that orbitals that are nearby in space,so that they overlap significantly, are in general very different in energy, so that the admixture is small since there is a large energy difference in denominator. on the other hand,orbitals that are nearly degenerate are in general change far apart in space, so that the overlap is exponentially small. So in the strong disorder limit, the wave function will be exponentially localized.
We could see the admixture between different orbitals will not produce an extended state because the nearby orbitals have large differences in energy and the orbitals that have the same energy are far apart in space. In both cases next order perturbation has small value and does not alter the localized states significantly.
If we ignore electron-electron and electron-phonon interactions, then in one dimension, all states are localized and it is not important how weak the disorder is. In two dimensions, they have the same behavior but in three dimensions it depends on the disorder level. That means we can have a transition between a metal and an insulator if we increase the disorder level. For weak disorder we have still extended states in the spectrum (in 3D). The dividing line between localized and extended states in the energy spectrum is called the mobility edge that is a function of disorder strength Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w} .
Here we introduce the localization length as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi^{-1}\equiv\underset{m\rightarrow\infty}{lim}\frac{-1}{2m}Ln\overline{\mid<0\mid G\mid m>\mid^{2}}}
Where the bar means the average over the random potentials on each site, and G is the Green's function for system. Also Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid m>}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid 0>}
are the position eigenstates so that we assume the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid 0>}
at the disorder site. Why we introduce the localization length in this form? Assume the disorder site has energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon}
and the wave function falls off exponentially as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle exp(\frac{-m}{\xi}}
), where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m}
is the distance from the peak. So we can calculate Green's function as below:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <m\mid G(\varepsilon-i\eta)\mid0>=\sum_{n}\frac{<m\mid\varepsilon_{n}><\varepsilon_{n}\mid0>}{\varepsilon-\varepsilon_{n}-i\eta}}
Because the peaks of the wave function move about randomly, only a small fraction of the wave functions, order l/N where N is the number of sites in the lattice, will be peaked at 0; the rest will be negligible because their overlap with site 0 is so small. So
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <m\mid G(\varepsilon-i\eta)\mid0>=V\int d\varepsilon^{'}D(\varepsilon^{'})\frac{<m\mid\varepsilon_{n}><\varepsilon_{n}\mid0>}{\varepsilon-\varepsilon_{n}-i\eta}\thickapprox\frac{V\xi}{N}D(\varepsilon)i\pi<m\mid\varepsilon>}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D(\varepsilon)}
is density of function at energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon}
and V is volume of considered system.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <m\mid G(\varepsilon-i\eta)\mid0>\thickapprox\frac{V\xi}{N}D(\varepsilon)i\pi e^{i\phi}e^{-\frac{m}{\xi}}}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} describes the phase of the matrix element. As you can see by using of the definition for the localization length we can get good result for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} because we we calculate average over all random possibilities the phaseFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\phi)} goes to zero.
Scaling Theory of Localization
The most applicable method to describe localization is a scaling theory that it was proposed by Abrahams et.al.(1979). The physical idea behind this theory is very simple. The hypothesis of the scaling theory is that there is only one function R(l), and the resistance of every quantum resistor changes with length according to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R(l)=R(\frac{l}{l_{0}})} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_{0}} is the length of sample that its resistance is equal to the basic quantum of resistance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{H}: R_{H}\equiv\frac{h}{e^{2}}=25.813\Omega} . In other words, suppose one knows the function R(l); Then whatever material one takes, it is enough to measure the resistance of one sample, and then the resistance of a sample of any other length is known.
In another notation we can say there is a function for the conductance as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g=F(\frac{L}{\xi})} that the function F is called scaling function. In this definition the correlation length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\xi} ) includes all microscopic length scales such as the Fermi wave number,mean free path etc, so this function is a single parameter scaling and these scales do not enter explicitly in the formula. We can guess the shapes of this scaling function by studying its behavior in small and large disorder. In small disorder level or very weak resistors, only occasional scattering sites cause resistivity and so in this limit they should obey the familiar macroscopic Ohm's law. That means in dimension d, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g\sim L^{d-2}} when R is near zero. Also in very large resistance, we expect all states to be localized and the resistivity to rise exponentially with sample length as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g\sim e^{-A_{d}L/L_{0}}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{d}} is a coefficient independent of length and only depend on dimensionality.
Abrahams proposed that instead of making guess about the shapes of g it is better to focus on the function[2]
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta(g)\equiv\frac{dLng}{dLnL}}
So in small g, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta(g)\rightarrow} d-2 and for large g it goes to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ln(\frac{g}{g_{0}})} . Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_{0}} is some constant, and also it should be noticed the dimensionless conductance g in this formula is a suitable average, such as the Thouless conductance or the typical conductance. The typical value of g is defined as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{typ}=exp(<log\rho(x)>)} .
Moreover, you can see the beta function is only function of g. If we assume a monotonic interpolation between these limits we can draw the schematic of the beta function.
Some important result from the behavior of the beta function:
1- In one and two dimension, the function is always negative. So in large sizes we will have no conductance or it will become very small, and we can conclude that all electronic states are localized in these dimensions. But in 2D, the situation is sensitive to our assumption on the monotonic behavior of function because if we consider the spin orbit interaction the function will become non-monotonic and we have a transition in 2D in some circumstances such as very strong the spin-orbit interaction.
2- In 3D, the beta function has zero value for a value of the conductance. This point is related to a phase transition between insulator and metal. This transition is called the Anderson transition. Also for conductance larger than a critical value, making a system larger continually decrease its resistance, and for smaller than this value it behaves inversely.
We can conclude the scaling theory makes easy to determine localization. That means rather than studying any properties of wave function or any Hamiltonian,we focus on how the solution changes with change of scale. So if we have the behavior of any sample for different scales we can say there is any localization or not. If the conductance increases with making larger it behaves like metallic phase and inversely if it decreases it behaves like insulating phase.
For example in below figure there is a transition between metals and insulators at a disorder w of around 17 because larger than this value the resistance increases with making system larger.
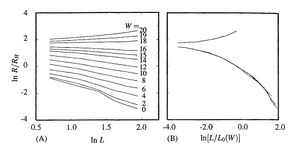
Method Description And My Numerical Results
I used transfer matrix method to calculation the conductance for one dimension, but there are some other methods like Green's function that one should use Hamiltonian to build up Green's function and then try to calculate its inverse numerically. In transfer matrix method we consider a tight binding model for a one dimension chain as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{l}U_{l}\mid l><l\mid+t\mid l><l+1\mid+t\mid l+1><l\mid}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{l}} is a random variable for a disorder system. Here we choose a uniform distribution for U between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{w}{2}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{w}{2}} . So we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\mid\psi>=E\mid\psi>\Rightarrow U_{l}\mid l>\psi_{l}+t\mid l>\psi_{l+1}+t\mid l+1>\psi_{l}=E\mid\psi>}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{l}\psi_{l}+t\psi_{l+1}+t\psi_{l-1}=E\psi_{l}\Rightarrow(\begin{array}{c} \psi_{l+1}\\ \psi_{l}\end{array})=(\begin{array}{cc} \frac{E-U_{l}}{t} & -1\\ 1 & 0\end{array})(\begin{array}{c} \psi_{l}\\ \psi_{l-1}\end{array})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M=\left(\begin{array}{cc} \frac{E-U_{l}}{t} & -1\\ 1 & 0\end{array}\right)}
where M is the real-space transfer matrix. Then we can calculate total transfer matrix and calculate another transfer matrix that relate amplitudes of incident and scattered waves(T) as below:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T=V^{-1}MV } (see Appendix A)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=\left(\begin{array}{cc} 1 & 1\\ \lambda^{-1} & \lambda\end{array}\right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=\frac{1}{2}(x+\sqrt{x^{2}-4})}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\frac{E-U_{l}}{t}} . By taking the energy E as arbitrary parameter we can calculate T matrix and then compare it to the general matrix we can get transmission probability equal square of first element. By using of Landauer formula (see Appendix B) we can calculate conductance:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g= T_{p}=\mid T_{11}\mid^{2}}
Where is transmission probability and is the first element of transfer matrix. It should be notice that total conductance is and here we used typical value of conductance as g.
.png)
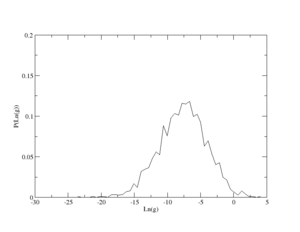
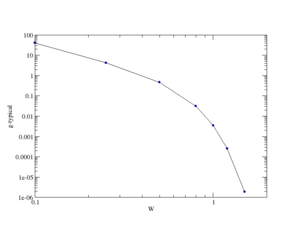
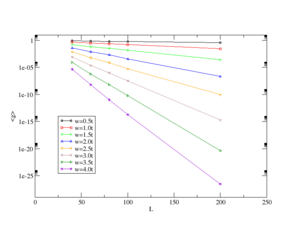
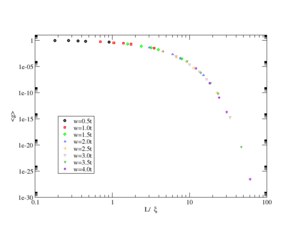
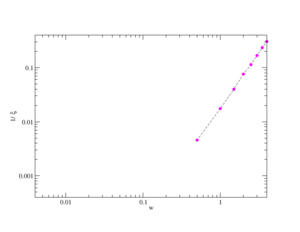
The Anderson transition
As we said at the transition the beta function is zero and so the conductance is independent of the system size. So by using of scaling function we conclude that the correlation length diverges at this point. In 1985 Lee and Ramakrishnan proposed this divergence behaves asFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi\sim\mid x-x_{c}\mid^{-\nu}} where x is a parameter that is used to drive the system through the transition like carrier density or impurity concentration and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{c}} is the critical value.
So the conductivity also has a power law dependence close to the transition Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g\sim L^{d-2}(x-x_{c})^{s}} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x>x_{c}} . Also for small value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\frac{L}{\xi}} the scaling function behaves as a power law Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x)\sim x^{\eta}} . Because g is independent of L we can conclude Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta=d-2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s=(d-2)\nu} . This is called Wegner's scaling relation.
As you can see in 2D at the transition s=0, so the conductivity remains finite at the Anderson transition and decreases to zero discontinuously in the insulting phase.
One of the important features of critical phenomena is that the values of the exponents exhibit universality. Their values depend only on the dimensionality of the system and symmetry of the system. For the Anderson transition the relevant symmetries are time reversal symmetry and spin-rotation symmetry (Hikami 1981). In fact, there is an exact correspondence with the symmetry classes that occur in the theory of random matrices (Mehta 2004): the “orthogonal” class with both time reversal symmetry (TRS) and spin-rotation symmetry (SRS), the “unitary” class where TRS is broken, and the “symplectic” class with TRS but where SRS is broken.
Appendix A: Connection Between T and M(Two Different Transfer Matrices)
Note that the transfer matrix M, does not hav ethe structure of the transfer matrix T. Indeed, T connects the propagating waves on the left and right hand side of the sample, while M relates the wave function in the site representation. Both matrices are connected as follows:
We can write down a wave function between two sites n-1 and n as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{n}(x)=A_{n}e^{ikx}+B_{n}e^{-ikx}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \psi_{n}(0)=a_{n}=A_{n}+B_{n}\\ \psi_{n}(-1)=a_{n-1}=A_{n}e^{-ik}+B_{n}e^{ik}\end{cases}}
where we assume the origin(x=0) at nth site, and also for simplicity we use the lattice constant as the unit length. Here k is the Bloch wave vector and because the reference system supports a set of Bloch waves defined by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\begin{pmatrix} \psi _{n+1}\\ \psi _{n} \end{pmatrix}=\begin{pmatrix} \psi _{n+2}\\ \psi _{n+1} \end{pmatrix}=e^{ik}\begin{pmatrix} \psi _{n+1}\\ \psi _{n} \end{pmatrix}}
and we conclude Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ik}} is an eigenvalues of M So by solving for the eigenvalue of M we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ik}=\lambda=e^{ik}=\frac{1}{2}(x+\sqrt{x^{2}-4})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\frac{E-U_{l}}{t}}
So, we can write these relationships in a matrix form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} a_{n}\\ a_{n-1}\end{array}\right)=\left(\begin{array}{cc} 1 & 1\\ e^{-ik} & e^{ik}\end{array}\right)\left(\begin{array}{c} A_{n}\\ B_{n}\end{array}\right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} A_{n}\\ B_{n}\end{array}\right)=\frac{1}{2iSinK}\left(\begin{array}{cc} e^{ik} & -1\\ -e^{-ik} & 1\end{array}\right)\left(\begin{array}{c} a_{n}\\ a_{n-1}\end{array}\right)}
By using of this result and also
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{array}{c} A_{n+1}\\ B_{n+1}\end{array}\right)=T_{n}\left(\begin{array}{c} A_{n}\\ B_{n}\end{array}\right) }
we can get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V^{-1}\begin{pmatrix} \psi _{n+1}\\ \psi _{n} \end{pmatrix}=T_{n}V^{-1}\begin{pmatrix} \psi _{n}\\ \psi _{n-1} \end{pmatrix}}
Where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=\left(\begin{array}{cc} 1 & 1\\ \lambda^{-1} & \lambda\end{array}\right)}
Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} \psi _{n+1}\\ \psi _{n} \end{pmatrix}=VT_{n}V^{-1}\begin{pmatrix} \psi _{n}\\ \psi _{n-1} \end{pmatrix}}
So from the difinition of M, we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M=VT_{n}V^{-1}} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T=V^{-1}MV}
Appendix B: B. Landauer formula
Here we want to derive the Landauer formula in 1D(see forther details in ref.):
Consider a single transverse mode whose +k states are occupied according to some function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{+}(E)} . A uniform electron gas with n electrons per unit length moving with a velocity v carries a current equal to env. Since the electron density associated with a single &-state in a conductor of length L is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{L}} we can write the current Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I^{+}} carried by the +k states as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I^{+}=\sum_{k}en(k)vf^{+}(E)=\frac{e}{L}\sum_{k}\frac{1}{\hbar}\frac{\partial E}{\partial k}f^{+}(E) } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=\frac{1}{\hbar}\frac{\partial E}{\partial k}} by considering a periodic boundry conditions for our wire.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k}\rightarrow2(spin)\times\frac{L}{2\pi}\int dk I^{+}=\frac{2e}{h}\ \int_{\varepsilon}^{\infty}f^{+}(E)dE}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} is the cut-off energy of the wave guide mode.The leads are assumed to be ballistic conductors, each having M transverse modes. T is the average probability that an electron injected in lead 1 will transmit to lead 2. And also we assume the contacts are 'reflectionless'. For multi-moded wave guide we will have
So, the total current for one mode is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I=I^{+}-I^{-}=\frac{2e}{h}[\int_{-\infty}^{+\infty}(f_{1}(E)-f_{2}(E))dE] \cong\frac{2e}{h}[\int_{-\infty}^{+\infty}-\frac{\partial f}{\partial E}(\mu_{1}-\mu_{2})M(E)T(E)dE] \rightarrow G=\frac{2e^{2}}{h}[\int_{-\infty}^{+\infty}-\frac{\partial f}{\partial E}M(E)T(E)dE]}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cong\frac{2e^{2}}{h}\overline{MT}}
Where we assume the low temperature and small voltage for simplify the integral by subtituting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{+}(E)-f^{-}(E)\cong-\frac{\partial f}{\partial E}(\mu_{1}-\mu_{2})} and using of . As you can see there is no dependence on the lenght of wire in this relationship.
References
1. Patric A. Lee, T. V. Ramakrishnan, Reviews of Modern Physics, Vol.57,No. 2(1985).
2. E. Abrahams, P. W. Anderson, et al, Physical Review Letters 42, 10, 673(1979).
3. Michael P. Marder,"Condensed Matter Physics" book,A Wiely-Interscience Publication, John Wiley& sons Inc., New york(1999).
4. S. Datta, "Electronic transpot in mesoscopic systems", Cambrifge; New york, Cambridge University Press(1995).
5. A. Mackinnon, B. Kramer, Physical review Letters 47,21, 1546(1981).