Self-organized criticality and earthquakes
In 1987 the team of Bak, Tang, and Weisenfeld presented a paper on "Self-organized Criticality" which hoped to provide a very simplified model to explain the complexity that is found in nature. Prior to this, many models describing complex systems had been developed however there was no general theory of complexity built on a strong mathematical foundation. The theory with which the team attempted in their paper explains the "self-organized critical state" (SOC) by comparing it to that of a steep sand pile which emits avalanches of all sizes as more sand is added to the system. This state is characterized by the fact that the system has self-organized itself to a point where it is on the border between predictability and unpredictability to the so called "edge of chaos." For the specific case of earthquakes, it can be postulated that the crust of the earth is a highly self-organized system which features earthquakes that are unpredictably strong, where the intensity and frequency of the quakes follow a power law distribution. Power law distributions are a key aspect of SOC.
Some of the criticisms of the theory include that it does not mathematically show why the critical systems follow a power law distribution and it also does not explain why the systems self organize.
The Sandpile Paradigm
Consider a pile of sand of any size. As sand is added to the pile(at any position not just limited to the center) the size and slope of the pile will become larger and larger. Soon it will reach a slope where the addition of more sand will trigger avalanches that will increase in size as the slope of the pile also increases in size. Eventually this slope will reach a particular size where it will no longer increase due to the fact the amount of sand added will balance out with the amount of sand leaving the pile. This is known as the critical stationary state of the sandpile. At this point the individual dynamics of each grain of sand is not as important as a new emergent dynamic of the sandpile has become global. Any perturbation made to the system may cause avalanches that are either large or small perhaps causing the physical appearance of the sandpile to change but this system dynamic will remain complex. The same perturbation that might cause a small avalanche could also cause a large avalanche.
The Sandpile Model

The best way to understand this is to consider a very simple model which can be easily recreated and simulated using a computer. Imagine a sandpile with equal sized sand granules that have no imperfections (to simplify the interaction between each sand granule and the ones next to it. As Bak puts it this is "theoretical physicist's sand". Sand is then randomly added to a site in the growing pile and thus increasing its height. When a particular site becomes too high it will distribute the sand at that site to the 4 adjacent sites around it. So if the highest a particular site can reach is 4 units of sand then those 4 units will be taken away from that site and 1 will be given to each of the 4 adjacent sites.
To better understand what is occurring refer to the very useful applet that was created by Maslov.
One of the significant features of the model is that it does not matter what the initial state of the sandpile is in when the experiment begins or where the sand happens to be randomly added to. If all that is known about the beginning state of the pile is that each site has less than 3 units of sand (the maximum before an 'avalanche' occurs) then we know that there are no immediate unstable sites. No avalanches will take place until a site reaches 4 units of sand in which case it will topple to the adjacent sites. If that causes one of the adjacent sites to have more than 3 units of sand then that site will also topple and so on until the avalanche resolves itself and all of the sites are back down to 3 or less units of sand. With units of sand continuing to be added to the system after the avalanches, eventually the system will reach the stationary state that was mentioned before. Figure 3 on the left also shows the result of the domino effect that takes place when an avalanche begins.
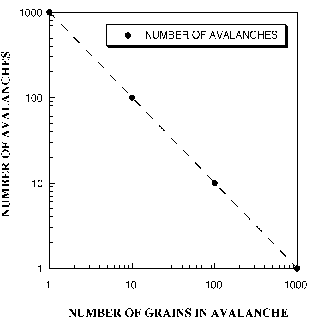
After using the sand pile applet and noticing the that occur in the final states of the sand pile we notice that the avalanches have caused a fractal to form into the sand pile a lot like the fractals which are found along Norway's coast.
The 'edge of chaos' and power law distributions
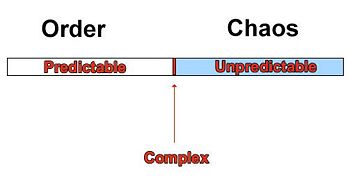
Systems which have self organized into the critical state (complexity) are at the boundary between order and chaos. These systems then have fluctuations which follow a power law distribution.
Power law distribution in the sand pile model
Avalanches in the sand pile model follow the very simple power law: Graphing the logs of the intensity of the avalanches which occur in the sand pile model in relation to the logarithm of their frequencies one obtains a power law distribution which looks like the following:
At the boundary, "The Edge of Chaos"
Systems that are complex like those found in nature are systems that have self-organized regardless of the state in which they began organizing. These systems tune themselves to a critical point where power law behavior is seen. A relevant comparison to a topic in our class is looking at the critical point in the phase transition diagram located at the top of the transition line between liquid and gas. At this critical point a continuous phase transition can be made from a gas state to a liquid state. As it approaches the critical point it makes a transition into a super critical fluid which basically has gas bubbles and liquid together and the size and frequency of the gas bubbles depends on the pressure and density. If however the sample is placed directly at the critical point the size and frequency of the gas bubbles are scale invariant and follow a power law distribution[4]. One of the best examples for SOC's application to nature in the real world (and one that Bak is proud of) is in its insight to the topic of geology, specifically that of earthquakes. The power law distribution found in the Gutenberg-Richter law is an important aspect to the comparison.
The crust of the Earth is in a self-organized critical state
It can be thought of that after 100's of millions of years the crust of the Earth has self organized itself into a critical state. The combination of plate tectonics, earthquake dynamics, volcanic activity and other types landscape formation have culminated in the critical state of the crust which we see today. The organization is seen by things such as the rivers, faults, and rock patterns on the surface. The fractal design of Norway's coast is a good example of how Self-organizing criticality has taken place in the formation of our landscape. The result of our crust being in a highly organized critical state are some of the natural phenomenon we observe. Most relevant is the earthquake which rests on the unpredictable side of the 'edge of chaos'. The organization of the crust into the critical state means that earthquakes can happen with unpredictable intensities. The next earthquake could be anything from a rumble to a cataclysmic catastrophe and it is impossible to know for certain what will come because the same organization which can lead to a rumble is the same that could lead to something more powerful.
Spring-slider Block Model
One way to look at the production of an earthquake is to consider the mechanism to function like a spring-slider block model like the one seen to the right. A constantly moving plate is attached to blocks by a 'leaf spring' and the blocks are connected to each other by coil springs. The leaf spring basically represents the pressure due to tectonic plate motion. As the top plate is moving the leaf spring exerts an increasing force on the individual blocks until a threshold is reached and one of the blocks slips a little in the direction of the moving plate. The slipping of one block might cause the slipping of another block due to the increased force from the coil spring until finally a chain reaction is produced which is synonymous with an earthquake occurring. The relevance of this model is that the math for this model is almost identical to that of a coupled pendulum. (a system which we know from mechanics builds up to a chaotic state). In turn Bak also proved that the math for the coupled pendulum is also almost identical to that for the sand pile model which exemplifies his SOC theory. Because of all of this and with independent research from some other groups, earthquakes can be thought of as an SOC phenomenon.
The one major issue with this is that the block spring model is not necessarily a conservative system while the sandpile model which was discussed was conservative. Even with making the necessary adjustments the Gutenberg-Richter law is followed only up to a certain cut-off point meaning only small earthquakes with this model.
The Gutenberg-Richter Law
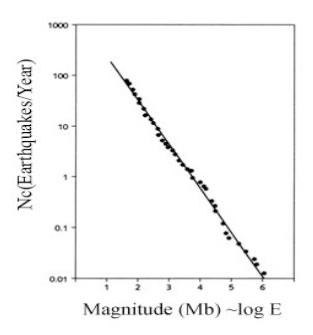
According to Bak, "the Gutenberg-Richter law is the fingerprint that the crust of the earth has self-organized to the critical state."
The Gutenberg-Richter law relates the magnitude of some earthquakes which occur in a particular location with the total number of those earthquakes. The law goes as follows:
or
Where:
- is the number of events in a given magnitude range
- is a magnitude minimum
- and are constants
The implication behind this is that there will be 10 times as many earthquakes of a certain magnitude as there will be for an earthquake with a magnitude of 1 higher. A 5.0 magnitude on the Richter scale will happen 10 times more than a single 6.0 magnitude. The power law distribution can be seen easily in the graph on the right. This is the main reason why Bak refers to the law as being one of the principle fingerprints of SOC phenomena occurring in nature.
Other systems which show SOC-like phenomenon
Besides Earthquakes, the SOC theory could be used to interpret:
Fractals.
Starquakes and Solar Flares.
Black Holes.
Population Extinctions in Ecology.
The Barkhausen Effect in Magnetic Domains.
Female Emotions.
Sources
Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems. Cambridge Lecture Notes in Physics Part 10.
How Nature Works: The Science of Self-Organized Criticality. Per Bak.
Modeling Extinction. M.E.J. Newman, R.G. Palmer. Santa Fe Institute Studies in the Sciences of Complexity.
Introduction to Self-Organized Criticality & Earthquakes by Nathan Winslow. http://www.econ.iastate.edu/classes/econ308/tesfatsion/SandpileCA.Winslow97.htm