Semiconductor Magnetism

motivation

The observation of ferromagnetism in magnetic ion doped II–VI diluted magnetic semiconductors (DMSs), and later in (Ga,Mn)As materials has inspired a great deal of research interest in a field dubbed “spintronics” of late, which could pave the way to exploit spin in addition to charge in semiconductor devices. The main challenge for practical application of the DMS materials is the attainment of a Curie temperature at or preferably above room temperature to be compatible with junction temperatures. Zener's model of ferromagnetism, originally proposed for transition metals in 1950, can explain T C of Ga1− xMnxAs and that of its II-VI counterpart Zn1− xMnxTe and is used to predict materials with T Cexceeding room temperature, an important step toward semiconductor electronics that use both charge and spin..The particular predictions are predicated on the assumption that hole mediated exchange interaction is responsible for magnetic ordering. Among the additional advantages of ZnO- and GaN-based DMSs are that they can be readily incorporated in the existing semiconductor heterostructure systems, where a number of optical and electronic devices have been realized, thus allowing the exploration of the underlying physics and applications based on previously unavailable combinations of quantum structures and magnetism in semiconductors.

Diluted magnetic semiconductors

This family of materials encompasses standard semiconductors, in which a sizable portion of atoms is substituted by such elements, which produce localized magnetic moments in the semiconductor matrix. Usually, magnetic moments originate from 3d or 4f open shells of transition metals or rare earths (lanthanides), respectively, so that typical examples of diluted magnetic semiconductors (DMS) are Cd1-xCoxSe, Ga1-xMnxAs, Pb1-xEuxTe and, in a sense, Si:Er. A strong spin-dependent coupling between the band and localized states accounts for outstanding properties of DMS. This coupling gives rise to spin-disorder scattering, giant spin-splittings of the electronic states, formation of magnetic polarons, and strong indirect exchange interactions between the magnetic moments, the latter leading to collective spin-glass, antiferromagnetic or ferromagnetic spin ordering. Owing to the possibility of controlling and probing magnetic properties by the electronic subsystem or vice versa, DMS have successfully been employed to address a number of important questions concerning the nature of various spin effects in various environments and at various length and time scales. At the same time, DMS exhibit a strong sensitivity to the magnetic field and temperature as well as constitute important media for generation of spin currents and for manipulation of localized or itinerant spins by, e.g., strain, light. Electrostatic or ferromagnetic gates. These properties, complimentary to both non-magnetic semiconductors and magnetic metals, open doors for application of DMS as functional materials in spintronic devices.

magnetic impurities in semiconductors

we can describe the DMS according to the model in which the electron states can divided in to two categories:

(i) localized magnetic d or f shells (ii) extended band states built up of s, p, and some times d atomic orbitals

The starting point for developing a useful predictive model of (III-Mn)V ferromagnetism is understanding of the electronic state with the single Mn impurity in the host lattice. we need to understand the charecter of Mn local moments before we explein how these isolated local moments are coupled. Ao we discuss the property of Mn impurity in GaAs and on the nature of ferromagnetic coupling in (Ga, Mn)As.

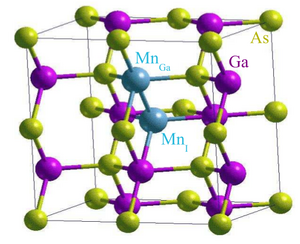
Between (III,V) hosts, Mn impurity has been studied in GaAs. The elements in the (Ga,Mn)As compound have nominal atomic structures:

[Ar]3d10 4s2 p1 for Ga

[Ar]3d5 4s2 for Mn

[Ar]3d10 4s2 p3 for As

This circumstance correctly suggests that the most stable and therefore most common position of Mn in the GaAs host lattice is on the Ga site where its two 4s electrons can participate in crystal bonding in much the same way as the two Ga 4s electrons. The substitutional MnGa , and the less com- mon interstitial MnI , positions are illustrated in Fig. 1. The MnGa impurity can be as an acceptor Because of the missing valence 4p electron. In the electrically neutral state, labeled as A0 (d5 + hole), MnGa has the character of a local moment with zero angular momentum and spin S = 5/2 and a moderately bound hole.Since The local moment is formed by three occupied sp-d bonding states with dominant (3dxy , 3dxz , 3dyz) character and by two occupied

orbitals that are split from the sp-d states by the tetrahe-orientation and together comprise the S = 5/2 local mo- ment. The weakly bound hole occupies one of the three antibonding sp-d levels with dominant As 4p character. The charge −e ionized MnGa acceptor center, labeled as A−(d5 ), has just the S = 5/2 local spin character.

Fig. 1: substitutional MnGa in GaAs.

Abi-initio calculation for Mn in DMS

In SDF theory (Hohenberg and Kohn, 1964; Kohn and Sham, 1965) many-body effects are buried in a complex Sham, 1965) many-body effects are buried in a complex exchange-correlation energy functional. Once an approximation is made for this functional, predictions for electronic and magnetic properties depend only on the particular arrangement of atomic nuclei under consideration The exchange-correlation energy functional leads to a self-consistently determined spin-dependent exchange-correlation potential that appears in an effective independent-particle Hamiltonian. The main technical challenge in DFT applications is the development of numerically efficient methods that provide accurate solutions of single-body Schr¨odinger equations (see review articles (Jones and Gunnarsson, 1989; Sanvito et al., 2002)). DFT Uses the charge density as the fundamental system variable, and describes the ground state properties by using certain functional of the charge density. the advantage of this method is solvingSimply the many body problem by using the electron charge density as fundament variable rather than the wavefunction. However, the major limitation for applying this method is this is only Applicable for the ground state, needs approximation for exchange-correlation energy functional which is unknown.

so, we can apply some successful Approximation for exchange-correlation energy:

LDA

The local density approximation is For regions of a material where the charge density is slowly varying, the local charge density can be considered to be the density of an equivalent uniform homogeneous electron gas. We can produces moderately accurate results in most cases. However, the weakness of this approximation is we cannot predict atomic ground state energies and ionization energies, and overpredicts binding energies.

LSDA

LSDA predictions for spectral properties, like the local DOS, are less reliable than predictions for total-energy related properties. This is especially true for states above the Fermi energy, and is manifested by a notorious in accuracy in predicting semiconductor band gaps. From a DFT point of view, this inconsistency arises from attempting to address the physics of quasiparticle excitations using ground-state DFT. In Mn-doped DMSs, the LSDA also fails to account for strong correlations that suppress fluctuations in the number of electrons in the d shell. One generally accepted consequence is that the energy splitting between the occupied and empty d states is underestimated in SDF theory, leading to an unrealistically large d-state local DOS near the top of the valence band and to an overestimate of the strength of the p-d exchange.

Infact, The many-body effects of the complicated quantum mechanical problem are buried in the so-called exchange-correlation part of the energy functional Ex c [n(r), m(r)]. The exact solution is intractable for macroscopic systems and some approximation must be made.

The local approximation (LSDA) takes as its starting point the energy of a uniformly spin-polarized homogeneous electron gas$\varepsilon _{x,c}(n(r),\left|m(r)\right|)$ so that$E_{x,c}$can be written in the form

$E_{x,c}[n,m]\approx \int drn(r)\varepsilon _{x,c}(n(r),\left|m(r)\right|)$

The functional derivative of this quantity with respect to m(r) provides the effective magnetic fields for the single- electron equations, namely the spin-polarized band structure.

$v^{eff}[n,m;r]=V^{ext}(r)+e^{2}\int dr^{'}{\frac {n(r)}{\left|r-r^{'}\right|}}+{\frac {\delta E_{xc}}{\delta n(r)}}[n,m]$

$B^{eff}[n,m;r]=B^{ext}(r)+{\frac {\delta E_{xc}}{\delta n(r)}}[n,m]$

where$V^{ext}(r)$describes an external potential such as a lattice array of nuclei and $B^{ext}(r)$an external magnetic field. The electron density and magnetization are given by

$n(r)=\int ^{\varepsilon _{f}}d\varepsilon \sum _{i}tr(\varphi _{i}^{\ast }(r,\varepsilon )\varphi _{i}(r,\varepsilon ))$

$m(r)=\int ^{\varepsilon _{f}}d\varepsilon \sum _{i}tr(\varphi _{i}^{\ast }(r,\varepsilon )\sigma \varphi _{i}(r,\varepsilon ))$

where the$\varphi _{i}(r,\varepsilon )$obey the Schrodinger–Pauli [(Kohn– Sham) equation]

$(-\triangledown ^{2}+v^{eff}(r)-\sigma .B^{eff}(r)\varphi _{i}(r,\varepsilon )=\varepsilon \varphi _{i}(r,\varepsilon )$

comparision of magnetic intraction

RKKY intraction

Indirect exchange coupling of magnetic moments over relatively large distance via band electrons due to the Coulomb exchange. It becomes efficient when a high concentration of free carriers is present such as in metals for which it was developed.

Direct superexchange

Direct coupling of magnetic ions through verlap of magnetic orbitals.

Indirect superexchange

Spins of two magnetic ions are correlated due to the exchange interaction between each of the two ions and the valence p-band.

Double exchange

exchange mechanism for the carrier-induced ferromag Couples magnetic ions in different charge state by virtual hopping of the ‘extra’ electron from one ion to the other through interaction with p-orbitals.

Zener model

Zener in 1950 demonstrated that thethe spin coupling between incomplete d shells and condunction electrons leads to the tendency for the ferromagnetic alignment od d spins. The occurance kof ferromagnetism or antiferromagnetism in various system is understood. according to this paper the relative magnitude of three types of coupling determine the type of magnetic behavior. The first coupling arises from the direct exchange between incomplet d shells of nearest neigbors. If we are intrested in the variation of this exchange energy only with the degree of ordering of the net spins of d shells,we can show this energy as ${\frac {1}{2}}\alpha s_{d}^{2}$per atom. here$s_{d}$ is the mean componet per atom of the net spin of the d shells along the direction of magnetization.$\alpha$is positive. so its magnitude rapidly decreases with a decreasing amount of overlap of d shells of adjacent atoms. the second spin coupling arises from the exchange couplingbetween conduction electrons and the inner d electrons. this energy can be represent as $\beta s_{d}s_{c}$ per atom.where $S_{c}$ is the net magnetization of the conduction electrons,expressed in units of Bohr magnetos per atom. The $\beta$ is positive and it is in the order of magnitude of electron volt.

The tird spin coupling arises from the fermi kinetic energy of the conduction band. Since the increase in the fermi kinetic energy is related to an unbalanced disturbution of conduction electrons,it must be an an even function of $S_{c}$ so we can represent this increase in energy by${\frac {1}{2}}\gamma s_{c}^{2}$per atom. $\gamma$can be represented in terms of the kinetic energy at the top of teh band and the number of electrons per atom. $\gamma ={\frac {2\epsilon }{3n}}$ so the total spin energy can be written in the following form:

$E_{spin}={\frac {1}{2}}\alpha s_{d}^{2}+\beta s_{d}s_{c}+{\frac {1}{2}}\gamma s_{c}^{2}$

since the contribution of conduction electrons is negligible, we can get the equiblirium value for $S_{c}$ when minimize energy

$S_{c}={\frac {\beta }{\gamma }}S_{d}$ by subtituation of the value of $S_{c}$ we can get:

$E_{spin}={\frac {1}{2}}{(\alpha -(\beta ^{2}/\gamma )})S_{d}^{2}$

the coefficient of $\alpha -(\beta ^{2}/\gamma )$ corresponds to the inner field of weiss.Thus, the type of the magnetic behavior is determined by the relative magnetitude of $\beta ^{2}$and$\alpha \gamma$

For ferromagnetism $\beta ^{2}>\alpha \gamma$

For antiferromagnetism$\beta ^{2}<\alpha \gamma$

although this peper does not develop the quantitative theory of ferromagnetism, it is enough to notice that the order of ferromagnetic coupling term. according to this theory it is in the order of magnitude of a teth of an ev per atom while the observed magnetization is not in this order.The power of this theory is in predicting the magnetic behavior of systems qualitatively. Ferromagnetism will be observed in all systemsfor which the first equation is satisfied. In these systems nighboring incomplete d shells are sufficiently far apart so the indirect intraction via the conduction electrons dominates over the direct antiferromagnetic coupling. The large distance of separation between incomplete d shells insures the ferromagnetism only when condunction electrons providethe necessary ferromagnetic coupling.

Why the Zener model is equivalent to RKKY interaction

The basic idea behind the RKKY interaction is based on the exchange coupling between the magnetic ion and the conduction band electrons. It should be mentioned that s and d wave functions are orthogonal and would not lead to any interaction in perfect one electron system. The conduction electron is magnetized in the vicinity of the magnetic ion, with the polarization decaying with distance from the magnetic ion in an oscillatory fashion(Friedel oscillation). This oscillation causes an indirect super-exchange interaction (RKKY)between two magnetic ions on the nearest or next near- est magnetic neighbors. This coupling may result ina parallel (ferromagnetic) or an anti-parallel (antiferromagnetic) setting of the moments dependent on these paration of the interacting atoms.

Dietl et al [reference]have shown that double exchange cannot lead to carrier induced ferro-magnetism for carrier densities lower than metals in Mn based III-V DMSs,and proposed the zener Model based on ferromagnetic interaction mediated by free carriers in tetrahedrally coordinated semiconductors. In the Zener model since the Mn d shell is half filled, the direct interaction between d shells of the adjacent Mn atoms lead to an antiferromagnetic configuration of d sell spins.On the other hand, the indirect coupling of spins through the conduction band tends to align the spin of the incomplete d shells in a ferromagnetic manner.

However, this model was later abandoned, as neither the itinerant character of the magnetic electrons nor the quantum (Friedel) oscillations of the electron spin polarization around the localized spins were taken into account; both of these are now established to be critical ingredients for the theory of magnetic metals. We emphasize that in the case of semiconductors, however, the effect of the Friedel oscillations averages to zero because the mean distance between the carriers is greater than that between the spins. Under such conditions, the exchange interaction mediated by the carriers is ferromagnetic for most of the spin pairs, which reduces the tendency toward spin-glass freezing. In fact, for a random distribution of the localized spins, the mean-field value of the Curie temperature T C deduced from the Zener model is equal to that obtained from the Ruderman, Kittel, Kasuya, and Yosida ͑RKKY͒ approach, in which the presence of the Friedel oscillations is explicitly taken into account. So Zener model becomes equivaent (13) to the approach developed by Ruderman, Kittel, Kasuya, and Yosida (RKKY), in which the presence of the oscillations is taken explicitly into account.

Mean field zener model

We can apply the zener Model of carrier-controlled ferromagnetism by introducing the functional of free energy $F[M(r)]$ . selecting the$M(r)$ as an order parameter means that the spins are treated as classical vectors. The starting point of the model is to determine how the Ginzburg-Landau free-energy functional F depends on the magnetization M of the localized spins. The hole con- tribution to F, $F_{c}[M(r)]$ , is computed by diagonalizing the $6\times 6$Kohn-Luttinger matrix together with the p-d exchange contribution