Superfluidity of neutron stars

Superfluidity

A superfluid is a very interesting substance. This substance has one particular quality which makes it special, it is a liquid with no viscosity. There are reasons for this. When poured through a tube, a viscous fluid will have no flow near the tube walls. As the tube's radius shrinks and the region of no flow fills the tube, a viscous fluid will eventually not flow. The absence of viscosity allows the fluid to flow freely! Not only does the fluid flow but it can flow up its containers walls. This can be seen in the following video which was shown in class.

{{#ev:youtube| 2Z6UJbwxBZI}}

The macroscopic properties of these substances are a result of two simple quantum conditions; the particles making up the substance must be bosons and the particles must all be in the lowest energy state. These conditions are achieved in simple ways. The first is that the particles must have an intrinsic integer spin, a requisite for being a boson. Most matter particles, such as protons, neutrons, and electrons, are all fermions having only half integer spins. This is resolved by pairing the particles, adding the two half integer spins making an integer spin. The second condition occurs for very low temperatures. Given sufficiently low temperatures (2.7 K for helium-4) none of the particles will be in an excited state. Given these two conditions the bosons, as a macroscopic object, will behave as a superfluid.

What Are Neutron Stars?

Stellar Evolution

A flow chart describing the many phases of stellar evolution.

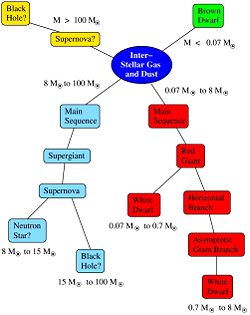
Neutron stars are one of the many possible ends to the life of a star. All stars begin as space dust, usually in a giant cloud. Should perturbations in the density of such a cloud permit sufficient mass to be within a certain radius, the cloud will collapse. These perturbations could include supernovae shock waves entering the dust cloud or objects like meteoroids entering the dust cloud. As the dust free-falls it will form a disk, most of which will eventually comprise the raw material of the star while the rest will form planets, moons, asteroids, and meteoroids. Assuming that the dust cloud is massive enough, the core of the condensed cloud will ignite forming a main sequence star. From this point on the star will undergo a series of burning stages where elements will fuse or "burn" in the core of the star. Once the fuel has run out in the core the burning stage will continue in an envelope around the core until the core shrinks enough for the temperature there reaches the limit for the next burning stage. This phase of stellar life is characterized by hydrogen burning via the pp-chain or CNO-cycle. Some stars (those of less than 0.7 solar masses) finish their lives here as the core contraction after the red giant phase cannot raise the temperature high enough to burn helium. These very low mass stars will become white dwarfs. Stars with greater mass will begin helium burning in the phase known as the horizontal branch. But even after helium shell burning, any star less than 8 solar masses will still turn into a white dwarf as the core will not become hot enough to produce carbon. Stars that are greater than eight solar masses will then begin burning helium to carbon and oxygen, carbon to neon, neon and oxygen to silicon, and silicon to nickel (nickel will then beta decay to cobalt and cobalt then decays to iron). Once the star produces nickel it is doomed as it cannot gain any more energy by fusing elements together. Of course mass limits the exact ending stage, but whatever the cause, when the burning does cease these stars explode.

The end state of any star occurs suddenly. Stars maintain a balance between the inward gravitational pressure and the outward energy pressure. But the star eventually cannot burn past a certain stage. The core of the star shrinks rapidly rapidly squeezing the atoms closer and closer together as each atom’s electron cloud battles to keep them apart. The outward pressure of this state, which characterizes the white dwarf, is known as the electron degeneracy pressure. With larger mass stars, the core shrinks so rapidly that there is too much pressure making it energetically favorable for the protons and electrons to react to form neutrons. The reverberation from this rapid compression is the classical cause of the supernova explosion. The neutrons then become degenerate and the star becomes a neutron star. If the mass then shrinks below the Schwarzschild radius, the star becomes a black hole. The Schwarzschild radius is given by:

$r_{s}=(3M/M_{\odot })km$

where M is the mass of the star and the M with the dot is the mass of the sun. Interestingly, after the red supergiant phase (after helium burning has ceased) the time it takes for the energy from the core to make it to the surface is 10,000 years. However, the rest of the star's life will last less than 1000 years. This means that the surface of the star has no idea that the star is dead until it explodes.

There is another method of neutron star formation. This method occurs only in binary star systems. After one of the two stars has become a white dwarf it may strip mass from its partner. After the white dwarf has stolen enough mass to reach the Chandrasekhar limit of 1.4 solar masses the white dwarf explodes leaving behind a neutron star (or black hole if the accretion is fast enough). This limit defines the mass at which the electron degeneracy pressure cannot hold up the mass of the star.

Properties of the Neutron Star

Composition

Neutron stars are composed of more than just neutrons. In fact should one stand on the surface the neutron star, one might actually be standing on a metal surface. This surface is composed of metals like iron, cobalt, and nickel in either a solid lattice (like an iron ball) or in a fluid form (like the entire star is one giant ocean). Also in the crust are degenerate electrons as seen in white dwarf stars. Below this "outer crust" is a very different inner crust. Here the star is composed of a lattice heavier nuclei like krypton, a superfluid of free neutrons, and more degenerate electrons. The interior of the neutron star is believed to consist of mostly a superfluid of free neutrons, but there are also superconducting protons and electrons. A debate still exists over whether the neutron star has a core consisting of smaller particles like pions.

Magnetism

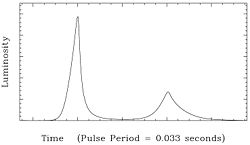
One of the most distinct features of a neutron star is its huge magnetic field and its fast rotation. These features produce a strong signal that appears to pulse as the star rotates. When discovered, these pulses mistakenly were thought first to be aliens then later pulses from a quasar. But after careful elimination the only viable cause of the pulses could be neutron stars. For this reason neutron stars are also known as pulsars. These pulses occur because the neutron star acts like a lighthouse where two beams (one for each magnetic pole) shoot out along the magnetic axis and the star itself spins. Then as beams sweep past earth, radio telescopes see pulses.

But where do these fields come from? The core of the progenitor star is made of iron and nickel. This core spins like the iron core of the Earth, only on a much grander scale. Like in the Earth, the rotation of the core causes magnetic fields to be produced. Two major effects occur to create the strong pulses seen in neutron stars. The first is that the star is essentially the same as the core of the progenitor, iron and nickel. The flux of the magnetic field through the surface of the star will be conserved as the star shrinks. So the as the radius decreases the magnetic field produced must increase! This is seen in the very simple derivation below.

$\Phi =\int BdA\;$

$BdA=B4\pi R^{2}\;$

And since the flux is conserved.

$\Delta \Phi =0\;$

$4\pi B_{i}R_{i}^{2}=4\pi B_{f}R_{f}^{2}$

$B_{f}=B_{i}({\frac {R_{i}}{R_{f}}})^{2}$

Just shrinking the earth to the size of a neutron star is a radius change of two orders of magnitude. This means that the magnetic field of the earth will need to increase by four orders of magnitude!

The second cause is the rapid rotation of the star which is due to the conservation of angular momentum. Stars rotate and orbit like planets. These rotations may be slow for the original core but considering the size difference after the collapse, the neutron star spins very rapidly. The change in rotational period has the same form as the change in magnetic field.

$P_{f}=P_{i}({\frac {R_{i}}{R_{f}}})^{2}$

The result of this can be seen in the pictures to the right.

Neutron stars have no form of energy generation and the high amount of spin and its magnetic fields require energy. So naturally this process will decay over a long period of time. However, the neutron star occasionally speeds up in its rotation. This event is known as a glitch. This phenomena is believed to be caused by vortices in the superfluid of the star.

A graph of the luminosity of the Crab Pulsar.

Actual image of the "pulsing" star in the Crab Nebula

Extreme Densities

As mentioned before, a star with eight times the mass of the sun is eligible to be a neutron star. The neutron star itself will not retain this mass as much of it will be blown away in the explosion. A white dwarf (which the sun will one day be) is usually about one hundredth the size of the sun, or about the size of the earth. Neutron stars are obviously much smaller than this. One can use a simple calculation to approximate the size of this star. From statistical physics one has the following relations for a gas:

The particle density: $n=\int _{0}^{\infty }{\omega (E)f(E)dE}\;$

The pressure: $P={1 \over 3}\int _{0}^{\infty }{pv\omega (E)f(E)dE}\;$

where omega is the state density, f is the probability distribution, p is the momentum, and v is the velocity. These values for a non-relativistic degenerate Fermi gas are:

$\omega (E)=4\pi {\frac {(2m)^{3/2}}{h^{3}}}E^{1/2}\;$

$f(E)={\frac {1}{e^{\frac {E-\mu }{k_{B}T}}+1}}\;$

$p={\sqrt {2mE}}\;$

$v={\sqrt {\frac {2E}{m}}}\;$

Then plugging these in to the equations for n and P.

$n=4\pi {\frac {(2m)^{3/2}}{h^{3}}}\int _{0}^{\infty }{{\frac {E^{1/2}}{e^{\frac {E-\mu }{k_{B}T}}+1}}dE}\;$

$P={\frac {8\pi }{3}}{\frac {(2m)^{3/2}}{h^{3}}}\int _{0}^{\infty }{{\frac {E^{3/2}}{e^{\frac {E-\mu }{k_{B}T}}+1}}dE}\;$

Then one can let $x={\frac {E}{k_{B}T}}\;$ one gets:

$n=4\pi {\frac {(2mk_{B}T)^{3/2}}{h^{3}}}\int _{0}^{\infty }{{\frac {x^{1/2}}{e^{x-{\frac {\mu }{k_{B}T}}}+1}}dx}\;$

$P={\frac {8\pi }{3}}{\frac {(2m)^{3/2}(k_{B}T)^{5/2}}{h^{3}}}\int _{0}^{\infty }{{\frac {x^{3/2}}{e^{x-{\frac {\mu }{k_{B}T}}}+1}}dx}\;$

These integrals are known as Fermi integrals which can be looked up in tables. But the general form is:

$F_{n}(\alpha )=\int _{0}^{\infty }{{\frac {x^{n}}{e^{x+\alpha }+1}}dx}\;$

Therefore the two integrals become:

$n=4\pi {\frac {(2mk_{B}T)^{3/2}}{h^{3}}}F_{1/2}({\frac {-\mu }{k_{B}T}})\;$

$P={\frac {8\pi }{3}}{\frac {(2m)^{3/2}(k_{B}T)^{5/2}}{h^{3}}}F_{3/2}({\frac {-\mu }{k_{B}T}})\;$

Then one can substitute n into P and get:

$P={\frac {2}{3}}nk_{B}T{\frac {F_{3/2}({\frac {-\mu }{k_{B}T}})}{F_{1/2}({\frac {-\mu }{k_{B}T}})}}\;$

Now one can take the limit as the argument of the Fermi function goes to negative infinity to represent the extreme degeneracy and get:

$\lim _{{\frac {-\mu }{k_{B}T}}\to -\infty }F_{3/2}({\frac {-\mu }{k_{B}T}})={\frac {2}{5}}({\frac {\mu }{k_{B}T}})^{5/2}$

$\lim _{{\frac {-\mu }{k_{B}T}}\to -\infty }F_{1/2}({\frac {-\mu }{k_{B}T}})={\frac {2}{3}}({\frac {\mu }{k_{B}T}})^{3/2}$

Which makes n and P:

$n=4\pi {\frac {(2mk_{B}T)^{3/2}}{h^{3}}}({\frac {2}{3}}({\frac {\mu }{k_{B}T}})^{3/2})\;$

$P={\frac {2}{3}}nk_{B}T({\frac {3}{5}}{\frac {\mu }{k_{B}T}})\;$

Then solving for $\mu /(k_{B}T)$ in the n equation and substituting into P:

${\frac {\mu }{k_{B}T}}=({\frac {3}{8\pi }}n)^{2/3}{\frac {h^{2}}{2mk_{B}T}}\;$

$P={\frac {h^{2}}{20m}}({\frac {3}{\pi }})^{2/3}n^{5/3}\;$

This is the equation for the pressure of an extremely degenerate Fermi gas. Pairing this with the equation for Hydrostatic Equilibrium one can get the radius of the star. The Hydrostatic Equilibrium equation is:

${\frac {\partial P}{\partial R}}=-{\frac {GM\rho }{R^{2}}}\;$

Here G is the gravitational constant, M is the mass of the star, and rho is the mass density. Integrating with the assumption of constant mass and density one gets:

$P={\frac {GM\rho }{R}}$

Now one needs to equate the two and solve. However to make this a little easier one can do the following to the density variables n and rho.

$n={\frac {\rho }{m_{N}}}\;$

$\rho ={\frac {3M}{4\pi R^{3}}}$

Though this may seem strange, this changes the density of particles to the mass density. Then makes the assumption of uniform density. Then solving one gets:

$R={\frac {h^{2}}{20}}({\frac {9}{4\pi ^{2}}})^{2/3}({\frac {1}{m_{N}}})^{8/3}{\frac {1}{GM^{1/3}}}$

From here one can input numbers. So a 1.4 solar mass neutron star will have a radius of about 4400 km. The calculation however is a good approximation of the order of magnitude of the true result which is about 12 km. From this one can see that something more massive than the sun can be reduced to the size of Tallahassee if it became a neutron star. As another order of magnitude result, the mass density of the star would be on the order of 4E14 g/cm^3. So one teaspoon of this would weigh roughly 4.5E12 lbs. Of course these calculations are crude but give a general idea of the order of magnitude of how dense this stellar body is and how powerful the neutron degeneracy pressure is to keep this body from crushing itself.

Superfluidity of Neutron Stars

In the earlier discussions of properties of neutron stars one sees that these stellar bodies exhibit extreme behaviors. Usually superfluids form at very low temperatures, but neutron stars are very hot. The simple explanation for superfluidity in a hot neutron star is the extreme pressure placed on the particles. Already in the formation of the neutron star the particles went from a gas in a balloon (normal state) to a bucket of golf balls (degenerate state). With even greater pressure it is favorable for the electrons to react with the protons to form neutrons in order to free the atoms from Coulomb repulsion. The density found in neutron stars is so high that these newly made neutrons are squeezed out of the atoms. It is very reasonable that these neutrons will pair up to further reduce the energy of the system. Once paired the two fermions will be a boson. The paired neutrons will also be crowded through pressure into the lowest energy state. The two major criteria of a superfluid have now been met: (a) the is a group of bosons and (b) the bosons are all in the lowest energy state.

References

All pictures are provided by Dr. Peter Hoeflich.