Unconventional superconductivity in nearly-magnetic metals
Superconductivity
The discovery of superconductivity was one of the most important discoveries of the 20th century with promises of many applications in every day life. A superconductor is a material in which electricity flows with no resistance. It was discovered by H.K. Onnes in 1911 after experimenting with the resistance of mercury at low temperatures. He discovered that the resistance sharply dropped to zero below the critical temperature (Tc) of ~4.2 K. Since then researches have been pushing the boundaries of the critical temperature in an attempt to make superconductors viable for practical uses by understanding and engineering materials that superconduct.
The core behind any superconductor is the so-called Cooper pair. These pairs consist of two electrons with opposite momentum and spin. A Cooper pair carries electricity like a normal charge carrier, but suffers from no scattering and zero resistance. Since the spins add, they are considered bosons and obey such statistics. These electrons have a lower energy than a normal electron, measured by the energy gap (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta E} ). An energy of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \Delta E} is required to break up a Cooper pair. Thus the frequency on the onset of absorption is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle hv = 2\Delta E}
Conventional Superconductivity
In most conventional superconductors, Cooper pairs form as a result of lattice interactions. These quantized phonon waves change the shape of the lattice, distorting it around an electron and creating a net positive charge. This attracts a second electron nearby, forming a Cooper pair. If the energy of this bound state is greater than the energy of the oscillations of atoms from heat, then the electron pair will remain bound. These new particles are bosons and can be described as a large Bose-Einstein condensate.
The interaction that provides the attraction between the paired electrons can be considered as a virtual phonon. This phonon is virtual because the electron cannot change its energy sufficiently (~ Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega_D} ) at temperatures below the Debye temperatures to create a real phonon of short wavelength. The timescale of the phonon is so small (< Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/\omega_D} ) that the existence is permitted by the energy-time uncertainty relation. Energy is conserved overall in the process. The BCS theory calculated many of the properties of superconductors by replacing the real interaction with this virtual instantaneous interaction spread out to a range ~Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_F/\omega_D} to allow for the distance moved by an electron during this characteristic time (1/Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_D} ) of ionic motion.
Magnetism in Superconductors
A superconductor's behavior in a magnetic field leads to the classification of Type I superconductors and Type II superconductors. All pure samples of superconducting elements are Type I superconductors, except Nb. This class of superconductors is characterized by the superconductivity being destroyed by applying a modest applied field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_c} , called the critical field. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_c} as a function of temperature is approximately shown as follows,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_c(T)=B_c(0)[1-(T/T_c)]}
For fields below the critical temperature, flux lines are expelled from the superconducting material. This is known as the Meissner effect, and is caused by electric currents, called "screening" currents, that are generated on the surface of the superconductor in such a way to create a field equal and opposite of the applied field. We can regard the superconductor as a magnetic material and the screening currents can be replaced by an equivalent magnetization, hence:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{B} = \mu_o (\mathbf{H}+\mathbf{M} )}
Which leads to,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{M} = -\mathbf{H}}
We can then say that a superconductor has a magnetic susceptibility of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi=-1} . Thus, a type I superconductor is often called a perfect diamagnet.
Type II superconductors become type II when the electron mean free path is reduced significantly by alloying the material. These superconductors also expel flux lines at a critical field, but this critical point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_c1} is lower than the critical field normally. Above Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_c1} there is partial flux penetration into the alloy, although it retains superconducting properties. The phase transition to the normal state where flux penetrates the entire object happens at a much higher field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_c2} .
The electrodynamics of the screening currents was first worked out by Fritz and Heinz London. They suggested that the currents are described by,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigtriangledown \times \mathbf{j}=-(n_S e^2/m)\mathbf{B}}
This is known as the London equation. They arrived there by taking the curl of this,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{j}=-(n_S e^2/m)\mathbf{A}}
By combining Maxwell's equations,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigtriangledown \times \mathbf{B}=\mu_o\mathbf{j}}
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigtriangledown \cdot \mathbf{B}=0}
We get the result for the field B inside a superconductor,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda ^2\bigtriangledown ^2\mathbf{B}=\mathbf{B}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda^2=m/\mu_o n_S e^2}
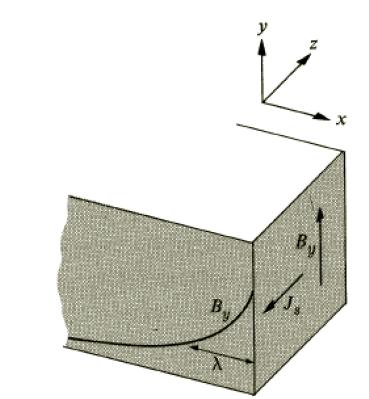
The magnetic field in the superconductor is of the form B = B(x)z when the field is parallel to the boundary in a vacuum. B(x) satifies
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda ^2\frac{\partial^2 }{\partial x^2}B=B}
The solution of this equation is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(x)=ae^{-x/\lambda}+be^{x/\lambda}}
The second term can be rejected, as it described a field increasing exponentially at large distances from the boundary and does not physically describe the system. We require Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = B_e} to satisfy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B = B_e} at x = 0. Therefore,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(x)=B_ee^{-x/\lambda}}
The characteristic length scale Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} is known as the penetration depth.
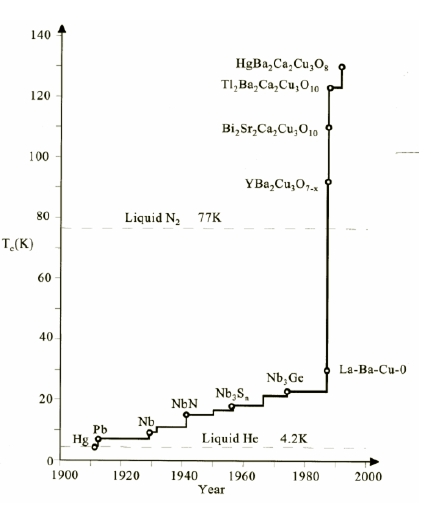
High-Temperature Superconductors
Before 1980 most physicists thought that there was a hard upper limit on the critical temperature of superconductors around 30 K. Many justified this with theoretical derivations. But in 1985 a new class of superconductors was found. These High-Tc Superconductors had a critical temperature reaching up to 164 K. These superconductors are all oxides. Most of these superconductors are ceramic and in the normal state do not conduct electricity very well except in one preferred direction. This has led physicists to believe that conduction is predominantly due to motion of carries in the oxide planes. By changing the location and number of oxygen atoms in the lattice, researchers have been able to discover the properties of these oxide superconductors. While some interpret the data as Cooper pairings with holes, flux quantum measurements that the pairings involve particles of charge e. The interaction responsible for these pairings is still unknown, but headway is being made on this unconventional superconductivity. It is important to discover the exact method of pairing in these oxide superconductors, as most real world applications require higher and higher critical temperatures in order to put these superconductors to use.
Unconventional Superconductors in Heavy Fermion Compounds
Although the exact method of pairing is not known in these high-Tc superconductors, many researchers are now arguing that magnetic spin-spin interactions are the cause. Heavy fermion compounds are the subject of some of these studies. The quasiparticles that form obey the fermion quantum statistics, yet can behave as 'heavy' particles. When these quasiparticles move throughout the substance, they create waves that affect other quasiparticles throughout the medium. The waves of interest occur when the lattice density reaches the critical density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_C} , which renders the system close to a state of continuous long range magnetic order. The waves in the non-magnetically ordered state are dampened, with a relaxation frequency of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_q} .
The dampened interaction depends on the product of three factors: the relative orientation and magnitude of the magnetic moments involved, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\mathbf{\mu_1}\cdot \mathbf{\mu_2}} , the square of the coupling parameter, and the space and time-dependent magnetic susceptibility, which depends on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_q} . Near the critical lattice density, magnetic waves propagate over long range. If the coupling parameter remains infinite, then the magnetic interactions will also be long range. This can lead to properties different from those in a normal metal. Also, for some orientations of the magnetic moments in certain regimes of space and time, this interaction can be attractive. Therefore at low enough temperatures, bound states can arise which can lead to superconductivity. In contract with conventional superconductors, the bound states have orbital and spin angular momentum. Magnetic interactions also tend to interfere with phonon interactions, thus suppressing conventional superconductivity in these nearly magnetic materials.
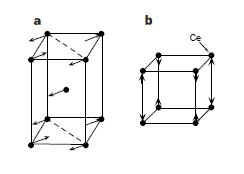
In choosing suitable materials, researchers include candidates in which the critical density can be reached with the available pressures, the states are metallic on both sides of the critical density with a single magnetic transition near Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_C} , the magnetic transition is continuous at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_C} (otherwise the magnetic interaction would not be long range nor necessarily dormant), and pair-breaking effects, like impurities, can be made small. The researchers at Cambridge discovered that f series metals provide the best candidates, as impurities are small and metallic transitions are continuous. To further narrow the search, the magnetic interaction model can be applied to a critical temperature Tc required for superconductivity. The model provides the relation,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c\approx \Gamma \theta \phi e^{-(1+\lambda )/g\lambda }}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma} is the bandwidth of the spectrum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_g} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} represents the enhancement of the quasiparticle mass due to magnetic interactions which depends on a q-space average of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_g} , and g measures the relative strength of the interaction in the given pair state. The factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} depends on the form of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_g} and in part represents the damping due to incoherent inelastic scattering. The factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} represents damping due to scattering from impurities. This model predicts superconductivity is widespread in Cerium-based heavy fermion compounds, yet despite the extensive search for decades, superconductivity has only been found at ambient pressure in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle CeCu_2Si_2} , though researchers are confident that collapse of Tc upon reaching Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_C} can be described by the pair breaking effects of magnetic interactions. The researchers chose the materials Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle CePd_2Si_2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle CeIn_3} for study, with the shape of the lattices shown below, respectively.
The researchers found that the evidence speaks strongly in favor of the existence of magnetically mediated superconductive state. Though the 'magnetic glue' that binds together electrons into Cooper pairs is hard to prove, the possibility is not ruled out that the existence is widespread.