Midterm Solution

Problem 1

Describe the difference between a first order and a second order phase transition. Give examples of each type. (10 points)

When determining the type of phase transition you must look at the change in the physical quantities of the material. If the change is sudden, a discontinuity in the first derivative of the free energy, then you have a first order phase transition. Examples of this would be water going from a liquid state to a gaseous state. A second order phase transition is continuous in the first derivative of the free energy and displays discontinuity only in the second derivative. With this fact, second order phase transitions will experience spontaneous symmetry breaking. Examples of a second order phase transition includes ferromagnetism, antiferromagnetism, and superconductivity.

Problem 2

Give some examples of spontaneous symmetry breaking. How does it depend on the system size? Explain how it can happen, in apparent violation of the ergodicity hypothesis of Boltzmann. According to Boltzmann, what determines the probability of some microscopic configuration (10 points)

Examples of spontaneous symmetry breaking are the same as those in second order phase transitions ferromagnetism, antiferromagnetism, and superconductivity. In order to have spontaneous symmetry breaking you must have an infinitely large system. If we have a finite system, spontaneous symmetry breaking could not occur. An example of spontaneous symmetry breaking as previously stated would be ferromagnetism. If we have a finite number of spins in our system then you will not be able to find a phase transition to the ferromagnetic state. With an infinite number of spins you will be in the thermodynamic limit and a ferromagnetic state will be able to be found. Boltzmann's ergodicity hypothesis states, in equilibrium each possible state of the system has the same energy and the same probability of existing. This means each possible state is equally populated. Viewing this hypothesis the system would transition over time visiting each possible state. The system does not necessarily violate the ergodicity hypothesis. The problem is the transition to each possible state can sometimes take much longer than our lifetimes or maybe even longer than the existence of the universe. We can determine this time as it is proportional to the probability. Looking at the probability of a microscopic configuration we get:

$P\thicksim e^{\sigma *L^{2}/T}$

Realistically these systems will not be microscopic, which will increase the L. It can then be seen why the system will take so long to transition as it increase exponentially with the system size.

Problem 3

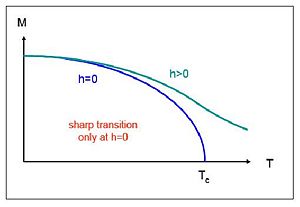
What determines the Curie temperature of a ferromagnet? How does it depend on the coordination number of the corresponding crystal lattice? Sketch the magnetization as a function of temperature in zero and in finite magnetic field. How does the field affect the transition? (10 points)

Their are two main components which determine the Curie Temperature of a ferromagnet. One is the coordination number of the material and the other is the magnetic exchange interaction. Given by the mean field theory, these two elements are proportional to each other when determining the Curie temperature. In our case the coordination number is the number of neighbors each magnetic spin has. The coordination number is determined by the type of crystal lattice. The higher the coordination number for each magnetic spin the more neighbors it has that can influence its spin direction. The magnetic exchange interaction is when two identical particles wave functions overlap and cause the spin expectation of each to change up or down.

The graph with an external magnetic field is sketched out in green and the graph without an external magnetic field is sketched in blue

Without external magnetic field

When looking at the graph of a present external magnetic field we can see the Curie Temperature is never reached, which is certainly a difference from the situation with an absent external magnetic field. Instead the graph will become asymptotic to zero.

Problem 4

The mean-field equation of state for a ferromagnet is given by the expression

$m=\tanh \left(\beta Jzm+\beta h\right)$.

Consider the system at high temperature, where nonzero magnetization is found only in presence of an external magnetic field. Assume that both the field and the magnetization are small, and determine (linearizing the RHS in m and h) the magnetization as a function of temperature, in presence of a weak field. Calculate the magnetic susceptibility and sketch its inverse as a function of T. Where does it diverge? (30 points)

The first step we need to take is to linearize the RHS of the equation. We can do this by considering only the first term of the taylor series expansion. The expansion of tanh(x) is the following:

Taylor Expansion of Failed to parse (syntax error): {\displaystyle {(\tanh x) = x-\frac{1}{3}x^3+\frac{2}{15}x^5} ==Problem 5== '''What is the physical principle behind the fact that atoms act as hard spheres, i.e. they have a “core” impenetrable to other atoms? (10 points) ''' Due to the Pauli Exclusion Principle all the core electrons of an atom cannot occupy the lowest energy state. Instead they must occupy different energy states. As a result this does not allow neighboring atom's core electrons to penetrate. This creates an impenetrable core and is the reason why we can have solid structures. ==Problem 6== '''Consider a molecule consisting of two identical atoms. Assume that the ground state energy of each atom is <math>E_o} , and that the corresponding hopping element between the two atoms is $t(R)$. Calculate the energy difference between the bonding and the anti-bonding molecular state for this molecule. How do you expect it to depend on the inter-atomic distance R? What is the energy needed to break the molecule, i.e. the energy of the covalent bond that binds the atoms in the molecule? (30 points)