Solution to Set 3

Ferromagnetism

Group 3 is the best

Ferromagnetism Ferromagnetic ordering of microscopic magnets (the magnetic moments of individual particles) Books Topics Magnetic Order Ferromagnetism Weiss field Solid State Physics Section 8.3 Section 8.4 Soft Condensed Matter Section 3.2

Given Information

• Classical Ising antiferromagnet on a ”bipartite” lattice given by Hamiltonian Failed to parse (syntax error): {\displaystyle H = \frac{J}{2} \sum_{<ij>} S_i S_j -− h\sum_i S_i } ,

• Magnetization for Lattice A: $m_{A}=<S^{(A)}>$

• Magnetization for Lattice B: $m_{B}=<S^{(B)}>$

• Average magnetization: $m={\frac {1}{2}}(m_{A}+m_{B}),$

• "Staggered” magnetization: $m^{\dagger }={\frac {1}{2}}(m_{A}-m_{B}),$

(Note: It's the difference between the two sublattices)

• $m=1\;$ for perfect ferromagnetic order

• $m^{\dagger }=1$ for perfect antiferromagnetic order

Part 1

Use Weiss mean-field decoupling to replace one of the spins in the Hamiltonian by its thermal average. The Weiss field experienced by a given spin is then proportional to the sublattice magnetization on the other sublattice. Write down self-consistent equations for $m_{A}\;$ and $m_{B}\;$, and express them through the order parameters $m\;$ and $m^{\dagger }$.

Given the Hamiltonian for a classical Ising antiferromagnet on a ”bipartite” lattice:

Failed to parse (syntax error): {\displaystyle H = \frac{J}{2} \sum_{<ij>} S_i S_j -− h\sum_i S_i }

where

• $H$ = Hamiltonian, the total energy of the system
• $J$ = Interaction Energy where J < 0 because it’s anti-ferromagnetic
• $S$ = Spin with value of 1 or -1
• $h$ = Magnetic field energy from external sources that breaks the symmetry

The magnetization on each sublattice

Part 2

Assume that $h=0\;$, so that $m=0\;$, and solve the mean-field equations by expanding in $m^{\dagger }$. Determine the Neel (ordering) temperature, and calculate the order-parameter exponent.

The Néel Temperature

Chapter 8.4 of Solid State Physics

$T_{N}={\frac {C\lambda }{2}}$

where

• $T_{N}\;$ is Néel Temperature, the onset temperature for antiferromagnetism
• $C={\frac {N\mu _{0}g^{2}\mu _{b}^{2}}{k_{B}}}$ is Curie constant
• $\lambda ={\frac {4\sum _{j\neq i}\jmath _{ij}}{N\mu _{0}g^{2}\mu _{b}^{2}}}=-{\frac {4z\jmath }{N\mu _{0}g^{2}\mu _{b}^{2}}}$

Part 3

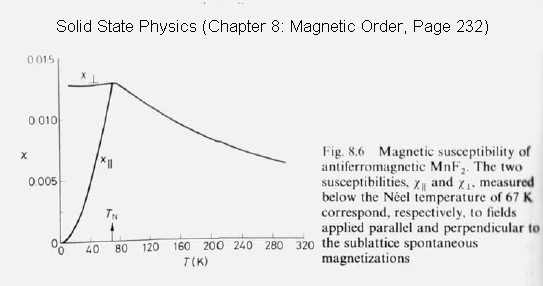
Now consider a small external field $h>0\;$, so that both order parameters can assume a nonzero value (Note: $m\;$ will be small). By keeping only the leading terms in $h\;$ and $m\;$, calculate the uniform spin susceptibility $\chi =\partial m/\partial h$, as a function of temperature. Plot $\chi \;$ as a function of temperature, and show that it has a cusp around $T_{N}\;$.

Part 4

Imagine adding a ”staggered” external field $h^{\dagger }$, which would be positive on sublattice A, but would be negative on sublattice B. Concentrate on the system with no uniform field $(h=0)\;$, and determine the behavior of the staggered susceptibility $\chi ^{\dagger }=\partial m^{\dagger }/\partial h^{\dagger }$. Show that $\chi ^{\dagger }$ blows up at the Neel temperature.