Geometrically Frustrated Materials

The main focus of solid state physics is on macroscopic properties of solid materials that result from interactions between atoms. Solid state physics is extremely interested in how these interaction come to an equilibrium to order in a certain way such as antiferromagnetism. One emergent property is disorder that arises from geometric frustration and this is the subject of much perplexing research because there seems to be no equilibrium between interactions or no unique ordering state.

What is geometric frustration?

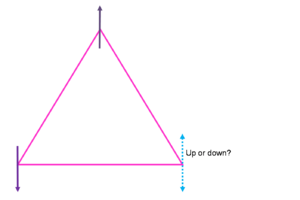
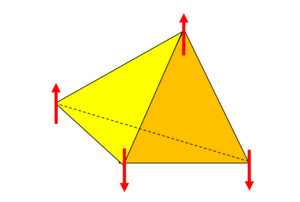
Frustration is the inability of a material to find a single ground state and instead has a highly degenerate ground state. The reason for this is because the geometry of the crystal is such that any arrangement of its constituent parts on the lattice cannot simultaneously satisfy all interactions. Most of the time this is referring to spins on a lattice in which the magnetic ordering is the subject of interest but this may also refer to the arrangement of oxygen and hydrogen atoms in water ice. In one dimension, consider a triangle with a spin on each vertex (see Fig.1). Two spins are satisfied and one spin is frustrated. That is, one spin can align up or down to satisfy a specific interaction but cannot satisfy all interactions. In three dimensions consider a tetrahedral where there is no possible configuration of four Ising spins on the vertices where they will all align antiferromagnetically (see Fig. 2). The size of the frustration parameter $f$, defined by the ratio of the Curie-Weiss temperature and the expected mean field ordering temperature (Néel or Curie temperature) or ${\frac {\theta _{CW}}{T_{N}}}$, is used to determine the extent of the frustration in a material. If $f<10$, then the material is said to be frustrated.

Figure 1. The configuration of spins on a triangle does not allow for all interaction to be satisfied. The left most spin can align up or down to compensate for its neighbor to the right or left but it cannot compensate for both spins at the same time

.

Figure 2. Four Ising spins on a tetrahedral lattice. Not all spins can align antiferromagnetically because they are arranged on the vertices of a tetehedra. The bottom right most spin interaction is satisfied but not the left most spin interaction.

.

The fact that these materials have degenerate ground states is important because this contributes to the strange properties that they exhibit. Instead of a ground state characterized by a single potential like in a ferromagnet, it is composed of many potential wells of various depths and this is thought to lead to properties like the randomly ordered spin freezing in a spin glass,

Water Ice

Water ice was the first geometrically frustrated material to be studied. In 1936 Giaugue and Stout published The Entropy of Water and the Third Law of Thermodynamics where they reported that water ice has a residual entropy of 185.3 J/(mol•K). To find this, they first measured the heat capacity of water from the liquid through the ice state in a calorimetry experiment. Then they integrated the results and added in the contributions from latent heat to find the entropy. The entropy in the limit of 0 K was found by extrapolating the low temperature values to 0 K.