PHY6937: Difference between revisions
| (280 intermediate revisions by 11 users not shown) | |||
| Line 15: | Line 15: | ||
To see the origins of superconductivity, it is helpful to look at a toy system, which we already know will give us superconducting behavior. This is useful because the toy system is only a simple change to a non-interacting electron gas. By adding in some small ''attractive'' interaction, we will arrive at a superconducting system! This interaction need only occur between two electrons occupying the same position in space (and necessarily having opposite spin!). Additionally, we still find the interesting behaviour regardless of the size of the interaction; the only requirement is that it be non-zero! | To see the origins of superconductivity, it is helpful to look at a toy system, which we already know will give us superconducting behavior. This is useful because the toy system is only a simple change to a non-interacting electron gas. By adding in some small ''attractive'' interaction, we will arrive at a superconducting system! This interaction need only occur between two electrons occupying the same position in space (and necessarily having opposite spin!). Additionally, we still find the interesting behaviour regardless of the size of the interaction; the only requirement is that it be non-zero! | ||
We can write the Hamiltonian of the system as: | Our toy model will be that of free fermions with an attractive contact interaction. We can write the Hamiltonian of the system as: | ||
<math>H=\sum_\vec{r}[\psi_\sigma^\dagger (\vec{r})(\epsilon_\vec{p}-\mu)\psi_\sigma^\dagger (\vec{r}) +g\psi_\uparrow^\dagger (\vec{r})\psi_\downarrow^\dagger (\vec{r})\psi_\downarrow (\vec{r})\psi_\uparrow (\vec{r})]</math> | <math>H=\sum_\vec{r}[\psi_\sigma^\dagger (\vec{r})(\epsilon_\vec{p}-\mu)\psi_\sigma^\dagger (\vec{r}) +g\psi_\uparrow^\dagger (\vec{r})\psi_\downarrow^\dagger (\vec{r})\psi_\downarrow (\vec{r})\psi_\uparrow (\vec{r})]</math> | ||
| Line 34: | Line 34: | ||
<math>\psi^\dagger</math> and <math>\ \psi</math> are grassmann numbers. | <math>\psi^\dagger</math> and <math>\ \psi</math> are grassmann numbers. | ||
<math>\ \Delta^*</math> and <math>\ \Delta</math> are | <math>\ \Delta^*</math> and <math>\ \Delta</math> are normally commuting variables. | ||
<math>\psi_\uparrow\psi_\downarrow</math> and <math>\psi_\downarrow\psi_\uparrow</math> behave like constant. | <math>\psi_\uparrow\psi_\downarrow</math> and <math>\psi_\downarrow\psi_\uparrow</math> behave like constant (paired fermions behaving like bosons). | ||
Let's make a shift of the | Let's make a shift of the new integration variables: | ||
<math>\Delta \rightarrow \Delta+g\psi_\uparrow\psi_\downarrow</math> | <math>\Delta \rightarrow \Delta+g\psi_\uparrow\psi_\downarrow</math> | ||
| Line 43: | Line 43: | ||
<math>\Delta^*\rightarrow \Delta^*+g\psi^\dagger_\downarrow\psi^\dagger_\uparrow</math> | <math>\Delta^*\rightarrow \Delta^*+g\psi^\dagger_\downarrow\psi^\dagger_\uparrow</math> | ||
Then, <math>S_\Delta=-\int_0^\beta d\tau \sum_{\vec{r}} | Then, <math>S_\Delta=-\int_0^\beta d\tau \sum_{\vec{r}}\left [\frac{1}{g}\Delta^*\Delta + \Delta^*\psi_\uparrow \psi_\downarrow + \Delta\psi^\dagger_\downarrow \psi^\dagger_\uparrow+g\psi^\dagger_\downarrow \psi^\dagger_\uparrow \psi_\uparrow \psi_\downarrow\right ]</math> | ||
<math>\begin{align}S=&S_{BCS}+S_{\Delta}\\ | <math>\begin{align}S=&S_{BCS}+S_{\Delta}\\ | ||
| Line 53: | Line 53: | ||
then, <math>Z=\int D[\psi_{\sigma}^{*}(\tau,\mathbf{r}),\psi_{\sigma}(\tau,\mathbf{r})]D[\Delta^{*}(\tau,\mathbf{r}),\Delta(\tau,\mathbf{r})]e^{-(S_{0}+S_{int.}+S_{\Delta})}</math>. | then, <math>Z=\int D[\psi_{\sigma}^{*}(\tau,\mathbf{r}),\psi_{\sigma}(\tau,\mathbf{r})]D[\Delta^{*}(\tau,\mathbf{r}),\Delta(\tau,\mathbf{r})]e^{-(S_{0}+S_{int.}+S_{\Delta})}</math>. | ||
<math>\left\langle e^{-S_{int.}}\right\rangle _{0}\cong exp[\frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}+\frac{1}{4!}(\left\langle S_{int.}^{4}\right\rangle _{0}-3\left\langle S_{int.}^{2}\right\rangle _{0}^{2})]</math> by cumulant expansion, which guarantees that until the 2nd order, it is accurate. | <math>\left\langle e^{-S_{int.}}\right\rangle _{0}\cong \exp\left [\frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}+\frac{1}{4!}\left (\left\langle S_{int.}^{4}\right\rangle _{0}-3\left\langle S_{int.}^{2}\right\rangle _{0}^{2}\right )\right ]</math> by cumulant expansion, which guarantees that until the 2nd order, it is accurate. | ||
Use Matsubara's Method | Use Matsubara's Method | ||
| Line 89: | Line 89: | ||
<math>\Rightarrow=-\frac{1}{L^{D}}\frac{1}{\beta}\underset{\mathbf{k}}{\sum}\frac{1}{\varepsilon_{\mathbf{q}-\mathbf{k}}+\varepsilon_{\mathbf{k}}-2\mu-i\Omega_{n}}[\frac{1}{e^{\beta(\varepsilon_{\mathbf{q}}-\mu)}+1}-\frac{1}{e^{\beta(-\varepsilon_{\mathbf{q}-\mathbf{k}}+\mu)}+1}]=\int\frac{d^{D}k}{(2\pi)^{D}}\frac{1}{\varepsilon_{\mathbf{q}}+\varepsilon_{\mathbf{q}-\mathbf{k}}-2\mu-i\Omega_{n}}[1-f(\varepsilon_{\mathbf{k}})-f(\varepsilon_{\mathbf{q}-\mathbf{k}})].</math> | <math>\Rightarrow=-\frac{1}{L^{D}}\frac{1}{\beta}\underset{\mathbf{k}}{\sum}\frac{1}{\varepsilon_{\mathbf{q}-\mathbf{k}}+\varepsilon_{\mathbf{k}}-2\mu-i\Omega_{n}}[\frac{1}{e^{\beta(\varepsilon_{\mathbf{q}}-\mu)}+1}-\frac{1}{e^{\beta(-\varepsilon_{\mathbf{q}-\mathbf{k}}+\mu)}+1}]=\int\frac{d^{D}k}{(2\pi)^{D}}\frac{1}{\varepsilon_{\mathbf{q}}+\varepsilon_{\mathbf{q}-\mathbf{k}}-2\mu-i\Omega_{n}}[1-f(\varepsilon_{\mathbf{k}})-f(\varepsilon_{\mathbf{q}-\mathbf{k}})].</math> | ||
In the static (<math>\ \Omega_{n}=0</math>) and uniform (<math>\mathbf{q}=0</math>) limit,<math> 1-2f(\varepsilon_{\mathbf{k}})= | In the static (<math>\ \Omega_{n}=0</math>) and uniform (<math>\mathbf{q}=0</math>) limit,<math> 1-2f(\varepsilon_{\mathbf{k}})=\tanh[\frac{\beta}{2}(\varepsilon_{\mathbf{k}}-\mu)]</math>. | ||
Then <math>\chi_{p}(0,0)=\int\frac{d^{D}k}{(2\pi)^{D}}\frac{ | Then <math>\chi_{p}(0,0)=\int\frac{d^{D}k}{(2\pi)^{D}}\frac{\tanh[\frac{\beta}{2}(\varepsilon_{\mathbf{k}}-\mu)]}{2(\varepsilon_{\mathbf{k}}-\mu)}</math>. | ||
In low energy, integrate the energy in the shell near Fermi energy: | In low energy, integrate the energy in the shell near Fermi energy: | ||
| Line 97: | Line 97: | ||
[[Image:Fig.3.jpg]] | [[Image:Fig.3.jpg]] | ||
<math>\Rightarrow\chi_{p}(0,0)\cong N(0)\int_{\hbar\omega_{D}}^{-\hbar\omega_{D}}d\xi\frac{ | <math>\Rightarrow\chi_{p}(0,0)\cong N(0)\int_{\hbar\omega_{D}}^{-\hbar\omega_{D}}d\xi\frac{\tanh[\xi\beta/2]}{2\xi}\cong N(0)\int_{0}^{-\hbar\omega_{D}}d\xi\frac{\tanh[\xi\beta/2]}{\xi}=N(0)\ln[\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T}].</math> | ||
Then <math>\frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}=L^{D}\frac{1}{\beta}\chi_{p}(0,0)\underset{\Omega_{n},\mathbf{q}}{\sum}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})</math>. | Then <math>\frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}=L^{D}\frac{1}{\beta}\chi_{p}(0,0)\underset{\Omega_{n},\mathbf{q}}{\sum}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})</math>. | ||
| Line 103: | Line 103: | ||
If we ignore the higher order in the cumulant expansion, | If we ignore the higher order in the cumulant expansion, | ||
<math>S_{eff}=-\underset{\mathbf{r}}{\sum}\int_{0}^{\beta}d\tau\frac{1}{g}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})-\frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}=\underset{\mathbf{r}}{\sum}\int_{0}^{\beta}d\tau[\frac{1}{\left|g\right|}-N(0)ln(\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T})]\Delta^{*}(\tau,\mathbf{r})\Delta(\tau,\mathbf{r})</math>. | <math>S_{eff}=-\underset{\mathbf{r}}{\sum}\int_{0}^{\beta}d\tau\frac{1}{g}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})-\frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}=\underset{\mathbf{r}}{\sum}\int_{0}^{\beta}d\tau[\frac{1}{\left|g\right|}-N(0)\ln(\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T})]\Delta^{*}(\tau,\mathbf{r})\Delta(\tau,\mathbf{r})</math>. | ||
Remember the partition function <math>Z=\int D\Delta^{*}D\Delta e^{-S_{eff}(\Delta)}</math>. To look at superconductivity, we really only must consider the <math>\Delta</math> related factors. | |||
The superconductivity phase transition temperature is the temperature makes | The superconductivity phase transition temperature is the temperature that makes | ||
<math>{\frac{1}{\left|g\right|}}-N(0){\ln(\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T})}=0</math>, | |||
which happens at | |||
<math>T_{c}=\frac{\hbar\omega_{D}}{k_{B}}\frac{2}{\pi}e^{\gamma}e^{-\frac{1}{N(0)\left|g\right|}}=1.134\frac{\hbar\omega_{D}}{k_{B}}e^{-\frac{1}{N(0)\left|g\right|}}</math>. | |||
Above this critical temperature, the coefficient of the <math>\Delta^*\Delta</math> term becomes positive, and it is energetically unfavorable to have cooper pairs, as in the normal state. Below the critical temperature, the <math>\Delta</math> related factors in the partition function will diverge, which means superconductivity phase transition. Notice that this happens for ''any value of'' <math>|g|</math>! No matter how small the attraction between our fermions is, we can still find this funny (as of yet, it has not been shown to be specifically superconducting!) behaviour. | |||
Finite <math>\vec{q}</math> (small) <math>\ (\Omega_n=0)</math> | Finite <math>\vec{q}</math> (small) <math>\ (\Omega_n=0)</math> | ||
| Line 149: | Line 155: | ||
\chi_p(q,0)-\chi_p(0,0) | \chi_p(q,0)-\chi_p(0,0) | ||
&=\frac{1}{\beta}\sum_{i\omega_n}N(0)\int\frac{d\Omega}{\Omega_D}(q\cdot v_F)^2\frac{2\pi i}{(2i|\omega|)^3}\\ | &=\frac{1}{\beta}\sum_{i\omega_n}N(0)\int\frac{d\Omega}{\Omega_D}(q\cdot v_F)^2\frac{2\pi i}{(2i|\omega|)^3}\\ | ||
&=N(0)v_F^2|\vec{q}|^2\int\frac{d\Omega}{\Omega_D}(q\cdot v_F)^2 \frac{1}{\beta}\sum_{i\omega}\frac{2\pi i}{- | &=N(0)v_F^2|\vec{q}|^2\int\frac{d\Omega}{\Omega_D}(q\cdot v_F)^2 \frac{1}{\beta}\sum_{i\omega}\frac{2\pi i}{-8i|\frac{(2n+1)\pi}{\beta}|^3}\\ | ||
&=-\frac{1}{4}N(0)v_F^2q^2(<(\hat{q}\cdot \hat{v_F})>_{F.S.})\frac{\beta^2}{\pi^2}(\sum_{N=-\infty}^{+\infty}\frac{1}{|2n+1|^3}) | &=-\frac{1}{4}N(0)v_F^2q^2(<(\hat{q}\cdot \hat{v_F})>_{F.S.})\frac{\beta^2}{\pi^2}(\sum_{N=-\infty}^{+\infty}\frac{1}{|2n+1|^3}) | ||
\end{align} | \end{align} | ||
| Line 167: | Line 173: | ||
<math> | <math> | ||
\int\frac{d\Omega}{\Omega_D}(\hat{q}\cdot\hat{v}_F)^2=\frac{2\pi}{4\pi}\int_{-1}^{1} | \int\frac{d\Omega}{\Omega_D}(\hat{q}\cdot\hat{v}_F)^2=\frac{2\pi}{4\pi}\int_{-1}^{1}d(\cos{\theta})\,\cos^2{\theta} = \frac{1}{3} | ||
</math> | </math> | ||
| Line 173: | Line 179: | ||
<math> | <math> | ||
\int\frac{d\Omega}{\Omega_D}(\hat{q}\cdot\hat{v}_F)^2=\frac{1}{2\pi}\int_{0}^{2\pi}d\theta cos^2\theta = \frac{1}{2} | \int\frac{d\Omega}{\Omega_D}(\hat{q}\cdot\hat{v}_F)^2=\frac{1}{2\pi}\int_{0}^{2\pi}d\theta\,\cos^2{\theta} = \frac{1}{2} | ||
</math> | </math> | ||
| Line 192: | Line 198: | ||
\begin{align} | \begin{align} | ||
\frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}&=L^{D}\frac{1}{\beta}\underset{\Omega_{n},\mathbf{q}}{\sum}\chi_{p}(q,0)\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n}) \\ | \frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}&=L^{D}\frac{1}{\beta}\underset{\Omega_{n},\mathbf{q}}{\sum}\chi_{p}(q,0)\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n}) \\ | ||
&=N(0)ln[\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T}]L^{D}\frac{1}{\beta}\underset{\Omega_{n},\mathbf{q}}{\sum}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})-L^{D}\frac{1}{\beta}\underset{\Omega_{n},\mathbf{q}}{\sum}N(0)q^{2}\xi^{2}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n}) | &=N(0)\ln[\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T}]L^{D}\frac{1}{\beta}\underset{\Omega_{n},\mathbf{q}}{\sum}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})-L^{D}\frac{1}{\beta}\underset{\Omega_{n},\mathbf{q}}{\sum}N(0)q^{2}\xi^{2}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n}) | ||
\end{align} | \end{align} | ||
</math>. | </math>. | ||
<math>S_{eff}=\underset{\mathbf{r}}{\sum}\int_{0}^{\beta}d\tau\left[\left(\frac{1}{\left|g\right|}-N(0)ln(\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T})\right)\Delta^{*}(\tau,\mathbf{r})\Delta(\tau,\mathbf{r})-N(0)\xi^{2}(\nabla\cdot\Delta^{*}(\tau,\mathbf{r}))(\nabla\cdot\Delta(\tau,\mathbf{r}))\right]</math>. | <math>S_{eff}=\underset{\mathbf{r}}{\sum}\int_{0}^{\beta}d\tau\left[\left(\frac{1}{\left|g\right|}-N(0)\ln(\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T})\right)\Delta^{*}(\tau,\mathbf{r})\Delta(\tau,\mathbf{r})-N(0)\xi^{2}(\nabla\cdot\Delta^{*}(\tau,\mathbf{r}))(\nabla\cdot\Delta(\tau,\mathbf{r}))\right]</math>. | ||
Note that the last term in the expression tells us that <math> S_{eff} </math> would increase if gradient of <math> \Delta </math> is not zero. | Note that the last term in the expression tells us that <math> S_{eff} </math> would increase if gradient of <math> \Delta </math> is not zero. | ||
| Line 211: | Line 217: | ||
[[Image:Layout48.gif]] | [[Image:Layout48.gif]] | ||
As shown in the above figure, a thin shell of superconductor with radius R is placed in a small uniform magnetic field passing through the hollow center of the cylinder. The experiment intends to show the variation of the critical temperature with change of the magnetic field passing through the hollow superconductor cylinder. This was [http://prl.aps.org/abstract/PRL/v9/i1/p9_1| done in 1962], by Little and Parks at Stanford University. | |||
Before showing | Before showing the mathematics behind the experiment, we first have to rewrite the Giznburg-Landau functional to take the presence of magnetic field into account. The Hamiltonian for a free electron moving in a magnetic field is written as: | ||
<math> \frac{1}{2m}(p+\frac{eA}{c})^{2}\psi + V\psi = E\psi </math> | <math> \frac{1}{2m}(p+\frac{eA}{c})^{2}\psi + V\psi = E\psi </math> | ||
The | The physically observable magnetic field <math>\vec{B}</math> would remain the same if we choose a different vector potential | ||
<math> A\rightarrow A+ \nabla \chi </math> ( | <math> A\rightarrow A+ \nabla \chi </math> (or perform a gauge transformation). To maintain the same eigen-energy E which is observable, the wave function has to undergo a phase change: | ||
<math> \psi \rightarrow e^{i\phi}\psi </math> where <math> \phi=\frac{e}{c\hbar}\chi </math> | <math> \psi \rightarrow e^{i\phi}\psi </math> where <math> \phi=\frac{e}{c\hbar}\chi </math> | ||
Now in our | Now in our effective action, the wave function appears as | ||
<math> \Delta^{*}(\tau,\vec{r})\psi_\uparrow (\tau,\vec{r})\psi_\downarrow (\tau,\vec{r}) + \Delta(\tau,\vec{r}) \psi_\downarrow^\dagger (\tau,\vec{r})\psi_\uparrow^\dagger (\tau,\vec{r}) </math> | <math> \Delta^{*}(\tau,\vec{r})\psi_\uparrow (\tau,\vec{r})\psi_\downarrow (\tau,\vec{r}) + \Delta(\tau,\vec{r}) \psi_\downarrow^\dagger (\tau,\vec{r})\psi_\uparrow^\dagger (\tau,\vec{r}) </math> | ||
since <math> \psi \rightarrow e^{i\phi}\psi </math>, | since <math> \psi \rightarrow e^{i\phi}\psi </math>, if we want the effective action to remind the same, <math>\ \Delta </math> has to transform as <math> \Delta \rightarrow e^{-2i\phi}\Delta </math> | ||
Since <math>\ \Delta </math> corresponds to <math>\ \Psi </math> in the Giznburg-Landau functional, so the Giznburg-Landau functional is modified as | Since <math>\ \Delta </math> corresponds to <math>\ \Psi </math> in the Giznburg-Landau functional, so the Giznburg-Landau functional is modified as | ||
| Line 230: | Line 237: | ||
<math> F=\int d^{D}r\left[ \alpha (T-T_{c}) |\Psi(\vec{r})|^{2}+\frac{1}{2m^{*}}| ( \frac{\hbar \nabla}{i} - \frac{2e}{c}A(\vec{r}) ) \Psi(\vec{r})|^{2} \right] </math> | <math> F=\int d^{D}r\left[ \alpha (T-T_{c}) |\Psi(\vec{r})|^{2}+\frac{1}{2m^{*}}| ( \frac{\hbar \nabla}{i} - \frac{2e}{c}A(\vec{r}) ) \Psi(\vec{r})|^{2} \right] </math> | ||
choose symmetric gauge: | Note that the last term looks like a particle of charge <math>-2e</math> in a magnetic field! | ||
Now, we choose the symmetric gauge: | |||
<math> \vec{A}=\frac{1}{2}\vec{H}\times\vec{r}=\frac{1}{2}Hr\hat{\phi} </math> | <math> \vec{A}=\frac{1}{2}\vec{H}\times\vec{r}=\frac{1}{2}Hr\hat{\phi} </math> | ||
Re-write in cylindrical coordinates: | |||
<math> \vec{\nabla}=\hat{r}\frac{\partial}{\partial r} + \frac{\hat{\phi}}{r}\frac{\partial}{\partial \phi} + \hat{z}\frac{\partial}{\partial z} </math> | |||
Define the unit flux as <math> \Phi_{0}=\frac{hc}{2e} </math> | |||
Define the fluxoid as <math> \Phi(R) = \pi HR^{2}\ </math>, so we have | |||
<math> \begin{align} F&=\int d^{D}r\left[ \alpha (T-T_{c})|\Psi(\vec{r})|^{2} | <math> \begin{align} F&=\int d^{D}r\left[ \alpha (T-T_{c})|\Psi(\vec{r})|^{2} | ||
| Line 247: | Line 259: | ||
When <math> \Phi = N\Phi_{0}\ </math>, the critical temperature will remain the same and the phase of <math> \Psi\ </math> is changed as <math> \Psi \rightarrow e^{iN\phi} \Psi </math>. When <math> \Phi \neq N\Phi_{0}\ </math>, the critical temperature is found to vary as | When <math> \Phi = N\Phi_{0}\ </math>, the critical temperature will remain the same and the phase of <math> \Psi\ </math> is changed as <math> \Psi \rightarrow e^{iN\phi} \Psi </math>. When <math> \Phi \neq N\Phi_{0}\ </math>, the critical temperature is found to vary as | ||
<math> T_{c}^{new}=T_{c}- \frac{\hbar^{2}}{2m^{*}R^{2}\alpha}\left (N-\frac{\Phi}{\Phi_{0}}\right )^{2}</math>. See the | <math> T_{c}^{new}=T_{c}- \frac{\hbar^{2}}{2m^{*}R^{2}\alpha}\left (N-\frac{\Phi}{\Phi_{0}}\right )^{2}</math>. See the figure below. | ||
[[Image:Graph49.gif]] | [[Image:Graph49.gif]] | ||
== Microscopic derivation of the | This experiment is significant evidence that the objects represented by <math>\Delta</math> carry a charge twice that of a single electron. As we know that this thing stands in the equations for a cooper pair, this makes perfect sense! | ||
== Microscopic derivation of the Ginzburg-Landau functional == | |||
Let us consider the model of a metal close to the transition to the superconducting state. A complete description of its thermodynamic properties can be done through the calculation of the partition function. | |||
=== Ginzburg-Landau Functional === | |||
The classical part of the Hamiltonian in the partition function, dependent of bosonic fields, may be chosen in the spirit of the Landauer theory of phase transition. However, in view of the space dependence of wave functions, Ginzberg and Landauer included in it additionally the first non vanishing term of the expansion over the gradient of the fluctuation field. Symmetry analysis shows that it should be quadratic. The weakness of the field coordinate dependence permits to omit the high-order terms of such an expansion. Therefore, the classical part of the Hamiltonian of a metal close to a superconducting transition related to the presence of the fluctuation Cooper pairs in it (the so called Ginzberg-Landauer functional)can be written as | |||
<math>F[\psi(r)]=F_{n}+\int dV\{a\mid\psi(r)\mid^{2}+\frac{b}{2}\mid\psi(r)\mid^{4}+\frac{1}{4m}\mid\nabla\psi(r)\mid^{2}\}</math> | |||
The basic postulate of G-L is that if <math>\psi</math> is small and varies slowly in space, so we can expand the free energy in a series of <math>\mid\psi(r)\mid^{2}</math>.These two terms should be adequate so long as one stays near the second-order phase transition at <math>T_{c}</math>, where the order parameter <math>\mid\psi(r)\mid^{2}\rightarrow0</math>. Inspection of G-L functional shows that <math>b</math> must be positive if the theory is to be useful; otherwise the lowest free energy would occur for arbitrarily large values of <math>\mid\psi(r)\mid^{2}</math>, where the expansion is surely inadequate. | |||
We already got the quadratic terms in the Ginzberg-Landauer by expanding <math><e^{-S_{int}}></math> to the second order, and we are going to go the higher order. As we discussed, we expect that this term will be a negative value to keep <math>S_{eff}</math> as a negative value under <math>T_{c}</math>. To catch this goal we start with the partition function: | |||
<math>Z=Z_{0}< e^{-S_{int}} ></math> | <math>Z=Z_{0}< e^{-S_{int}} ></math> | ||
| Line 258: | Line 285: | ||
<math>Z_{0}=\int D\psi ^{*} D\psi D\Delta ^{*} D\Delta e^{-(S_{\Delta} +S_{0})}</math> | <math>Z_{0}=\int D\psi ^{*} D\psi D\Delta ^{*} D\Delta e^{-(S_{\Delta} +S_{0})}</math> | ||
we can expand this average for small<math>\Delta</math> near<math>T_{c}</math>, for this perpose we can assume | we can expand this average for small <math>\Delta</math> near <math>T_{c}</math>, for this perpose we can assume a second order phase transition so that it increases continiously from zero to finite number after <math>T_{c}</math>. | ||
so that it increases continiously from zero to finite number after <math>T_{c}</math> | |||
we need to calculate the average of <math>e^{-s_{int}}</math>which can be calculated by Tylor expansion: | we need to calculate the average of <math>e^{-s_{int}}</math>which can be calculated by Tylor expansion: | ||
<math>e^{-S_{int}}=<-S_{int}+\frac{1}{2}S_{int}^{2}-\frac{1}{3}S_{int}^{3}+\frac{1}{4!}S_{int}^{4}+...> | <math>e^{-S_{int}}=<1-S_{int}+\frac{1}{2}S_{int}^{2}-\frac{1}{3}S_{int}^{3}+\frac{1}{4!}S_{int}^{4}+...></math> | ||
=<math>1-<S_{int}>+\frac{1}{2} < S_{int}^{2}> -\frac{1}{3!}< S_{int}^{3}> +\frac{1}{4!}< S_{int}^{4}> +...</math> | |||
<math> | In this expansion all odd power terms go to zero because when we calculate the integral over <math>\psi</math> and its complex conjugate it will vanish since we have odd numbers of <math>\psi</math> or <math>\psi^{*}</math> in the integral. Then, we try to approximate it to | ||
<math>e^{\frac{1}{2}< S_{int}^{2}>}e^{\frac{1}{4!}< S_{int}^{4}>-\lambda }</math> . | |||
if we expand these two terms in to the second order the following expression can be got: | if we expand these two terms in to the second order the following expression can be got: | ||
| Line 277: | Line 302: | ||
<math>=1+\frac{1}{2} < S_{int}^{2}>+\frac{1}{8}(< S_{int}^{2}>)^{2} +...)+\frac{1}{4!}< S_{int}^{4}>-\lambda +...</math> | <math>=1+\frac{1}{2} < S_{int}^{2}>+\frac{1}{8}(< S_{int}^{2}>)^{2} +...)+\frac{1}{4!}< S_{int}^{4}>-\lambda +...</math> | ||
<math>\lambda</math> can be | <math>\lambda</math> can be chose in a such way that this result will match to the original expansion of <math>e^{-s_{int}}</math> up to the forth power of <math>s_{int}</math> : | ||
so, | so, | ||
| Line 289: | Line 314: | ||
<math>S_{int}=\frac{L^{D}}{\beta ^{2}}\sum_{\omega _{n},\Omega _{n}}\sum _{k,q}[\Delta ^{*}_{q}(i\Omega _{n})\psi_{\downarrow}(i\Omega _{n}-i\omega _{n}),\vec{q}-\vec{k})\psi_{\uparrow}(i\omega _{n},k)+\Delta _{q}(i\Omega_{n})\psi_{\uparrow}^{\dagger }(i\omega _{n},k)\psi_{\downarrow}^{\dagger }(i\Omega _{n}-i\omega _{n}),\vec{q}-\vec{k})]</math> | <math>S_{int}=\frac{L^{D}}{\beta ^{2}}\sum_{\omega _{n},\Omega _{n}}\sum _{k,q}[\Delta ^{*}_{q}(i\Omega _{n})\psi_{\downarrow}(i\Omega _{n}-i\omega _{n}),\vec{q}-\vec{k})\psi_{\uparrow}(i\omega _{n},k)+\Delta _{q}(i\Omega_{n})\psi_{\uparrow}^{\dagger }(i\omega _{n},k)\psi_{\downarrow}^{\dagger }(i\Omega _{n}-i\omega _{n}),\vec{q}-\vec{k})]</math> | ||
let's write <math>S_{int}</math> in | let's write <math>S_{int}</math> in terms of <math>a</math> for simplification. where | ||
<math>a=\int \Delta ^{*}(1)\psi_{\downarrow}(1) \psi_{\uparrow}(1)+\Delta (1)\psi_{\downarrow}^{*}(1) \psi_{\uparrow}^{*}(1)</math> | <math>a=\int \Delta ^{*}(1)\psi_{\downarrow}(1) \psi_{\uparrow}(1)+\Delta (1)\psi_{\downarrow}^{*}(1) \psi_{\uparrow}^{*}(1)</math> | ||
<math>a_{1}</math> is a couple | <math>a_{1}</math> is a couple Grassman number, so we do not need to be worry about the sign when these terms commute with other terms. | ||
<math>< S_{int}^{4}> =\int_{1234} < (a_{1}^{*}+a_{1})(a_{2}^{*}+a_{2})(a_{3}^{*}+a_{3})(a_{4}^{*}+a_{4})></math> | <math>< S_{int}^{4}> =\int_{1234} < (a_{1}^{*}+a_{1})(a_{2}^{*}+a_{2})(a_{3}^{*}+a_{3})(a_{4}^{*}+a_{4})></math> | ||
| Line 301: | Line 326: | ||
<math>=6< a_{1}^{*}a_{2}^{*}a_{3}a_{4}>=6\int _{1234}\Delta ^{*}(1)\Delta ^{*}(2)\Delta(3)\Delta(4)< \psi_{\downarrow}(1)\psi_{\uparrow}(1)\psi_{\downarrow}(2)\psi_{\uparrow}(2)\psi_{\downarrow}^{*}(3)\psi_{\uparrow}^{*}(3)\psi_{\downarrow}^{*}(4)\psi_{\uparrow}^{*}(4)> </math> | <math>=6< a_{1}^{*}a_{2}^{*}a_{3}a_{4}>=6\int _{1234}\Delta ^{*}(1)\Delta ^{*}(2)\Delta(3)\Delta(4)< \psi_{\downarrow}(1)\psi_{\uparrow}(1)\psi_{\downarrow}(2)\psi_{\uparrow}(2)\psi_{\downarrow}^{*}(3)\psi_{\uparrow}^{*}(3)\psi_{\downarrow}^{*}(4)\psi_{\uparrow}^{*}(4)> </math> | ||
<math> | By Feynman diagram, <math>< S_{int}^{4}></math> has: | ||
[[Image:Secondorder.png]] | |||
[[Image:Square.png]] | |||
<math>3< S_{int}^{2}> ^{2}=3\int_{1,2}2< a_{1}^{*}a_{2}> \int_{3,4}2< a_{3}^{*}a_{4}>=12\int_{1,2,3,4}\Delta ^{*}(1)\Delta ^{*}(2)\Delta(3)\Delta(4)< \psi_{\downarrow}(1)\psi_{\uparrow}(1)\psi_{\uparrow}^{*}(3)\times</math> | |||
<math>\psi_{\downarrow}^{*}(3)>< \psi_{\downarrow}(2)\psi_{\uparrow}(2)\psi_{\uparrow}^{*}(4)\psi_{\downarrow}^{*}(4)></math> | |||
<math>-2G(2-3) G(2-4)G(1-4)G(1-3)=-12\int_{1,2,3,4}\Delta ^{*}(1)\Delta _{*}(2)\Delta (3)\Delta (4)G(2-3)G(2-4)G(1-4)G(1-3)</math> | <math>-2G(2-3) G(2-4)G(1-4)G(1-3)=-12\int_{1,2,3,4}\Delta ^{*}(1)\Delta _{*}(2)\Delta (3)\Delta (4)G(2-3)G(2-4)G(1-4)G(1-3)</math> | ||
Recall | Recall the Fourier transform of one body Green function is: | ||
<math>G(2-3)=< \psi (r_{2},\tau _{2})\psi ^{*}(r_{3},\tau _{3})>=\frac{1}{\beta } \sum_{\omega _{n}}\frac{1}{L^{D}}\sum_{k}e^{-i\omega _{n}(\tau _{2}-\tau _{3})}e^{ik.(r_{2}-r_{3})}\frac{1}{-i\omega _{n}+\epsilon _{k}-\mu }</math> | <math>G(2-3)=< \psi (r_{2},\tau _{2})\psi ^{*}(r_{3},\tau _{3})>=\frac{1}{\beta } \sum_{\omega _{n}}\frac{1}{L^{D}}\sum_{k}e^{-i\omega _{n}(\tau _{2}-\tau _{3})}e^{ik.(r_{2}-r_{3})}\frac{1}{-i\omega _{n}+\epsilon _{k}-\mu }</math> | ||
To seek solution of which are <math>\tau</math> independent using Feynman diagram | |||
<math>\frac{1}{\beta ^{4}}\sum_{\omega _{{n}_{1}}}...\sum_{\omega _{{n}_{4}}}\int_{0}^\beta {d\tau_{1}}\int_{0}^\beta {d\tau_{2}} \int_{0}^\beta {d\tau_{3}} \int_{0}^\beta {d\tau_{4}}e^{-i\omega _{{n}_{1}}(\tau _{1}-\tau _{3})} e^{-i\omega _{{n}_{2}}(\tau _{1}-\tau _{4})}e^{-i\omega _{{n}_{3}}(\tau _{2}-\tau _{3})}e^{-i\omega _{{n}_{4}}(\tau _{2}-\tau _{4})} G(i\omega _{{n}_{1}},r_{1}-r_{3})G(i\omega _{{n}_{2}},r_{1}-r_{4})G(i\omega _{{n}_{3}},r_{2}-r_{3})G(i\omega _{{n}_{4}},r_{2}-r_{4}) | <math>\frac{1}{\beta ^{4}}\sum_{\omega _{{n}_{1}}}...\sum_{\omega _{{n}_{4}}}\int_{0}^\beta {d\tau_{1}}\int_{0}^\beta {d\tau_{2}} \int_{0}^\beta {d\tau_{3}} \int_{0}^\beta {d\tau_{4}}e^{-i\omega _{{n}_{1}}(\tau _{1}-\tau _{3})} e^{-i\omega _{{n}_{2}}(\tau _{1}-\tau _{4})}e^{-i\omega _{{n}_{3}}(\tau _{2}-\tau _{3})}e^{-i\omega _{{n}_{4}}(\tau _{2}-\tau _{4})} G(i\omega _{{n}_{1}},r_{1}-r_{3})\times</math> | ||
</math> | |||
<math>G(i\omega _{{n}_{2}},r_{1}-r_{4})G(i\omega _{{n}_{3}},r_{2}-r_{3})G(i\omega _{{n}_{4}},r_{2}-r_{4})</math> | |||
after getting integration over <math>\tau_{1}</math> we will get <math>\beta \delta (\omega _{n_{1}},-\omega _{n_{2}}) </math> and similarly by getting integration over <math>\tau_{2}</math> we have <math>\beta \delta (\omega _{n_{3}},-\omega _{n_{4}}) </math> | after getting integration over <math>\tau_{1}</math> we will get <math>\beta \delta (\omega _{n_{1}},-\omega _{n_{2}}) </math> and similarly by getting integration over <math>\tau_{2}</math> we have <math>\beta \delta (\omega _{n_{3}},-\omega _{n_{4}}) </math> | ||
| Line 338: | Line 371: | ||
<math>r_{2}-r_{4}=\frac{1}{2}(\mu _{1,4}+\mu_{2,3})-\mu</math> | <math>r_{2}-r_{4}=\frac{1}{2}(\mu _{1,4}+\mu_{2,3})-\mu</math> | ||
<math>\simeq -12\int d^{D}R d^{D}\mu d^{D}\mu_{1.4}d^{D}\mu_{2,3}\Delta ^{\ast }(R)\Delta^{\ast } (R)\Delta (R)\Delta (R)\sum_{\omega _n}G(i\omega _{n},\mu +\frac{1}{2}(\mu_{1,4}+\mu _{2,3}))G(-i\omega _{n},\mu _{1,4})\times</math> | |||
<math>G(-i\omega _{n},\mu _{2,3})G(i\omega _{n},\mu +\frac{1}{2}(\mu_{1,4}+\mu _{2,3}))</math> | |||
integrate over<math>\mu</math> gives us: <math>L^{D}</math> <math>\delta_{k_{1},k_{4}}</math> | |||
and similarly <math>\mu_{1,4}</math>: <math>L^{D}</math> <math>\delta_{k_{1},-k_{2}}</math> | |||
<math>\mu_{2,3}</math> <math>l^{D}</math> <math>\delta_{k_{1},-k_{3}}</math> | |||
<math>-12\int d^{D}R\left | \Delta (R)^{4} \right |\sum_{\omega _{n}}\frac{1}{L^{D}}\sum_{k}\frac{1}{(-i\omega _{n}+\varepsilon_{k}-\mu)^{2}}\frac{1}{(i\omega _{n}+\varepsilon_{-k}+\mu)^{2}}</math> | |||
<math>\epsilon _{k}=\epsilon _{-k}</math> because of timereversal symetry. | |||
<math>\epsilon _{k}-\mu =\xi </math> | |||
[[Image:Contour-yp.png]] | |||
<math>-12\int d^{D}R\left | \Delta (R)\right |^{4}\sum_{\omega_{n}}\int_{-\infty }^{+\infty | |||
}d\xi N(\xi +\mu )\frac{1}{(-i\omega _{n}+\xi )^{2}}\frac{1}{(i\omega _{n}+\xi )^{2}} </math> | |||
<math>I(p,q)=\int_{-\infty }^{+\infty }d\xi \frac{1}{(\xi -p)^{2}}\frac{1}{(\xi +p)^{2}}={\frac{\partial }{\partial p}}\int d\xi \frac{1}{\xi -p}\frac{1}{(\xi +p)^{2}} | |||
</math> | |||
<math>\frac{\partial }{\partial p}2\pi i \frac{1}{(p+q)^{2}}=2\pi i\frac{-2}{(p+q)^{2}}</math> | |||
<math>\simeq -12\int d^{D}R\left | \Delta (R) \right |^{4}\sum_{\omega _{n}}N(0)\frac{-4\pi i}{(2i\omega _{n})^{3}} </math> | |||
<math>\simeq-12\beta\int d^{D}R\mid\triangle(R)\mid^{4}\frac{N(0)}{2\beta}\pi\frac{\beta^{3}}{\pi^{3}}\sum_{n=-\infty}^{\infty}\frac{1}{\mid2n+1\mid^{3}}</math> | |||
We can substitute the sum using | |||
<math>\sum_{n=-\infty}^{\infty}\frac{1}{\mid2n+1\mid^{3}}=2\times\frac{7\xi(3)}{8}</math> | |||
<math>=-\frac{1}{2}\frac{7\xi(3)}{8\pi^{2}}\beta^{2}N(0)\frac{1}{K_{B}T}\int d^{D}R\mid\triangle(R)\mid^{4}</math> | |||
So, we get a term that is always negative and it corresponds to the <math>\mid\psi(r)\mid^{4}</math> in the Ginzberg-Landauer functional. | |||
=== Saddle Point Approximation === | |||
| Line 414: | Line 485: | ||
<math>c_{V}^{(n)}=\frac{\partial}{\partial T}\left(2(from\; spin)\int\frac{d^{D}k}{(2\pi)^{D}}\frac{\left(\epsilon_{k}-\mu\right)}{e^{\frac{\epsilon_{k}-\mu}{k_{B}T}+1}}\right)</math> | <math>c_{V}^{(n)}=\frac{\partial}{\partial T}\left(2(from\; spin)\int\frac{d^{D}k}{(2\pi)^{D}}\frac{\left(\epsilon_{k}-\mu\right)}{e^{\frac{\epsilon_{k}-\mu}{k_{B}T}+1}}\right)</math> | ||
<math>=2\int\frac{d^{D}k}{(2\pi)^{D}}\frac{-\left(\epsilon_{k}-\mu\right)}{\left(e^{\frac{\epsilon_{k}-\mu}{k_{B}T}+1}\right)^{2}}\left(\frac{-\left(\epsilon_{k}-\mu\right)}{k_{B}T^{2}}\right)e^{\left(\frac{\epsilon_{k}-\mu}{k_{B}T}\right)}</math> | <math>=2\int\frac{d^{D}k}{(2\pi)^{D}}\frac{-\left(\epsilon_{k}-\mu\right)}{\left(e^{\frac{\epsilon_{k}-\mu}{k_{B}T}+1}\right)^{2}}\left(\frac{-\left(\epsilon_{k}-\mu\right)}{k_{B}T^{2}}\right)e^{\left(\frac{\epsilon_{k}-\mu}{k_{B}T}\right)}</math> <math>\simeq2k_{B}N(0)\int_{-\infty}^{\infty}d\xi\left(\frac{\xi}{2k_{B}T}\right)^{2}\frac{1}{cosh^{2}\left(\frac{\xi}{2k_{B}T}\right)}</math> | ||
<math>\simeq4k_{B}^{2}TN(0)\underset{\frac{\pi^{2}}{6}}{\underbrace{\int_{-\infty}^{\infty}dx\frac{x^{2}}{cosh^{2}x}}}=\frac{2\pi^{2}}{3}k_{B}^{2}T</math> | <math>\simeq4k_{B}^{2}TN(0)\underset{\frac{\pi^{2}}{6}}{\underbrace{\int_{-\infty}^{\infty}dx\frac{x^{2}}{cosh^{2}x}}}=\frac{2\pi^{2}}{3}k_{B}^{2}T</math> | ||
| Line 460: | Line 530: | ||
|94% | |94% | ||
|} | |} | ||
Experimental data for Aluminum gives | |||
<math>\frac{\Delta c_{V}}{c_{V}^{(n)}}\simeq 1.39</math> | |||
This result from the saddle point approximation/mean field is very close to the experimental result. But for high Tc superconductor the behavior is very different. The heat capacity of superconductor decrease gradually, doesn't have sharp jump like in the picture below. The Gaussian approximation we have used is not enough to explain high Tc superconductor. | |||
=== Limitation of Microscopic derivation of the Ginzburg-Landau functional === | |||
[[image:Cv.png|thumb|400px|middle|Experimental result of heat capacity of aluminum (dotted lines), at zero magnetic field(curve peak) and at 300 Gauss when superconductivity suppressed (no peak) , typical curve for high Tc superconductor (additional solid blue line), (Phys. Rev., 114:676–685, 1959)]] | |||
1) Fluctuation is important in low dimension (such in 2D by including Gaussian fluctuation) | |||
2) In 1D, beyond mean field approach is needed | |||
3) Mean Field give jump in second order of the derivative | |||
4) We need to include fluctuation in High Tc superconductor | |||
5) Gaussian approximation is not enough in High Tc superconductor | |||
== Effects of an applied magnetic field; Type I and Type II superconductivity == | == Effects of an applied magnetic field; Type I and Type II superconductivity == | ||
| Line 528: | Line 620: | ||
We can now immediately write down the variational derivative, which, upon being set to zero, gives us the first GL equation, | We can now immediately write down the variational derivative, which, upon being set to zero, gives us the first GL equation, | ||
<math>\frac{1}{2m}\left (\frac{\hbar}{i}\nabla-\frac{2e}{c}\vec{A}\right )^2\Psi+\alpha(T-T_c)\Psi+b|\Psi|^2\Psi=0.</math> | <math>\frac{1}{2m}\left (\frac{\hbar}{i}\nabla-\frac{2e}{c}\vec{A}\right )^2\Psi+\alpha(T-T_c)\Psi+b|\Psi|^2\Psi=0.</math> | ||
We also need to minimize the free energy with respect to the magnetic field. We have already done this for the normal case, and there is only one more term that we need to consider in the superconducting case; we will therefore only treat this term. We can quickly write down the variation in the superconducting part of the free energy <math>F_{SC}</math>, which is | We also need to minimize the free energy with respect to the magnetic field. We have already done this for the normal case, and there is only one more term that we need to consider in the superconducting case; we will therefore only treat this term. We can quickly write down the variation in the superconducting part of the free energy <math>F_{SC}</math>, which is | ||
| Line 540: | Line 632: | ||
or, introducing <math>\vec{B}</math> and <math>\vec{H}</math>, | or, introducing <math>\vec{B}</math> and <math>\vec{H}</math>, | ||
<math>\frac{e}{m}\left (\Psi^{*}\frac{\hbar}{i}\nabla\Psi-\Psi\frac{\hbar}{i}\nabla\Psi^{*}\right )-\frac{4e^2}{mc}|\Psi|^2\vec{A}=\frac{c}{4\pi}\nabla\times(\vec{B}-\vec{H}).</math> | <math>\frac{e}{m}\left (\Psi^{*}\frac{\hbar}{i}\nabla\Psi-\Psi\frac{\hbar}{i}\nabla\Psi^{*}\right )-\frac{4e^2}{mc}|\Psi|^2\vec{A}=\frac{c}{4\pi}\nabla\times(\vec{B}-\vec{H}).</math> | ||
Given the definition of <math>\vec{H}</math> and the Maxwell equation (assuming static fields), | Given the definition of <math>\vec{H}</math> and the Maxwell equation (assuming static fields), | ||
| Line 606: | Line 698: | ||
In terms of these, the first GL equation becomes | In terms of these, the first GL equation becomes | ||
<math>\left (-\frac{i}{\kappa}\tilde{\nabla}-\tilde{A}\right )^2\psi+(\left |\psi\right |^2-1)\psi=0</math> | <math>\left (-\frac{i}{\kappa}\tilde{\nabla}-\tilde{A}\right )^2\psi+(\left |\psi\right |^2-1)\psi=0</math> | ||
and the second becomes | and the second becomes | ||
<math>\frac{1}{2\kappa}\left (\psi^{\ast}\frac{\tilde{\nabla}}{i}\psi-\psi\frac{\tilde{\nabla}}{i}\psi^{\ast}\right )-\left |\psi\right |^2\vec{A}=\tilde{\nabla}\times[\tilde{\nabla}\times(\tilde{A}-\tilde{A}_0)].</math> | <math>\frac{1}{2\kappa}\left (\psi^{\ast}\frac{\tilde{\nabla}}{i}\psi-\psi\frac{\tilde{\nabla}}{i}\psi^{\ast}\right )-\left |\psi\right |^2\vec{A}=\tilde{\nabla}\times[\tilde{\nabla}\times(\tilde{A}-\tilde{A}_0)].</math> | ||
We see that our theory has a dimensionless parameter in it, namely <math>\kappa</math>, which is known as the Ginzburg-Landau parameter. We may write this parameter as | We see that our theory has a dimensionless parameter in it, namely <math>\kappa</math>, which is known as the Ginzburg-Landau parameter. We may write this parameter as | ||
| Line 624: | Line 716: | ||
We may now find the value of this parameter in the microscopic model we considered earlier. In that case, we found that | We may now find the value of this parameter in the microscopic model we considered earlier. In that case, we found that | ||
<math>\frac{\hbar^2}{2m}=N(\mu)\xi^2=N(\mu)\frac{7\zeta(3)}{16\pi^2 d} | <math>\frac{\hbar^2}{2m}=N(\mu)\xi^2=N(\mu)\frac{7\zeta(3)}{16\pi^2 d}\ell_T^2,</math> | ||
where <math>N(\mu)</math> is the density of states at the Fermi level, <math>\xi</math> is the coherence length, <math>d</math> is the number of dimensions that we are working in, and <math>l_T</math> is the thermal wavelength. We will state the result for <math>d=3</math>. Given that | where <math>N(\mu)</math> is the density of states at the Fermi level, <math>\xi</math> is the coherence length, <math>d</math> is the number of dimensions that we are working in, and <math>l_T</math> is the thermal wavelength. We will state the result for <math>d=3</math>. Given that | ||
<math> | <math>\ell_T=\frac{\hbar v_F}{k_B T}</math> | ||
and that, in this case, | and that, in this case, | ||
| Line 650: | Line 742: | ||
<math>\kappa=(0.04 - 1.3)\cdot\frac{T_c\,[\text{K}]}{\sqrt{E_F\,[\text{eV}]}}.</math> | <math>\kappa=(0.04 - 1.3)\cdot\frac{T_c\,[\text{K}]}{\sqrt{E_F\,[\text{eV}]}}.</math> | ||
=== A Simple Example - The Strongly Type-I Superconductor === | === A Simple Example - The Strongly Type-I Superconductor With a Planar Surface === | ||
As a simple demonstration of the solution of the GL equations, let us consider a strongly Type I (<math>\kappa\ll 1</math>) superconductor with a planar boundary between it and an insulator. Let us set up our coordinate system so that the boundary is at <math>x=0</math>. | As a simple demonstration of the solution of the GL equations, let us consider a strongly Type I (<math>\kappa\ll 1</math>) superconductor with a planar boundary between it and an insulator. Let us set up our coordinate system so that the boundary is at <math>x=0</math>. | ||
| Line 706: | Line 798: | ||
<math>\frac{d^2\tilde{B}}{d\tilde{x}^2}=0.</math> | <math>\frac{d^2\tilde{B}}{d\tilde{x}^2}=0.</math> | ||
The solution, in terms of dimensional quantities, is <math>B(x)=B_0+B_1 x</math>. We must set <math>B_1=0</math> so that the field does not increase indefinitely as we move away from the superconductor. Since <math>\vec{B}=\vec{H}</math> in the normal state, we conclude that <math>B(x)=H</math> for <math>x>0</math>. | The solution, in terms of dimensional quantities, is <math>B(x)=B_0+B_1 x</math>. We must set <math>B_1=0</math> so that the field does not increase indefinitely as we move away from the superconductor. Since <math>\vec{B}=\vec{H}</math> in the normal state, we conclude that <math>B(x)=H</math> for <math>x>0</math>. The following is a plot of the full dependence of the magnetic field on position. | ||
[[Image:SC_BField_PlanarInt.PNG]] | |||
We have now shown why we called <math>\lambda</math> the penetration depth; it sets the length scale over which the magnetic field tends to zero inside the superconductor. We have also illustrated the expulsion of applied magnetic fields from the | We have now shown why we called <math>\lambda</math> the penetration depth; it sets the length scale over which the magnetic field tends to zero inside the superconductor. We have also illustrated the expulsion of applied magnetic fields from the bulk of a Type I superconductor; this is known as the Meissner effect. | ||
=== Thermodynamics of Type-I Superconductors in Magnetic Fields === | === Thermodynamics of Type-I Superconductors in Magnetic Fields === | ||
| Line 716: | Line 810: | ||
<math>f_s=\alpha(T-T_c)\Psi_0^2+\tfrac{1}{2}b\Psi_0^4=-\frac{\alpha^2}{2b}(T-T_c)^2.</math> | <math>f_s=\alpha(T-T_c)\Psi_0^2+\tfrac{1}{2}b\Psi_0^4=-\frac{\alpha^2}{2b}(T-T_c)^2.</math> | ||
== | This is known as the condensation energy (per unit volume). We see that we can "save" energy by going into the superconducting state. | ||
In the normal state, only the magnetic field terms are present, so that the free energy is | |||
<math>F_n=\int d^d\vec{r}\,\left [\frac{1}{8\pi}(\nabla\times\vec{A})^2-\frac{1}{c}\vec{J}_\text{ext}\cdot\vec{A}\right ].</math> | |||
We may substitute in | |||
<math>\frac{4\pi}{c}\vec{J}_\text{ext}=\nabla\times\vec{H}</math> | |||
to get | |||
<math>F_n=\int d^d\vec{r}\,\left [\frac{1}{8\pi}(\nabla\times\vec{A})^2-\frac{1}{4\pi}(\nabla\times\vec{H})\cdot\vec{A}\right ]=\int d^d\vec{r}\,\left [\frac{1}{8\pi}(\nabla\times\vec{A})^2-\frac{1}{4\pi}(\nabla\times\vec{A})\cdot\vec{H}\right ] | |||
=\int d^d\vec{r}\,\left [\frac{1}{8\pi}B^2-\frac{1}{4\pi}\vec{B}\cdot\vec{H}\right ].</math> | |||
In the normal state, <math>\vec{B}=\vec{H}</math>, so | |||
<math>F_n=-\int d^d\vec{r}\,\frac{1}{8\pi}H^2.</math> | |||
The free energy per unit volume of the normal state is therefore | |||
<math>f_n=-\frac{1}{8\pi}H^2.</math> | |||
We see that, overall, we also "save" energy in the normal state. Which state we go into depends on which "saves" more energy. We may now define a field at which the "savings" are the same for both states; this is the (thermodynamic) critical field <math>H_c</math> (sometimes also denoted <math>H_{cm}</math>). Equating the free energies per unit volume of each state, we obtain | |||
<math>\frac{\alpha^2}{2b}(T-T_c)^2=\frac{1}{8\pi}H_c^2,</math> | |||
or, solving for <math>H_c</math>, | |||
<math>H_c=\sqrt{\frac{4\pi}{b}}\alpha\left |T-T_c\right |.</math> | |||
We see, therefore, that GL theory predicts a linear dependence of the critical field on the temperature. This is not what is observed experimentally, however. The dependence of the critical field on temperature in many real superconductors can, in fact, be modeled with the following empirical law: | |||
<math>H_c(T)=H_c(0)\left [1-\left (\frac{T}{T_c}\right )^2\right ].</math> | |||
We plot this relation below. | |||
[[Image:CriticalField_vs_T.PNG]] | |||
We see that, near <math>T_c</math>, the dependence of the critical field on temperature does indeed follow the linear relation that we just derived. However, it deviates from said relation when we go far below <math>T_c</math>. This is not surprising; the GL theory from which we obtained the linear relation is only valid near <math>T_c</math>. In order to obtain a more accurate relation, we require a theory for the superconductor that is valid far below <math>T_c</math>. | |||
We may rewrite our dimensionless vector potential and magnetic field in terms of the critical field. We may write our expression for <math>H_c</math> as | |||
<math>H_c^2=4\pi b\left |\Psi_0\right |^4.</math> | |||
Our dimensionless vector potential is then | |||
<math>\tilde{A}=\frac{2e}{c}\frac{\Psi_0}{\sqrt{2mb\Psi_0^4}}\vec{A}=\frac{2e}{c}\Psi_0\sqrt{\frac{4\pi}{2mH_c^2}}\vec{A}=\sqrt{\frac{8\pi e^2\Psi_0^2}{mc^2}}\vec{A}=\frac{1}{\sqrt{2}H_c \lambda}\vec{A}.</math> | |||
We may rewrite the definition of the magnetic field as | |||
<math>\vec{B}=\tilde{\nabla}\times\sqrt{2}H_c\tilde{A},</math> | |||
or | |||
<math>\tilde{\nabla}\times\tilde{A}=\frac{1}{\sqrt{2}H_c}\vec{B}=\tilde{B}.</math> | |||
=== Magnetic Properties of a Type-I Superconductor === | |||
In the approximation stated above, we find that, in the superconducting state (the applied magnetic field is below <math>H_c</math>), the total magnetic field <math>\vec{B}</math> is completely expelled, while <math>\vec{B}=\vec{H}</math> when the applied field is above <math>H_c</math>. From the defining relation for the magnetization <math>\vec{M}</math>, | |||
<math>\vec{B}=\vec{H}+4\pi\vec{M},</math> | |||
we find that the magnitude of the magnetization increases linearly with, and points in the opposite direction to, <math>\vec{H}</math>, in the superconducting state, but is zero in the normal state. We plot these two relations below. | |||
[[Image:SC_BvsHandMvsH.PNG]] | |||
We will now demonstrate two consequences of the total expulsion of a magnetic field from a superconductor. | |||
'''1) The total field is always tangential to the surface of a superconductor.''' | |||
First, recall the Maxwell equation, | |||
<math>\nabla\cdot\vec{B}=0.</math> | |||
Let us now consider the boundary between a superconductor and a normal region: | |||
[[Image:SC_BFieldCond_PillBox.PNG]] | |||
We will find the flux of a magnetic field through the "pill box" shown above. Let the area of the circular surfaces be <math>\Delta A</math>, and let us assume that the contribution from the "tube" part of the surface is negligible (we will assume that its height is small compared to the radius of the circular surfaces). Then the total flux may be written as | |||
<math>B_{n,\bot}\cdot\Delta A-B_{sc,\bot}\cdot\Delta A,</math> | |||
where <math>B_{n,\bot}</math> and <math>B_{sc,\bot}</math> are the components of the magnetic field normal to the circular surfaces of the "pill box" in the normal and superconducting regions, respectively. The Maxwell equation stated above is equivalent to the statement that the total flux through a closed surface, such as the "pill box" we consider here, must be zero. Therefore, | |||
<math>B_{n,\bot}=B_{sc,\bot}.</math> | |||
However, we know that the superconductor completely expels magnetic fields, so that <math>\vec{B}_{sc}=0</math>. Therefore, <math>B_{n,\bot}=0</math>, thus proving that <math>\vec{B}_n</math> can only have tangential components. | |||
'''2) As a direct consequence of (1), a type-I superconductor in an external magnetic field always carries an electrical current near its surface.''' | |||
To show this, first recall the Maxwell equation (Ampere's Law in the case of static fields), | |||
<math>\nabla\times\vec{B}=\frac{4\pi}{c}\vec{J},</math> | |||
or, in integral form, | |||
<math>\oint_{\partial S}\vec{B}\cdot d\vec{\ell}=\frac{4\pi}{c}I,</math> | |||
where <math>S</math> is a surface with bounding curve <math>\partial S</math>, the line integral on the left is taken in the direction that would cause a right-handed screw to advance in the direction of the normal to the surface, and <math>I</math> is the total current passing through the surface. | |||
Let us now, once again, consider the boundary between a superconductor and a normal region and a rectangular contour drawn around the boundary: | |||
[[Image:SC_BField_Contour.PNG]] | |||
In this case, because the magnetic field is zero in the superconducting region and because the magnetic field in the normal region is tangential to the surface of the superconductor, then, assuming that the lengths of segments 14 and 23 are small compared to that of segments 12 and 34. In this case, the left-hand side of the Maxwell equation becomes | |||
<math>\oint_{\partial S}\vec{B}\cdot d\vec{\ell}=B\ell_{12},</math> | |||
where <math>\ell_{12}</math> is the length of segment 12. The right-hand side, on the other hand, is | |||
<math>\frac{4\pi}{c}I=\frac{4\pi}{c}K\ell_{12},</math> | |||
where <math>K</math> is the surface current density (per unit length). This implies that | |||
<math>B=\frac{4\pi}{c}K,</math> | |||
or, in vector form, | |||
<math>\vec{K}=\frac{c}{4\pi}\hat{n}\times\vec{B},</math> | |||
where <math>\hat{n}</math> is the normal to the surface pointing into the normal region. In the case depicted above, we see that <math>\vec{K}</math> points into the page or screen. | |||
=== An Example: The Magnetic Field Around a Spherical Superconductor === | |||
These observations lead to interesting conclusions for superconductors with geometries more complex than a cylinder inside a magnetic field parallel to its axis. Consider, for example, a spherical superconductor, depicted below: | |||
[[Image:MagField_SCSphere.png]] | |||
As we can see, the magnetic field near the equator is stronger than the applied field, while the field at the poles vanishes. This implies that the magnetic field near the equator may exceed <math>H_c</math> even if the applied field is less than <math>H_c</math>, simply due to the geometry of the sample. In fact, for a certain range of fields, | |||
<math>(1-\eta)H_c<H<H_c,</math> | |||
the sample will enter an intermediate state, in which superconducting and normal regions coexist. The above inequality holds for any geometry, in fact, and <math>\eta</math> is known as the demagnetizing factor of the sample. Its value will depend on the exact geometry of the sample; we will now show that, for a sphere, <math>\eta=\tfrac{1}{3}</math>. We will do so by solving Maxwell's equations for a spherical superconductor of radius <math>R</math> in a uniform applied magnetic field <math>\vec{H}=H\hat{z}</math>. The boundary conditions for this problem are | |||
<math>\vec{B}(\vec{r})=H\hat{z}</math> | |||
for <math>|\vec{r}|\rightarrow\infty</math> and | |||
<math>\hat{n}\cdot\vec{B}(\vec{r})=0</math> | |||
on the surface of the sphere. Outside the superconductor, the equations satisfied by <math>\vec{B}</math> are | |||
<math>\nabla\cdot\vec{B}=0</math> | |||
and | |||
<math>\nabla\times\vec{B}=0.</math> | |||
The second equation implies that there are no current sources outside the superconductor. It also implies that we may write the magnetic field in terms of a scalar potential. We therefore write | |||
<math>\vec{B}=\nabla\Phi+H\vec{z}.</math> | |||
Substituting this into the first equation, we get | |||
<math>\nabla^2\Phi=0,</math> | |||
which is just Laplace's equation. Our boundary conditions for <math>\Phi</math> are, in spherical coordinates, | |||
<math>\Phi(\vec{r}\rightarrow\infty)=0</math> | |||
and | |||
<math>\frac{\partial\Phi}{\partial r}+H\cos{\theta}=0</math> | |||
on the surface. Laplace's equation in spherical coordinates is | |||
<math>\frac{1}{r^2}\frac{\partial}{\partial r}\left (r^2\frac{\partial\Phi}{\partial r}\right )+\frac{1}{r^2\sin{\theta}}\frac{\partial}{\partial\theta}\left (\sin{\theta}\frac{\partial\Phi}{\partial\theta}\right )+\frac{1}{r^2\sin^2{\theta}}\frac{\partial^2\Phi}{\partial\phi^2}=0.</math> | |||
Because our system has azimuthal symmetry, <math>\Phi</math> should be independent of <math>\phi</math>. Therefore, <math>\Phi(\vec{r})=\Phi(r,\theta)</math> and Laplace's equation becomes | |||
<math>\frac{1}{r^2}\frac{\partial}{\partial r}\left (r^2\frac{\partial\Phi}{\partial r}\right )+\frac{1}{r^2\sin{\theta}}\frac{\partial}{\partial\theta}\left (\sin{\theta}\frac{\partial\Phi}{\partial\theta}\right )=0.</math> | |||
Multiplying by <math>r^2</math>, we get | |||
<math>\frac{\partial}{\partial r}\left (r^2\frac{\partial\Phi}{\partial r}\right )+\frac{1}{\sin{\theta}}\frac{\partial}{\partial\theta}\left (\sin{\theta}\frac{\partial\Phi}{\partial\theta}\right )=0.</math> | |||
We will now attempt to solve this equation by separation of variables. Let us try a solution of the form | |||
<math>\Phi(r,\theta)=R(r)\chi(\theta).</math> | |||
Then | |||
<math>\frac{1}{R}\frac{d}{dr}\left (r^2\frac{dR}{dr}\right )=-\frac{1}{\chi}\frac{1}{\sin{\theta}}\frac{d}{d\theta}\left (\sin{\theta}\frac{d\chi}{d\theta}\right ).</math> | |||
We see that we have an expression depending only on <math>r</math> on one side and one depending only on <math>\theta</math> on the other. The only way for this equation to be satisfied is if both equal a constant, which we will call <math>-\lambda</math>. Let us first consider the equation for <math>\chi</math>. This equation is | |||
<math>\frac{1}{\sin{\theta}}\frac{d}{d\theta}\left (\sin{\theta}\frac{d\chi}{d\theta}\right )=\lambda\chi.</math> | |||
If we make the substitution, <math>x=\cos{\theta}</math>, into this equation, we get | |||
<math>\frac{d}{dx}\left [(1-x^2)\frac{d\chi}{dx}\right ]=\lambda\chi.</math> | |||
We recognize this as the Legendre differential equation. The only physically interesting solutions to this equation occur when <math>\lambda=-l(l+1)</math>, in which case we find that <math>\chi</math> is a Legendre polynomial, | |||
<math>\chi(\theta)=P_l(\cos{\theta}).</math> | |||
The first few Legendre polynomials are <math>P_0(x)=1</math>, <math>P_1(x)=x</math>, and <math>P_2(x)=\tfrac{1}{2}(3x^2-1)</math>. | |||
Now we will consider the equation for <math>R</math>. If we take <math>\chi(\theta)=P_l(\cos{\theta})</math>, then our differential equation for <math>R</math> becomes | |||
<math>\frac{d}{dr}\left (r^2\frac{dR}{dr}\right )=l(l+1)R,</math> | |||
or | |||
<math>\frac{d^2 R}{dr^2}+2r\frac{dR}{dr}-l(l+1)R=0.</math> | |||
This is an Euler-Cauchy differential equation. Let us assume a power law dependence for <math>R</math>, | |||
<math>R(r)=r^\alpha.</math> | |||
The equation becomes | |||
<math>\alpha(\alpha-1)r^\alpha+2\alpha r^\alpha-l(l+1)r^\alpha=0.</math> | |||
The exponent <math>\alpha</math> must therefore satisfy | |||
<math>\alpha(\alpha+1)=l(l+1).</math> | |||
This equation has two possible solutions, <math>\alpha=l</math> and <math>\alpha=-(l+1)</math>, so the general solution for the differential equation is | |||
<math>R(r)=A_l r^l+\frac{B_l}{r^{l+1}}.</math> | |||
The general solution to the original partial differential equation is then a linear combination of all possible products <math>R(r)\chi(\theta)</math>, | |||
<math>\Phi(r,\theta)=\sum_{l=0}^{\infty}\left (A_l r^l+\frac{B_l}{r^{l+1}}\right )P_l(\cos{\theta}).</math> | |||
Since <math>r^l\rightarrow\infty</math> for all <math>l>0</math>, we must set <math>A_l=0</math> for all such values of <math>l</math>. We will also set <math>A_0=0</math>, so that | |||
<math>\Phi(r,\theta)=\sum_{l=0}^{\infty}\frac{B_l}{r^{l+1}}P_l(\cos{\theta}).</math> | |||
We now apply the boundary condition, | |||
<math>\frac{\partial\Phi}{\partial r}+H\cos{\theta}=0,</math> | |||
to obtain | |||
<math>\sum_{l=0}^{\infty}\frac{(l+1)B_l}{R^{l+2}}P_l(\cos{\theta})=H\cos{\theta}.</math> | |||
By inspection, we find that <math>B_l=0</math> for all <math>l\neq 1</math>. For <math>l=1</math>, we have | |||
<math>B_l=\tfrac{1}{2}HR^3.</math> | |||
Therefore, the solution for <math>\Phi</math> is | |||
<math>\Phi(r,\theta)=\frac{HR^3}{2r^2}\cos{\theta},</math> | |||
and thus <math>\vec{B}</math> is | |||
<math>\vec{B}=\tfrac{1}{2}HR^3\nabla\left (\frac{\cos{\theta}}{r^2}\right )+H\hat{z}.</math> | |||
In spherical coordinates, the gradient operator is given by | |||
<math>\nabla\Phi=\frac{\partial\Phi}{\partial r}\hat{r}+\frac{1}{r}\frac{\partial\Phi}{\partial\theta}\hat{\theta}+\frac{1}{r\sin{\theta}}\frac{\partial\Phi}{\partial\phi}\hat{\phi},</math> | |||
so | |||
<math>\vec{B}=-H\left (\frac{R}{r}\right )^3(\cos{\theta}\hat{r}+\tfrac{1}{2}\sin{\theta}\hat{\theta})+H\hat{z}.</math> | |||
We recognize that <math>\hat{z}=\cos{\theta}\hat{r}-\sin{\theta}\hat{\theta}</math>, so that | |||
<math>\vec{B}=\left [1-\left (\frac{R}{r}\right )^3\right ]H\cos{\theta}\hat{r}-\left [1+\tfrac{1}{2}\left (\frac{R}{r}\right )^3\right ]H\sin{\theta}\hat{\theta}.</math> | |||
We now want to find the point at which the magnetic field has the largest magnitude. The magnitude of this vector is given by | |||
<math>|\vec{B}|^2=H^2\left [1+\tfrac{1}{2}\left (\frac{R}{r}\right )^3\right ]^2+3\left (\frac{R}{r}\right )^3\left [\tfrac{1}{4}\left (\frac{R}{r}\right )^3-1\right ]\cos^2{\theta}</math> | |||
We see that the second term, which is proportional to <math>\cos^2{\theta}</math>, is clearly negative when <math>r>R</math>. Therefore, we must make the size of this term as small as possible. This may be done by letting <math>\theta=\tfrac{\pi}{2}</math>. For this value of <math>\theta</math>, we have | |||
<math>|\vec{B}|^2=H^2\left [1+\tfrac{1}{2}\left (\frac{R}{r}\right )^3\right ]^2.</math> | |||
This function is monotonically decreasing as we increase <math>r</math>; therefore, we choose the smallest possible value of <math>r</math>, which is <math>r=R</math>. This gives us | |||
<math>|\vec{B}|^2=\tfrac{9}{4}H^2,</math> | |||
or <math>|\vec{B}|=\tfrac{3}{2}H</math>. Therefore, the total magnetic field achieves its maximum magnitude at the equator of the sphere, where it is three halves the applied field. Therefore, if the applied field is larger than <math>H=\tfrac{2}{3}H_c</math>, the field at the equator would become larger than <math>H_c</math>, which would destroy the sphere's superconductivity at that point. Therefore, the sphere enters an intermediate state when <math>\tfrac{2}{3}H_c<H<H_c</math>, so that the demagnetizing factor <math>\eta=\tfrac{1}{3}</math>. | |||
=== Superconductors of General Geometries === | |||
In general, the maximum magnetic field on the surface of a superconductor will be related to the applied field by | |||
<math>B_{\text{max}}=\frac{H}{1-\eta}.</math> | |||
We will now list the values of <math>\eta</math> for a few different geometries. | |||
{| border="1" align="center" style="text-align:center;" | |||
|'''Geometry''' | |||
|'''Demagnetizing factor <math>\eta</math>''' | |||
|- | |||
|Cylinder with <math>\vec{H}</math> parallel to its axis | |||
|<math>0</math> | |||
|- | |||
|Cylinder with <math>\vec{H}</math> perpendicular to its axis | |||
|<math>\tfrac{1}{2}</math> | |||
|- | |||
|Sphere | |||
|<math>\tfrac{1}{3}</math> | |||
|- | |||
|Infinite thin plate with <math>\vec{H}</math> perpendicular to the plate | |||
|<math>1</math> | |||
|} | |||
The sample will enter the intermediate state at the value of <math>H=H^{\ast}</math> at which <math>B_{\text{max}}=H_c</math>, which is | |||
<math>H^{\ast}=(1-\eta)H_c.</math> | |||
Therefore, the superconductor will be in the intermediate state when | |||
<math>(1-\eta)H_c<H<H_c.</math> | |||
We will now show plots of the magnetic field of a sphere at the equator and at the pole as a function of the applied field (for details on how to derive the dependence in the intermediate state, see P. G. DeGennes, ''Superconductivity of Metals and Alloys''). | |||
[[Image:BField_SCSphere.PNG]] | |||
In the intermediate state, the energy per volume of both the normal and superconducting states is the same. Therefore, the energy per unit ''area'' of a "domain wall" will be the dominant contribution. | |||
=== Surface Term of the Free Energy === | |||
The free energy in the reduced units can be written as | |||
<math>F=\int d^3 r \,\left[\alpha (T-T_c)|\Psi|^2 + \frac{b}{2} |\Psi|^4 + \frac{\hbar^2}{2m} |(\nabla | |||
- \frac{2ei}{\hbar c}\vec{A})\Psi|^2 + \frac{1}{8\pi}(\nabla\times\vec{A})^2 - \frac{1}{4\pi}\vec{H}\cdot\vec{B}\right]</math> | |||
<math>=\lambda^D\int d^D\tilde{r}\,\left[\alpha (T-T_c)|\Psi_o|^2 |\psi|^2 + \frac{b}{2} |\Psi_o|^4 |\psi|^4 + | |||
\frac{\hbar^2}{2m_{GL}}|\Psi_o|^2|(\frac{1}{\lambda}\tilde{\nabla}-\frac{2ei}{\hbar c}\sqrt{2}\lambda H_c \tilde{A})\psi|^2 + \frac{1}{8\pi \lambda^2} (\sqrt{2}\lambda H_c)^2 (\tilde{\nabla}\times\tilde{A})^2 | |||
- \frac{2\lambda^2 H_c^2}{4\pi \lambda^2} \tilde{H}\cdot\tilde{B}\,\right]</math> | |||
where | |||
<math>\tilde{r}=\frac{r}{\lambda}, \tilde{H}=\frac{H}{\sqrt{2}H_c}</math> | |||
Using the following relations: | |||
<math>b|\Psi_o|^4 = \frac{H_c^2}{4\pi}</math> | |||
<math>\frac{\alpha (T-T_c)}{b|\Psi_o|^2} = -1</math> | |||
<math>|\Psi_o|^2 \frac{4e^2}{mc^2} = \frac{1}{4\pi\lambda^2}</math> | |||
one has | |||
<math>F=\frac{\lambda^D H_c^2}{4\pi}\int d^D\tilde{r}\,\left[-|\psi|^2+\frac{1}{2}|\psi|^4+|(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})\psi|^2+\tilde{B}^2-2\tilde{H}\cdot\tilde{B}\,\right]</math> | |||
Now let's consider the gradinet term: | |||
<math>|(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})\psi|^2 | |||
= \,\left[ (\frac{-1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})\psi^*\,\right]\,\left[ (\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})\psi\,\right] | |||
= (-\tilde{A}\psi^*)(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})\psi | |||
- (\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}\psi^*)(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})\psi | |||
</math> | |||
Integration by part leads the 2nd term to the form: | |||
<math>-\tilde{\nabla}\cdot(\frac{1}{\kappa}\frac{1}{i}\psi^*(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})\psi) | |||
+ \psi^*(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})\psi)</math> | |||
where the 1st term needs to be evaluated on the surface where it vanishes by the boundary condition for an insulating interface. Hence the gradient term becomes | |||
<math>|(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})\psi|^2 | |||
= \psi^*(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})^2\psi</math> | |||
Assuming that <math>\psi</math> and <math>\tilde{A}</math> satisfy the GL equation, namely, | |||
<math>(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})^2 \psi = \psi - \psi |\psi|^2</math> | |||
we have | |||
<math>\psi^*(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})^2\psi = |\psi|^2-|\psi|^4</math> | |||
and the free energy becomes | |||
<math>F=\frac{\lambda^D H_c^2}{4\pi}\int d^D \tilde{r} \,\left[-\frac{1}{2}|\psi|^4+\tilde{B}^2-2\tilde{H}\cdot\tilde{B}\,\right]</math> | |||
This is true at the saddle point. Now the free energy for the normal state and the superconducting state are given by | |||
<math>F_n=\frac{\lambda^D H_c^2}{4\pi}\int d^D \tilde{r} \,\left[-\tilde{H}^2\,\right]</math> | |||
and | |||
<math>F_s=\frac{\lambda^D H_c^2}{4\pi}\int d^D \tilde{r} \,\left[-\frac{1}{2}|\psi|^4+\tilde{B}^2-2\tilde{B}\cdot\tilde{H}\,\right]</math> | |||
Therefore, the surface free energy of the interface is | |||
<math>F_s-F_n=\frac{\lambda^D H_c^2}{4\pi}\int d^D \tilde{r} \,\left[-\frac{1}{2}|\psi|^4+\tilde{B}^2-2\tilde{B}\cdot\tilde{H}+\tilde{H}^2\,\right] | |||
= \frac{\lambda^D H_c^2}{4\pi}\int d^D \tilde{r} \,\left[-\frac{1}{2}|\psi|^4+(\tilde{B}-\tilde{H})^2\,\right]</math> | |||
As shown in the figures below, type-I superconductor (left) has positive wall energy while type-II superconductor (right) negative wall energy. | |||
[[Image:pic4.jpg]] [[Image:pic3.jpg]] | |||
=== Free Energy of a Normal-Superconducting Interface === | |||
Now let's consider the free energy of a normal-superconducting interface. Recall the GL equations: | |||
<math>(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})^2\psi - \psi + \psi|\psi|^2 = 0</math> | |||
<math>\frac{1}{2}(\psi^*\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}\psi + c.c.)-\tilde{A}|\psi|^4 | |||
=\tilde{\nabla}\times(\tilde{\nabla}\times\tilde{A})</math> | |||
Assume that the interface is along y-z plane and <math>\tilde{B}\|\hat{z}</math>. We can choose <math>\tilde{A}(\tilde{r})=\hat{y}\tilde{A}(\tilde{x})</math> which implies the order parameter depends only on <math>\tilde{x}</math>. Then the GL equation become | |||
[[Image:pic5.jpg|right]] | |||
<math>-\frac{1}{\kappa^2}\frac{d^2\psi}{d\tilde{x}^2}+\tilde{A}_y^2(\tilde{x})\psi -\psi + \psi^3 = 0</math>(*) | |||
<math>\tilde{A}_y(\tilde{x})\psi^2 = \frac{d^2\tilde{A}_y(\tilde{x})}{d\tilde{x}^2}</math> | |||
and | |||
<math>\frac{1}{2}(\psi^*\frac{1}{\kappa}\frac{1}{i}\frac{d}{d\tilde{x}}\psi + c.c.) = 0</math> | |||
Note that we can choose <math>\psi</math> to be real since the coefficients are real. Now let's manipulate Eq.(*): | |||
<math>-\frac{1}{\kappa^2}\frac{d\psi}{d\tilde{x}}\frac{d^2\psi}{d\tilde{x}^2}+\tilde{A}_y^2\frac{d\psi}{d\tilde{x}}\psi | |||
- \frac{d\psi}{d\tilde{x}}\psi + \frac{d\psi}{d\tilde{x}}\psi^3 = 0</math> | |||
<math>-\frac{1}{2\kappa^2}\frac{d}{d\tilde{x}}(\frac{d\psi}{d\tilde{x}})^2+\frac{1}{2}\tilde{A}_y^2\frac{d}{d\tilde{x}}\psi^2 - \frac{1}{2}\frac{d}{d\tilde{x}}\psi^2 + \frac{1}{4}\frac{d}{\tilde{x}}\psi^4 = 0</math> | |||
Integrating we have | |||
<math>-\frac{1}{2\kappa^2}(\frac{d\psi}{d\tilde{x}})^2 + \frac{1}{2}\int d\tilde{x}\tilde{A}_y^2\frac{d}{d\tilde{x}}\psi^2 | |||
- \frac{1}{2}\psi^2 + \frac{1}{4}\psi^4 = const.</math> | |||
This integral can be further manipulated: | |||
<math>\int d\tilde{x}\tilde{A}_y^2\frac{d}{d\tilde{x}}\psi^2 = \int d\tilde{x}\,\left[\frac{d}{d\tilde{x}}(\tilde{A}_y^2\psi^2)-\frac{d\tilde{A}_y^2}{d\tilde{x}}\psi^2\,\right] | |||
= \tilde{A}_y^2\psi^2 - 2\int d\tilde{x}\tilde{A}_y\frac{d\tilde{A}_y}{d\tilde{x}}\psi^2 | |||
= \tilde{A}_y^2\psi^2 - 2\int d\tilde{x}\frac{d\tilde{A}_y}{d\tilde{x}}\frac{d^2\tilde{A}_y}{d\tilde{x}^2} | |||
= \tilde{A}_y^2\psi^2 - \int d\tilde{x}\frac{d}{d\tilde{x}}(\frac{d\tilde{A}_y}{d\tilde{x}})^2 | |||
= \tilde{A}_y^2\psi^2 - (\frac{d\tilde{A}_y}{d\tilde{x}})^2 = const.</math> | |||
Thus, Eq.(*) becomes | |||
<math>-\frac{1}{2\kappa^2}(\frac{d\psi}{d\tilde{x}})^2+\frac{1}{2}\tilde{A}_y^2\psi^2-\frac{1}{2}(\frac{d\tilde{A}_y}{d\tilde{x}})^2 - \frac{1}{2}\psi^2 + \frac{1}{4}\psi^4 = const.</math> | |||
or, | |||
<math>\frac{1}{\kappa^2}(\frac{d\psi}{d\tilde{x}})^2+(\frac{d\tilde{A}_y}{d\tilde{x}})^2+\psi^2(1-\tilde{A}_y^2)-\frac{1}{2}\psi^4 = const.</math> | |||
To determine the const., note that as <math>x\rightarrow -\infty</math>, <math>\psi \rightarrow 1</math> and <math>\tilde{A}_y \rightarrow 0</math>, so | |||
<math>0 + 0 + 1 - \frac{1}{2} = const.</math> | |||
Therefore, | |||
<math>\frac{1}{\kappa^2}(\frac{d\psi}{d\tilde{x}})^2+(\frac{d\tilde{A}_y}{d\tilde{x}})^2+\psi^2(1-\tilde{A}_y^2)-\frac{1}{2}\psi^4 = \frac{1}{2}</math> | |||
Consider the case where <math>\kappa << 1</math>, that is, <math>\lambda << \xi</math>. The main contribution to the surface energy comes from the region where <math>\tilde{B}=0</math> but <math>\psi < 1</math>. | |||
<math>\frac{1}{\kappa^2}(\frac{d\psi}{d\tilde{x}})^2+\psi^2-\frac{1}{2}\psi^4=\frac{1}{2}</math> | |||
<math>\frac{1}{\kappa^2}(\frac{d\psi}{d\tilde{x}})^2 = \frac{1}{2}-\psi^2+\frac{1}{2}\psi^4 = \frac{1}{2}(1-\psi^2)^2</math> | |||
<math>\frac{1}{\kappa}\frac{d\psi}{d\tilde{x}}=-\frac{1}{\sqrt{2}}(1-\psi^2)</math> | |||
Note that the minus sign is from the experimental setup. Further, | |||
<math>\frac{d\psi}{1-\psi^2}=-\frac{\kappa}{\sqrt{2}}d\tilde{x};\frac{1}{1-\psi^2}=\frac{1}{2}(\frac{1}{1-\psi}+\frac{1}{1+\psi})</math> | |||
<math>ln\frac{1+\psi}{1-\psi}=-\sqrt{2}\kappa \tilde{x}+const.</math> | |||
<math>\frac{1+\psi(\tilde{x})}{1-\psi(\tilde{x})}=const.\times e^{-\sqrt{2}\kappa \tilde{x}}</math> | |||
[[Image:pic6.jpg|right]] | |||
Requiring <math>\psi=0</math> at <math>\tilde{x}=0</math> gives <math>const.=1</math> Now we have | |||
<math>\psi = \frac{e^{-\sqrt{2}\kappa \tilde{x}}-1}{e^{-\sqrt{2}\kappa \tilde{x}}+1}=-tanh\frac{\kappa \tilde{x}}{\sqrt{2}}</math> | |||
whose curve is shown in the figure. Moreover, | |||
<math>F_s-F_n=\frac{H_c^2}{8\pi}L^2\lambda\int_{-\infty}^{0}d\tilde{x}(1-\psi^4)</math> | |||
where | |||
<math>\int_{-\infty}^{0}d\tilde{x}(1-\psi^4)=\int_{-\infty}^{0}d\tilde{x}(1+\psi^2)(1-\psi^2) | |||
=\int_{-\infty}^{0}d\tilde{x}(1+\psi^2)(-\frac{\sqrt{2}}{\kappa})\frac{d\psi}{d\tilde{x}} | |||
=-\frac{\sqrt{2}}{\kappa}\psi |_{-\infty}^{0}-\frac{\sqrt{2}}{\kappa}\int_{-\infty}^{0}d\tilde{x}\psi^2\frac{d\psi}{d\tilde{x}}</math> | |||
[[Image:pic7.jpg|right]] | |||
<math>=-\frac{\sqrt{2}}{\kappa}\psi |_{-\infty}^{0}-\frac{\sqrt{2}}{3\kappa}\int_{-\infty}^{0}d\tilde{x}\frac{d\psi^3}{d\tilde{x}} = -\frac{\sqrt{2}}{\kappa}\psi |_{-\infty}^{0}-\frac{\sqrt{2}}{3\kappa}\psi^3 |_{-\infty}^{0} = | |||
\frac{\sqrt{2}}{\kappa}+\frac{\sqrt{2}}{3\kappa} = \frac{4\sqrt{2}}{3\kappa}</math> | |||
Hence one has | |||
<math>F_s-F_n=\frac{H_c^2}{8\pi}L^2\lambda\cdot\frac{4\sqrt{2}}{3\kappa}</math> | |||
Below we show that given <math>\psi</math> and <math>\tilde{A}_y</math> satisfying the GL equation, the surface energy of the surface vanishes at <math>\kappa=1/2</math>: | |||
<math>\frac{1}{\kappa^2}(\frac{d\psi}{d\tilde{x}})^2+(\frac{d\tilde{A}_y}{d\tilde{x}})^2+\psi^2(1-\tilde{A}_y^2)-\frac{1}{2}\psi^4 = \frac{1}{2}</math>(**) | |||
<math>F_s-F_n=\frac{H_c^2}{4\pi}L^2\lambda\int d\tilde{x}\,\left[(\tilde{B}-\tilde{H})^2-\frac{1}{2}\psi^4\,\right]</math> | |||
Assume <math>\kappa=1/\sqrt{2}</math>. | |||
<math>F_s-F_n=\frac{H_c^2}{4\pi}L^2\lambda\int d\tilde{x}\,\left[(\frac{d\tilde{A}_y}{d\tilde{x}}-\frac{1}{\sqrt{2}})^2-\frac{1}{2}\psi^4\,\right]</math> | |||
Choosing | |||
<math>\frac{d\tilde{A}_y}{d\tilde{x}}=\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}\psi^2</math> | |||
then <math>F_s-F_n=0</math> and the 2nd GL equation becomes | |||
<math>\tilde{A}_y\psi^2=\frac{d^2\tilde{A}_y}{d\tilde{x}^2}=\frac{d}{d\tilde{x}}(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}\psi^2)=-\sqrt{2}\psi\frac{d\psi}{d\tilde{x}}</math> | |||
<math>\frac{d\psi}{d\tilde{x}}=-\frac{1}{\sqrt{2}}\tilde{A}_y\psi</math> | |||
Insert this into Eq.(**): | |||
<math>\frac{1}{\kappa^2}\frac{1}{2}\tilde{A}_y^2\psi^2+(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}\psi^2)^2+\psi^2(1-\tilde{A}_y^2)-\frac{1}{2}\psi^4-\frac{1}{2}=0</math> | |||
<math>\frac{1}{2\kappa^2}\tilde{A}_y^2\psi^2+\frac{1}{2}-\psi^2+\frac{1}{2}\psi^4+\psi^2-\tilde{A}_y^2\psi^2-\frac{1}{2}\psi^4-\frac{1}{2}=0</math> | |||
<math>(\frac{1}{2\kappa^2}-1)\tilde{A}_y^2\psi^2=0</math> | |||
Therefore, <math>\kappa=1/\sqrt{2}</math> as expected. | |||
In summary, for type-I superconductor (positive surface energy) <math>\kappa < 1/\sqrt{2}</math> and <math>\psi</math> is uniform in the bulk and jumps at <math>T_c</math>. On the other hand, for type-II superconductor (negative surface energy) <math>\kappa > 1/\sqrt{2}</math> and <math>\psi</math> is not uniform in the bulk but grows continuously when crossing <math>T_c</math> from above. | |||
=== The "Landau-Level"-Like States above Hc and the Upper Critical Field Hc2 === | |||
Now we have the surface free energy: | |||
<math>F_s-F_n=\frac{H_c^2}{4\pi}\lambda^3\int d^3\tilde{r} \,\left[-|\psi|^2+|(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})^2\psi|^2+\frac{1}{2}|\psi|^4+(\tilde{B}-\tilde{H})^2\,\right]</math> | |||
where | |||
<math>\tilde{B}=\frac{B}{\sqrt{2}H_c}</math> and <math>\tilde{A}=\frac{A}{\sqrt{2}\lambda H_c}</math> | |||
Assuming 2nd order phase transition and <math>T=T_c</math>, then <math>\psi\rightarrow 0</math> and <math>\tilde{B}\rightarrow\tilde{H}</math>: | |||
<math>F_s-F_n=\frac{H_c^2}{4\pi}\lambda^3\int d^3\tilde{r} \,\left[-|\psi|^2+|(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})^2\psi|^2\,\right]</math> | |||
Using the Landau gauge: | |||
<math>\vec{A}=\hat{y}Hx=\hat{y}\frac{H}{\sqrt{2}H_c}\frac{x}{\lambda}=\hat{y}\tilde{H}\tilde{x}</math> | |||
Recall | |||
<math>(\frac{1}{\kappa}\frac{\tilde{\nabla}}{i}-\tilde{A})^2\psi-\psi=0</math> | |||
<math>(\frac{1}{\kappa}\frac{1}{i}\frac{d}{d\tilde{x}})^2\psi+(\frac{1}{\kappa}\frac{1}{i}\frac{d}{d\tilde{y}}-\tilde{H}\tilde{x})^2\psi+(\frac{1}{\kappa}\frac{1}{i}\frac{d}{d\tilde{z}})^2\psi-\psi=0</math> | |||
<math>-\frac{1}{\kappa^2}\frac{d^2}{d\tilde{x}^2}\psi+(\frac{1}{\kappa}\frac{1}{i}\frac{d}{d\tilde{y}}-\tilde{H}\tilde{x})^2\psi-\frac{1}{\kappa^2}\frac{d^2}{d\tilde{z}^2}\psi-\psi=0</math> | |||
Let | |||
<math>\psi(\tilde{x},\tilde{y},\tilde{z})=e^{ik_z\tilde{z}}e^{ik\tilde{y}}\Phi_k(\tilde{x})</math> | |||
then | |||
<math>e^{ik_z\tilde{z}}e^{ik\tilde{y}}\,\left[-\frac{1}{\kappa^2}\frac{d^2}{d\tilde{x}^2}\Phi+(\frac{k}{\kappa}-\tilde{H}\tilde{x})^2\Phi+\frac{k_z^2}{\kappa^2}\Phi-\Phi\,\right]=0</math> | |||
Let | |||
<math>-\tilde{H}X=\frac{k}{\kappa}-\tilde{H}\tilde{x};\frac{d}{d\tilde{x}}=\frac{dX}{d\tilde{x}}\frac{d}{dX}=\frac{d}{dX}</math> | |||
then | |||
<math>e^{ik_z\tilde{z}}e^{ik\tilde{y}}(-\frac{1}{\kappa^2}\frac{d^2}{dX^2}+\tilde{H}^2 X^2+\frac{k_z^2}{\kappa^2}-1)\Phi=0</math> | |||
Recall for a harmonic oscillator we have | |||
<math>(\frac{-\hbar^2}{2m}\frac{d^2}{dx^2}+\frac{1}{2}m\omega^2 x^2)\Psi=E\Psi</math> | |||
and | |||
<math>E=\hbar\omega(n+\frac{1}{2})</math> | |||
Comparison leads to | |||
<math>\frac{-\hbar^2}{2m}\rightarrow\frac{-1}{\kappa^2};\frac{1}{2}m\omega^2\rightarrow\tilde{H}^2;\hbar\omega\rightarrow\frac{2\tilde{H}}{\kappa}</math> | |||
and the eigenvalues | |||
<math>2\frac{\tilde{H}}{\kappa}(n+\frac{1}{2})+\frac{k_z}{\kappa}-1</math> | |||
The exponent is zero when | |||
<math>2\frac{\tilde{H}}{\kappa}(n+\frac{1}{2})+\frac{k_z}{\kappa}-1=0</math> | |||
If <math>n=0</math> and <math>k_x=0</math> we have | |||
<math>\tilde{H}_{c2}=\kappa=\frac{H_{c2}}{\sqrt{2}H_c}</math> | |||
<math>H_{c2}=\sqrt{2}\kappa H_c</math> | |||
For <math>\kappa < 1/\sqrt{2}</math>, <math>H_{c2}<H_c</math>, the bulk is preempted by the Meissner phase. On the other hand, <math>\kappa > 1/\sqrt{2}</math>, <math>H_{c2}>H_c</math>, the bulk undergoes a 2nd order phase transition into a mixed state in which normal state and superconducting state coexist. | |||
Now let's look at the wavefunction at <math>H_{c2}</math>. | |||
<math>(-\frac{1}{\kappa^2}\frac{d^2}{dX^2}+\tilde{H}_{c2}^2 X^2)\Phi=\lambda\Phi;\tilde{H}_{c2}=\kappa</math> | |||
<math>(-\frac{1}{\kappa^2}\frac{d^2}{dX^2}+\kappa^2 X^2)\Phi=\lambda\Phi</math> | |||
Let | |||
<math>\frac{1}{\sqrt{2}}\frac{1}{\kappa}\frac{d}{dX}+\frac{1}{\sqrt{2}}\kappa X = a</math> | |||
<math>\frac{-1}{\sqrt{2}}\frac{1}{\kappa}\frac{d}{dX}+\frac{1}{\sqrt{2}}\kappa X = a^+</math> | |||
where <math>[a,a^{+}]=1</math> Note that | |||
<math>a^+ a=\frac{-1}{2\kappa^2}\frac{d^2}{dX^2}+\frac{1}{2}\kappa^2 X^2-\frac{1}{2}</math> | |||
<math>(2a^+ a+1)\Phi=\lambda\Phi</math> | |||
For <math>\lambda=1</math> we have | |||
<math>\frac{1}{\sqrt{2}}(\frac{1}{\kappa}\frac{d}{dX}+\kappa K)\Phi=0</math> | |||
<math>\Phi=const.\times e^{-\frac{1}{2}\kappa^2 X^2}</math> | |||
and the order parameter is of the form | |||
<math>const.\times e^{ik\tilde{y}}e^{-\frac{\kappa^2}{2}(\tilde{x}-\frac{k}{\kappa^2})^2}</math> | |||
=== Abrikosov Solution of the GL Equation for Type-II Superconductor near Hc2 === | |||
Note. In this section we will drop the "tilde(~)" on relevant quantities and recover it when necessary. | |||
Since the conditions along the entire superconductor are uniform, we seek a linear combination of solutions centered through equal intervals, namely, | |||
<math>\psi^{(0)}=\Sigma_{n=-\infty}^{\infty}C_n e^{ikn\hat{y}} e^{-\frac{1}{2}\kappa^2(x-\frac{kn}{\kappa^2})^2}</math> | |||
or, | |||
<math>\psi=\Sigma_{n=-\infty}^{\infty}C_n e^{ikny}\phi_n(x)</math> | |||
with | |||
<math>\phi_n(x)=e^{-\frac{1}{2}\kappa^2(x-\frac{kn}{\kappa^2})^2}</math> | |||
Consider the solution to GL equation at <math>H</math> slightly less than <math>\kappa</math>.The 2nd GL equation gives | |||
<math>\nabla\times(\nabla\times A^{(1)})=\frac{-i}{2\kappa}(\psi^{(0)*} \nabla\psi^{(0)}-\psi^{(0)}\nabla\psi^{(0)*})-|\psi^{(0)}|^2 A^{(0)}</math> | |||
<math>\nabla\times B=\hat{x}\frac{\partial B_z}{\partial y}-\hat{y}\frac{\partial B_z}{\partial x}</math> | |||
<math>A=\hat{y}A_y(x,y);\nabla\times A=\hat{z}\frac{\partial A}{\partial x}</math> | |||
For the x-component, we have | |||
<math>\frac{\partial B_z}{\partial y}=\frac{\partial^2 A_y}{\partial x\partial y}</math> | |||
<math>=\frac{-i}{2\kappa}\Sigma_{n=-\infty}^{\infty}\Sigma_{m=-\infty}^{\infty}C_n^* e^{-ikny}\phi_n(x)(\frac{\partial}{\partial x}\phi_m(x))C_me^{ikmy} | |||
+ \frac{i}{2\kappa}\Sigma_{n=-\infty}^{\infty}\Sigma_{m=-\infty}^{\infty}C_n^* e^{-ikny}(\frac{\partial}{\partial x}\phi_n(x))\phi_m(x)C_m e^{ikmy}</math> | |||
<math>=\frac{-i}{2\kappa}\Sigma_{n,m}C_n^* C_m e^{-ik(n-m)y}\,\left[\phi_n(x)\frac{\partial}{\partial x}\phi_m(x)-\phi_m(x)\frac{\partial}{\partial x}\phi_n(x)\,\right]</math> | |||
where | |||
<math>[...]=-\kappa^2(x-\frac{km}{\kappa^2})\phi_n(x)\phi_m(x)+\kappa^2(x-\frac{kn}{\kappa^2})\phi_n(x)\phi_m(x) | |||
=k(m-n)\phi_n(x)\phi_m(x)</math> | |||
<math>\frac{\partial B_z}{\partial y}=\frac{-i}{2\kappa}\Sigma_{n,m}C_n^* C_m e^{-ik(n-my)}k(m-n)\phi_n(x)\phi_m(x) | |||
=\frac{\partial}{\partial y}\,\left[\frac{1}{2\kappa}\Sigma_{n,m}C_n^* C_m e^{-ik(n-m)y}\phi_n(x)\phi_m(y)\,\right] | |||
=\frac{\partial}{\partial y}\,\left[\frac{-1}{2\kappa}|\psi^{(0)}|^2\,\right]</math> | |||
Similarly, for the y-component we have | |||
<math>-\frac{\partial B_z}{\partial x}=\frac{-i}{2\kappa}\Sigma_{n,m}\,\left[C_n^* e^{-ikny}\phi_n(x)ikm e^{ikmy}\phi_m(x)C_m+C_n^* ikne^{-ikny}\phi_n(x)e^{ikmy}\phi_m C_m\,\right]-\kappa x|\psi^{(0)}|^2</math> | |||
<math>=\frac{1}{2\kappa}\Sigma_{n,m}\,\left[k(n+m)-2\kappa^2x\,\right]C_n^* C_me^{-ik(n-m)y}\phi_m(x)\phi_n(x)</math> | |||
Note that | |||
<math>\frac{\partial}{\partial x}\,\left[\phi_m(x)\phi_m(x)\,\right]=\,\left[-\kappa^2(x-\frac{km}{\kappa^2})-\kappa^2(x-\frac{kn}{\kappa^2})\,\right]\phi_m(x)\phi_n(x)=-\,\left[2\kappa^2x-k(m+n)\,\right]\phi_m(x)\phi_n(x)</math> | |||
Therefore, | |||
<math>-\frac{\partial B_z}{\partial x}=\frac{\partial}{\partial x}\,\left[\frac{1}{2\kappa}|\psi^{(0)}|^2\,\right]</math> | |||
Now we have | |||
<math>\frac{\partial B_z}{\partial y}=-\frac{\partial}{\partial y}\,\left[\frac{1}{2\kappa}|\psi^{(0)}|^2\,\right]</math> | |||
<math>\frac{\partial B_z}{\partial x}=-\frac{\partial}{\partial x}\,\left[\frac{1}{2\kappa}|\psi^{(0)}|^2\,\right]</math> | |||
or, | |||
<math>B_z(x,y)=f(x)-\frac{1}{2\kappa}|\psi^{(0)}|^2</math> | |||
<math>B_z(x,y)=g(y)-\frac{1}{2\kappa}|\psi^{(0)}|^2</math> | |||
which implies | |||
<math>B_z(x,y)=const.-\frac{1}{2\kappa}|\psi^{(0)}|^2</math> | |||
At points where <math>\psi^{(0)}=0</math>, <math>B_z(x,y)=H_z</math>. So | |||
<math>B_z(x,y)=H_z-\frac{1}{2\kappa}|\psi^{(0)}|^2</math> | |||
Note that the correction (the 2nd term) comes from induced current. Furthermore, | |||
<math>A_y=xH_z-\frac{1}{2\kappa}\int dx |\psi^{(0)}|^2</math> | |||
Now let's consider the 1st GL equation: | |||
<math>(\frac{1}{\kappa}\frac{\nabla}{i}-A)^2\psi-\psi+\psi|\psi|^2=0</math> | |||
which is solced by dropping the non-linear term and A and leads to Hc2. | |||
<math>(\frac{1}{\kappa}\frac{\nabla}{i}-A^{(0)}-A^{(1)})^2(\psi^{(0)}+\psi^{(1)})-(\psi^{(0)}+\psi^{(1)})+(\psi^{(0)}+\psi^{(1)})|\psi^{(0)}+\psi^{(1)}|^2=0</math> | |||
'''To 0th oeder:''' | |||
<math>(\frac{1}{\kappa}\frac{\nabla}{i}-A^{(0)})^2\psi^{(0)}-\psi^{(0)}=0</math> | |||
<math>A_y^{(0)}=\kappa x</math> | |||
<math>\psi^{(0)}=\Sigma_{n=-\infty}^{\infty}C_ne^{ikny}\phi_n(x)</math> | |||
'''To 1st order:''' | |||
<math>(\frac{1}{\kappa}\frac{\nabla}{i}-A^{(0)})^2\psi^{(1)}-(\frac{1}{\kappa}\frac{\nabla}{i}-A^{(0)})\cdot A^{(1)}\psi^{(0)}-A^{(1)}\cdot(\frac{1}{\kappa}\frac{\nabla}{i}-A^{(0)})\psi^{(0)}-\psi^{(1)}+\psi^{(0)}|\psi^{(0)}|^2=0</math> | |||
<math>A_y^{(1)}=(H-\kappa)x-\frac{1}{2\kappa}\int^{x}|\psi|^2</math> | |||
<math>\psi^{(1)}=\Sigma_{-\infty}^{\infty}e^{ikny}\psi_n^{(1)}(x)</math> | |||
[[1st term:]] | |||
<math>\,\left[\frac{-1}{\kappa^2}\frac{\partial^2}{\partial x^2}+(\frac{1}{\kappa}\frac{1}{i}\frac{\partial}{\partial y}-\kappa x)^2 \,\right] \Sigma_n e^{ikny} \psi_n^{(1)}(x)= \Sigma_n e^{ikny} \,\left[\frac{-1}{\kappa^2}\frac{\partial^2}{\partial x^2}+(\frac{kn}{\kappa}-\kappa x)^2\,\right]\psi_n^{(1)}(x)</math> | |||
[[2nd term:]] | |||
<math>-(\frac{1}{\kappa}\frac{1}{i}\frac{\partial}{\partial y}-\kappa x)\,\left[(H-\kappa)x-\frac{1}{2\kappa}\int^x |\psi^{(0)}|^2\,\right]\Sigma_n e^{ikny} \phi_n(x)</math> | |||
<math>=\Sigma_{n=-\infty}^{\infty}C_ne^{ikny}(-\frac{kn}{\kappa}+\kappa x)(H-\kappa)x\phi_n(x) | |||
+(\frac{1}{\kappa}\frac{1}{i}\frac{\partial}{\partial y}-\kappa x)\frac{1}{2\kappa}\int^x dx'\Sigma_{m,p}C_m^*C_pe^{-ikmy}e^{ikpy}\phi_m(x')\phi_p(x')\Sigma_nC_ne^{ikny}\phi_n(x)</math> | |||
<math>=\Sigma_{n=-\infty}^{\infty}C_ne^{ikmy}(-\frac{kn}{\kappa}+\kappa x)(H-\kappa)\phi_n(x)+\Sigma_{n,m,p}C_nC_m^*C_pe^{ik(n-m+p)y}(\frac{n-m+p}{\kappa}-\kappa x)\frac{1}{2\kappa}\phi_n(x)\int^x dx'\phi_m(x')\phi_p(x')</math> | |||
[[3rd term:]] | |||
<math>\Sigma_nC_ne^{ikny}(-\frac{kn}{\kappa}+\kappa x)(H-\kappa)x\phi_n(x)+\Sigma_{n,m,p}C_nC_m^*C_pe^{ik(n-m+p)y}(\frac{kn}{\kappa}-\kappa x)\frac{1}{2\kappa}\phi_n(x)\int^x dx'\phi_m(x')\phi_p(x')</math> | |||
[[4th term:]] | |||
<math>-\Sigma_ne^{ikny}\psi_n^{(1)}(x)</math> | |||
[[5th term:]] | |||
<math>\Sigma_{n,m,p}C_nC_m^*C_pe^{ik(n-m+p)y}\phi_n(x)\phi_m(x)\phi_p(x)</math> | |||
Add them up, we have | |||
<math>\Sigma_ne^{ikny}\,\left[\frac{-1}{\kappa^2}\frac{\partial^2}{\partial x^2}+(\frac{kn}{\kappa}-\kappa x)^2 + 1\,\right]\psi^{(1)}=\Sigma_ne^{ikny}C_n2x(H-\kappa)(\frac{kn}{\kappa}-\kappa x)\phi_n(x)-\Sigma_{n,m,p}e^{ik(n-m+p)y}C_nC_m^*C_p\,\left[(\frac{(2n-m+p)k}{\kappa}-2\kappa)\frac{1}{2\kappa}\phi_n(x)\int^xdx'\phi(x')\phi(x')+\phi_n(x)\phi_m(x)\phi_p(x)\,\right]</math> | |||
Multiplying the whole equation by <math>e^{-ikNy}</math> and integrating over the variable y leads to | |||
<math>\,\left[\frac{-1}{\kappa^2}\frac{\partial^2}{\partial x^2}+(\frac{kN}{\kappa}-\kappa)^2-1\,\right]\psi_N^{(1)}(x)=C_N2x(H-\kappa)(\frac{kx}{\kappa}-\kappa x)\phi_N(x)-\Sigma_{m,p}C_{N+m-p}C_m^*C_p\,\left[(\frac{k}{\kappa}(2N+2m-2p-m+p)-2\kappa x)\frac{1}{2\kappa}\phi_{N+m-p}(x)\int^xdx'\phi_m(x')\phi_p(x')+\phi_{N+m-p}(x)\phi_m(x)\phi_p(x)\,\right]</math> | |||
where | |||
<math>\phi_n(x)=e^{-\frac{1}{2}\kappa^2(x-\frac{kn}{\kappa^2})^2}</math> | |||
The above equation has this (inhomogeneous) form: | |||
<math>\hat{O}|\psi_N^{(1)}>=|\Phi></math> | |||
Consider the homogeneous version of this equation: | |||
<math>\hat{O}|\chi>=0</math> | |||
The only way for the inhomogeneous equation to have a solution is if | |||
<math><\chi|\Phi>=0</math> | |||
Thus we need | |||
<math>\,\left[\frac{-1}{\kappa^2}\frac{\partial^2}{\partial x^2}+(\frac{kN}{\kappa}-\kappa x)^2-1\,\right]\chi(x)=0</math> | |||
Let | |||
<math>\chi(x)=e^{-\frac{1}{2}\kappa^2(x-\frac{kN}{\kappa^2})^2}=\phi_N(x)</math> | |||
then the identity is satisfied. | |||
<math>0=C_N2(H-\kappa)\int_{-\infty}^{\infty}dxx(\frac{kN}{\kappa}-\kappa x)\phi_N^2(x)-\Sigma_{m,p}C_{N-p+m}C_m^*C_p | |||
\,\left[\int_{-\infty}^{\infty}dx\phi_N(x)(\frac{k}{2\kappa^2}(2N+m-p)-x)\phi_{N+m-p}(x)\int^xdx'\phi_m(x')\phi_p(x') | |||
+\int_{-\infty}^{\infty}dx\phi_N(x)\phi_{N+m-p}(x)\phi_m(x)\phi_p(x)\,\right]</math> | |||
<math>0=\frac{\sqrt{\pi}}{\kappa}(1-\frac{H}{\kappa})C_N-\Sigma_{m,p}C_{N-p+m}C_m^*C_p(1-\frac{1}{2\kappa^2})\int_{-\infty}^{\infty}dx\phi_N(x)\phi_{N+m-p}(x)\phi_m(x)\phi_p(x)</math> | |||
So, previously all of this work has shown us the | <math>0=\frac{\sqrt{\pi}}{\kappa}(1-\frac{H}{\kappa})C_N+\Sigma_{m,p}C_{N-p+m}C_m^*C_p(1-\frac{1}{2\kappa^2})\sqrt{\frac{\pi}{2}}\frac{1}{\kappa}e^{-\frac{k^2}{2\kappa^2}((m-p)^2+(N-p)^2)}</math> | ||
Now, multiply both sides by <math>C_N^*</math> and sum over N we have | |||
<math>0=(1-\frac{H}{\kappa})\Sigma_NC_N^*C_N+\frac{1}{\sqrt{2}}(\frac{1}{2\kappa^2}-1)\Sigma_{N,m,p}C_N^*C_{N-p+m}C_m^*C_pe^{-\frac{k^2}{2\kappa^2}((m-p)^2+(N-p)^2)}</math> | |||
Taking the spatial average results in | |||
<math>0=(1-\frac{H}{\kappa})<|\psi|^2>+(\frac{1}{2\kappa^2}-1)<|\psi|^4></math> | |||
<math>1=\frac{\frac{H}{\kappa}-1}{\frac{1}{2\kappa^2}-1}\frac{<|\psi|^2>}{<|\psi|^4>}</math> | |||
<math><B>=H-\frac{1}{2\kappa}<|\psi|^2>=H-\frac{1}{2\kappa}\frac{H-\kappa}{\frac{1}{2\kappa}-\kappa}\frac{<|\psi|^2>^2}{<|\psi|^4>}</math> | |||
<math><B>=H-\frac{\kappa -H}{2\kappa^2-1}\frac{1}{\beta_A}</math> | |||
or, recovering the "tilde(~)", | |||
<math><\tilde{B}>=\tilde{H}-\frac{\kappa -\tilde{H}}{2\kappa^2-1}\frac{1}{\beta_A}</math> | |||
where | |||
<math>\beta_A=\frac{<|\psi|^4>}{<|\psi|^2>^2}</math> | |||
is the famous Abrikosov parameter which does not depend on <math>\tilde{H}</math> or the normalization of <math>\psi</math>. It is easy to see that <math>\beta_A</math> is always greater than or equal to 1: | |||
<math>|\psi|^2=<|\psi|^2>+\delta |\psi|^2</math> | |||
<math><|\psi|^4>=<|\psi|^2>^2+2<|\psi|^2><\delta |\psi|^2>+<(\delta |\psi|^2)^2></math> | |||
Note that | |||
<math><\delta |\psi|^2>=0</math> | |||
Hence | |||
<math><|\psi|^4>=<|\psi|^2>^2+<(\delta |\psi|^2)^2>\ge <|\psi|^2>^2</math> | |||
<math>\beta_A=\frac{<|\psi|^4>}{<|\psi|^2>^2}\ge 1</math> | |||
The equality holds when <math>\psi=1</math>. | |||
Recall that the surface free energy is given by | |||
<math>F_s-F_n=\frac{H_c^2}{4\pi}\lambda^3\int d^3\tilde{r}\,\left[(\tilde{B}-\tilde{H})^2-\frac{1}{2}|\psi|^4\,\right]</math> | |||
In order to obtain the thermodynamic potential which when differentiated with respect to H gives B we need to subtract <math>\tilde{H}^2</math> (which came from the normal term) from the above expression: | |||
<math>\Omega=\frac{H_c^2}{4\pi}\lambda^3\int d^3\tilde{r}\,\left[(\tilde{B}-\tilde{H})^2-\tilde{H}^2-\frac{1}{2}|\psi|^4\,\right]</math> | |||
<math>=\frac{H_c^2}{4\pi}L^3\,\left[\frac{1}{4\kappa^2}<|\psi|^4>-\tilde{H}^2-\frac{1}{2}<|\psi|^4>\,\right]</math> | |||
<math>=\frac{H_c^2}{8\pi}L^3\,\left[\frac{1-2\kappa^2}{2\kappa^2}<|\psi|^4>-2\tilde{H}^2\,\right]</math> | |||
<math>=\frac{H_c^2}{8\pi}L^3\,\left[\frac{2}{1-2\kappa^2}\frac{1}{\beta_A}(\tilde{H}-\kappa)^2-2\tilde{H}^2\,\right]</math> | |||
Note that for type-II superconductor, <math>\kappa >1/\sqrt{2}</math>, the whole expression is negative. So, to lower the the free energy we need to minimize <math>\beta_A</math>. | |||
Knowing <math>\Omega</math> we can obtain <math>\tilde{B}</math> by differentiating <math>\Omega</math> with respect to <math>\tilde{H}</math> and hence obtain the magnetization which is measurable. | |||
<math>-\frac{4\pi}{L^3}\frac{\partial\Omega}{\partial H}=B</math> | |||
<math>\tilde{H}=\frac{H}{\sqrt{2}H_c};\frac{\partial}{\partial H}=\frac{\partial\tilde{H}}{\partial H}\frac{\partial}{\partial H}=\frac{1}{\sqrt{2}H_c}\frac{\partial}{\partial\tilde{H}}</math> | |||
<math>B=-\frac{H_c}{2\sqrt{2}}4(\frac{1}{\beta_A}\frac{\tilde{H}-\kappa}{1-2\kappa^2}-\tilde{H}) | |||
=-\frac{2H_c}{\sqrt{2}}\,\left[\frac{1}{\beta_A}\frac{1}{1-2\kappa^2}(\frac{H}{\sqrt{2}H_c}-\frac{H_{c2}}{\sqrt{2}H_c})-\frac{H}{\sqrt{2}H_c}\,\right]=\frac{1}{\beta_A}\frac{1}{1-2\kappa^2}(H-H_{c2})+H\le H</math> | |||
[[Image:pic8.jpg|right]] | |||
for <math>H<H_{c2}</math>. | |||
<math>B=H+4\pi M</math> | |||
<math>4\pi M=B-H=\frac{1}{\beta_A}\frac{1}{2\kappa^2-1}(H-H_{c2})<0</math> | |||
which means the type-II superconductor behaves like a diamagnet. | |||
=== Abrikosov Vortex States === | |||
Now let's follow the step of Abrikosov to derive the vortex structure in type-II superconductor. | |||
<math>\psi=\Sigma_{n=-\infty}^{\infty}C_ne^{ikny}e^{-\frac{1}{2}\kappa^2(x-\frac{kn}{\kappa^2})^2} | |||
=C\Sigma_{n=-\infty}^{\infty}e^{ikny}e^{-\frac{1}{2}\kappa^2(x-\frac{kn}{\kappa^2})^2}</math> | |||
where <math>C_n=C</math>. | |||
<math>|\psi|^2=|C|^2\Sigma_{m,n}e^{-ikny}e^{ikmy}e^{-\frac{1}{2}\kappa^2(\tilde{x}-\frac{kn}{\kappa^2})^2}e^{-\frac{1}{2}\kappa^2(\tilde{x}-\frac{km}{\kappa^2})^2}</math> | |||
<math>\int d\tilde{x}d\tilde{y}d\tilde{z}|\psi|^2=L_yL_z\Sigma_n\int d\tilde{x}|C|^2e^{-\kappa^2(\tilde{x}-\frac{kn}{\kappa^2})^2}=L_yL_z\frac{\kappa^2}{k}\tilde{L}_x\frac{\sqrt{\pi}}{\kappa}|C|^2</math> | |||
Thus | |||
<math><|\psi|^2>=|C|^2\frac{\sqrt{\pi}\kappa}{k}</math> | |||
<math>|\psi|^4=|C|^4\Sigma_{m,n}\Sigma_{s,t}e^{-ikmy}e^{ikny}e^{-iksy}e^{ikty}e^{-\frac{\kappa^2}{2}(x-\frac{km}{\kappa^2})^2}e^{-\frac{\kappa^2}{2}(x-\frac{kn}{\kappa^2})^2}e^{-\frac{\kappa^2}{2}(x-\frac{ks}{\kappa^2})^2}e^{-\frac{\kappa^2}{2}(x-\frac{kt}{\kappa^2})^2}</math> | |||
<math>\int dxdydz|\psi|^4=L_yL_z|C|^4\Sigma_{m,n,s}\int dx e^{-\frac{\kappa^2}{2}(x-\frac{km}{\kappa^2})^2}e^{-\frac{\kappa^2}{2}(x-\frac{kn}{\kappa^2})^2}e^{-\frac{\kappa^2}{2}(x-\frac{ks}{\kappa^2})^2}e^{-\frac{\kappa^2}{2}(x-\frac{k(m-n+s)}{\kappa^2})^2}</math> | |||
<math>=L_yL_z|C|^4\Sigma_{m,n,s}\sqrt{\frac{\pi}{2}}\frac{1}{\kappa}e^{-\frac{k^2}{2\kappa^2}((m-n)^2+(n-s)^2)}</math> | |||
<math>=L_yL_z|C|^4\sqrt{\frac{\pi}{2}}\frac{1}{k}\frac{\kappa^2}{k}\tilde{L}_x\Sigma_{m,n}e^{-\frac{k^2}{2\kappa^2}(m^2+n^2)}</math> | |||
<math>\beta_A=\frac{1}{\sqrt{2\pi}}\frac{k}{\kappa}(\Sigma_{n=-\infty}^{\infty}e^{-\frac{k^2n^2}{2\kappa^2}})^2</math> | |||
Minimize <math>\beta_A</math> with respect to k we find that at minimum | |||
<math>k=\sqrt{2\pi}\kappa</math> | |||
<math>\psi=C\Sigma_{n=-\infty}^{\infty}e^{i\sqrt{2}\pi n\kappa\tilde{y}}e^{-\frac{1}{2}(\kappa\tilde{x}-\sqrt{2}\pi n)^2}</math> | |||
where <math>\beta_A=1.18034</math> and | |||
<math>\psi=Ce^{-\frac{1}{2}\kappa^2\tilde{x}^2}\Sigma_{n=-\infty}^{\infty}e^{i\sqrt{2\pi}n\kappa\tilde{y}}e^{\sqrt{2\pi}n\kappa\tilde{x}}e^{-\pi n^2}=Ce^{-\frac{1}{2}\kappa^2\tilde{x}^2}\Sigma_{n=-\infty}^{\infty}e^{\sqrt{2\pi}\kappa (\tilde{x}+i\tilde{y})n}e^{-\pi n^2}=Ce^{-\frac{1}{2}\kappa^2\tilde{x}^2}\theta_3 (\sqrt{\frac{\pi}{2}}\kappa (\tilde{y}-i\tilde{x}),e^{-\pi})</math> | |||
where <math>\theta_3</math> is the Jacobi elliptic theta function. The <math>\psi</math> vanishes at points: | |||
<math>\tilde{y}=\sqrt{\frac{\pi}{2}}\frac{1}{\kappa}(2m-1)</math> | |||
and | |||
<math>\tilde{x}=\sqrt{\frac{\pi}{2}}\frac{1}{\kappa}(1-2n)\rightarrow\sqrt{\frac{\pi}{2}}\frac{1}{\kappa}(2n-1)</math> | |||
Obviously, the zeros form a square lattice of spacing <math>\frac{\sqrt{2\pi}}{\kappa}</math> in reduced units. | |||
Now consider the current lines: | |||
<math>\vec{j}=\frac{-i}{2\kappa}(\psi^*\nabla\psi-\psi\nabla\psi^*)-|\psi|^2\tilde{A}</math> | |||
<math>j_x=\frac{1}{2\kappa i}\Sigma_{m,n}k(n-m)C_m^*C_ne^{-ik(m-n)\tilde{y}}\phi_n(\tilde{x})\phi_m(\tilde{x})=\frac{-1}{2\kappa}\frac{\partial}{\partial\tilde{y}}|\psi|^2</math> | |||
<math>j_y=\frac{1}{2\kappa}\frac{\partial}{\partial\tilde{x}}|\psi|^2</math> | |||
The lines of constant current magnitude are determined by the following condition: | |||
[[Image:pic9.jpg|right]] | |||
<math>\frac{dy}{dx}=\frac{j_y}{j_x}</math> | |||
<math>j_xdy-j_ydx=0</math> | |||
<math>\frac{-1}{2\kappa}(\frac{\partial}{\partial y}|\psi|^2)dy-\frac{1}{2\kappa}(\frac{\partial}{\partial x}|\psi|^2)dx=0</math> | |||
<math>d|\psi|^2=0</math> | |||
<math>|\psi|^2=const.</math> | |||
which means the current flows along the contours of <math>|\psi|^2</math>. | |||
However, the actual solution which minimizes <math>\beta_A</math> is a triangular lattice for which the coefficients satisfy | |||
<math>C_{n+4}=C_n;C_0=C_1=C;C_2=C_3=-C</math> | |||
and <math>\beta_A=1.16</math>. | |||
==Going below Tc with the Saddle Point Approximation== | |||
So, previously all of this work has shown us the behaviour of a superconducting system near <math>T_c</math> only. If we want to go into lower temperatures, we will have to make a careful saddle-point approximation, following Bardeen, Cooper, and Schrieffer (BCS). Once again, we can start from our [[#Pairing Hamiltonian and BCS instability|microscopic 'toy' Hamiltonian]], and gain useful information. | |||
Recall that the partition function can be written, | Recall that the partition function can be written, | ||
| Line 759: | Line 1,794: | ||
So that, from the saddle-point condition, we find the Self-Consistency Equation: | So that, from the saddle-point condition, we find the Self-Consistency Equation: | ||
<math> \frac{\Delta_{sp}(\vec{r},\tau)}{g} = \langle\psi_{\downarrow}(\vec{r},\tau) \psi_{\uparrow}(\vec{r},\tau)\rangle_{BCS} </math> | <math>{ \frac{\Delta_{sp}(\vec{r},\tau)}{g}} = {\langle\psi_{\downarrow}(\vec{r},\tau) \psi_{\uparrow}(\vec{r},\tau)\rangle_{BCS}} </math> | ||
This contains the same information as the Ginzburg-Landau equations, but also more, as we can now go far below <math>T_c</math>. Evaluation of this cam be done formally, but is difficult and not terribly enlightening. Instead, we will search for a solution in which <math\psi</math> is independent of <math>\vec{r}</math> and <math>\tau</math>, similar to our solution near <math>T_c<math>. In this case, we also expect that <math>\Delta</math> will be independent of <math>\vec{r}</math> and <math>\tau</math>. | This contains the same information as the Ginzburg-Landau equations, but also more, as we can now go far below <math>T_c</math>. Evaluation of this cam be done formally, but is difficult and not terribly enlightening. Instead, we will search for a solution in which <math\psi</math> is independent of <math>\vec{r}</math> and <math>\tau</math>, similar to our solution near <math>T_c</math>. In this case, we also expect that <math>\Delta</math> will be independent of <math>\vec{r}</math> and <math>\tau</math>. | ||
First, it is useful to write down the action in momentum and frequency space, before evaluating the correlator. | First, it is useful to write down the action in momentum and frequency space, before evaluating the correlator. | ||
| Line 840: | Line 1,875: | ||
Note that this is only possible if <math> g < 0 </math>! | Note that this is only possible if <math> g < 0 </math>! | ||
-We will not get S-wave superconductivity for <math>\Delta</math> independent of <math>k</math> | |||
-In cuprates, <math>\Delta(k)</math> changes sign with <math>90^{0}</math>. It changes sign like D-wave. | |||
-If <math>g</math> is repulsive system does not like to make uniform gap! | |||
-In Fe-Pnictides, pairing gaps on different Fermi surfaces have different signs, with repulsion. | |||
Let us define | |||
<math>E_{k}^{2} = (\epsilon_{k} - \mu)^{2} + |\Delta|^{2} </math> | |||
So | |||
<math>\frac{-1}{g} = \frac{1}{\beta}\sum_{\omega_n}\frac{1}{V}\sum_{\vec{k}}\frac{1}{-\omega_n^2 - (\epsilon_{\vec{k}} - \mu)^2 - |\Delta|^2 } </math> | |||
<math>\frac{-1}{g} = \frac{1}{\beta}\sum_{\omega_n}\sum_{\vec{k}}\frac{1}{-\omega_n^2 - E_{\vec{k}}^{2} } </math> | |||
<math>= \frac{1}{\beta}\sum_{\omega_{n}}\frac{1}{(i\omega_{n} - E_{\vec{k}})(i\omega_{n} + E_{\vec{k}})}</math> | |||
<math>\omega_{n} = \frac{(2n + 1)\pi}{\beta}</math> | |||
We can write this as a complex contour integral, with a series of pole along the imaginary axis. | |||
<math>\frac{-1}{g} = \oint_{c} \frac{dz}{2\pi i}\frac{1}{e^{\beta z} + 1}f(z)</math> | |||
since | |||
<math> \frac{1}{e^{\beta(\frac{\pi}{\beta}i + \delta z)} + 1} = \frac{1}{-e^{\beta \delta z +1}} = \frac{-1}{\beta\delta z}</math> | |||
<math>\frac{-1}{g}= \oint_{c}\frac{dz}{(2\pi i)}\frac{1}{e^{\beta z} + 1}\frac{1}{(z-E_{\vec{k}})(z+E_{\vec{k}})}</math> | |||
There is no divergence as <math>z \to i\infty</math> | |||
There are two poles, at <math>Z = \pm E_{\vec{k}}</math> | |||
The contour can be deformed so that they exclude these two poles, and the integrand is tiny as <math>Re(z) \to \infty</math> | |||
The only contribution comes from the the loop around the two poles. For <math>Re(z)\to -\infty</math>, the integrand falls off as <math>\frac{1}{z^{2}}</math> , which, by Jordan's lemma,is fast enough for convergence. | |||
So the integrand becomes | |||
<math> = \frac{-1}{2\pi i}2\pi i \left [\frac{1}{(e^{\beta E_{\vec{k}}} +1)}\frac{1}{2E_{\vec{k}}} + \frac{1}{(e^{\beta E_{\vec{k}}}+1)}\frac{1}{-2E_{\vec{k}}} \right ]</math> | |||
<math>= \frac{1}{2E_{\vec{k}}}\left [ \frac{1}{(e^{-\beta E_{\vec{k}}} +1)} - \frac{1}{(e^{\beta E_{\vec{k}}} +1)}\right ]</math> | |||
<math>=\frac{1}{2E_{\vec{k}}}\left [ \frac{1}{e^{-\beta E_{\vec{k}}/2}2\cosh(\beta E_{\vec{k}}/2)} - \frac{1}{e^{\beta E_{\vec{k}}/2}2\cosh(\beta E_{\vec{k}}/2)}\right ]</math> | |||
<math>= \frac{1}{4E_{\vec{k}}\cosh(\beta E_{\vec{k}}/2)}\left [ e^{\beta E_{\vec{k}}/2}2 - e^{-\beta E_{\vec{k}}/2}2 \right ]</math> | |||
<math>= \frac{1}{2E_{\vec{k}}}\tanh(\beta E_{\vec{k}}/2)</math> | |||
<math>\Rightarrow \frac{1}{g} = \frac{-1}{V}\sum_{\vec{k}}\frac{1}{2E_{\vec{k}}}\tanh(E_{\vec{k}}/2k_{b}T)</math> | |||
===Solution of the Self-Consistency Equation=== | |||
By using our usual trick of <math>\sum_{\vec{k}} \to V\int \frac{d^{3}k}{(2\pi)^3}</math>, | |||
we can convert the sum into an integral: | |||
<math>\frac{1}{|g|} = -\frac{1}{g} = \int \frac{d^{3}k}{(2\pi)^3}\frac{\tanh(E_{\vec{k}}/2k_{b}T)}{2E_{\vec{k}}}</math> | |||
At this point, we can, if we wish, solve this equation on a computer, at any temperature | |||
For <math>\Delta \to 0</math>, the RHS is <math>\frac{\tanh((\epsilon_{\vec{k}}-\mu)/2k_{b}T)}{(\epsilon_{\vec{k}}-\mu)}</math> always intersects the LHS <math>\left (\frac{1}{|g|} \right )</math>, and we are guaranteed a solution. | |||
As we raise temperature, log-divergence of integer gets cut-off. | |||
Finding T-dependence of the intercept gives T-dependence of <math>\Delta</math> | |||
There can be an analytic solution as <math>T \to 0</math> | |||
<math>\frac{1}{|g|} = -\frac{1}{g} = \int \frac{d^{3}k}{(2\pi)^3}\frac{1}{2E_{\vec{k}}} = \int \frac{d^{3}k}{(2\pi)^3}\frac{1}{2\sqrt{(\epsilon_{\vec{k}} - \mu)^2 + |\Delta|^2}} </math> | |||
Assuming that the density of states is smooth, and dominated by <math>\xi \rightarrow 0 </math>, we can write: | |||
<math>\simeq N(\mu) \int_{-\hbar \omega_D}^{\hbar \omega_D}{d\xi}\frac{1}{2\sqrt{\xi^2 + |\Delta|^2}} = N(\mu) \int_0^{\frac{\hbar \omega_D}{|\Delta|}}{d\xi}\frac{1}{\sqrt{\xi^2 + |\Delta|^2}} </math> | |||
Now, | |||
<math> \frac{1}{|g|} = N(\mu) \ln{\left(\frac{\hbar \omega_D}{\Delta} + \sqrt{1 + \frac{\hbar^2\omega_d^2}{|\Delta|^2}}\right)} </math> | |||
In typical systems, <math>\Delta \ll \omega_D </math>! For example, in Al, <math>|\Delta| \simeq 2K</math> while <math> \omega_d \simeq 300-500K</math>. | |||
So, we can safely assume that <math> \frac{\hbar \omega_D}{|\Delta|} \gg 1 </math>, which gives that: | |||
<math>\frac{1}{|g|} = N(\mu) \ln{\left(\frac{h\hbar\omega_D} {\Delta} \right)} \Rightarrow |\Delta| = 2\hbar\omega_D e^{-\frac{1}{|g|N(\mu)}}</math> at <math> T = 0</math>. | |||
This actually lowers condensation energy more than <math>\Delta = 0</math>! It is also important to note, that since <math>|g|</math> enters in a exponential, that the <math>\Delta</math> is completely flat as <math>|g| \rightarrow 0</math>, showing that this result is completely non-perturbative. Note that <math>\Delta</math> is only exactly zero when <math>|g|</math> is zero, so that ''no matter how small the interaction'', we still have a superconducting state. | |||
[[Image:Deltavsg.jpeg]] | |||
Happily, this result is also something we can compare to experimental results from tunneling measurements on suitable materials (S-wave superconductors). From the definition of <math>T_c</math>: | |||
<math> \frac{|\Delta|(T = 0)}{k_B T_c} = \frac{2}{1.134} = 1.764 </math> | |||
By convention, the BCS results for twice this is compared to experiment. | |||
<math>\frac{2|\Delta|(T = 0)}{k_B T_c} = 3.53 </math> | |||
{|border="4" | |||
|Element || Measured <math>\frac{2\Delta(0)}{k_B T_c}</math> | |||
|- | |||
|Al ||<math>4.2\pm0.6</math> | |||
|- | |||
| ||<math>2.5 \pm0.3</math> | |||
|- | |||
| ||<math> 3.2\pm0.4 </math> | |||
|- | |||
|Cd ||<math>~3.2</math> | |||
|- | |||
|Nb ||<math>~3.84 </math> | |||
|- | |||
|Sn ||<math>3.49\pm0.1</math> | |||
|- | |||
| ||<math>3.1\pm0.05</math> | |||
|- | |||
| ||<math>3.5\pm0.18</math> | |||
|- | |||
|} | |||
====Going between <math>T = 0</math> and <math>T_c</math>==== | |||
At zero-Temperature, | |||
<math>\Delta = 2\hbar\omega_{D}e^{\frac{1}{gN_{0}}}</math> | |||
Now lets look at how it agrees with the Ginzburg-Landau theory near <math>T_{c}</math> | |||
At finite T, | |||
<math>\frac{1}{g} = \int \frac{d^{3}k}{(2\pi)^3}\frac{\tanh(E_{\vec{k}}/2T)}{2E_{\vec{k}}}</math> | |||
in units of | |||
<math>E_{\vec{k}} = \left [ \epsilon^{2} + \Delta^2(T) \right ]^\frac{1}{2}</math> | |||
<math>\Rightarrow \frac{1}{g} = N_{\mu}\int^{\omega_{D}}_{0}d\epsilon \frac{\tanh\left( \frac{\left [ (\epsilon^{2} + \Delta^2(T) \right ]^\frac{1}{2}}{2T}\right)}{ \left [ \epsilon^{2} + \Delta^2(T) \right ]^\frac{1}{2}}</math> | |||
Now. let us parametrize <math>\Delta(T)</math> with <math>\Delta(T = 0)</math> | |||
(Note at | |||
<math>T =0, \frac{1}{g} = N_{\mu}\int^{\omega_{D}}_{0}d\epsilon \frac{1}{ \left [ \epsilon^{2} + \Delta^2 \right ]^\frac{1}{2}}</math>) | |||
so <math> N_{0}(\mu)\int_{0}^{\omega_{D}} d\epsilon \frac{1}{\sqrt{\epsilon^2 + \Delta^{2}(T=0)}}= N_{0}(\mu)\int_{0}^{\omega_{D}} d\epsilon \frac{tanh\left( \frac{\sqrt{(\epsilon^{2} + \Delta^2(T)}}{2T}\right)}{\sqrt{\epsilon^2 + \Delta^{2}(T)}}</math> | |||
Or,<math>\int_{0}^{\omega_{D}\to \infty} d\epsilon \left (\frac{1}{\sqrt{\epsilon^2 + \Delta^{2}(T=0)}} - \frac{1}{\sqrt{\epsilon^2 + \Delta^{2}(T)}}\right ) = \int_{0}^{\omega_{D\to \infty}} d\epsilon \left (\frac{\tanh\left( \frac{\sqrt{(\epsilon^{2} + \Delta^2(T)}}{2T}\right)-1}{\sqrt{\epsilon^2 + \Delta^{2}(T)}} \right )</math> | |||
Now <math>\omega_{D} \sim 1000-3000 K</math> , which is very large compared to the energy scale we are working at, and so we can replace the upper limit in the integrals by <math>\infty</math> . This will cause the first term in the LHS to vanish, since it falls faster than <math>\frac{1}{\epsilon^{2}}</math> | |||
We get, | |||
<math>\ln\left(\frac{\Delta(T)}{\Delta(0)}\right ) = \int_{0}^{\omega_{D\to \infty}} d\epsilon \left (\frac{\tanh\left( \frac{\sqrt{(\epsilon^{2} + \Delta^2(T)}}{2T}\right)-1}{\sqrt{\epsilon^2 + \Delta^{2}(T)}} \right )</math> | |||
Since we expect <math>\Delta(T)<\Delta(0)</math>, we can switch their order inside the logarithm: | |||
<math>\ln\left(\frac{\Delta(T=0)}{\Delta(T)}\right ) = \int_{0}^{\omega_{D\to \infty}} d\epsilon \left (\frac{1-\tanh\left( \frac{\sqrt{(\epsilon^{2} + \Delta^2(T)}}{2T}\right)}{\sqrt{\epsilon^2 + \Delta^{2}(T)}} \right )</math> | |||
We are now in a position to solve for <math>\Delta(T)</math> near <math>T = 0</math> | |||
Let <math>\epsilon/\Delta(T) = \xi</math> | |||
So the RHS is <math>\int_{0}^{\infty}d\xi \frac{1}{\sqrt{\xi^{2}+1}}\left(1-\tanh\left(\frac{\Delta(T)}{2T}\sqrt{\xi^{2}+1}\right)\right)</math> | |||
Let us call <math>\sqrt{\xi^{2}+1} = X</math>. So | |||
<math>\ln\left(\frac{\Delta(T=0)}{\Delta(T)}\right ) = \int_{1}^{\infty}dX \frac{1}{\sqrt{X^{2}-1}}\left(1-\tanh\left(\frac{\Delta(T)}{2T}X\right)\right)</math> | |||
<math>\rightarrow \ln\left(\frac{\Delta(T=0)}{\Delta(T)}\right ) = \int_{1}^{\infty}dX \frac{1}{\sqrt{X^{2}-1}}\frac{2}{e^{\frac{\Delta(T)X}{T}+1}}</math> | |||
Now as <math>T\to 0</math>, the integral clearly goes to zero | |||
So the integral is | |||
<math>2\int_{1}^{\infty}dX \frac{1}{\sqrt{X^{2}-1}}\frac{e^{-\frac{\Delta(T)X}{T}}}{e^{-\frac{\Delta(T)X}{T}}+1}</math> | |||
<math>= 2\int_{1}^{\infty}dX \frac{1}{\sqrt{X^{2}-1}}e^{-\frac{\Delta(T)X}{T}}\sum_{n=0}^{\infty}(-1)^n e^{-\frac{n\Delta(T)X}{T}}</math> | |||
<math>= 2\sum_{n=0}^{\infty}(-1)^n\int_{1}^{\infty}dX \frac{1}{\sqrt{X^{2}-1}} e^{-\frac{\Delta(T)X(n+1)}{T}}</math> | |||
<math>= 2\sum_{n=0}^{\infty}(-1)^n K_{0}\left({\frac{\Delta(T)X(n+1)}{T}}\right)</math> | |||
Where <math>K_{0}</math> is the modified Bessel function of the 2nd kind. | |||
As <math>x \to 0, K(x) \to \infty</math>, and as <math>x \to \infty, K(x) \to 0</math> | |||
For small temperatures, the sum is dominated by the smallest n value. So approximately, | |||
<math>\ln\left(\frac{\Delta(T=0)}{\Delta(T)}\right ) 2\simeq \sqrt{\frac{\pi T}{2\Delta(0)}}e^{-\frac{\Delta(0)}{T}}</math> | |||
By noting that <math>\Delta(T)-\Delta(0)</math> is small, we can manipulate the logarithm to get | |||
<math>-\ln\left(\frac{\Delta(T)-\Delta(0)+\Delta(0)}{\Delta(0)}\right )</math> | |||
<math>= -\ln\left(1 + \frac{\Delta(T)-\Delta(0)}{\Delta(0)}\right )</math> | |||
<math>\simeq -\frac{\Delta(T)-\Delta(0)}{\Delta(0)}</math> | |||
<math>\Rightarrow 1- \frac{\Delta(T)}{\Delta(0)} \simeq 2\sqrt{\frac{\pi T}{2\Delta(0)}}e^{-\frac{\Delta(0)}{T}}</math> | |||
<math>\Rightarrow \frac{\Delta(T)}{\Delta(0)} \simeq 1- 2\sqrt{\frac{\pi T}{2\Delta(0)}}e^{-\frac{\Delta(0)}{T}}</math> | |||
Next,let us solve near <math>T = T_{c}</math> analytically | |||
Near <math> T_{c}, \Delta(T) \to 0</math> | |||
<math>-\frac{1}{gN_{0}} = \int_{0}^{\omega_{D}} d\epsilon \frac{\tanh\left(\frac{\sqrt{(\epsilon^{2} + \Delta^2(T)}}{2T}\right)}{\sqrt{\epsilon^2 + \Delta^{2}(T)}}</math> | |||
At <math>T = T_{c}. \Delta = 0</math>. So, | |||
<math>-\frac{1}{gN_{0}} = \int_{0}^{\omega_{D}} d\epsilon \frac{\tanh\left( \frac{\epsilon}{2T_{c}}\right)}{\epsilon}</math> | |||
<math>\Rightarrow \int_{0}^{\omega_{D}} d\epsilon \frac{\tanh\left( \frac{\epsilon}{2T_{c}}\right)}{\epsilon} = \int_{0}^{\omega_{D}} d\epsilon \frac{\tanh\left(\frac{\sqrt{(\epsilon^{2} + \Delta^2(T)}}{2T}\right)}{\sqrt{\epsilon^2 + \Delta^{2}(T)}}</math> | |||
Let us subtract <math>\int_{0}^{\omega_{D}} d\epsilon \frac{\tanh\left( \frac{\epsilon}{2T}\right)}{\epsilon}</math> from both sides | |||
<math>\Rightarrow \int_{0}^{\omega_{D}} d\epsilon \frac{\tanh\left( \frac{\epsilon}{2T_{c}}\right)-\tanh\left( \frac{\epsilon}{2T_{c}}\right)}{\epsilon} = \int_{0}^{\omega_{D}} d\epsilon \left ( \frac{\tanh\left(\frac{\sqrt{(\epsilon^{2} + \Delta^2(T)}}{2T}\right)}{\sqrt{\epsilon^2 + \Delta^{2}(T)}} -\frac{\tanh\left( \frac{\epsilon}{2T}\right)}{\epsilon} \right ) </math> | |||
Now if we let <math>\omega_{D} \to \infty</math>, the reason of which has already been argued, we can solve the LHS exactly, and we get, | |||
<math>\ln \left (\frac{T}{T_{c}}\right)</math> | |||
So we get | |||
<math>\ln \left (\frac{T_{c}}{T}\right) = \int_{0}^{\infty} d\epsilon \left (\frac{\tanh\left( \frac{\epsilon}{2T}\right)}{\epsilon} -\frac{\tanh\left(\frac{\sqrt{(\epsilon^{2} + \Delta^2(T)}}{2T}\right)}{\sqrt{\epsilon^2 + \Delta^{2}(T)}}\right )</math> | |||
The next logical step is to expand the hyperbolic tangent | |||
<math>\tanh(\pi x/2) = \frac{4x}{\pi}\sum_{k = 0}^{\infty}\frac{1}{(2k+1)^2+x^2} </math> | |||
So RHS | |||
<math>=\int_{0}^{\infty} d\epsilon \left (\frac{4}{\pi^{2}T}\sum_{k = 0}^{\infty}\frac{1}{(2k+1)^2+\left ( \frac{\epsilon^2}{\pi^{2}T^{2}}\right)}-\frac{4}{\pi^{2}T}\sum_{k = 0}^{\infty}\frac{1}{(2k+1)^2+\left ( \frac{\epsilon^2}{\pi^{2}T^{2}}\right)} \right )</math> | |||
<math>=\sum_{k = 0}^{\infty}\int_{0}^{\infty} d\epsilon\frac{4}{\pi^{2}T}\frac{\frac{\Delta^2}{\pi^{2}T{2}}}{\left ((2k+1)^2+\left ( \frac{\epsilon^2}{\pi^{2}T^{2}}\right)\right)^2} + O(\Delta^4)</math> | |||
<math>\simeq \frac{4\Delta^{2}}{\pi^{3}T^{2}}\sum_{k = 0}^{\infty}\int_{0}^{\infty}d\epsilon\frac{1}{\left ((2k+1)^2 + \epsilon^{2} \right)}</math> | |||
<math>=\frac{4\Delta^{2}}{\pi^{3}T^{2}}\sum_{k = 0}^{\infty}\frac{\pi}{4}\frac{1}{(2k +1)^{2}}</math> | |||
This series converges, and we get, | |||
<math>\ln \left (\frac{T_{c}}{T}\right) = \frac{\Delta^{2}(T)}{\pi^{2}T{2}}\frac{7\xi(3)}{8}</math> | |||
Where <math>\xi(3)</math> is the order three Reimann Zeta function. | |||
<math>\Rightarrow \frac{\Delta^{2}(T)}{\pi^{2}T{2}}\frac{7\xi(3)}{8}=-\ln \left (1+\frac{T-T_{c}}{T_{c}}\right) = \frac{T_{c}-T}{T{c}}</math> | |||
<math>\Rightarrow \Delta^{2}(T) \simeq \frac{8\pi^{2}T_{c}(T_{c}-T)}{7\xi(3)}</math> | |||
<math>\Rightarrow \Delta(T)\sim 3.063\sqrt{T_{c}(T_{c}-T)}</math> | |||
===Condensation energy and T dependence of the thermodynamic field=== | |||
<math>Z = \int D\psi^{*}D\psi\int D\Delta^{*}D\Delta e^{-S_{BCS}-S_{\Delta}}= \int D\Delta^{*}D\Delta e^{-S_{eff}[\Delta]}</math> | |||
Using the saddle point approximation | |||
<math>e^{-S_{eff}[\Delta _{0}\, ]}\; =\; e^{-S_{\Delta }}\int D\psi ^{\ast }D\psi \; e^{-S_{BCS}[\Delta _{0\, }]}\; \sim e^{-\beta F}</math> | |||
Then, | |||
<math>e^{-\beta [F(\Delta _{0})-F(0)]}</math> | |||
<math> =\frac{e^{-S_{\Delta}}\int D\psi ^{\ast }D\psi e^{-S_{BCS}[\Delta _{0}\, ]}}{\int D\psi ^{\ast }D\psi e^{-S_{BCS}[\, 0\, ]}}</math> | |||
We recall that <math>S_{\Delta }=-\frac{1}{g}\int_{0}^{\beta }d\tau \sum_{k}\Delta _{k}^{\ast }(\tau )\Delta _{k}(\tau )</math> | |||
<math>\Rightarrow S_{\Delta }(\Delta _{0})=-\frac{\Delta _{0}^{2}}{g}\beta N</math> | |||
<math> And \int D\psi ^{\ast }D\psi e^{-S_{BCS}[\Delta _{0}]}=\int D\psi ^{\ast }D\psi \, e^{-\frac{1}{\beta }}\sum_{\omega _{n}}\sum_{k}\psi _{k}^{\ast }(i\omega _{n})\begin{pmatrix} i\omega _{n}+\epsilon _{k}-\mu & \Delta _{0}\\\Delta _{0} & i\omega _{n}-\epsilon _{k}+\mu \end{pmatrix}\psi _{k}(i\omega _{n}) </math> | |||
<math>= const. \prod_{k}\prod_{n}\frac{1}{\beta ^{2}}\, \begin{vmatrix}i\omega _{n}+\epsilon _{k}-\mu & \Delta _{0}\\ \Delta _{0}& i\omega _{n}-\epsilon _{k}+\mu \end{vmatrix}</math> | |||
<math>= const. \prod_{k}\prod_{n}\frac{1}{\beta ^{2}}[(i\omega _{n})^{2}-(\epsilon _{k}-\mu )^{2}-\Delta _{0}^{2}]</math> | |||
<math>\Rightarrow e^{-\beta [F(\Delta _{0})-F(0)]}</math> | |||
<math>=\frac{e^{-\frac{\Delta _{0}^{2}}{\left | g \right |}\beta N}const.{\prod_{k}^{}} {\prod_{n}^{}}\frac{1}{\beta ^{2}}[(i\omega _{n})^{2}-(\epsilon _{k}-\mu )^{2}-\Delta _{0}^{2}]}{const.{\prod_{k}^{}}{ \prod_{n}^{}}\frac{1}{\beta ^{2}}[(i\omega _{n})^{2}-(\epsilon _{k}-\mu )^{2}]}</math> | |||
<math>=e^{-\frac{\Delta _{0}^{2}}{\left | g \right |}\beta N}{\prod_{k}^{}}{\prod_{n}^{}}(1+\frac{\Delta _{0}^{2}}{(\omega _{n}^{2})+(\epsilon _{n}-\mu )^{2}})</math> | |||
<math>=e^{-\frac{\Delta _{0}^{2}}{\left | g \right |}\beta N}e^{\sum_{k}\sum_{n}ln(1+\frac{\Delta _{0}^{2}}{\omega_{n}^{2}+(\epsilon _{n}-\mu )^{2}})}</math> | |||
<math>=e^{-\beta [F(\Delta _{0})-F(0)]}</math> | |||
Then, | |||
<math>F(\Delta _{0})-F(0)=V\frac{\Delta _{0}}{\left | g \right |}-\frac{1}{\beta } {\sum_{\omega _{n}}^{}}{\sum_{k}^{}}ln (1+\frac{\Delta _{0}^{2}}{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}})</math> | |||
Here, the first term is positive whereas the second term should be negative. | |||
In order to calculate <math>F[\Delta ]</math> we note that: | |||
<math>F[\Delta ]=-\frac{1}{\beta }{\sum_{\omega _{n}}^{}}ln(1+\frac{\Delta ^{2}}{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}})</math> | |||
<math>\frac{\mathrm{d} F[\Delta ]}{\mathrm{d} \Delta }=-\frac{1}{\beta }{\sum_{\omega _{n}}^{}}\frac{1}{(1+\frac{\Delta ^{2}}{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}})}\times \frac{2\Delta }{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}}</math> | |||
<math>-(2\Delta )\frac{1}{\beta }{\sum_{\omega _{n}}^{}}\frac{1}{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}+\Delta ^{2}}</math> | |||
Choosing <math>z=i\omega _{n}</math> | |||
<math>\frac{\mathrm{d} F[\Delta ]}{\mathrm{d}\Delta }= -(2\Delta )\frac{1}{\beta }{\sum_{\omega _{n}}^{}}\frac{1}{E_{k}^{2}-z^{2}}</math> | |||
<math>=(2\Delta ){\oint_{c}^{}}\frac{dz}{2\pi i}\frac{1}{e^{\beta z}+1}\frac{-1}{(z+E_{k})(z-E_{k})}</math> | |||
<math>=(\Delta )(\frac{n_{F(E_{k})}}{E_{k}}+\frac{n_{F}(-E_{k})}{-E_{k}})</math> | |||
<math>=(\Delta )(\frac{n_{F(E_{k})}}{E_{k}}-\frac{(1-n_{F}(E_{k}))}{E_{k}})</math> | |||
<math>=\frac{\Delta }{E_{k}}(-1+2n_{F}(E_{k}))</math> | |||
<math>\Rightarrow \int_{0}^{\Delta }d\Delta \frac{\mathrm{d}F }{\mathrm{d} \Delta }=\int d\Delta \frac{\Delta }{\sqrt{(\epsilon _{k}-\mu )^{2}+\Delta ^{2}}}(-1+2{\frac{1}{(e^{\frac{\sqrt{(\epsilon _{k}-\mu )^{2}+\Delta ^{2}}}{T}}+1)})}</math> | |||
<math>-\sqrt{(\epsilon _{k}-\mu )^{2}+\Delta ^{2}}\, +\, 4T\, ln\, [cosh\frac{(\epsilon _{k}-\mu )^{2}+\Delta ^{2}}{2T}]+const.</math> | |||
<math>\because F[0]= 0</math> | |||
<math>\therefore F[\Delta ]=-E_{k}+\left | \epsilon _{k}-\mu \right |-4T\, ln\, [\frac{1+e^{-\frac{E_{k}}{T}}}{1+e^\frac{-(\epsilon _{k}-\mu )}{T}}]</math> | |||
Using the self consistency equation: | |||
<math>\frac{1}{\left | g \right |}=\int \frac{d^{3}k}{\left ( 2\pi \right )^{3}}\frac{tanh\frac{E_{k}}{2T}}{2E_{k}}</math> | |||
<math>\therefore F[\Delta _{0}]-F[0]</math> | |||
<math>={\sum_{k}^{}}(\frac{\Delta _{0}^{2}}{2E_{k}}-E_{k}+\left | \epsilon _{k}-\mu \right |-\frac{\Delta _{0}^{2}(1-tanh\frac{E_{k}}{2T})}{2E_{k}})-4T\, ln\, (\frac{1+e^{-\frac{E_{k}}{T}}}{1+e^{-\frac{(\epsilon _{k}-\mu )}{T}}}) </math> | |||
When T= 0, only the 1st term survives. | |||
<math>\Rightarrow F[\Delta _{0}]-F[0]=-V\frac{N_{0}\Delta ^{2}}{2}</math> | |||
== Beyond saddle-point approximation, collective modes and response in the broken symmetry state== | == Beyond saddle-point approximation, collective modes and response in the broken symmetry state== | ||
| Line 1,006: | Line 2,357: | ||
<math>\begin{align} | <math>\begin{align} | ||
\Pi_{++}(q,i\Omega_n&=\frac{2}{|g|}+\frac{1}{\beta}\sum_{\omega_n}\int\frac{d^3k}{(2\pi)^3}\mbox{Tr}\left[\sigma_1G_{k+q}(i\omega_n+i\Omega_n)\sigma_1G_k(i\omega_n)\right]\\ | \Pi_{++}(q,i\Omega_n)&=\frac{2}{|g|}+\frac{1}{\beta}\sum_{\omega_n}\int\frac{d^3k}{(2\pi)^3}\mbox{Tr}\left[\sigma_1G_{k+q}(i\omega_n+i\Omega_n)\sigma_1G_k(i\omega_n)\right]\\ | ||
\Pi_{--}(q,i\Omega_n&=\frac{2}{|g|}+\frac{1}{\beta}\sum_{\omega_n}\int\frac{d^3k}{(2\pi)^3}\mbox{Tr}\left[\sigma_2G_{k+q}(i\omega_n+i\Omega_n)\sigma_2G_k(i\omega_n)\right]\\ | \Pi_{--}(q,i\Omega_n)&=\frac{2}{|g|}+\frac{1}{\beta}\sum_{\omega_n}\int\frac{d^3k}{(2\pi)^3}\mbox{Tr}\left[\sigma_2G_{k+q}(i\omega_n+i\Omega_n)\sigma_2G_k(i\omega_n)\right]\\ | ||
\Pi_{-+}(q,i\Omega_n&=-\frac{1}{\beta}\sum_{\omega_n}\int\frac{d^3k}{(2\pi)^3}\mbox{Tr}\left[\sigma_2G_{k+q}(i\omega_n+i\Omega_n)\sigma_1G_k(i\omega_n)\right]\\ | \Pi_{-+}(q,i\Omega_n)&=-\frac{1}{\beta}\sum_{\omega_n}\int\frac{d^3k}{(2\pi)^3}\mbox{Tr}\left[\sigma_2G_{k+q}(i\omega_n+i\Omega_n)\sigma_1G_k(i\omega_n)\right]\\ | ||
\end{align}</math> | \end{align}</math> | ||
| Line 1,072: | Line 2,423: | ||
<math>\Phi(x)=x^2\frac{1}{\sqrt{\pi}}\int_0^\infty d\xi\sqrt{\xi}e^{-\xi x^2}\Theta_2(0,e^{-\xi})</math> | <math>\Phi(x)=x^2\frac{1}{\sqrt{\pi}}\int_0^\infty d\xi\sqrt{\xi}e^{-\xi x^2}\Theta_2(0,e^{-\xi})</math> | ||
[[Image:Phi.jpg]] | |||
Note that | Note that | ||
| Line 1,096: | Line 2,449: | ||
What we need is | What we need is | ||
<math>\Pi_{++}(q, i\Omega_n) - \Pi_{++}(0, 0)</math> | <math>\Pi_{++}\left(q, i\Omega_n\right) - \Pi_{++}\left(0, 0\right)</math> | ||
<math>= \frac{2}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\left[\frac{1}{\omega_n^2 + E_k^2} - \frac{\omega_n\left(\omega_n + \Omega_n\right) + \left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \mu\right) - \Delta_{sp}^2}{\left(\omega_n^2 + E_k^2\right)\left(\left(\omega_n + \Omega_n\right)^2 + E_{k + q}^2\right)} - \frac{2\Delta_{sp}^2}{\left(\omega_n^2 + E_k^2\right)^2}\right]}}</math> | |||
<math>= \frac{2}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\left[\frac{\omega_n^2 + \left(\epsilon_k - \mu\right)^2 - \Delta_{sp}^2}{\left(\omega_n^2 + E_k^2\right)^2} - \frac{\omega_n\left(\omega_n + \Omega_n\right) + \left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \mu\right) - \Delta_{sp}^2}{\left(\omega_n^2 + E_k^2\right)\left(\left(\omega_n + \Omega_n\right)^2 + E_{k + q}^2\right)}\right]}}</math> | |||
<math>= \frac{2}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\left[\frac{\omega_n^2 + E_k^2 - 2\Delta_{sp}^2}{\left(\omega_n^2 + E_k^2\right)^2} - \frac{\omega_n^2 + E_k^2 + \omega_n\Omega_n + \left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \epsilon_k\right) - 2\Delta_{sp}^2}{\left(\omega_n^2 + E_k^2\right)\left(\omega_n^2 + E_k^2 + 2\omega_n\Omega_n + \Omega_n^2 + \left(\epsilon_{k + q} - \mu\right)^2 - \left(\epsilon_k - \mu\right)\right)}\right]}}</math> | |||
The second term in the brackets: | |||
<math>\frac{\omega_n^2 + E_k^2 - 2\Delta_{sp}^2 + \overbrace{\omega_n\Omega_n + \left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \epsilon_k\right)}^{\text{small}}}{\left(\omega_n^2 + E_k^2\right)\left(\omega_n^2 + E_k^2 + \underbrace{2\omega_n\Omega_n + \Omega_n^2 + \left(\epsilon_{k + q} - \mu\right)^2 - \left(\epsilon_k - \mu\right)}_{\text{small}}\right)}</math> | |||
<math>= \frac{\omega_n^2 + E_k^2 - 2\Delta_{sp}^2 + \omega_n\Omega_n + \left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \epsilon_k\right)}{\left(\omega_n^2 + E_k^2\right)^2}\left[1 + \frac{2\omega_n\Omega_n + \Omega_n^2 + \left(\epsilon_{k + q} - \epsilon_k\right)\left(\epsilon_{k + q} + \epsilon_k - 2\mu\right)}{\omega_n^2 + E_k^2}\right]^{-1}</math> | |||
Now, by Taylor expansion, | |||
<math>\epsilon_{k + q} \simeq \epsilon_k + q\cdot \nabla\epsilon_k + \ldots</math> | |||
and near the Fermi level we have | |||
<math>q\cdot \nabla\epsilon_k \simeq q\cdot v_F</math> | |||
Also note that after integrating over <math>\vec{k}</math> and <math>\omega_n</math>, terms with odd power of <math>\omega_n</math> and <math>q\cdot v_F</math> vanish. Keeping only terms of order <math>q^2</math> and <math>\Omega_n^2</math> we have | |||
<math>\frac{\omega_n^2 + E_k^2 - 2\Delta_{sp}^2}{\left(\omega_n^2 + E_k^2\right)^2}\left(1 - \frac{\Omega_n^2 + \left(q\cdot v_F\right)^2}{\omega_n^2 + E_k^2}\right) - \frac{2\omega_n^2\Omega_n^2 + 2\left(\epsilon_k - \mu\right)^2\left(q\cdot v_F\right)^2}{\left(\omega_n^2 + E_k^2\right)^3} + \frac{\omega_n^2 + E_k^2 - 2\Delta_{sp}^2}{\left(\omega_n^2 + E_k^2\right)^2}\cdot\frac{4\omega_n^2\Omega_n^2 + 4\left(\epsilon_k - \mu\right)^2\left(q\cdot v_F\right)^2}{\left(\omega_n^2 + E_k^2\right)^2}</math> | |||
The terms which we dropped are down by powers of <math>q/k_F</math> and/or vanish assuming particle-hole symmetry. | |||
<math>\begin{align} \Pi_{++}\left(q, i\Omega_n\right) - \Pi_{++}\left(0, 0\right) \simeq & \quad \frac{2}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\frac{\omega_n^2 + E_k^2 - 2\Delta_{sp}^2}{\left(\omega_n^2 + E_k^2\right)^3}\left(\Omega_n^2 + \left(q\cdot v_F\right)^2\right)}} \\ | |||
& + \frac{2}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\frac{2\omega_n^2\Omega_n^2 + 2\left(\epsilon_k - \mu\right)^2\left(q\cdot v_F\right)^2}{\left(\omega_n^2 + E_k^2\right)^3}}} \\ | |||
& - \frac{2}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3} 4 \cdot \frac{\omega_n^2 + E_k^2 - 2\Delta_{sp}^2}{\left(\omega_n^2 + E_k^2\right)^4}\left(\omega_n^2\Omega_n^2 + \left(\epsilon_k - \mu\right)^2\left(q\cdot v_F\right)^2\right)}} \\ \end{align} </math> | |||
Let's focus on <math>T = 0</math>. Then <math>\frac{1}{\beta}\sum_{\omega_n} \longrightarrow \int_{-\infty}^{\infty}{\frac{d\omega}{2\pi}}</math> <math>\Longrightarrow</math> | |||
<math>\begin{align} \Pi_{++}\left(q, i\Omega_n\right) - \Pi_{++}\left(0, 0\right) \simeq &-2N_0\int_{-\infty}^{\infty}{\frac{d\omega}{2\pi}\int_{-\infty}^{\infty}{d\xi\frac{\omega^2 + \xi^2 - \Delta_{sp}^2}{\left(\omega^2 + \xi^2 + \Delta_{sp}^2\right)^3}\left(\Omega_n^2 + q^2\langle \left(\hat{q}\cdot v_F\right)^2 \rangle_{FS}\right)}} \\ | |||
&+ 4N_0\int_{-\infty}^{\infty}{\frac{d\omega}{2\pi}\int_{-\infty}^{\infty}{d\xi\frac{\omega^2\Omega_n^2 + \xi^2q^2\langle\left(\hat{q}\cdot v_F\right)^2\rangle_{FS}}{\left(\omega^2 + \xi^2 + \Delta_{sp}^2\right)^3}}} \\ | |||
&- 8N_0\int_{-\infty}^{\infty}{\frac{d\omega}{2\pi}\int_{-\infty}^{\infty}{d\xi\frac{\omega^2 + \xi^2 - \Delta_{sp}^2}{\left(\omega^2 + \xi^2 + \Delta_{sp}^2\right)^4}\left(\omega^2\Omega_n^2 + \xi^2q^2\langle \left(\hat{q}\cdot v_F\right)^2 \rangle_{FS}\right)}} \\ \end{align}</math> | |||
So at <math>T = 0</math> : | |||
<math>\begin{align} \Pi_{++}\left(q, i\Omega_n\right) - \Pi_{++}\left(0, 0\right) \simeq & \quad 0 \\ | |||
&+ \frac{N_0}{2\Delta_{sp}^2}\left(\Omega_n^2 + q^2\langle \left(\hat{q}\cdot v_F\right)^2 \rangle_{FS}\right) \\ | |||
&- \frac{N_0}{3\Delta_{sp}^2}\left(\Omega_n^2 + q^2\langle \left(\hat{q}\cdot v_F\right)^2 \rangle_{FS}\right) \\ \end{align}</math> | |||
in 3D and for a spherical FS | |||
<math> \begin{align} \langle \left(\hat{q}\cdot v_F\right)^2 \rangle_{FS} &= \frac{v_F^2}{2}\int_{-1}^{1}{d\left(\cos\theta\right)\cos^2\theta} \\ | |||
&= \frac{v_F^2}{2}\frac{1}{3}\left(1 - \left(-1\right)\right) \\ | |||
&= \frac{v_F^2}{3} \\ \end{align}</math> | |||
<math>\Longrightarrow</math> | |||
<math>\Pi_{++}\left(q, i\Omega_n\right) - \Pi_{++}\left(0, 0\right) \simeq \frac{N_0}{6\Delta_{sp}^2}\left(\Delta_n^2 + \frac{1}{3}v_F^2q^2\right) + \ldots</math> | |||
Next | |||
<math> \begin{align} \Pi_{--}\left(q, i\Omega_n\right) &= \frac{2}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\left[\frac{1}{\omega_n^2 + E_k^2} - \frac{\omega_n\left(\omega_n + \Omega_n\right) + \left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \mu\right) + \Delta_{sp}^2}{\left(\omega_n^2 + E_k^2\right)\left(\left(\omega_n + \Omega_n\right)^2 + E_{k + q}^2\right)}\right]}} \\ | |||
&= \frac{2}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\left[\frac{1}{\omega_n^2 + E_k^2} - \frac{\omega_n^2 + \left(\epsilon_k - \mu\right)^2 + \Delta_{sp}^2 + \omega_n\Omega_n + \left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \epsilon_k\right)}{\left(\omega_n^2 + E_k^2\right)\left(\omega_n^2 + 2\omega_n\Omega_n + \Omega_n^2 + E_k^2 + \left(\epsilon_{k + q} - \mu\right)^2 - \left(\epsilon_k - \mu\right)^2\right)}\right]}} \\ | |||
&= \frac{2}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\left[\frac{1}{\omega_n^2 + E_k^2} - \frac{\omega_n^2 + E_k^2 + \omega_n\Omega_n + \left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \epsilon_k\right)}{\left(\omega_n^2 + E_k^2\right)^2\left(1 + \frac{\Omega_n^2 + 2\omega_n\Omega_n + \left(\epsilon_{k + q} - \epsilon_k\right)\left(\epsilon_{k + q} + \epsilon_k - 2\mu\right)}{\omega_n^2 + E_k^2}\right)}\right]}} \\ \end{align}</math> | |||
Now, the second term of the integrand: | |||
<math>\left[\frac{1}{\omega_n^2 + E_k^2} + \frac{\omega_n\Omega_n + \left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \epsilon_k\right)}{\left(\omega_n^2 + E_k^2\right)^2}\right]\left(1 + \frac{\Omega_n^2 + 2\omega_n\Omega_n + \left(\epsilon_{k + q} - \epsilon_k\right)\left(\epsilon_{k + q} + \epsilon_k - 2\mu\right)}{\omega_n^2 + E_k^2}\right)^{-1}</math> | |||
<math>\begin{align} = & \frac{1}{\omega_n^2 + E_k^2} - \frac{\Omega_n^2 + \left(\epsilon_{k + q} - \epsilon_k\right)^2}{\left(\omega_n^2 + E_k^2\right)^2} - \frac{2\omega_n^2\Omega_n^2 + 2\left(\epsilon_k - \mu\right)^2\left(\epsilon_{k + q} - \epsilon_k\right)^2}{\left(\omega_n^2 + E_k^2\right)^3} + \\ | |||
& \frac{1}{\omega_n^2 + E_k^2}\frac{4\omega_n^2\Omega_n^2 + 4\left(\epsilon_{k + q} - \epsilon_k\right)^2\left(\epsilon_k - \mu\right)^2}{\left(\omega_n^2 + E_k^2\right)^2} + \ldots \\ \end{align}</math> | |||
Therefore, | |||
<math>\Pi_{--}\left(q, i\Omega_n\right) \simeq \frac{2}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\left[\frac{\Omega_n^2 + \left(\epsilon_{k + q} - \epsilon_k\right)^2}{\left(\omega_n^2 + E_k^2\right)^2} - \frac{2\omega_n^2\Omega_n^2 + 2\left(\epsilon_k - \mu\right)^2\left(\epsilon_{k + q} - \epsilon_k\right)^2}{\left(\omega_n^2 + E_k^2\right)^3}\right]}}</math> | |||
Again at <math>T = 0</math> , | |||
<math>\Pi_{--}\left(q, i\Omega_n\right) \simeq 2N_0\int_{-\infty}^{\infty}{\frac{d\omega}{2\pi}\int_{-\infty}^{\infty}{d\xi\left[\frac{\Omega_n^2 + \frac{1}{3}v_F^2q^2}{\left(\omega^2 + \xi^2 + \Delta_{sp}^2\right)^2} - 2\frac{\omega^2\Omega_n^2 + \xi^2\frac{1}{3}v_F^2q^2}{\left(\omega^2 + \xi^2 + \Delta_{sp}^2\right)^3} + \ldots \right]}}</math> | |||
<math>\Pi_{--}\left(q, i\Omega_n\right) \simeq \frac{N_0}{2\Delta_{sp}^2}\left(\Omega_n^2 + \frac{1}{3}v_F^2q^2\right) + \ldots</math> | |||
Finally, | |||
<math>\begin{align} \Pi_{-+}\left(q, i\Omega_n\right) = & -\frac{1}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\frac{\left(i\omega_n + i\Omega_n\right)\left(\epsilon_k - \mu\right)\left(-2i\right) + i\omega_n\left(\epsilon_{k + q} - \mu\right)\cdot 2i}{\left[\left(\omega_n + \Omega_n\right)^2 + \left(\epsilon_{k + q} - \mu\right)^2 + \Delta_{sp}^2\right]\left[\omega_n^2 + \left(\epsilon_k - \mu\right)^2 + \Delta_{sp}^2\right]}}} \\ | |||
& = -\frac{1}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\frac{2\Omega_n\left(\epsilon_k - \mu\right) - 2\omega_n\left(\epsilon_{k + q} - \epsilon_k\right)}{\omega_n^2 + 2\omega_n\Omega_n + \Omega_n^2 + E_k^2 + \left(\epsilon_{k + q} - \epsilon_k\right)\left(\epsilon_{k + q} + \epsilon_k - 2\mu\right)} \cdot \frac{1}{\omega_n^2 + E_k^2}}} \\ | |||
& = -\frac{1}{\beta}\sum_{\omega_n}{\int{\frac{d^3k}{(2\pi)^3}\frac{2\Omega_n\left(\epsilon_k - \mu\right) - 2\omega_n\left(\epsilon_{k + q} - \epsilon_k\right)}{\left(\omega_n^2 + E_k^2\right)^2\left(1 + \frac{2\omega_n\Omega_n + \Omega_n^2 + \left(\epsilon_{k + q} - \epsilon_k\right)\left(2\left(\epsilon_k - \mu\right) + \epsilon_{k + q} - \epsilon_k\right)}{\omega_n^2 + E_k^2}\right)}}} \\ \end{align}</math> | |||
Now, expanding: | |||
<math>\left[1 + \frac{2\omega_n\Omega_n + 2\left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \epsilon_k\right) + \left(\epsilon_{k + q} - \epsilon_k\right)^2 + \Omega_n^2}{\omega_n^2 + E_k^2}\right]^{-1}</math> | |||
<math>\begin{align} = 1 & - \frac{2\omega_n\Omega_n + 2\left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \epsilon_k\right) + \left(\epsilon_{k + q} - \epsilon_k\right)^2 + \Omega_n^2}{\omega_n^2 + E_k^2} \\ | |||
& + \frac{\left[2\omega_n\Omega_n + 2\left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \epsilon_k\right) + \left(\epsilon_{k + q} - \epsilon_k\right)^2 + \Omega_n^2\right]^2}{\left(\omega_n^2 + E_k^2\right)^2} \\ | |||
& - \frac{\left[2\omega_n\Omega_n + 2\left(\epsilon_k - \mu\right)\left(\epsilon_{k + q} - \epsilon_k\right) + \left(\epsilon_{k + q} - \epsilon_k\right)^2 + \Omega_n^2\right]^3}{\left(\omega_n^2 + E_k^2\right)^3} + \ldots \\ \end{align}</math> | |||
When multiplied by <math>\Omega_n\left(\epsilon_k - \mu\right) - \omega_n\left(\epsilon_{k + q} - \epsilon_k\right)</math> and integrated over <math>\vec{k}</math> or summed over <math>\omega_n</math> all terms vanish if we assume particle-hole symmetry and <math>q/k_F \rightarrow 0</math>. That is because <math>\Omega_n\left(\epsilon_k - \mu\right) - \omega_n\left(\epsilon_{k + q} - \epsilon_k\right)</math> needs to be multiplied either by a term which is odd in <math>\epsilon_k - \mu</math> and even in <math>\epsilon_{k + q} - \epsilon_k</math> and in <math>\omega_n</math>, or by a term which is odd in <math>\omega_n</math> and <math>\epsilon_{k + q} - \epsilon_k</math> as well as even in <math>\epsilon_k - \mu</math>. But there is no such term to any order. That means that the coupling term is given by particle-hole symmetry breaking terms or terms down by <math>q/k_F</math>. | |||
With such terms present, we expect it to be <math>\sim q^2\Omega_n</math>. Although, there is a term with <math>\Omega_nN_0^'</math> | |||
<math>\left[\begin{array}{cc} \delta\Delta_+\left(-q, -i\Omega_n\right) & \delta\Delta_-\left(-q, -i\Omega_n\right) \end{array}\right]\left[\begin{array}{cc} m^2 + \frac{1}{3}\rho\left(\Omega_n^2 + c^2q^2\right) & \alpha\Omega_n \\ \alpha\Omega_n & \rho\left(\Omega_n^2 + c^2q^2\right) \end{array}\right]\left[\begin{array}{cc} \delta\Delta_+\left(q, i\Omega_n\right) \\ \delta\Delta_-\left(q, i\Omega_n\right) \end{array}\right]</math> | |||
<math>\Longrightarrow</math> | |||
<math>\begin{align} & \frac{1}{2}m^2 + \frac{2}{3}\rho\left(\Omega_n^2 + c^2q^2\right) & \pm \sqrt{\left[\frac{1}{2}m^2 - \frac{1}{3}\rho\left(\Omega_n^2 + c^2q^2\right)\right]^2 + \alpha^2\Omega_n^2} \\ | |||
\simeq & \frac{1}{2}m^2 + \frac{2}{3}\rho\left(\Omega_n^2 + c^2q^2\right) & \underbrace{\pm \left(\frac{1}{4}m^4- \frac{m^2}{3}\rho\left(\eta\Omega_n^2 + c^2q^2\right) + \ldots \right)^{\frac{1}{2}}}_{\begin{array}{clr} \Downarrow \\ \pm \frac{1}{2}m^2\left(1 - \frac{1}{3}\frac{\rho}{m^2}\left(\eta\Omega_n^2 + c^2q^2\right) + \ldots\right) \end{array}} \\ | |||
\simeq & \left\{\begin{array}{rcl} m^2 + \frac{1}{3}\left(\eta'\Omega_n^2 + c^2q^2\right) \\ \rho\left(\eta'\Omega_n^2 + c^2q^2\right) \end{array}\right. \end{align}</math> | |||
<math>\Longrightarrow</math> we have a massive propagating mode AND a massless propagating mode with velocity <math>c = \frac{v_F}{\sqrt{3}}</math>. Such a mode would have to show up in specific-heat for instance as a correction to <math>T^3</math> but it does not. Rather, we have found a (thermodynamic) sound mode of a super-fluid (which is neutral), not superconductor which is charged. | |||
==Anderson-Higgs "mechanism"== | |||
In order to properly describe the collective modes of a (charged) superconductor, we must include the effects of long-range Coulomb repulsion. That means that in addition to including the short-range attraction we must include the long-range repulsion. | |||
Latest revision as of 18:07, 3 May 2011
Welcome to Phy 6937 Superconductivity and superfluidity
PHY6937 is a one semester advanced graduate level course. Its aim is to introduce concepts and theoretical techniques for the description of superconductors and superfluids. This course is a natural continuation of the "many-body" course PHY5670 and will build on the logical framework introduced therein, i.e. broken symmetry and adiabatic continuity. The course will cover a range of topics, such as the connection between the phenomenological Ginzburg-Landau and the microscpic BCS theory, Migdal-Eliashberg treatment of phonon mediated superconductivity, unconventional superconductivity, superfluidity in He-4 and He-3, and Kosterlitz-Thouless theory of two dimensional superfluids.
The key component of the course is the collaborative student contribution to the course Wiki-textbook. Each team of students is responsible for BOTH writing the assigned chapter AND editing chapters of others.
Team assignments: Spring 2011 student teams
Outline of the course:
Pairing Hamiltonian and BCS instability
To see the origins of superconductivity, it is helpful to look at a toy system, which we already know will give us superconducting behavior. This is useful because the toy system is only a simple change to a non-interacting electron gas. By adding in some small attractive interaction, we will arrive at a superconducting system! This interaction need only occur between two electrons occupying the same position in space (and necessarily having opposite spin!). Additionally, we still find the interesting behaviour regardless of the size of the interaction; the only requirement is that it be non-zero!
Our toy model will be that of free fermions with an attractive contact interaction. We can write the Hamiltonian of the system as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_\vec{r}[\psi_\sigma^\dagger (\vec{r})(\epsilon_\vec{p}-\mu)\psi_\sigma^\dagger (\vec{r}) +g\psi_\uparrow^\dagger (\vec{r})\psi_\downarrow^\dagger (\vec{r})\psi_\downarrow (\vec{r})\psi_\uparrow (\vec{r})]}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ g<0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ |g|<<\epsilon_{F}} .
For this system, the partition function is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D[\psi_\sigma ^{*} (\tau, \vec{r}), \psi_\sigma (\tau, \vec{r})]e^{-S_{BCS}}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{BCS}=\int_0^\beta d\tau \sum_\vec{r}[\psi_\sigma^\dagger (\tau, \vec{r})(\partial _\tau+\epsilon_\vec{p}-\mu)\psi_\sigma^\dagger (\vec{r}) +g\psi_\uparrow^\dagger (\vec{r})\psi_\downarrow^\dagger (\vec{r})\psi_\downarrow (\vec{r})\psi_\uparrow (\vec{r})]}
It doesn't matter to multiply partition function by a constant:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z\rightarrow Z=\int D[\psi_\sigma ^{*} (\tau, \vec{r}), \psi_\sigma (\tau, \vec{r})] D[\Delta^{*}(\tau, \vec{r}),\Delta (\tau, \vec{r})] e^{-S_{BCS}-S_{\Delta}}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_\Delta=-\int_0^\beta d\tau\sum_{\vec{r}}\frac{1}{g}\Delta^*(\tau,\vec{r})\Delta(\tau,\vec{r})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi^\dagger} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \psi} are grassmann numbers. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Delta^*} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Delta} are normally commuting variables. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_\uparrow\psi_\downarrow} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_\downarrow\psi_\uparrow} behave like constant (paired fermions behaving like bosons).
Let's make a shift of the new integration variables:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \rightarrow \Delta+g\psi_\uparrow\psi_\downarrow}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta^*\rightarrow \Delta^*+g\psi^\dagger_\downarrow\psi^\dagger_\uparrow}
Then, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_\Delta=-\int_0^\beta d\tau \sum_{\vec{r}}\left [\frac{1}{g}\Delta^*\Delta + \Delta^*\psi_\uparrow \psi_\downarrow + \Delta\psi^\dagger_\downarrow \psi^\dagger_\uparrow+g\psi^\dagger_\downarrow \psi^\dagger_\uparrow \psi_\uparrow \psi_\downarrow\right ]}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}S=&S_{BCS}+S_{\Delta}\\ =&\int_0^\beta d\tau \sum_{\vec{r}}\{ \psi_\sigma^\dagger(\tau, \vec{r})(\partial _\tau+\epsilon_\vec{p}-\mu)\psi_\sigma^\dagger (\tau, \vec{r}) \ \ \ \ \ \ \ \ \ \ \rightarrow S_0 \\ &+\Delta^*(\tau, \vec{r})\psi_\uparrow (\tau, \vec{r})\psi_\downarrow (\tau, \vec{r}) \Delta (\tau, \vec{r})\psi^\dagger_\downarrow (\tau, \vec{r})\psi^\dagger_\uparrow (\tau, \vec{r}) \rightarrow S_{int}\\ &-\frac{1}{g}\Delta^* (\tau, \vec{r})\Delta (\tau, \vec{r}) \} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \rightarrow S_{\Delta} \end{align}}
then, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D[\psi_{\sigma}^{*}(\tau,\mathbf{r}),\psi_{\sigma}(\tau,\mathbf{r})]D[\Delta^{*}(\tau,\mathbf{r}),\Delta(\tau,\mathbf{r})]e^{-(S_{0}+S_{int.}+S_{\Delta})}} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle e^{-S_{int.}}\right\rangle _{0}\cong \exp\left [\frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}+\frac{1}{4!}\left (\left\langle S_{int.}^{4}\right\rangle _{0}-3\left\langle S_{int.}^{2}\right\rangle _{0}^{2}\right )\right ]} by cumulant expansion, which guarantees that until the 2nd order, it is accurate.
Use Matsubara's Method
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{\sigma}(\tau,\mathbf{r})=\frac{1}{\beta}\underset{\omega_{n}}{\sum}\underset{\mathbf{k}}{\sum}e^{i\mathbf{k}\cdot\mathbf{r}}e^{-i\omega_{n}\tau}\psi_{\sigma}(i\omega_{n},\mathbf{k}), \omega_{n}=(2n+1)\frac{\pi}{\beta};}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta(\tau,\mathbf{r})=\frac{1}{\beta}\underset{\Omega_{n}}{\sum}\underset{\mathbf{k}}{\sum}e^{i\mathbf{k}\cdot\mathbf{r}}e^{-i\Omega_{n}\tau}\Delta_{\mathbf{k}}(i\Omega_{n}), \omega_{n}=2n\frac{\pi}{\beta}.}
Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{0}=\frac{L^{D}}{\beta}\underset{\omega_{n}}{\sum}\underset{\mathbf{k}}{\sum}[-i\omega_{n}+\varepsilon_{\mathbf{k}}-\mu]\psi_{\sigma}^{\dagger}(i\omega_{n},\mathbf{k})\psi_{\sigma}(i\omega_{n},\mathbf{k}).}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{int.}=\frac{L^{D}}{\beta^{2}}\underset{\omega_{n},\Omega_{n}}{\sum}\underset{\mathbf{k},\mathbf{q}}{\sum}[\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\psi_{\uparrow}(i\Omega_{n}-i\omega_{n},\mathbf{\mathbf{q}-k})\psi_{\downarrow}(i\omega_{n},\mathbf{k})+\Delta_{\mathbf{q}}(i\Omega_{n})\psi_{\downarrow}^{\dagger}(i\omega_{n},\mathbf{k})\psi_{\uparrow}^{\dagger}(i\Omega_{n}-i\omega_{n},\mathbf{\mathbf{q}-k})].}
The Fourier transform of 1 body Green's function is (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=1,2} mean Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbf{r}_{i},\tau_{i}}} ) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(1-2)=\left\langle \psi(1)\psi^{*}(2)\right\rangle =\frac{1}{\beta}\underset{\omega_{n}}{\sum}\frac{1}{L^{D}}\underset{\mathbf{k}}{\sum}e^{-i\omega_{n}(\tau_{1}-\tau_{2})}e^{i\mathbf{k}\cdot(\mathbf{r}_{1}-\mathbf{r}_{2})}\frac{1}{-i\omega_{n}+\varepsilon_{\mathbf{k}}-\mu}} ,
so Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\sigma}^{0}(i\omega_{n},\mathbf{k})=\left\langle \psi_{\sigma}(i\omega_{n},\mathbf{k})\psi_{\sigma}^{\dagger}(i\omega_{n},\mathbf{k})\right\rangle _{0}=\frac{\beta}{L^{D}}\frac{1}{-i\omega_{n}+\varepsilon_{\mathbf{k}}-\mu}} .
Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle S_{int.}^{2}\right\rangle _{0}=\frac{2L^{2D}}{\beta^{4}}\underset{\omega_{n},\Omega_{n}}{\sum}\underset{\mathbf{k},\mathbf{q}}{\sum}[G_{\uparrow}^{0}(i\omega_{n},\mathbf{k})G_{\downarrow}^{0}(i\Omega_{n}-i\omega_{n},\mathbf{q}-\mathbf{k})]\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})=L^{D}\frac{2}{\beta}\underset{\Omega_{n},\mathbf{q}}{\sum}\chi_{p}(\mathbf{q},i\Omega_{n})\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})} ,
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{p}(\mathbf{q},i\Omega_{n})=\frac{L^{D}}{\beta^{3}}\underset{\omega_{n},\mathbf{k}}{\sum}G_{\uparrow}^{0}(i\omega_{n},\mathbf{k})G_{\downarrow}^{0}(i\Omega_{n}-i\omega_{n},\mathbf{q}-\mathbf{k})} is called pairing susceptibility.
Let's calculate it:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{p}(\mathbf{q},i\Omega_{n})=\frac{L^{D}}{\beta^{3}}\underset{\omega_{n},\mathbf{k}}{\sum}G_{\uparrow}^{0}(i\omega_{n},\mathbf{k})G_{\downarrow}^{0}(i\Omega_{n}-i\omega_{n},\mathbf{q}-\mathbf{k})=\frac{1}{L^{D}}\frac{1}{\beta}\underset{\omega_{n},\mathbf{k}}{\sum}\frac{-1}{i\omega_{n}-\varepsilon_{\mathbf{k}}+\mu}\times\frac{1}{i\omega_{n}-i\Omega_{n}+\varepsilon_{\mathbf{q}-\mathbf{k}}-\mu}} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow=\frac{1}{L^{D}}\frac{1}{\beta}\underset{\mathbf{k}}{\sum}\oint_{c}\frac{dz}{2\pi i}\frac{-1}{z-\varepsilon_{\mathbf{k}}+\mu}\times\frac{1}{z-i\Omega_{n}+\varepsilon_{\mathbf{q}-\mathbf{k}}-\mu}\frac{1}{e^{\beta z}+1}} .
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-1}{z-\varepsilon_{\mathbf{k}}+\mu}\times\frac{1}{z-i\Omega_{n}+\varepsilon_{\mathbf{q}-\mathbf{k}}-\mu}=\frac{1}{\varepsilon_{\mathbf{q}-\mathbf{k}}+\varepsilon_{\mathbf{k}}-2\mu-i\Omega_{n}}[\frac{1}{z-\varepsilon_{\mathbf{q}}+\mu}-\frac{1}{z-i\Omega_{n}+\varepsilon_{\mathbf{q}-\mathbf{k}}-\mu}]} ,
and change the integral path to
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow=-\frac{1}{L^{D}}\frac{1}{\beta}\underset{\mathbf{k}}{\sum}\frac{1}{\varepsilon_{\mathbf{q}-\mathbf{k}}+\varepsilon_{\mathbf{k}}-2\mu-i\Omega_{n}}[\frac{1}{e^{\beta(\varepsilon_{\mathbf{q}}-\mu)}+1}-\frac{1}{e^{\beta(-\varepsilon_{\mathbf{q}-\mathbf{k}}+\mu)}+1}]=\int\frac{d^{D}k}{(2\pi)^{D}}\frac{1}{\varepsilon_{\mathbf{q}}+\varepsilon_{\mathbf{q}-\mathbf{k}}-2\mu-i\Omega_{n}}[1-f(\varepsilon_{\mathbf{k}})-f(\varepsilon_{\mathbf{q}-\mathbf{k}})].}
In the static (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Omega_{n}=0} ) and uniform (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{q}=0} ) limit,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-2f(\varepsilon_{\mathbf{k}})=\tanh[\frac{\beta}{2}(\varepsilon_{\mathbf{k}}-\mu)]} .
Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{p}(0,0)=\int\frac{d^{D}k}{(2\pi)^{D}}\frac{\tanh[\frac{\beta}{2}(\varepsilon_{\mathbf{k}}-\mu)]}{2(\varepsilon_{\mathbf{k}}-\mu)}} .
In low energy, integrate the energy in the shell near Fermi energy:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow\chi_{p}(0,0)\cong N(0)\int_{\hbar\omega_{D}}^{-\hbar\omega_{D}}d\xi\frac{\tanh[\xi\beta/2]}{2\xi}\cong N(0)\int_{0}^{-\hbar\omega_{D}}d\xi\frac{\tanh[\xi\beta/2]}{\xi}=N(0)\ln[\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T}].}
Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}=L^{D}\frac{1}{\beta}\chi_{p}(0,0)\underset{\Omega_{n},\mathbf{q}}{\sum}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})} .
If we ignore the higher order in the cumulant expansion,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{eff}=-\underset{\mathbf{r}}{\sum}\int_{0}^{\beta}d\tau\frac{1}{g}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})-\frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}=\underset{\mathbf{r}}{\sum}\int_{0}^{\beta}d\tau[\frac{1}{\left|g\right|}-N(0)\ln(\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T})]\Delta^{*}(\tau,\mathbf{r})\Delta(\tau,\mathbf{r})} .
Remember the partition function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D\Delta^{*}D\Delta e^{-S_{eff}(\Delta)}} . To look at superconductivity, we really only must consider the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} related factors.
The superconductivity phase transition temperature is the temperature that makes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\frac{1}{\left|g\right|}}-N(0){\ln(\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T})}=0}
,
which happens at
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{c}=\frac{\hbar\omega_{D}}{k_{B}}\frac{2}{\pi}e^{\gamma}e^{-\frac{1}{N(0)\left|g\right|}}=1.134\frac{\hbar\omega_{D}}{k_{B}}e^{-\frac{1}{N(0)\left|g\right|}}}
.
Above this critical temperature, the coefficient of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta^*\Delta} term becomes positive, and it is energetically unfavorable to have cooper pairs, as in the normal state. Below the critical temperature, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} related factors in the partition function will diverge, which means superconductivity phase transition. Notice that this happens for any value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |g|} ! No matter how small the attraction between our fermions is, we can still find this funny (as of yet, it has not been shown to be specifically superconducting!) behaviour.
Finite Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{q}} (small) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ (\Omega_n=0)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_p (q,0)-\chi_p (0,0)=\frac{1}{L^D} \sum_k \frac{1}{\beta} \sum_{i\omega_n}\frac{-1}{i\omega_n-\epsilon_k+\mu}(\frac{1}{i\omega_n+\epsilon_{q-k}-\mu}-\frac{1}{i\omega_n+\epsilon_{-k}-\mu}) }
for small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{q}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{q-k}=\epsilon_{-k}+q\frac{\partial \epsilon_\rho}{\partial \rho}|_{\rho=-k}=\epsilon_\vec{k}+\vec{q}\cdot \vec{v}_{-k}=\epsilon_k-\vec{q}\cdot\vec{v}_k}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{i\omega_n+\epsilon_k-\mu-q\cdot v_k}=\frac{1}{i\omega_n+\epsilon_k-\mu}+\frac{q\cdot v_k}{(i\omega_n+\epsilon_k-\mu)^2}+\frac{(q\cdot v_k)^2}{(i\omega_n+\epsilon_k-\mu)^3}}
Thus,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}\chi_p(q,0)-\chi_p(0,0) &=\frac{1}{L^D}\sum_k\frac{1}{\beta}\sum_{i\omega_n}\frac{-1}{i\omega_n-\epsilon_k+\mu}\left(\frac{q\cdot v_k}{(i\omega_n+\epsilon_k-\mu)^2}+\frac{(q\cdot v_k)^2}{(i\omega_n+\epsilon_k-\mu)^3}+...\right) \\ &=\frac{-1}{\beta}\sum_i\omega_n \int \frac{d^D k}{(2\pi)^D}\frac{(\vec{q}\cdot \vec{v}_k)^2}{(i\omega_n-\epsilon_k+\mu)(i\omega_n+\epsilon_k-\mu)^3} \end{align}}
Consider the states near the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar \omega_D} shell near fermi surface, we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_p(q,0)-\chi_p(0,0) =\frac{1}{\beta}\sum_{i\omega_n}\int\frac{d\Omega_{F.S.}}{\Omega_D}(q\cdot v_F)^2\int_{-\infty}^{+\infty} d\xi N(\xi+\mu)\frac{1}{(\xi-i\omega_n)(\xi+i\omega_n)^3}}
where, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \xi=\epsilon_k-\mu}
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int_{-\infty}^{+\infty} d\xi \frac{1}{(\xi-i\omega_n)(\xi+i\omega_n)^3} &=\frac{2\pi i}{(2i\omega_n)^3}\theta(\omega_n)-\frac{2\pi i}{(2i\omega_n)^3}\theta(-\omega_n)\\ &=\frac{2\pi i}{(2i|\omega|)^3} \end{align} }
So,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \chi_p(q,0)-\chi_p(0,0) &=\frac{1}{\beta}\sum_{i\omega_n}N(0)\int\frac{d\Omega}{\Omega_D}(q\cdot v_F)^2\frac{2\pi i}{(2i|\omega|)^3}\\ &=N(0)v_F^2|\vec{q}|^2\int\frac{d\Omega}{\Omega_D}(q\cdot v_F)^2 \frac{1}{\beta}\sum_{i\omega}\frac{2\pi i}{-8i|\frac{(2n+1)\pi}{\beta}|^3}\\ &=-\frac{1}{4}N(0)v_F^2q^2(<(\hat{q}\cdot \hat{v_F})>_{F.S.})\frac{\beta^2}{\pi^2}(\sum_{N=-\infty}^{+\infty}\frac{1}{|2n+1|^3}) \end{align} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{N=-\infty}^{+\infty}\frac{1}{|2n+1|^3}=\sum_{n=0}^\infty\frac{2}{(2n+1)^3}=\frac{2}{\pi}\frac{7\zeta(3)}{8} }
where, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \zeta(3)} is Riemann zeta function.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <(\hat{q}\cdot \hat{v}_F)^2>_{F.S.}=\frac{1}{D} }
For spherical F.S. in 3D,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\frac{d\Omega}{\Omega_D}(\hat{q}\cdot\hat{v}_F)^2=\frac{2\pi}{4\pi}\int_{-1}^{1}d(\cos{\theta})\,\cos^2{\theta} = \frac{1}{3} }
For circular F.S. in 2D,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\frac{d\Omega}{\Omega_D}(\hat{q}\cdot\hat{v}_F)^2=\frac{1}{2\pi}\int_{0}^{2\pi}d\theta\,\cos^2{\theta} = \frac{1}{2} }
Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \chi_p(q,0)-\chi_p(0,0) &=-\frac{1}{4}N(0)v_{F}^{2}q^{2}\frac{1}{D}\frac{\beta^{2}}{\pi^{2}}\frac{2}{\pi}\frac{7\zeta(3)}{8} \\ &=-N(0)\frac{7\zeta(3)}{16D\pi^{2}}q^{2}\frac{1}{\pi \hbar^{2}}\left(\frac{\hbar v_{F}}{k_{B}T}\right)^{2} \\ &\equiv-N(0)q^{2}\xi^{2} \end{align} }
So
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{1}{2}\left\langle S_{int.}^{2}\right\rangle _{0}&=L^{D}\frac{1}{\beta}\underset{\Omega_{n},\mathbf{q}}{\sum}\chi_{p}(q,0)\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n}) \\ &=N(0)\ln[\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T}]L^{D}\frac{1}{\beta}\underset{\Omega_{n},\mathbf{q}}{\sum}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n})-L^{D}\frac{1}{\beta}\underset{\Omega_{n},\mathbf{q}}{\sum}N(0)q^{2}\xi^{2}\Delta_{\mathbf{q}}^{*}(i\Omega_{n})\Delta_{\mathbf{q}}(i\Omega_{n}) \end{align} } .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{eff}=\underset{\mathbf{r}}{\sum}\int_{0}^{\beta}d\tau\left[\left(\frac{1}{\left|g\right|}-N(0)\ln(\frac{2\hbar\omega_{D}e^{\gamma}}{\pi k_{B}T})\right)\Delta^{*}(\tau,\mathbf{r})\Delta(\tau,\mathbf{r})-N(0)\xi^{2}(\nabla\cdot\Delta^{*}(\tau,\mathbf{r}))(\nabla\cdot\Delta(\tau,\mathbf{r}))\right]} .
Note that the last term in the expression tells us that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{eff} } would increase if gradient of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta } is not zero.
Note that the above expression has a one-one correspondant to the Giznburg-Landau functional:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=\int d^{D}r\left[ \alpha (T-T_{c}) |\Psi(\vec{r})|^{2}+\frac{\hbar^{2}}{2m^{*}}|\nabla \Psi(\vec{r})|^{2} \right] } ,
here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Psi(\vec{r}) } corresponds to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \frac{\Delta(\tau,\vec{r})}{|g|N(0)a_{0}} } in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{eff}} .
Little Parks experiment
As shown in the above figure, a thin shell of superconductor with radius R is placed in a small uniform magnetic field passing through the hollow center of the cylinder. The experiment intends to show the variation of the critical temperature with change of the magnetic field passing through the hollow superconductor cylinder. This was done in 1962, by Little and Parks at Stanford University.
Before showing the mathematics behind the experiment, we first have to rewrite the Giznburg-Landau functional to take the presence of magnetic field into account. The Hamiltonian for a free electron moving in a magnetic field is written as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2m}(p+\frac{eA}{c})^{2}\psi + V\psi = E\psi }
The physically observable magnetic field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{B}} would remain the same if we choose a different vector potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\rightarrow A+ \nabla \chi } (or perform a gauge transformation). To maintain the same eigen-energy E which is observable, the wave function has to undergo a phase change: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi \rightarrow e^{i\phi}\psi } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi=\frac{e}{c\hbar}\chi }
Now in our effective action, the wave function appears as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta^{*}(\tau,\vec{r})\psi_\uparrow (\tau,\vec{r})\psi_\downarrow (\tau,\vec{r}) + \Delta(\tau,\vec{r}) \psi_\downarrow^\dagger (\tau,\vec{r})\psi_\uparrow^\dagger (\tau,\vec{r}) }
since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi \rightarrow e^{i\phi}\psi } , if we want the effective action to remind the same, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Delta } has to transform as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \rightarrow e^{-2i\phi}\Delta }
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Delta } corresponds to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Psi } in the Giznburg-Landau functional, so the Giznburg-Landau functional is modified as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=\int d^{D}r\left[ \alpha (T-T_{c}) |\Psi(\vec{r})|^{2}+\frac{1}{2m^{*}}| ( \frac{\hbar \nabla}{i} - \frac{2e}{c}A(\vec{r}) ) \Psi(\vec{r})|^{2} \right] }
Note that the last term looks like a particle of charge Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2e} in a magnetic field!
Now, we choose the symmetric gauge:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{A}=\frac{1}{2}\vec{H}\times\vec{r}=\frac{1}{2}Hr\hat{\phi} }
Re-write in cylindrical coordinates:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\nabla}=\hat{r}\frac{\partial}{\partial r} + \frac{\hat{\phi}}{r}\frac{\partial}{\partial \phi} + \hat{z}\frac{\partial}{\partial z} }
Define the unit flux as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{0}=\frac{hc}{2e} }
Define the fluxoid as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(R) = \pi HR^{2}\ } , so we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} F&=\int d^{D}r\left[ \alpha (T-T_{c})|\Psi(\vec{r})|^{2} +\frac{\hbar^{2}}{2m^{*}}| (\frac{1}{R}\frac{\partial}{\partial \phi} - \frac{ie}{\hbar c} HR )\Psi(\vec{r}) |^{2}+ \frac{\hbar^{2}}{2m^{*}}|\frac{\partial}{\partial z} \Psi(\vec{r}) |^{2} \right] \\ &=\int d^{D}r\left[ \alpha (T-T_{c})|\Psi(\vec{r})|^{2} +\frac{\hbar^{2}}{2m^{*}R^{2}}| (\frac{\partial}{\partial \phi} - \frac{i\Phi}{\Phi_{0}} )\Psi(\vec{r}) |^{2} \right] \\ \end{align} }
When Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi = N\Phi_{0}\ } , the critical temperature will remain the same and the phase of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi\ } is changed as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi \rightarrow e^{iN\phi} \Psi } . When Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi \neq N\Phi_{0}\ } , the critical temperature is found to vary as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{c}^{new}=T_{c}- \frac{\hbar^{2}}{2m^{*}R^{2}\alpha}\left (N-\frac{\Phi}{\Phi_{0}}\right )^{2}} . See the figure below.
This experiment is significant evidence that the objects represented by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} carry a charge twice that of a single electron. As we know that this thing stands in the equations for a cooper pair, this makes perfect sense!
Microscopic derivation of the Ginzburg-Landau functional
Let us consider the model of a metal close to the transition to the superconducting state. A complete description of its thermodynamic properties can be done through the calculation of the partition function.
Ginzburg-Landau Functional
The classical part of the Hamiltonian in the partition function, dependent of bosonic fields, may be chosen in the spirit of the Landauer theory of phase transition. However, in view of the space dependence of wave functions, Ginzberg and Landauer included in it additionally the first non vanishing term of the expansion over the gradient of the fluctuation field. Symmetry analysis shows that it should be quadratic. The weakness of the field coordinate dependence permits to omit the high-order terms of such an expansion. Therefore, the classical part of the Hamiltonian of a metal close to a superconducting transition related to the presence of the fluctuation Cooper pairs in it (the so called Ginzberg-Landauer functional)can be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F[\psi(r)]=F_{n}+\int dV\{a\mid\psi(r)\mid^{2}+\frac{b}{2}\mid\psi(r)\mid^{4}+\frac{1}{4m}\mid\nabla\psi(r)\mid^{2}\}}
The basic postulate of G-L is that if is small and varies slowly in space, so we can expand the free energy in a series of .These two terms should be adequate so long as one stays near the second-order phase transition at , where the order parameter . Inspection of G-L functional shows that must be positive if the theory is to be useful; otherwise the lowest free energy would occur for arbitrarily large values of , where the expansion is surely inadequate.
We already got the quadratic terms in the Ginzberg-Landauer by expanding to the second order, and we are going to go the higher order. As we discussed, we expect that this term will be a negative value to keep as a negative value under . To catch this goal we start with the partition function:
where
we can expand this average for small near , for this perpose we can assume a second order phase transition so that it increases continiously from zero to finite number after .
we need to calculate the average of which can be calculated by Tylor expansion:
=
In this expansion all odd power terms go to zero because when we calculate the integral over and its complex conjugate it will vanish since we have odd numbers of or in the integral. Then, we try to approximate it to .
if we expand these two terms in to the second order the following expression can be got:
can be chose in a such way that this result will match to the original expansion of up to the forth power of :
so,
according to the expression we got before:
let's write in terms of for simplification. where
is a couple Grassman number, so we do not need to be worry about the sign when these terms commute with other terms.
By Feynman diagram, has:
Recall the Fourier transform of one body Green function is:
To seek solution of which are independent using Feynman diagram
after getting integration over we will get and similarly by getting integration over we have
So, the final result can be written:
Now, we wish to perform gradiant expansion:
where:
integrate over gives us:
and similarly :
because of timereversal symetry.
We can substitute the sum using
So, we get a term that is always negative and it corresponds to the in the Ginzberg-Landauer functional.
Saddle Point Approximation
Starting from the microscopic model, we found that , where the order in , and keeping only quadratic qradient terms, we have:
We can use this expression to make quantitative experimental predictions. The path integral over is still imposible to carry out exactly, despite our approximations for , because contains quartic terms in and so we are not dealing with a Gaussian integral. The approximation strategy whic we will pursue is called saddle point approxiation, which in our contetxt means that we will expand teh integrand about a solution which minimizes S_{eff} with respect to . What we end up doing is replacing Z with , where is determined from At this point, let's seek uniform solutions to their equations, in whcih case we can drop the gradient terms in : where: and
Note that for : and
So Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\Delta_{min}+B\Delta_{min}^{3}=0} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_{min}=0, \;T>T_{C}} and
.
,
Since, we now have the approximate expression for the partition function we can calculate thermodynamic physical properties. the one we will focus on is the specific heat. Recall that,
if we only study the constribution to from the superconducting order parameter terms in , we have So, we see that if the double derivateive of with respect to is finite at , then the specific heat jumps at , since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{V}=0} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T>T_{C}} . We are interested in the size of this jump. Therefore, we need to simply expand Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-A^{2}}{2B}} near Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{C}} . Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} vanishes at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{C}} , we can simply evaluate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{C}} and expand Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(T)=\frac{1}{|g|}-N(0)ln\left(\frac{\hbar\omega_{D}}{k_{B}\left(T_{C}+T-T_{C}\right)}\frac{2e^{\gamma}}{\pi}\right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{1}{|g|}-N(0)ln\left(\frac{2e^{\gamma}}{\pi}\frac{\hbar\omega_{D}}{k_{B}T_{C}}\left(1+\frac{T-T_{C}}{T_{C}}\right)^{-1}\right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\underset{vanishes\; by\; def.\; of\; T_{C}}{\underbrace{\frac{1}{|g|}-N(0)ln\left(\frac{2e^{\gamma}}{\pi}\frac{\hbar\omega_{D}}{k_{B}T_{C}}\right)}}by+N(0)ln\left(1+\frac{T-T_{C}}{T_{C}}\right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow A(T)=N(0)ln\left(1+\frac{T-T_{C}}{T_{C}}\right)\simeq N(0)\frac{T-T_{C}}{T_{C}}+...}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow\frac{-A^{2}(T)}{2B(T)}\simeq-\frac{1}{2}\frac{N^{2}(0)\left(\frac{T-T_{C}}{T_{C}}\right)^{2}}{\frac{7\zeta(3)}{8\pi}\frac{N(0)}{k_{B}^{2}T^{2}}}+...}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta c_{V}\simeq-\frac{T_{C}}{2}\frac{8\pi^{2}}{7\zeta(3)}k_{B}^{2}N(0)+...}
What is the specific heat of a non-interacting electron gas?
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{V}^{(n)}=\frac{\partial}{\partial T}\left(2(from\; spin)\int\frac{d^{D}k}{(2\pi)^{D}}\frac{\left(\epsilon_{k}-\mu\right)}{e^{\frac{\epsilon_{k}-\mu}{k_{B}T}+1}}\right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =2\int\frac{d^{D}k}{(2\pi)^{D}}\frac{-\left(\epsilon_{k}-\mu\right)}{\left(e^{\frac{\epsilon_{k}-\mu}{k_{B}T}+1}\right)^{2}}\left(\frac{-\left(\epsilon_{k}-\mu\right)}{k_{B}T^{2}}\right)e^{\left(\frac{\epsilon_{k}-\mu}{k_{B}T}\right)}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \simeq2k_{B}N(0)\int_{-\infty}^{\infty}d\xi\left(\frac{\xi}{2k_{B}T}\right)^{2}\frac{1}{cosh^{2}\left(\frac{\xi}{2k_{B}T}\right)}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \simeq4k_{B}^{2}TN(0)\underset{\frac{\pi^{2}}{6}}{\underbrace{\int_{-\infty}^{\infty}dx\frac{x^{2}}{cosh^{2}x}}}=\frac{2\pi^{2}}{3}k_{B}^{2}T}
So, if we measure the jump in the specific heat at T_c in the units of the normal state electronic contribution we find: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\Delta c_{V}}{c_{V}^{(n)}}=\frac{\frac{8\pi^{2}}{7\zeta(3)}k_{B}^{2}T_{C}N(0)}{\frac{2\pi^{2}}{3}k_{B}^{2}T_{C}N(0)}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{12}{7\zeta(3)}\simeq1.426} This is dimensionless number is a “famous” prediction of the BCS theory, although we derived it using different formalism. Let's check it with experiment:
First the caveats:
when specific is measured, all excitations contribute. Most importantly lattice vibrations (phonons) contribute as well. At low T, however, the phonon contribution drops of as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T^3} and we can neglect it if the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_C} is sufficiently low. In practice we have do an example:
| materials | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_C} | phonon contribution at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_C} |
| Al | 1.2K | 1% |
| Zn | 0.8K | 3% |
| Cd | 0.5K | 3% |
| Sn | 3.7K | 45% |
| In | 3.4K | 77% |
| Th | 2.4K | 83% |
| Pb | 7.2K | 94% |
Experimental data for Aluminum gives
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\Delta c_{V}}{c_{V}^{(n)}}\simeq 1.39}
This result from the saddle point approximation/mean field is very close to the experimental result. But for high Tc superconductor the behavior is very different. The heat capacity of superconductor decrease gradually, doesn't have sharp jump like in the picture below. The Gaussian approximation we have used is not enough to explain high Tc superconductor.
Limitation of Microscopic derivation of the Ginzburg-Landau functional
1) Fluctuation is important in low dimension (such in 2D by including Gaussian fluctuation)
2) In 1D, beyond mean field approach is needed
3) Mean Field give jump in second order of the derivative
4) We need to include fluctuation in High Tc superconductor
5) Gaussian approximation is not enough in High Tc superconductor
Effects of an applied magnetic field; Type I and Type II superconductivity
Derivation of the Ginzburg-Landau equations
Our starting point will be the Ginzburg-Landau (GL) free energy in the presence of an external magnetic field,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=\int d^d \vec{r} \left [\alpha(T-T_c)|\Psi(\vec{r})|^2+\tfrac{1}{2}b|\Psi(\vec{r})|^4+\frac{\hbar^2}{2m}\left |\left (\nabla-i\frac{2e}{\hbar c}\vec{A}(\vec{r})\right )\Psi(\vec{r})\right |^2+\frac{1}{8\pi}(\nabla\times\vec{A}(\vec{r}))^2-\frac{1}{c}\vec{J}_{\text{ext}}(\vec{r})\cdot\vec{A}(\vec{r})\right ],}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{A}} is the total vector potential and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_{\text{ext}}} is an external current density, assumed to be controlled experimentally. This current satisfies
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla\times\vec{H}=\frac{4\pi}{c}\vec{J}_{\text{ext}},}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{H}} is the external magnetic field. The expression is the sum of the energy due to the superconducting order parameter, with the magnetic field introduced via the gauge invariance argument given above, the energy of the magnetic field alone, and the work done by the superconductor to maintain the external current at a constant value.
Let us first derive the "saddle point" equations satisfied by the magnetic field in the normal state. In this case, we set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi} to zero everywhere and set
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left. \frac{\delta F}{\delta\vec{A}(\vec{r})}\right |_{\vec{A}=\vec{A}_\text{min}}=0.}
We will find this derivative by first finding the variation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta F} in the free energy for this case, which is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta F=\int d^d \vec{r}' \left [\frac{1}{4\pi}(\nabla\times\vec{A}(\vec{r}'))\cdot(\nabla\times\delta\vec{A}(\vec{r}'))-\frac{1}{c}\vec{J}_{\text{ext}}(\vec{r}')\cdot\delta\vec{A}(\vec{r}')\right ],}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta\vec{A}} is a small variation in the vector potential; we assume that it vanishes on the "surface" of our system. We now transform the first term using the identity,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\nabla\times\vec{A})\cdot(\nabla\times\vec{B})=\nabla\cdot[\vec{A}\times(\nabla\times\vec{B})]+\vec{A}\cdot[\nabla\times(\nabla\times\vec{B})],}
obtaining
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta F=\int d^d \vec{r}' \left [\frac{1}{4\pi}\nabla\cdot[\delta\vec{A}(\vec{r}')\times(\nabla\times\vec{A}(\vec{r}'))]+\frac{1}{4\pi}\delta\vec{A}(\vec{r}')\cdot[\nabla\times(\nabla\times\vec{A}(\vec{r}'))]-\frac{1}{c}\vec{J}_{\text{ext}}(\vec{r}')\cdot\delta\vec{A}(\vec{r}')\right ].}
The first term is a "surface" term; since we assumed that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta\vec{A}} vanishes everywhere on the "surface", we are left with just
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta F=\int d^d \vec{r} \left [\frac{1}{4\pi}[\nabla\times(\nabla\times\vec{A}(\vec{r}'))]-\frac{1}{c}\vec{J}_{\text{ext}}(\vec{r}')\right ]\cdot\delta\vec{A}(\vec{r}').}
We conclude that the variational derivative that we are interested in is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta F}{\delta\vec{A}(\vec{r})}=\frac{1}{4\pi}[\nabla\times(\nabla\times\vec{A}(\vec{r}'))]-\frac{1}{c}\vec{J}_{\text{ext}}(\vec{r}').}
At the "saddle point", this derivative is zero, so we obtain the equation,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla\times(\nabla\times\vec{A})=\frac{4\pi}{c}\vec{J}_{\text{ext}}.}
We may introduce the total magnetic field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{B}=\nabla\times\vec{A}} , thus obtaining
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla\times\vec{B}=\frac{4\pi}{c}\vec{J}_{\text{ext}}.}
Comparing this to the definition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J}_{\text{ext}}} given above, we conclude that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{B}=\vec{H}} in the normal state. In reality, this will only be approximately true due to para- or diamagnetic effects in the metal, but these effects will be small in comparison to those due to superconductivity, which we will now derive.
First, we will apply the "saddle point" condition for the superconducting order parameter, , which is
Again, we start by finding the variation in the free energy in terms of a small variation in the order parameter:
The last term is equal to
The second term in this expression is a "surface" term. If we assume that is zero on the "surface", then this term vanishes, leaving us with
We can now immediately write down the variational derivative, which, upon being set to zero, gives us the first GL equation,
We also need to minimize the free energy with respect to the magnetic field. We have already done this for the normal case, and there is only one more term that we need to consider in the superconducting case; we will therefore only treat this term. We can quickly write down the variation in the superconducting part of the free energy , which is
Combining this result with the previous result for the normal metal, we obtain the second GL equation,
or, introducing and ,
Given the definition of and the Maxwell equation (assuming static fields),
where is the total current density, we conclude that the left-hand side of this equation is the current density induced inside the superconductor.
Let us now suppose that we do not assume that vanishes on the surface. It may then be shown that the following boundary condition holds on the surface (see P. G. de Gennes, Superconductivity in Metals and Alloys):
This relation holds for a superconductor-metal interface; for a superconductor-insulator interface, . We may show that this condition implies that the normal component of the current density on the surface vanishes. If we multiply the above condition by on both sides, we obtain
Taking the complex conjugate of both sides gives us
Adding these two equations together gives us
The left-hand side is proportional to the normal component of the current density inside the superconductor.
The GL Equations in Dimensionless Form
We will find it convenient to introduce dimensionless variables when working with the GL equations. We start by introducing a dimensionless order parameter, , where
We may rewrite the first GL equation in terms of this parameter as
and the second as
where we re-introduced into the right-hand side and also introduced , defined as
Next, we introduce a dimensionless position vector,
where is known as the penetration depth of the superconductor; we will see where this name comes from shortly. In terms of this vector, the first GL equation becomes
and the second becomes
Finally, we introduce a dimensionless vector potential,
and the dimensionless parameter,
In terms of these, the first GL equation becomes
and the second becomes
We see that our theory has a dimensionless parameter in it, namely , which is known as the Ginzburg-Landau parameter. We may write this parameter as
where
is the GL coherence length. This tells us that is the ratio of two length scales associated with the superconductor, namely the scale over which the order parameter "heals" (the coherence length ) and that over which the magnetic field dies out (the penetration depth , as we will demonstrate shortly). It also turns out that this parameter decides what type of superconductor we are dealing with. If , then we have a Type I superconductor, while, if , then we have a Type II superconductor.
We may now find the value of this parameter in the microscopic model we considered earlier. In that case, we found that
where is the density of states at the Fermi level, is the coherence length, is the number of dimensions that we are working in, and is the thermal wavelength. We will state the result for . Given that
and that, in this case,
we find that
Note that we set in the expression for ; this is because the GL theory is only valid just below the transition temperature. We may also express this in terms of the Fermi energy,
Doing so, we obtain
In a typical metal, so
A Simple Example - The Strongly Type-I Superconductor With a Planar Surface
As a simple demonstration of the solution of the GL equations, let us consider a strongly Type I () superconductor with a planar boundary between it and an insulator. Let us set up our coordinate system so that the boundary is at .
We apply a magnetic field along the axis,
We expect by symmetry that the total magnetic field . We will choose our gauge such that
We also take the order parameter to depend only on . The first GL equation becomes
Since we are taking to be small, the derivative term dominates, and we may therefore approximate this equation as
so that . Our boundary condition states that
so that . Since in the bulk, we conclude that for . Similarly, deep into the insulating region, so that for .
Now we consider the second equation. In this case, it becomes, for ,
or
The right-hand side is just
so that the equation is now
The solution to the equation in simply , or, in terms of dimensional quantities,
Since our superconductor is in the region , we must take . Furthermore, the field must equal the applied field at , so
For , the second GL equation becomes
The solution, in terms of dimensional quantities, is . We must set so that the field does not increase indefinitely as we move away from the superconductor. Since in the normal state, we conclude that for . The following is a plot of the full dependence of the magnetic field on position.
We have now shown why we called the penetration depth; it sets the length scale over which the magnetic field tends to zero inside the superconductor. We have also illustrated the expulsion of applied magnetic fields from the bulk of a Type I superconductor; this is known as the Meissner effect.
Thermodynamics of Type-I Superconductors in Magnetic Fields
In a bulk superconductor, surface effects are unimportant; for now, we will assume that the order parameter is constant everywhere in the superconductor and that magnetic fields are completely expelled. In this case, the free energy per unit volume of the superconductor is
This is known as the condensation energy (per unit volume). We see that we can "save" energy by going into the superconducting state.
In the normal state, only the magnetic field terms are present, so that the free energy is
We may substitute in
to get
In the normal state, , so
The free energy per unit volume of the normal state is therefore
We see that, overall, we also "save" energy in the normal state. Which state we go into depends on which "saves" more energy. We may now define a field at which the "savings" are the same for both states; this is the (thermodynamic) critical field (sometimes also denoted ). Equating the free energies per unit volume of each state, we obtain
or, solving for ,
We see, therefore, that GL theory predicts a linear dependence of the critical field on the temperature. This is not what is observed experimentally, however. The dependence of the critical field on temperature in many real superconductors can, in fact, be modeled with the following empirical law:
We plot this relation below.
We see that, near , the dependence of the critical field on temperature does indeed follow the linear relation that we just derived. However, it deviates from said relation when we go far below . This is not surprising; the GL theory from which we obtained the linear relation is only valid near . In order to obtain a more accurate relation, we require a theory for the superconductor that is valid far below .
We may rewrite our dimensionless vector potential and magnetic field in terms of the critical field. We may write our expression for as
Our dimensionless vector potential is then
We may rewrite the definition of the magnetic field as
or
Magnetic Properties of a Type-I Superconductor
In the approximation stated above, we find that, in the superconducting state (the applied magnetic field is below ), the total magnetic field is completely expelled, while when the applied field is above . From the defining relation for the magnetization ,
we find that the magnitude of the magnetization increases linearly with, and points in the opposite direction to, , in the superconducting state, but is zero in the normal state. We plot these two relations below.
We will now demonstrate two consequences of the total expulsion of a magnetic field from a superconductor.
1) The total field is always tangential to the surface of a superconductor.
First, recall the Maxwell equation,
Let us now consider the boundary between a superconductor and a normal region:
We will find the flux of a magnetic field through the "pill box" shown above. Let the area of the circular surfaces be , and let us assume that the contribution from the "tube" part of the surface is negligible (we will assume that its height is small compared to the radius of the circular surfaces). Then the total flux may be written as
where and are the components of the magnetic field normal to the circular surfaces of the "pill box" in the normal and superconducting regions, respectively. The Maxwell equation stated above is equivalent to the statement that the total flux through a closed surface, such as the "pill box" we consider here, must be zero. Therefore,
However, we know that the superconductor completely expels magnetic fields, so that . Therefore, , thus proving that can only have tangential components.
2) As a direct consequence of (1), a type-I superconductor in an external magnetic field always carries an electrical current near its surface.
To show this, first recall the Maxwell equation (Ampere's Law in the case of static fields),
or, in integral form,
where is a surface with bounding curve , the line integral on the left is taken in the direction that would cause a right-handed screw to advance in the direction of the normal to the surface, and is the total current passing through the surface.
Let us now, once again, consider the boundary between a superconductor and a normal region and a rectangular contour drawn around the boundary:
In this case, because the magnetic field is zero in the superconducting region and because the magnetic field in the normal region is tangential to the surface of the superconductor, then, assuming that the lengths of segments 14 and 23 are small compared to that of segments 12 and 34. In this case, the left-hand side of the Maxwell equation becomes
where is the length of segment 12. The right-hand side, on the other hand, is
where is the surface current density (per unit length). This implies that
or, in vector form,
where is the normal to the surface pointing into the normal region. In the case depicted above, we see that points into the page or screen.
An Example: The Magnetic Field Around a Spherical Superconductor
These observations lead to interesting conclusions for superconductors with geometries more complex than a cylinder inside a magnetic field parallel to its axis. Consider, for example, a spherical superconductor, depicted below:
As we can see, the magnetic field near the equator is stronger than the applied field, while the field at the poles vanishes. This implies that the magnetic field near the equator may exceed even if the applied field is less than , simply due to the geometry of the sample. In fact, for a certain range of fields,
the sample will enter an intermediate state, in which superconducting and normal regions coexist. The above inequality holds for any geometry, in fact, and is known as the demagnetizing factor of the sample. Its value will depend on the exact geometry of the sample; we will now show that, for a sphere, . We will do so by solving Maxwell's equations for a spherical superconductor of radius in a uniform applied magnetic field . The boundary conditions for this problem are
for and
on the surface of the sphere. Outside the superconductor, the equations satisfied by are
and
The second equation implies that there are no current sources outside the superconductor. It also implies that we may write the magnetic field in terms of a scalar potential. We therefore write
Substituting this into the first equation, we get
which is just Laplace's equation. Our boundary conditions for are, in spherical coordinates,
and
on the surface. Laplace's equation in spherical coordinates is
Because our system has azimuthal symmetry, should be independent of . Therefore, and Laplace's equation becomes
Multiplying by , we get
We will now attempt to solve this equation by separation of variables. Let us try a solution of the form
Then
We see that we have an expression depending only on on one side and one depending only on on the other. The only way for this equation to be satisfied is if both equal a constant, which we will call . Let us first consider the equation for . This equation is
If we make the substitution, , into this equation, we get
We recognize this as the Legendre differential equation. The only physically interesting solutions to this equation occur when , in which case we find that is a Legendre polynomial,
The first few Legendre polynomials are , , and .
Now we will consider the equation for . If we take , then our differential equation for becomes
or
This is an Euler-Cauchy differential equation. Let us assume a power law dependence for ,
The equation becomes
The exponent must therefore satisfy
This equation has two possible solutions, and , so the general solution for the differential equation is
The general solution to the original partial differential equation is then a linear combination of all possible products ,
Since for all , we must set for all such values of . We will also set , so that
We now apply the boundary condition,
to obtain
By inspection, we find that for all . For , we have
Therefore, the solution for is
and thus is
In spherical coordinates, the gradient operator is given by
so
We recognize that , so that
We now want to find the point at which the magnetic field has the largest magnitude. The magnitude of this vector is given by
We see that the second term, which is proportional to , is clearly negative when . Therefore, we must make the size of this term as small as possible. This may be done by letting . For this value of , we have
This function is monotonically decreasing as we increase ; therefore, we choose the smallest possible value of , which is . This gives us
or . Therefore, the total magnetic field achieves its maximum magnitude at the equator of the sphere, where it is three halves the applied field. Therefore, if the applied field is larger than , the field at the equator would become larger than , which would destroy the sphere's superconductivity at that point. Therefore, the sphere enters an intermediate state when , so that the demagnetizing factor .
Superconductors of General Geometries
In general, the maximum magnetic field on the surface of a superconductor will be related to the applied field by
We will now list the values of for a few different geometries.
| Geometry | Demagnetizing factor |
| Cylinder with parallel to its axis | |
| Cylinder with perpendicular to its axis | |
| Sphere | |
| Infinite thin plate with perpendicular to the plate |
The sample will enter the intermediate state at the value of at which , which is
Therefore, the superconductor will be in the intermediate state when
We will now show plots of the magnetic field of a sphere at the equator and at the pole as a function of the applied field (for details on how to derive the dependence in the intermediate state, see P. G. DeGennes, Superconductivity of Metals and Alloys).
In the intermediate state, the energy per volume of both the normal and superconducting states is the same. Therefore, the energy per unit area of a "domain wall" will be the dominant contribution.
Surface Term of the Free Energy
The free energy in the reduced units can be written as
where
Using the following relations:
one has
Now let's consider the gradinet term:
Integration by part leads the 2nd term to the form:
where the 1st term needs to be evaluated on the surface where it vanishes by the boundary condition for an insulating interface. Hence the gradient term becomes
Assuming that and satisfy the GL equation, namely,
we have
and the free energy becomes
This is true at the saddle point. Now the free energy for the normal state and the superconducting state are given by
and
Therefore, the surface free energy of the interface is
As shown in the figures below, type-I superconductor (left) has positive wall energy while type-II superconductor (right) negative wall energy.
Free Energy of a Normal-Superconducting Interface
Now let's consider the free energy of a normal-superconducting interface. Recall the GL equations:
Assume that the interface is along y-z plane and . We can choose which implies the order parameter depends only on . Then the GL equation become
(*)
and
Note that we can choose to be real since the coefficients are real. Now let's manipulate Eq.(*):
Integrating we have
This integral can be further manipulated:
Thus, Eq.(*) becomes
or,
To determine the const., note that as , and , so
Therefore,
Consider the case where , that is, . The main contribution to the surface energy comes from the region where but .
Note that the minus sign is from the experimental setup. Further,
Requiring at gives Now we have
whose curve is shown in the figure. Moreover,
where
Hence one has
Below we show that given and satisfying the GL equation, the surface energy of the surface vanishes at :
(**)
Assume .
Choosing
then and the 2nd GL equation becomes
Insert this into Eq.(**):
Therefore, as expected.
In summary, for type-I superconductor (positive surface energy) and is uniform in the bulk and jumps at . On the other hand, for type-II superconductor (negative surface energy) and is not uniform in the bulk but grows continuously when crossing from above.
The "Landau-Level"-Like States above Hc and the Upper Critical Field Hc2
Now we have the surface free energy:
where
and
Assuming 2nd order phase transition and , then and :
Using the Landau gauge:
Recall
Let
then
Let
then
Recall for a harmonic oscillator we have
and
Comparison leads to
and the eigenvalues
The exponent is zero when
If and we have
For , , the bulk is preempted by the Meissner phase. On the other hand, , , the bulk undergoes a 2nd order phase transition into a mixed state in which normal state and superconducting state coexist.
Now let's look at the wavefunction at .
Let
where Note that
For we have
and the order parameter is of the form
Abrikosov Solution of the GL Equation for Type-II Superconductor near Hc2
Note. In this section we will drop the "tilde(~)" on relevant quantities and recover it when necessary.
Since the conditions along the entire superconductor are uniform, we seek a linear combination of solutions centered through equal intervals, namely,
or,
with
Consider the solution to GL equation at slightly less than .The 2nd GL equation gives
For the x-component, we have
where
Similarly, for the y-component we have
Note that
Therefore,
Now we have
or,
which implies
At points where , . So
Note that the correction (the 2nd term) comes from induced current. Furthermore,
Now let's consider the 1st GL equation:
which is solced by dropping the non-linear term and A and leads to Hc2.
To 0th oeder:
To 1st order:
Add them up, we have
Multiplying the whole equation by and integrating over the variable y leads to
where
The above equation has this (inhomogeneous) form:
Consider the homogeneous version of this equation:
The only way for the inhomogeneous equation to have a solution is if
Thus we need
Let
then the identity is satisfied.
Now, multiply both sides by and sum over N we have
Taking the spatial average results in
or, recovering the "tilde(~)",
where
is the famous Abrikosov parameter which does not depend on or the normalization of . It is easy to see that is always greater than or equal to 1:
Note that
Hence
The equality holds when .
Recall that the surface free energy is given by
In order to obtain the thermodynamic potential which when differentiated with respect to H gives B we need to subtract (which came from the normal term) from the above expression:
Note that for type-II superconductor, , the whole expression is negative. So, to lower the the free energy we need to minimize .
Knowing we can obtain by differentiating with respect to and hence obtain the magnetization which is measurable.
for .
which means the type-II superconductor behaves like a diamagnet.
Abrikosov Vortex States
Now let's follow the step of Abrikosov to derive the vortex structure in type-II superconductor.
where .
Thus
Minimize with respect to k we find that at minimum
where and
where is the Jacobi elliptic theta function. The vanishes at points:
and
Obviously, the zeros form a square lattice of spacing in reduced units.
Now consider the current lines:
The lines of constant current magnitude are determined by the following condition:
which means the current flows along the contours of .
However, the actual solution which minimizes is a triangular lattice for which the coefficients satisfy
and .
Going below Tc with the Saddle Point Approximation
So, previously all of this work has shown us the behaviour of a superconducting system near only. If we want to go into lower temperatures, we will have to make a careful saddle-point approximation, following Bardeen, Cooper, and Schrieffer (BCS). Once again, we can start from our microscopic 'toy' Hamiltonian, and gain useful information.
Recall that the partition function can be written,
Where
and
Previously, we used a cumulant expansion around to find the Ginzburg-Landau equations, along with the assumption that was small. Now, if we throw away this assumption, pray that fluctuations are small, and that there is only one saddle point, we will be able to successfully describe the superconducting state deep below by demanding:
Self-Consistency Equation
The solution of this functional derivative equation will give the value of at the saddle point (and also the self-consistency equation for this mean-field theory.)
To that end:
and, since
We arrive at
So that, from the saddle-point condition, we find the Self-Consistency Equation:
This contains the same information as the Ginzburg-Landau equations, but also more, as we can now go far below . Evaluation of this cam be done formally, but is difficult and not terribly enlightening. Instead, we will search for a solution in which <math\psi</math> is independent of and , similar to our solution near . In this case, we also expect that will be independent of and .
First, it is useful to write down the action in momentum and frequency space, before evaluating the correlator.
Start with
For the three terms in , we have:
The integral over all space give , and the integral over imaginary time gives a factor of , so that we find
Now, for the 2nd (pairing) term:
This time, the integral over real space gives , and the integral over imaginary time gives a factor of , so the 2nd term becomes:
The hermitian conjugate of the above (the 3rd term in ) gives
So that, for the entire , we have found:
Now, to evaluate the Gaussian integrals in the correlator, it is extremely beneficial to write like a matrix. To this end, we construct the so-called Nambu Spinors:
So now, we can write the BCS action as:
Now, we can examine the correlator we found on the right-hand-side of the self-consistency equation:
So, we need to write down a generic matrix for , and take element for our result. The gaussian integrals require that and for convergence. Using our technology from last semester, we can show that:
Now, we can easily write down the correlator:
This reshapes our consistency equation to:
Which has a trivial, solution, and far more interesting solution where
Note that this is only possible if !
-We will not get S-wave superconductivity for independent of
-In cuprates, changes sign with . It changes sign like D-wave.
-If is repulsive system does not like to make uniform gap!
-In Fe-Pnictides, pairing gaps on different Fermi surfaces have different signs, with repulsion.
Let us define
So
We can write this as a complex contour integral, with a series of pole along the imaginary axis.
since
There is no divergence as There are two poles, at
The contour can be deformed so that they exclude these two poles, and the integrand is tiny as The only contribution comes from the the loop around the two poles. For , the integrand falls off as , which, by Jordan's lemma,is fast enough for convergence.
So the integrand becomes
Solution of the Self-Consistency Equation
By using our usual trick of ,
we can convert the sum into an integral:
At this point, we can, if we wish, solve this equation on a computer, at any temperature
For , the RHS is always intersects the LHS , and we are guaranteed a solution.
As we raise temperature, log-divergence of integer gets cut-off. Finding T-dependence of the intercept gives T-dependence of
There can be an analytic solution as
Assuming that the density of states is smooth, and dominated by , we can write:
Now,
In typical systems, ! For example, in Al, while . So, we can safely assume that , which gives that:
at .
This actually lowers condensation energy more than ! It is also important to note, that since enters in a exponential, that the is completely flat as , showing that this result is completely non-perturbative. Note that is only exactly zero when is zero, so that no matter how small the interaction, we still have a superconducting state.
Happily, this result is also something we can compare to experimental results from tunneling measurements on suitable materials (S-wave superconductors). From the definition of :
By convention, the BCS results for twice this is compared to experiment.
| Element | Measured |
| Al | |
| Cd | |
| Nb | |
| Sn | |
Going between and
At zero-Temperature,
Now lets look at how it agrees with the Ginzburg-Landau theory near
At finite T,
in units of
Now. let us parametrize with
(Note at )
so
Or,
Now , which is very large compared to the energy scale we are working at, and so we can replace the upper limit in the integrals by . This will cause the first term in the LHS to vanish, since it falls faster than We get,
Since we expect , we can switch their order inside the logarithm:
We are now in a position to solve for near
Let
So the RHS is
Let us call . So
Now as , the integral clearly goes to zero
So the integral is
Where is the modified Bessel function of the 2nd kind.
As , and as
For small temperatures, the sum is dominated by the smallest n value. So approximately,
By noting that is small, we can manipulate the logarithm to get
Next,let us solve near analytically
Near
At . So,
Let us subtract from both sides
Now if we let , the reason of which has already been argued, we can solve the LHS exactly, and we get,
So we get
The next logical step is to expand the hyperbolic tangent
So RHS
This series converges, and we get,
Where is the order three Reimann Zeta function.
Condensation energy and T dependence of the thermodynamic field
Using the saddle point approximation
Then,
We recall that
Then,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(\Delta _{0})-F(0)=V\frac{\Delta _{0}}{\left | g \right |}-\frac{1}{\beta } {\sum_{\omega _{n}}^{}}{\sum_{k}^{}}ln (1+\frac{\Delta _{0}^{2}}{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}})}
Here, the first term is positive whereas the second term should be negative.
In order to calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F[\Delta ]} we note that:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F[\Delta ]=-\frac{1}{\beta }{\sum_{\omega _{n}}^{}}ln(1+\frac{\Delta ^{2}}{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\mathrm{d} F[\Delta ]}{\mathrm{d} \Delta }=-\frac{1}{\beta }{\sum_{\omega _{n}}^{}}\frac{1}{(1+\frac{\Delta ^{2}}{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}})}\times \frac{2\Delta }{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -(2\Delta )\frac{1}{\beta }{\sum_{\omega _{n}}^{}}\frac{1}{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}+\Delta ^{2}}}
Choosing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=i\omega _{n}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\mathrm{d} F[\Delta ]}{\mathrm{d}\Delta }= -(2\Delta )\frac{1}{\beta }{\sum_{\omega _{n}}^{}}\frac{1}{E_{k}^{2}-z^{2}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =(2\Delta ){\oint_{c}^{}}\frac{dz}{2\pi i}\frac{1}{e^{\beta z}+1}\frac{-1}{(z+E_{k})(z-E_{k})}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =(\Delta )(\frac{n_{F(E_{k})}}{E_{k}}+\frac{n_{F}(-E_{k})}{-E_{k}})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =(\Delta )(\frac{n_{F(E_{k})}}{E_{k}}-\frac{(1-n_{F}(E_{k}))}{E_{k}})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{\Delta }{E_{k}}(-1+2n_{F}(E_{k}))}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \int_{0}^{\Delta }d\Delta \frac{\mathrm{d}F }{\mathrm{d} \Delta }=\int d\Delta \frac{\Delta }{\sqrt{(\epsilon _{k}-\mu )^{2}+\Delta ^{2}}}(-1+2{\frac{1}{(e^{\frac{\sqrt{(\epsilon _{k}-\mu )^{2}+\Delta ^{2}}}{T}}+1)})}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\sqrt{(\epsilon _{k}-\mu )^{2}+\Delta ^{2}}\, +\, 4T\, ln\, [cosh\frac{(\epsilon _{k}-\mu )^{2}+\Delta ^{2}}{2T}]+const.}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \because F[0]= 0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore F[\Delta ]=-E_{k}+\left | \epsilon _{k}-\mu \right |-4T\, ln\, [\frac{1+e^{-\frac{E_{k}}{T}}}{1+e^\frac{-(\epsilon _{k}-\mu )}{T}}]}
Using the self consistency equation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\left | g \right |}=\int \frac{d^{3}k}{\left ( 2\pi \right )^{3}}\frac{tanh\frac{E_{k}}{2T}}{2E_{k}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore F[\Delta _{0}]-F[0]}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ={\sum_{k}^{}}(\frac{\Delta _{0}^{2}}{2E_{k}}-E_{k}+\left | \epsilon _{k}-\mu \right |-\frac{\Delta _{0}^{2}(1-tanh\frac{E_{k}}{2T})}{2E_{k}})-4T\, ln\, (\frac{1+e^{-\frac{E_{k}}{T}}}{1+e^{-\frac{(\epsilon _{k}-\mu )}{T}}}) }
When T= 0, only the 1st term survives.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow F[\Delta _{0}]-F[0]=-V\frac{N_{0}\Delta ^{2}}{2}}
Beyond saddle-point approximation, collective modes and response in the broken symmetry state
Recall we can write our partition function as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D\Delta^*D\Delta e^{-S_{eff}[\Delta]}}
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D(\Re e\Delta)D(\Im m\Delta)e^{-S_{eff}[\Re e\Delta,\Im m\Delta]}}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{eff}[\Delta]=\frac{1}{|g|}\int_0^\beta d\tau\int d^Dr\left[(\Re e\Delta(r,\tau))^2+(\Im m\Delta(r,\tau))^2\right]-\ln\left[\int D\psi^*D\psi e^{-S_0-S_{int}}\right]}
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} S_0&=\int_0^\beta d\tau\int d^Dr \psi^*(r,\tau)(\frac{\partial}{\partial\tau}+\epsilon_p-\mu)\psi(r,\tau)\\ S_{int}&=\int_0^\beta d\tau\int d^Dr(\Delta^*(r,\tau)\psi_\downarrow(r,\tau)\psi_{\uparrow}(r,\tau)+\Delta(r,\tau)\psi^*_\uparrow(r,\tau)\psi^*_{\downarrow}(r,\tau)) \end{align}}
We can rewrite the interaction term in the action as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{int}=\int_0^\beta d\tau\int d^Dr\left[\Re e(\Delta(r,\tau))(\psi_{\downarrow}\psi_{\uparrow}+\psi_{\uparrow}^*\psi_{\downarrow}^*)(r,\tau)+i*\Im m(\Delta(r,\tau))(\psi_{\uparrow}^*\psi_{\downarrow}^*-\psi_{\downarrow}\psi_{\uparrow})(r,\tau)\right]}
Consider now functional derivatives of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{eff}[\Delta]} :
The functional derivative of with is
Therefore, we have
Similarly
If we were to set the LHS of the above two equations to zero, we would obtain our self-consistency conditions.
The strategy is to take
where solves (1) and (2) with LHS set to zero and expand in powers of . So
Since by definition of we have
So only the 0th and 2nd order terms contribute. The 0th order term gave us the condensation energy, and the 2nd order term will give us information about collective modes (in the broken symmetry phase).
So
i.e.
Similarly,
And
If we evaluate these functional derivatives at the saddle point we have
where we take the saddle point solution to be purely real. Arranging the Grassman fields into the Nambu spinor we have:
where the Nambu spinor is defined as
So
where the Green's functions are 2*2 matrices,
Notice that this is a function of and . Let's call it . This will give rise to
Fourier transforming we find the contribution to
Similarly
Then
To proceed with the evaluation of 's, note that
where . After Fourier transform,
Consider now
and
Now, note that at ,
because the numerator vanishes for all and . Also note that by self-consistency condition
However,
This sum is slowly convergent. To evaluate it efficiently, we note that
So
where is Jacobi elliptic theta function. Then
where
Note that
as , i.e. as .
That is precisely the curvature of the new minimum in the Ginzburg-Landau free energy we found before. So, at 2nd order our effective action corresponds to the action for two real free bosons, and . At , mode is gapped (massive), but mode is not gapped (massless). Physically, corresponds to the fluctuations of the order parameter amplitude (because we chose to be real).
Recall our discussion from many-body course:
Amplitude fluctuations are not hydrodynamic modes since they do not correspond to either conserved or to broken symmetry variable. We have to extend our approach to higher order in to describe its (rapid) decay.
corresponds to fluctuations along the direction of the minimum of the double well potential, where there is no barrier. It corresponds to (part of) a "phase" mode.
To determine the kinematics (of our collective modes) we need to expand in powers of and . Our small expansion parameters are
and
(Obviously )
Start with : What we need is
The second term in the brackets:
Now, by Taylor expansion,
and near the Fermi level we have
Also note that after integrating over and , terms with odd power of and vanish. Keeping only terms of order and we have
The terms which we dropped are down by powers of and/or vanish assuming particle-hole symmetry.
Let's focus on . Then
So at :
in 3D and for a spherical FS
Next
Now, the second term of the integrand:
Therefore,
Again at ,
Finally,
Now, expanding:
When multiplied by and integrated over or summed over all terms vanish if we assume particle-hole symmetry and . That is because needs to be multiplied either by a term which is odd in and even in and in , or by a term which is odd in and as well as even in . But there is no such term to any order. That means that the coupling term is given by particle-hole symmetry breaking terms or terms down by . With such terms present, we expect it to be . Although, there is a term with
we have a massive propagating mode AND a massless propagating mode with velocity . Such a mode would have to show up in specific-heat for instance as a correction to but it does not. Rather, we have found a (thermodynamic) sound mode of a super-fluid (which is neutral), not superconductor which is charged.
Anderson-Higgs "mechanism"
In order to properly describe the collective modes of a (charged) superconductor, we must include the effects of long-range Coulomb repulsion. That means that in addition to including the short-range attraction we must include the long-range repulsion.
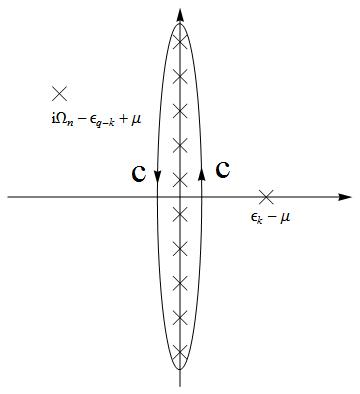
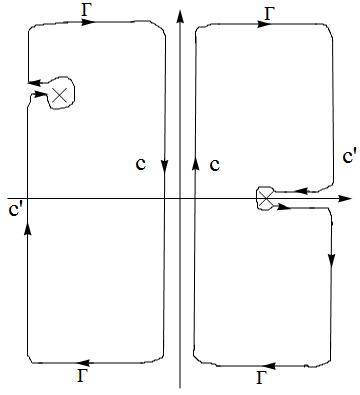
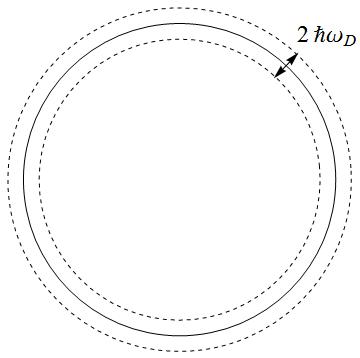
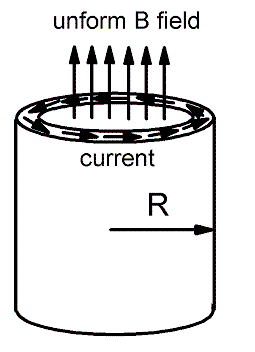
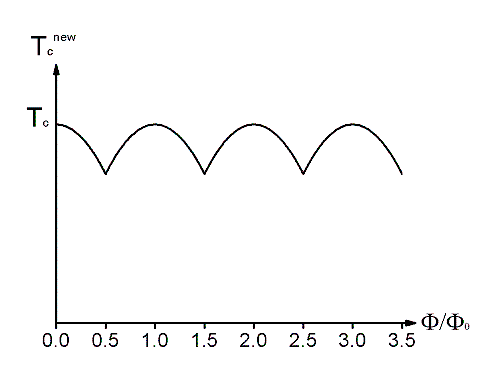





















![{\displaystyle S_{int}={\frac {L^{D}}{\beta ^{2}}}\sum _{\omega _{n},\Omega _{n}}\sum _{k,q}[\Delta _{q}^{*}(i\Omega _{n})\psi _{\downarrow }(i\Omega _{n}-i\omega _{n}),{\vec {q}}-{\vec {k}})\psi _{\uparrow }(i\omega _{n},k)+\Delta _{q}(i\Omega _{n})\psi _{\uparrow }^{\dagger }(i\omega _{n},k)\psi _{\downarrow }^{\dagger }(i\Omega _{n}-i\omega _{n}),{\vec {q}}-{\vec {k}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a85f99cd3f68852e145e1956e61803d8bfd87a8f)








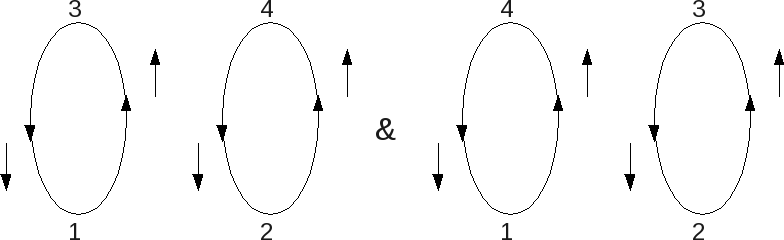
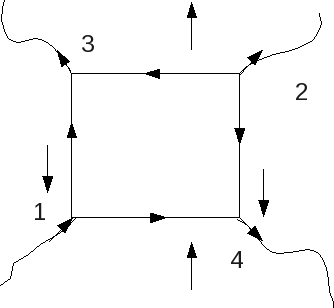
































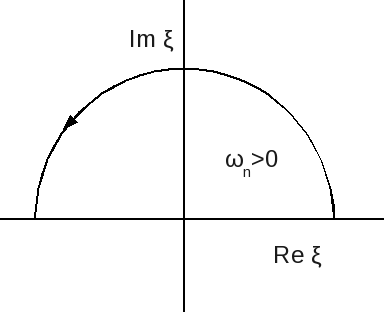










![{\displaystyle S_{eff}={\frac {1}{k_{B}T}}\sum _{r}\left[{\underset {A}{\underbrace {\left({\frac {1}{|g|}}-N(0)In\left[{\frac {2\hbar \omega _{D}e^{\gamma _{E}}}{\pi k_{B}T}}\right]\right)} }}|\Delta (r)|^{2}+N(0)\xi ^{2}(\nabla \Delta *(r)).(\nabla \Delta (r))+{\frac {1}{2}}{\underset {B}{\underbrace {\frac {7\zeta (3)N(0)}{8\pi ^{2}k_{B}^{2}T^{2}}} }}|\Delta (r)|^{4}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfd9a4f59d43962441a466c3c81366a812c961eb)
![{\displaystyle Z\sim Z_{0}e^{-S_{eff}[\Delta _{min}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aac519c60f52ae1cc5a38bc1133daadd5d100131)








![{\displaystyle S_{eff}[\Delta _{min}]={\frac {L^{D}}{k_{B}T}}\left(A\Delta _{min}^{2}+{\frac {1}{2}}B\Delta _{min}^{4}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faa3555544269331317298ea233f841c59c2b649)
![{\displaystyle T>T_{C};\quad S_{eff}[\Delta _{min}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da6f8326a3ef33e6e6a2a637a25be50396fecd1f)
![{\displaystyle T<T_{C};\quad S_{eff}[\Delta _{min}]=\left(A{\frac {-A}{B}}+{\frac {1}{2}}B{\frac {A^{2}}{B^{2}}}\right){\frac {L^{D}}{k_{B}T}}={\frac {-A^{2}}{2B}}{\frac {L^{D}}{k_{B}T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ee8046e319e073fcbd5c25fbac222fef8eb54a3)









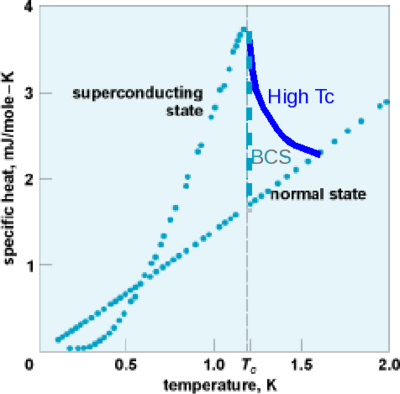



![{\displaystyle \delta F=\int d^{d}{\vec {r}}'\left[\alpha (T-T_{c})\Psi ({\vec {r}}')\,\delta \Psi ^{*}({\vec {r}}')+b|\Psi ({\vec {r}}')|^{2}\Psi ({\vec {r}}')\,\delta \Psi ^{*}({\vec {r}}')-{\frac {e}{mc}}{\vec {A}}({\vec {r}}')\cdot \left({\frac {\hbar }{i}}\nabla -{\frac {2e}{c}}{\vec {A}}({\vec {r}}')\right)\Psi ({\vec {r}}')\,\delta \Psi ^{*}({\vec {r}}')-{\frac {1}{2m}}{\frac {\hbar }{i}}\nabla \delta \Psi ^{*}({\vec {r}}')\cdot \left({\frac {\hbar }{i}}\nabla -{\frac {2e}{c}}{\vec {A}}({\vec {r}}')\right)\Psi ({\vec {r}}')\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e97d3c2adba853ec3d5fb808ecdcfd1246de576)
![{\displaystyle -{\frac {1}{2m}}\left\{{\frac {\hbar }{i}}\nabla \cdot \left[\left({\frac {\hbar }{i}}\nabla -{\frac {2e}{c}}{\vec {A}}({\vec {r}}')\right)\Psi ({\vec {r}}')\,\delta \Psi ^{*}({\vec {r}}')\right]-\left[{\frac {\hbar }{i}}\nabla \cdot \left({\frac {\hbar }{i}}\nabla -{\frac {2e}{c}}{\vec {A}}({\vec {r}}')\right)\Psi ({\vec {r}}')\right]\delta \Psi ^{*}({\vec {r}}')\right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f170f9f83d228f16fd6fd85d8a3bdc8468efa679)
![{\displaystyle \delta F=\int d^{d}{\vec {r}}'\left\{\alpha (T-T_{c})\Psi ({\vec {r}}')+b|\Psi ({\vec {r}}')|^{2}\Psi ({\vec {r}}')-{\frac {e}{mc}}{\vec {A}}({\vec {r}}')\cdot \left({\frac {\hbar }{i}}\nabla -{\frac {2e}{c}}{\vec {A}}({\vec {r}}')\right)\Psi ({\vec {r}}')+{\frac {1}{2m}}\left[{\frac {\hbar }{i}}\nabla \cdot \left({\frac {\hbar }{i}}\nabla -{\frac {2e}{c}}{\vec {A}}({\vec {r}}')\right)\Psi ({\vec {r}}')\right]\right\}\delta \Psi ^{*}({\vec {r}}').}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e883a52f49db26c167bd9a557cb2ed07e069f55)


![{\displaystyle \delta F_{SC}=i{\frac {e\hbar }{mc}}\int d^{d}{\vec {r}}'\left[\Psi ^{*}({\vec {r}}')\left(\nabla -i{\frac {2e}{\hbar c}}{\vec {A}}({\vec {r}}')\right)\Psi ({\vec {r}}')-\Psi ({\vec {r}}')\left(\nabla +i{\frac {2e}{\hbar c}}{\vec {A}}({\vec {r}}')\right)\Psi ^{*}({\vec {r}}')\right]\cdot \delta {\vec {A}}({\vec {r}}').}](https://wikimedia.org/api/rest_v1/media/math/render/svg/492f190737a40ec8709bc52689d02861c52c748e)











![{\displaystyle {\hat {n}}\cdot \left[\left(\Psi ^{*}{\frac {\hbar }{i}}\nabla \Psi -\Psi {\frac {\hbar }{i}}\nabla \Psi ^{*}\right)-{\frac {4e}{c}}|\Psi |^{2}{\vec {A}}\right]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81e95ecd7c999651340ab4a4a0f8f3237035573d)



![{\displaystyle {\frac {e\Psi _{0}^{2}}{mc}}\left(\psi ^{\ast }{\frac {\hbar }{i}}\nabla \psi -\psi {\frac {\hbar }{i}}\nabla \psi ^{\ast }\right)-{\frac {4e^{2}\Psi _{0}^{2}}{mc^{2}}}\left|\psi \right|^{2}{\vec {A}}={\frac {1}{4\pi }}\nabla \times [\nabla \times ({\vec {A}}-{\vec {A}}_{0})],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0301db5012e0400a5eb35796697d241325cb145b)






![{\displaystyle {\frac {4\pi e\lambda \Psi _{0}^{2}}{mc}}\left(\psi ^{\ast }{\frac {\hbar }{i}}{\tilde {\nabla }}\psi -\psi {\frac {\hbar }{i}}{\tilde {\nabla }}\psi ^{\ast }\right)-\left|\psi \right|^{2}{\vec {A}}={\tilde {\nabla }}\times [{\tilde {\nabla }}\times ({\vec {A}}-{\vec {A}}_{0})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdd17556c0ef78f0032d1948f5e50f4d58076c28)



![{\displaystyle {\frac {1}{2\kappa }}\left(\psi ^{\ast }{\frac {\tilde {\nabla }}{i}}\psi -\psi {\frac {\tilde {\nabla }}{i}}\psi ^{\ast }\right)-\left|\psi \right|^{2}{\vec {A}}={\tilde {\nabla }}\times [{\tilde {\nabla }}\times ({\tilde {A}}-{\tilde {A}}_{0})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4050f4433ddf9d186140034a351c0541c8371308)

















![{\displaystyle \kappa ={\sqrt {\frac {18\pi ^{3}}{7\zeta (3)}}}{\frac {k_{B}T_{c}}{{\sqrt {mc^{2}}}{\sqrt {\alpha }}{\sqrt {2E_{F}}}}}\left({\frac {c}{v_{F}}}\right)^{3/2}=8\times 10^{-6}\cdot {\frac {T_{c}\,[{\text{K}}]}{\sqrt {E_{F}\,[{\text{eV}}]}}}\left({\frac {c}{v_{F}}}\right)^{3/2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad3bf53332107b6b1a161e37031716a99a831135)

![{\displaystyle \kappa =(0.04-1.3)\cdot {\frac {T_{c}\,[{\text{K}}]}{\sqrt {E_{F}\,[{\text{eV}}]}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/160e3943a348fbae34e87a34793d49e9be0962be)

































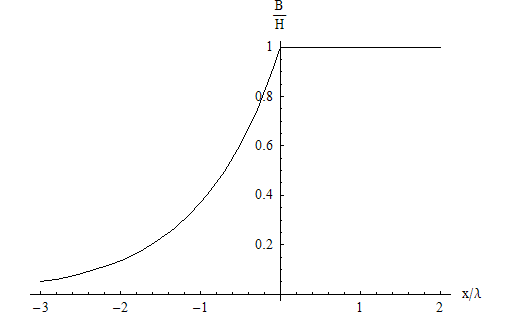

![{\displaystyle F_{n}=\int d^{d}{\vec {r}}\,\left[{\frac {1}{8\pi }}(\nabla \times {\vec {A}})^{2}-{\frac {1}{c}}{\vec {J}}_{\text{ext}}\cdot {\vec {A}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1af934e36d17a02944664685cbcb9663302bf95f)

![{\displaystyle F_{n}=\int d^{d}{\vec {r}}\,\left[{\frac {1}{8\pi }}(\nabla \times {\vec {A}})^{2}-{\frac {1}{4\pi }}(\nabla \times {\vec {H}})\cdot {\vec {A}}\right]=\int d^{d}{\vec {r}}\,\left[{\frac {1}{8\pi }}(\nabla \times {\vec {A}})^{2}-{\frac {1}{4\pi }}(\nabla \times {\vec {A}})\cdot {\vec {H}}\right]=\int d^{d}{\vec {r}}\,\left[{\frac {1}{8\pi }}B^{2}-{\frac {1}{4\pi }}{\vec {B}}\cdot {\vec {H}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bb6a904177e6b7b53134c0752e24104fd4f921f)






![{\displaystyle H_{c}(T)=H_{c}(0)\left[1-\left({\frac {T}{T_{c}}}\right)^{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7573d42b3df8ed058dcac90d04ccf84c69eb069e)
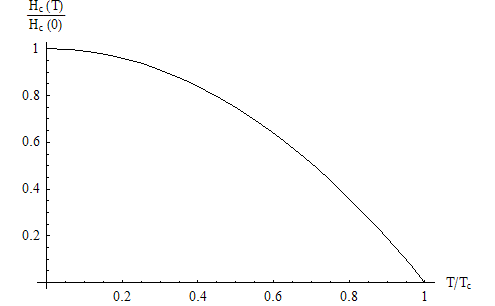






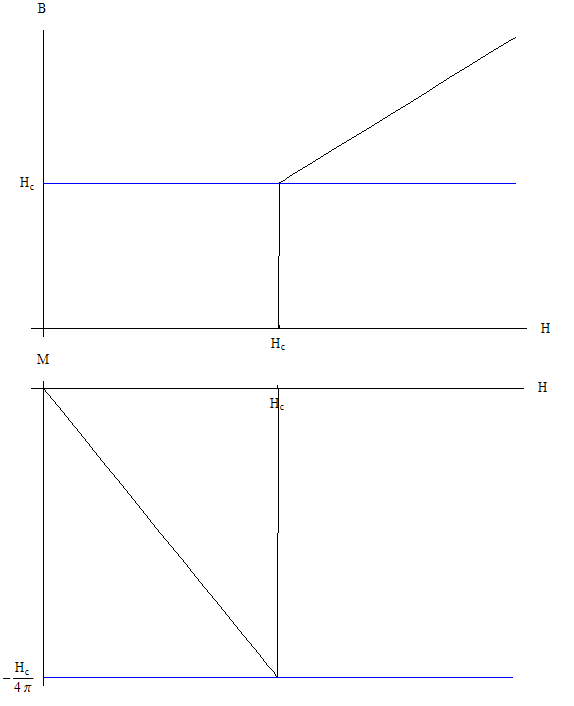

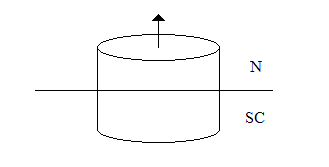












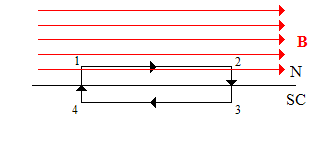






































![{\displaystyle {\frac {d}{dx}}\left[(1-x^{2}){\frac {d\chi }{dx}}\right]=\lambda \chi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c47b64aec978f02fcdfc0bf325317bad2659ece)


































![{\displaystyle {\vec {B}}=\left[1-\left({\frac {R}{r}}\right)^{3}\right]H\cos {\theta }{\hat {r}}-\left[1+{\tfrac {1}{2}}\left({\frac {R}{r}}\right)^{3}\right]H\sin {\theta }{\hat {\theta }}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b1c9032c54b63f36e2583ce16de490766a15a2f)
![{\displaystyle |{\vec {B}}|^{2}=H^{2}\left[1+{\tfrac {1}{2}}\left({\frac {R}{r}}\right)^{3}\right]^{2}+3\left({\frac {R}{r}}\right)^{3}\left[{\tfrac {1}{4}}\left({\frac {R}{r}}\right)^{3}-1\right]\cos ^{2}{\theta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50c35ae1e60a782553d399bf31c6385701fa19bb)



![{\displaystyle |{\vec {B}}|^{2}=H^{2}\left[1+{\tfrac {1}{2}}\left({\frac {R}{r}}\right)^{3}\right]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/802f03b6eff8286bbde9c98f2db1f1dd2c63fb2b)














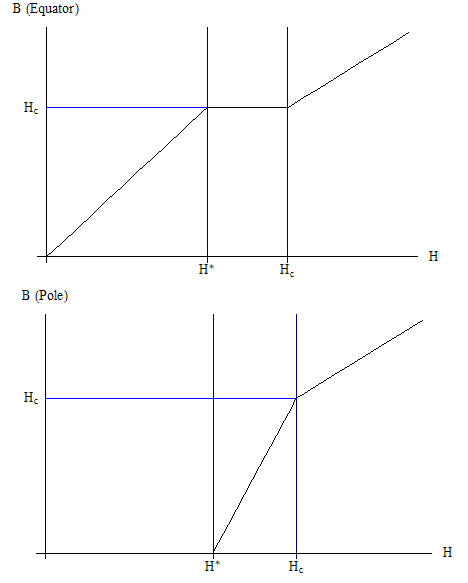
![{\displaystyle F=\int d^{3}r\,\left[\alpha (T-T_{c})|\Psi |^{2}+{\frac {b}{2}}|\Psi |^{4}+{\frac {\hbar ^{2}}{2m}}|(\nabla -{\frac {2ei}{\hbar c}}{\vec {A}})\Psi |^{2}+{\frac {1}{8\pi }}(\nabla \times {\vec {A}})^{2}-{\frac {1}{4\pi }}{\vec {H}}\cdot {\vec {B}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2198c9477c683173fa027f7fe82ad86aa485cda5)
![{\displaystyle =\lambda ^{D}\int d^{D}{\tilde {r}}\,\left[\alpha (T-T_{c})|\Psi _{o}|^{2}|\psi |^{2}+{\frac {b}{2}}|\Psi _{o}|^{4}|\psi |^{4}+{\frac {\hbar ^{2}}{2m_{GL}}}|\Psi _{o}|^{2}|({\frac {1}{\lambda }}{\tilde {\nabla }}-{\frac {2ei}{\hbar c}}{\sqrt {2}}\lambda H_{c}{\tilde {A}})\psi |^{2}+{\frac {1}{8\pi \lambda ^{2}}}({\sqrt {2}}\lambda H_{c})^{2}({\tilde {\nabla }}\times {\tilde {A}})^{2}-{\frac {2\lambda ^{2}H_{c}^{2}}{4\pi \lambda ^{2}}}{\tilde {H}}\cdot {\tilde {B}}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6717f0ff81b2b80cfd75235fa88a7efe3cf9b720)




![{\displaystyle F={\frac {\lambda ^{D}H_{c}^{2}}{4\pi }}\int d^{D}{\tilde {r}}\,\left[-|\psi |^{2}+{\frac {1}{2}}|\psi |^{4}+|({\frac {1}{\kappa }}{\frac {\tilde {\nabla }}{i}}-{\tilde {A}})\psi |^{2}+{\tilde {B}}^{2}-2{\tilde {H}}\cdot {\tilde {B}}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b8b353146cebf9cbed8f5667a28d3846f23594b)
![{\displaystyle |({\frac {1}{\kappa }}{\frac {\tilde {\nabla }}{i}}-{\tilde {A}})\psi |^{2}=\,\left[({\frac {-1}{\kappa }}{\frac {\tilde {\nabla }}{i}}-{\tilde {A}})\psi ^{*}\,\right]\,\left[({\frac {1}{\kappa }}{\frac {\tilde {\nabla }}{i}}-{\tilde {A}})\psi \,\right]=(-{\tilde {A}}\psi ^{*})({\frac {1}{\kappa }}{\frac {\tilde {\nabla }}{i}}-{\tilde {A}})\psi -({\frac {1}{\kappa }}{\frac {\tilde {\nabla }}{i}}\psi ^{*})({\frac {1}{\kappa }}{\frac {\tilde {\nabla }}{i}}-{\tilde {A}})\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ab14e87e781bf145c05e56e9ac30eb8e76e786f)





![{\displaystyle F={\frac {\lambda ^{D}H_{c}^{2}}{4\pi }}\int d^{D}{\tilde {r}}\,\left[-{\frac {1}{2}}|\psi |^{4}+{\tilde {B}}^{2}-2{\tilde {H}}\cdot {\tilde {B}}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b6bd56458c2a8c233e33119bf728604aa8480d8)
![{\displaystyle F_{n}={\frac {\lambda ^{D}H_{c}^{2}}{4\pi }}\int d^{D}{\tilde {r}}\,\left[-{\tilde {H}}^{2}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/136f2203d240c93e5693ecd788b9a5cf7a31bd22)
![{\displaystyle F_{s}={\frac {\lambda ^{D}H_{c}^{2}}{4\pi }}\int d^{D}{\tilde {r}}\,\left[-{\frac {1}{2}}|\psi |^{4}+{\tilde {B}}^{2}-2{\tilde {B}}\cdot {\tilde {H}}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7db654a11aa703212ffe9a2ba5e6fd474ce866)
![{\displaystyle F_{s}-F_{n}={\frac {\lambda ^{D}H_{c}^{2}}{4\pi }}\int d^{D}{\tilde {r}}\,\left[-{\frac {1}{2}}|\psi |^{4}+{\tilde {B}}^{2}-2{\tilde {B}}\cdot {\tilde {H}}+{\tilde {H}}^{2}\,\right]={\frac {\lambda ^{D}H_{c}^{2}}{4\pi }}\int d^{D}{\tilde {r}}\,\left[-{\frac {1}{2}}|\psi |^{4}+({\tilde {B}}-{\tilde {H}})^{2}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/048ae27a0522fd09fc2ca1c333957b6e6ec50ffd)
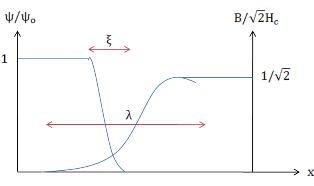
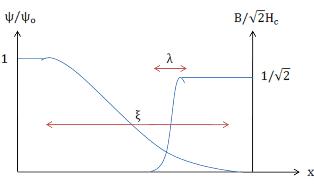





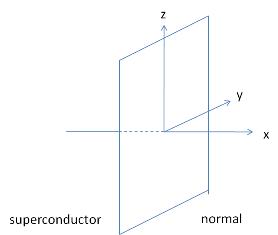






![{\displaystyle \int d{\tilde {x}}{\tilde {A}}_{y}^{2}{\frac {d}{d{\tilde {x}}}}\psi ^{2}=\int d{\tilde {x}}\,\left[{\frac {d}{d{\tilde {x}}}}({\tilde {A}}_{y}^{2}\psi ^{2})-{\frac {d{\tilde {A}}_{y}^{2}}{d{\tilde {x}}}}\psi ^{2}\,\right]={\tilde {A}}_{y}^{2}\psi ^{2}-2\int d{\tilde {x}}{\tilde {A}}_{y}{\frac {d{\tilde {A}}_{y}}{d{\tilde {x}}}}\psi ^{2}={\tilde {A}}_{y}^{2}\psi ^{2}-2\int d{\tilde {x}}{\frac {d{\tilde {A}}_{y}}{d{\tilde {x}}}}{\frac {d^{2}{\tilde {A}}_{y}}{d{\tilde {x}}^{2}}}={\tilde {A}}_{y}^{2}\psi ^{2}-\int d{\tilde {x}}{\frac {d}{d{\tilde {x}}}}({\frac {d{\tilde {A}}_{y}}{d{\tilde {x}}}})^{2}={\tilde {A}}_{y}^{2}\psi ^{2}-({\frac {d{\tilde {A}}_{y}}{d{\tilde {x}}}})^{2}=const.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d29b10f07f2867d6b445356cbc46b32ae2d0c59d)

















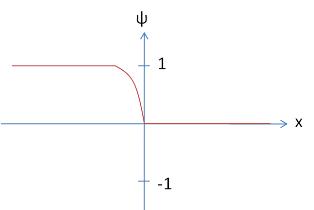






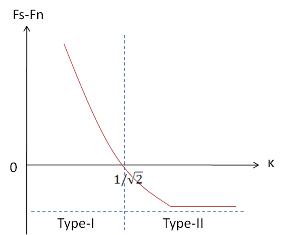




![{\displaystyle F_{s}-F_{n}={\frac {H_{c}^{2}}{4\pi }}L^{2}\lambda \int d{\tilde {x}}\,\left[({\tilde {B}}-{\tilde {H}})^{2}-{\frac {1}{2}}\psi ^{4}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96db5ec53fbd8e6983f8da1b886d87e338b3064c)

![{\displaystyle F_{s}-F_{n}={\frac {H_{c}^{2}}{4\pi }}L^{2}\lambda \int d{\tilde {x}}\,\left[({\frac {d{\tilde {A}}_{y}}{d{\tilde {x}}}}-{\frac {1}{\sqrt {2}}})^{2}-{\frac {1}{2}}\psi ^{4}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d53219b72659f859c266ee39d5bb3ae98d3dc40)









![{\displaystyle F_{s}-F_{n}={\frac {H_{c}^{2}}{4\pi }}\lambda ^{3}\int d^{3}{\tilde {r}}\,\left[-|\psi |^{2}+|({\frac {1}{\kappa }}{\frac {\tilde {\nabla }}{i}}-{\tilde {A}})^{2}\psi |^{2}+{\frac {1}{2}}|\psi |^{4}+({\tilde {B}}-{\tilde {H}})^{2}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0978c594570d557d750dff95d0c1788c36261664)




![{\displaystyle F_{s}-F_{n}={\frac {H_{c}^{2}}{4\pi }}\lambda ^{3}\int d^{3}{\tilde {r}}\,\left[-|\psi |^{2}+|({\frac {1}{\kappa }}{\frac {\tilde {\nabla }}{i}}-{\tilde {A}})^{2}\psi |^{2}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eb0ae3e321bd36cf3bc045741f4d0a96c5331f4)





![{\displaystyle e^{ik_{z}{\tilde {z}}}e^{ik{\tilde {y}}}\,\left[-{\frac {1}{\kappa ^{2}}}{\frac {d^{2}}{d{\tilde {x}}^{2}}}\Phi +({\frac {k}{\kappa }}-{\tilde {H}}{\tilde {x}})^{2}\Phi +{\frac {k_{z}^{2}}{\kappa ^{2}}}\Phi -\Phi \,\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17ad0281b9c2ded7f8216fba3f80fe4fd34a6c75)


















![{\displaystyle [a,a^{+}]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/565f4ef6ba616dcd0206d07987de31e877e1b5ce)















![{\displaystyle ={\frac {-i}{2\kappa }}\Sigma _{n,m}C_{n}^{*}C_{m}e^{-ik(n-m)y}\,\left[\phi _{n}(x){\frac {\partial }{\partial x}}\phi _{m}(x)-\phi _{m}(x){\frac {\partial }{\partial x}}\phi _{n}(x)\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a373be3e0905b62a726018941604ef059a6bffc)
![{\displaystyle [...]=-\kappa ^{2}(x-{\frac {km}{\kappa ^{2}}})\phi _{n}(x)\phi _{m}(x)+\kappa ^{2}(x-{\frac {kn}{\kappa ^{2}}})\phi _{n}(x)\phi _{m}(x)=k(m-n)\phi _{n}(x)\phi _{m}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2cae7da8e6f35c02e1bc9d13ca7ce68fa2bf591)
![{\displaystyle {\frac {\partial B_{z}}{\partial y}}={\frac {-i}{2\kappa }}\Sigma _{n,m}C_{n}^{*}C_{m}e^{-ik(n-my)}k(m-n)\phi _{n}(x)\phi _{m}(x)={\frac {\partial }{\partial y}}\,\left[{\frac {1}{2\kappa }}\Sigma _{n,m}C_{n}^{*}C_{m}e^{-ik(n-m)y}\phi _{n}(x)\phi _{m}(y)\,\right]={\frac {\partial }{\partial y}}\,\left[{\frac {-1}{2\kappa }}|\psi ^{(0)}|^{2}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbc9c67686890a8e185480bdfd742de08a625305)
![{\displaystyle -{\frac {\partial B_{z}}{\partial x}}={\frac {-i}{2\kappa }}\Sigma _{n,m}\,\left[C_{n}^{*}e^{-ikny}\phi _{n}(x)ikme^{ikmy}\phi _{m}(x)C_{m}+C_{n}^{*}ikne^{-ikny}\phi _{n}(x)e^{ikmy}\phi _{m}C_{m}\,\right]-\kappa x|\psi ^{(0)}|^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3ad995a96b58b7b43bfca6f2a8ca4da5a1c4233)
![{\displaystyle ={\frac {1}{2\kappa }}\Sigma _{n,m}\,\left[k(n+m)-2\kappa ^{2}x\,\right]C_{n}^{*}C_{m}e^{-ik(n-m)y}\phi _{m}(x)\phi _{n}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85c007a058a0d7283e088f2a8504f175bc9dbf82)
![{\displaystyle {\frac {\partial }{\partial x}}\,\left[\phi _{m}(x)\phi _{m}(x)\,\right]=\,\left[-\kappa ^{2}(x-{\frac {km}{\kappa ^{2}}})-\kappa ^{2}(x-{\frac {kn}{\kappa ^{2}}})\,\right]\phi _{m}(x)\phi _{n}(x)=-\,\left[2\kappa ^{2}x-k(m+n)\,\right]\phi _{m}(x)\phi _{n}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d27c09218499ebae64c0a7781056489265dd5ced)
![{\displaystyle -{\frac {\partial B_{z}}{\partial x}}={\frac {\partial }{\partial x}}\,\left[{\frac {1}{2\kappa }}|\psi ^{(0)}|^{2}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3a5655c772f7a390d4f05fa37e4ec83c8cf0d53)
![{\displaystyle {\frac {\partial B_{z}}{\partial y}}=-{\frac {\partial }{\partial y}}\,\left[{\frac {1}{2\kappa }}|\psi ^{(0)}|^{2}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ae24b59fd440dec92e2534b83a1ed2db3d03ff6)
![{\displaystyle {\frac {\partial B_{z}}{\partial x}}=-{\frac {\partial }{\partial x}}\,\left[{\frac {1}{2\kappa }}|\psi ^{(0)}|^{2}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec48cf1d2aad16f12fbed15fea173a4f2469fc6a)















![{\displaystyle \,\left[{\frac {-1}{\kappa ^{2}}}{\frac {\partial ^{2}}{\partial x^{2}}}+({\frac {1}{\kappa }}{\frac {1}{i}}{\frac {\partial }{\partial y}}-\kappa x)^{2}\,\right]\Sigma _{n}e^{ikny}\psi _{n}^{(1)}(x)=\Sigma _{n}e^{ikny}\,\left[{\frac {-1}{\kappa ^{2}}}{\frac {\partial ^{2}}{\partial x^{2}}}+({\frac {kn}{\kappa }}-\kappa x)^{2}\,\right]\psi _{n}^{(1)}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2530c314b04b1e0c23800f24a79213a80691268f)
![{\displaystyle -({\frac {1}{\kappa }}{\frac {1}{i}}{\frac {\partial }{\partial y}}-\kappa x)\,\left[(H-\kappa )x-{\frac {1}{2\kappa }}\int ^{x}|\psi ^{(0)}|^{2}\,\right]\Sigma _{n}e^{ikny}\phi _{n}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb248fbe3744a6f9bd96c82015e2686147b96a32)





![{\displaystyle \Sigma _{n}e^{ikny}\,\left[{\frac {-1}{\kappa ^{2}}}{\frac {\partial ^{2}}{\partial x^{2}}}+({\frac {kn}{\kappa }}-\kappa x)^{2}+1\,\right]\psi ^{(1)}=\Sigma _{n}e^{ikny}C_{n}2x(H-\kappa )({\frac {kn}{\kappa }}-\kappa x)\phi _{n}(x)-\Sigma _{n,m,p}e^{ik(n-m+p)y}C_{n}C_{m}^{*}C_{p}\,\left[({\frac {(2n-m+p)k}{\kappa }}-2\kappa ){\frac {1}{2\kappa }}\phi _{n}(x)\int ^{x}dx'\phi (x')\phi (x')+\phi _{n}(x)\phi _{m}(x)\phi _{p}(x)\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f17696c7d3bf0471563200a71f5c44b38705a8c)

![{\displaystyle \,\left[{\frac {-1}{\kappa ^{2}}}{\frac {\partial ^{2}}{\partial x^{2}}}+({\frac {kN}{\kappa }}-\kappa )^{2}-1\,\right]\psi _{N}^{(1)}(x)=C_{N}2x(H-\kappa )({\frac {kx}{\kappa }}-\kappa x)\phi _{N}(x)-\Sigma _{m,p}C_{N+m-p}C_{m}^{*}C_{p}\,\left[({\frac {k}{\kappa }}(2N+2m-2p-m+p)-2\kappa x){\frac {1}{2\kappa }}\phi _{N+m-p}(x)\int ^{x}dx'\phi _{m}(x')\phi _{p}(x')+\phi _{N+m-p}(x)\phi _{m}(x)\phi _{p}(x)\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d30318aae7f887de30d24483b96d067fe5eeb5b8)



![{\displaystyle \,\left[{\frac {-1}{\kappa ^{2}}}{\frac {\partial ^{2}}{\partial x^{2}}}+({\frac {kN}{\kappa }}-\kappa x)^{2}-1\,\right]\chi (x)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b549f1d49b1eabfbc9a325d9aa3ae21b10675b4f)

![{\displaystyle 0=C_{N}2(H-\kappa )\int _{-\infty }^{\infty }dxx({\frac {kN}{\kappa }}-\kappa x)\phi _{N}^{2}(x)-\Sigma _{m,p}C_{N-p+m}C_{m}^{*}C_{p}\,\left[\int _{-\infty }^{\infty }dx\phi _{N}(x)({\frac {k}{2\kappa ^{2}}}(2N+m-p)-x)\phi _{N+m-p}(x)\int ^{x}dx'\phi _{m}(x')\phi _{p}(x')+\int _{-\infty }^{\infty }dx\phi _{N}(x)\phi _{N+m-p}(x)\phi _{m}(x)\phi _{p}(x)\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5090c0dde27d93277310e8a6c41832f81f724bfb)


















![{\displaystyle F_{s}-F_{n}={\frac {H_{c}^{2}}{4\pi }}\lambda ^{3}\int d^{3}{\tilde {r}}\,\left[({\tilde {B}}-{\tilde {H}})^{2}-{\frac {1}{2}}|\psi |^{4}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c12bb8d2c653a5d8f51d7836cca848fed0b5bdb)

![{\displaystyle \Omega ={\frac {H_{c}^{2}}{4\pi }}\lambda ^{3}\int d^{3}{\tilde {r}}\,\left[({\tilde {B}}-{\tilde {H}})^{2}-{\tilde {H}}^{2}-{\frac {1}{2}}|\psi |^{4}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/582634a14c5ff20624ff433970314d451a195e77)
![{\displaystyle ={\frac {H_{c}^{2}}{4\pi }}L^{3}\,\left[{\frac {1}{4\kappa ^{2}}}<|\psi |^{4}>-{\tilde {H}}^{2}-{\frac {1}{2}}<|\psi |^{4}>\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95fec3dfd6bdfc0a1ac7eed2b5b41777b0e1e82c)
![{\displaystyle ={\frac {H_{c}^{2}}{8\pi }}L^{3}\,\left[{\frac {1-2\kappa ^{2}}{2\kappa ^{2}}}<|\psi |^{4}>-2{\tilde {H}}^{2}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c73565def89d4eec2b7513ebed47daeb986a9a0)
![{\displaystyle ={\frac {H_{c}^{2}}{8\pi }}L^{3}\,\left[{\frac {2}{1-2\kappa ^{2}}}{\frac {1}{\beta _{A}}}({\tilde {H}}-\kappa )^{2}-2{\tilde {H}}^{2}\,\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04a40c2d6c67b1e9c9a9d9ca636caac762e711f0)




![{\displaystyle B=-{\frac {H_{c}}{2{\sqrt {2}}}}4({\frac {1}{\beta _{A}}}{\frac {{\tilde {H}}-\kappa }{1-2\kappa ^{2}}}-{\tilde {H}})=-{\frac {2H_{c}}{\sqrt {2}}}\,\left[{\frac {1}{\beta _{A}}}{\frac {1}{1-2\kappa ^{2}}}({\frac {H}{{\sqrt {2}}H_{c}}}-{\frac {H_{c2}}{{\sqrt {2}}H_{c}}})-{\frac {H}{{\sqrt {2}}H_{c}}}\,\right]={\frac {1}{\beta _{A}}}{\frac {1}{1-2\kappa ^{2}}}(H-H_{c2})+H\leq H}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed5f6b892ef87f6f3a99f5a224caf4164980b06c)
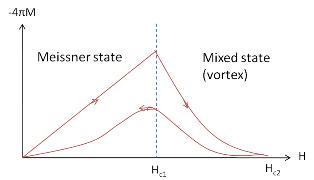
































![{\displaystyle \mathbb {Z} =\int {d\Delta ^{*}d\Delta }\left[\int {D\psi ^{*}D\psi \ e^{-S_{BCS}-S_{\Delta }}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f51a0d63575ad7eb530978e6614ec49b8f027fbb)

![{\displaystyle S_{BCS}=S_{0}+S_{int}\;\;{\text{where}}\;\;S_{0}=\int _{0}^{\beta }{d\tau }\int {d^{3}r}\left[\psi _{\sigma }^{*}({\vec {r}},\tau )\left({\frac {\partial }{\partial \tau }}+\epsilon _{p}-\mu \right)\psi _{\sigma }({\vec {r}},\tau )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1457eaf66dc9e3e578322ad48ad1640c82448372)
![{\displaystyle {\text{and}}\;\;S_{int}=\int _{0}^{\beta }{d\tau }\int {d^{3}r}\left[\Delta ^{*}({\vec {r}},\tau )\psi _{\downarrow }({\vec {r}},\tau )\psi _{\uparrow }({\vec {r}},\tau )+\Delta ({\vec {r}},\tau )\psi _{\downarrow }({\vec {r}},\tau )\psi _{\uparrow }({\vec {r}}.\tau )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f781421f5f363ad0528212168f5dc4c80052ad5)
![{\displaystyle {\frac {\partial S_{eff}[\Delta ]}{\partial \Delta *}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9dd5dfcc622b0bb4e79bb3aaddc5d2f6499a988)

![{\displaystyle S_{eff}[\Delta ]=S_{\Delta }-\ln \left(\int {D\psi D\psi ^{*}}\;\;e^{-S_{BCS}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3d1bf83d31213f21ab75991df2b8a87a6f6adac)

![{\displaystyle {\frac {\partial \left[-\ln \left(\int {D\psi D\psi ^{*}}\;\;e^{-S_{BCS}}\right)\right]}{\partial \Delta ^{*}({\vec {r}},\tau )}}={\frac {-1}{\int {D\psi D\psi ^{*}}\;\;e^{-S_{BCS}}}}\int {D\psi D\psi *}{\frac {\partial e^{-S_{BCS}}}{\partial \Delta ^{*}}}={\frac {\int {D\psi D\psi ^{*}}\;\;e^{-S_{BCS}}{\frac {\partial S_{BCS}}{\partial \Delta ^{*}}}}{\int {D\psi D\psi ^{*}}\;\;e^{-S_{BCS}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eccd2ac7e6e8bfb4f969dd2446f44cc75e15c5cc)

![{\displaystyle {\frac {\partial \left[-\ln \left(\int {D\psi D\psi ^{*}}\;\;e^{-S_{BCS}}\right)\right]}{\partial \Delta ^{*}({\vec {r}},\tau )}}={\frac {\int {D\psi D\psi ^{*}}\;\;e^{-S_{BCS}}\psi _{\downarrow }({\vec {r}},\tau )\psi _{\uparrow }({\vec {r}},\tau )}{\int {D\psi D\psi ^{*}}\;\;e^{-S_{BCS}}}}=\langle \psi _{\downarrow }({\vec {r}},\tau )\psi _{\uparrow }({\vec {r}},\tau )\rangle _{BCS}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/114ee21487afc6eb861ced705dc43d2182e92e6a)




![{\displaystyle S_{0}=\int _{0}^{\beta }{d\tau }\int {d^{3}r}\left[\psi _{\sigma }^{*}({\vec {r}},\tau )\left({\frac {\partial }{\partial \tau }}+\epsilon -\mu \right)\psi _{\sigma }({\vec {r}},\tau )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/003d33e87a4cdde801f175fa6b41c26947df8c7f)









![{\displaystyle S_{BCS}={\frac {1}{\beta }}\sum _{\omega _{n}}\sum _{\vec {k}}\left[\left(i\omega _{n}+\epsilon _{-{\vec {k}}}-\mu \right)\psi _{\uparrow ,-{\vec {k}}}^{*}(-i\omega _{n})\psi _{\uparrow ,-{\vec {k}}}(-i\omega _{n})+\left(-i\omega _{n}+\epsilon _{\vec {k}}-\mu \right)\psi _{\downarrow ,{\vec {k}}}^{*}(i\omega _{n})\psi _{\downarrow ,{\vec {k}}}(i\omega _{n})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16473cfae4c8b16a37802b2a75214151113941a9)
![{\displaystyle +{\frac {1}{\beta }}\sum _{\omega _{n}}\sum _{\vec {k}}\left[\Delta ^{*}\psi _{\downarrow ,{\vec {k}}}(i\omega _{n})\psi _{\uparrow ,-{\vec {k}}}(-i\omega _{n})+\Delta \psi _{\uparrow ,-{\vec {k}}}^{*}(-i\omega _{n})\psi _{\downarrow ,{\vec {k}}}^{*}(i\omega _{n})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/044d35aa4a55c834887d5b64daf73b1b879d3651)









![{\displaystyle \langle \Psi _{\vec {k}}^{*}(i\omega _{n})_{\mu }\Psi _{-{\vec {k'}}}(-i\nu _{m})_{\lambda }\rangle =\delta ({\vec {k}}+{\vec {k'}})\beta \delta (\omega _{n}+\nu _{m})\left[{\begin{pmatrix}i\omega _{n}+\epsilon _{\vec {k}}-\mu &\Delta \\\Delta ^{*}&i\omega _{n}-\epsilon _{\vec {k}}+\mu \end{pmatrix}}^{-1}\right]_{\mu \lambda }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bcd57b5161b6317c7c6373367d5844345c511f7)























![{\displaystyle ={\frac {-1}{2\pi i}}2\pi i\left[{\frac {1}{(e^{\beta E_{\vec {k}}}+1)}}{\frac {1}{2E_{\vec {k}}}}+{\frac {1}{(e^{\beta E_{\vec {k}}}+1)}}{\frac {1}{-2E_{\vec {k}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56cb13c72d0527afb95afb70894c32e67b42d2df)
![{\displaystyle ={\frac {1}{2E_{\vec {k}}}}\left[{\frac {1}{(e^{-\beta E_{\vec {k}}}+1)}}-{\frac {1}{(e^{\beta E_{\vec {k}}}+1)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bb68f527e6c9c61f63ed31cd19d31e27ccb35cb)
![{\displaystyle ={\frac {1}{2E_{\vec {k}}}}\left[{\frac {1}{e^{-\beta E_{\vec {k}}/2}2\cosh(\beta E_{\vec {k}}/2)}}-{\frac {1}{e^{\beta E_{\vec {k}}/2}2\cosh(\beta E_{\vec {k}}/2)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa1f2a48f34e7adccafec30e9472ed87b61a3b09)
![{\displaystyle ={\frac {1}{4E_{\vec {k}}\cosh(\beta E_{\vec {k}}/2)}}\left[e^{\beta E_{\vec {k}}/2}2-e^{-\beta E_{\vec {k}}/2}2\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/328e35d100a50387129004e65ce5d85de8d91cc0)

































![{\displaystyle E_{\vec {k}}=\left[\epsilon ^{2}+\Delta ^{2}(T)\right]^{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61ee959a5fb5d9b86bdf322a0425d5fcd8e9a7dd)
![{\displaystyle \Rightarrow {\frac {1}{g}}=N_{\mu }\int _{0}^{\omega _{D}}d\epsilon {\frac {\tanh \left({\frac {\left[(\epsilon ^{2}+\Delta ^{2}(T)\right]^{\frac {1}{2}}}{2T}}\right)}{\left[\epsilon ^{2}+\Delta ^{2}(T)\right]^{\frac {1}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab6363e7fc0c9b5ecb88e9eaef707a249672f6e4)


![{\displaystyle T=0,{\frac {1}{g}}=N_{\mu }\int _{0}^{\omega _{D}}d\epsilon {\frac {1}{\left[\epsilon ^{2}+\Delta ^{2}\right]^{\frac {1}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25f0e7faaa71b1c914b7dbc1693648ff6164086e)















































![{\displaystyle Z=\int D\psi ^{*}D\psi \int D\Delta ^{*}D\Delta e^{-S_{BCS}-S_{\Delta }}=\int D\Delta ^{*}D\Delta e^{-S_{eff}[\Delta ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc75da74e3eeddecbc1153045fbb2150a8c425a9)
![{\displaystyle e^{-S_{eff}[\Delta _{0}\,]}\;=\;e^{-S_{\Delta }}\int D\psi ^{\ast }D\psi \;e^{-S_{BCS}[\Delta _{0\,}]}\;\sim e^{-\beta F}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb561c84a8ca54b3d3ace95384a4cb5672e82fdf)
![{\displaystyle e^{-\beta [F(\Delta _{0})-F(0)]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afe200c08157f11fc6dc825cbcbff7a56d186ca8)
![{\displaystyle ={\frac {e^{-S_{\Delta }}\int D\psi ^{\ast }D\psi e^{-S_{BCS}[\Delta _{0}\,]}}{\int D\psi ^{\ast }D\psi e^{-S_{BCS}[\,0\,]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc090099bafe6d9787539666065ef24e4f861ad0)


![{\displaystyle And\int D\psi ^{\ast }D\psi e^{-S_{BCS}[\Delta _{0}]}=\int D\psi ^{\ast }D\psi \,e^{-{\frac {1}{\beta }}}\sum _{\omega _{n}}\sum _{k}\psi _{k}^{\ast }(i\omega _{n}){\begin{pmatrix}i\omega _{n}+\epsilon _{k}-\mu &\Delta _{0}\\\Delta _{0}&i\omega _{n}-\epsilon _{k}+\mu \end{pmatrix}}\psi _{k}(i\omega _{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5683c7f55acf927c2c1a1a42101ce68c61a4406)

![{\displaystyle =const.\prod _{k}\prod _{n}{\frac {1}{\beta ^{2}}}[(i\omega _{n})^{2}-(\epsilon _{k}-\mu )^{2}-\Delta _{0}^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/600e7171d2ca147f29f716a8962af8f09a5f24ef)
![{\displaystyle \Rightarrow e^{-\beta [F(\Delta _{0})-F(0)]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/740f4a765854921e632ac4ba58e5d18902481744)
![{\displaystyle ={\frac {e^{-{\frac {\Delta _{0}^{2}}{\left|g\right|}}\beta N}const.{\prod _{k}^{}}{\prod _{n}^{}}{\frac {1}{\beta ^{2}}}[(i\omega _{n})^{2}-(\epsilon _{k}-\mu )^{2}-\Delta _{0}^{2}]}{const.{\prod _{k}^{}}{\prod _{n}^{}}{\frac {1}{\beta ^{2}}}[(i\omega _{n})^{2}-(\epsilon _{k}-\mu )^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dc2f7ed4b737bdca6e7c6dcae95c303adf9d4c8)


![{\displaystyle =e^{-\beta [F(\Delta _{0})-F(0)]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d214c7a2d488f25969fd2d2ef08ed85c7cb9c263)
![{\displaystyle {\frac {\delta S_{eff}[\Delta ]}{\delta \Re e\Delta (r,\tau )}}={\frac {2}{|g|}}\Re e\Delta (r,\tau )-{\frac {1}{\int D\psi ^{*}D\psi e^{-S_{0}-S_{int}}}}\int D\psi ^{*}D\psi e^{-S_{0}-S_{int}}\left(-{\frac {\delta S_{int}}{\delta \Re e\Delta (r,\tau )}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8d0430f47c546924c826c2dc158035a1939611d)


![{\displaystyle {\frac {\delta S_{eff}[\Delta ]}{\delta \Re e\Delta (r,\tau )}}={\frac {2}{|g|}}\Re e\Delta (r,\tau )+\langle \psi _{\downarrow }(r,\tau )\psi _{\uparrow }(r,\tau )+\psi _{\uparrow }^{*}(r,\tau )\psi _{\downarrow }^{*}(r,\tau )\rangle \ \ (1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c859207355c8b5068261342c2e600d55e120871)
![{\displaystyle {\frac {\delta S_{eff}[\Delta ]}{\delta \Im m\Delta (r,\tau )}}={\frac {2}{|g|}}\Im m\Delta (r,\tau )+i\langle \psi _{\uparrow }^{*}(r,\tau )\psi _{\downarrow }^{*}(r,\tau )-\psi _{\downarrow }(r,\tau )\psi _{\uparrow }(r,\tau )\rangle \ \ (2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a56a1ce35c5905b44cccb8e786430d58142ba32)
![{\displaystyle S_{eff}[\Delta (r,\tau )]=S_{eff}\left[\Delta _{sp}+(\Delta (r,\tau )-\Delta _{sp})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae0a7ffb130af4f2cef0403640d9fc80292406b7)


![{\displaystyle {\begin{aligned}&S_{eff}[\Delta _{sp}+(\Delta (r,\tau )-\Delta _{sp})]\\&=S_{eff}[\Delta _{sp}]+\int _{0}^{\beta }d\tau \int d^{3}r\Re e(\Delta (r,\tau )-\Delta _{sp}){\frac {\delta S_{eff}}{\delta \Re e\Delta (r,\tau )}}|_{\Delta _{sp}}+\int _{0}^{\beta }d\tau \int d^{3}r\Im m(\Delta (r,\tau )-\Delta _{sp}){\frac {\delta S_{eff}}{\delta \Im m\Delta (r,\tau )}}|_{\Delta _{sp}}\\&+{\frac {1}{2}}\int _{0}^{\beta }d\tau \int _{0}^{\beta }d\tau '\int d^{3}r\int d^{3}r'\Re e(\Delta (r,\tau )-\Delta _{sp})\Re e(\Delta (r',\tau ')-\Delta _{sp}){\frac {\delta ^{2}S_{eff}}{\delta \Re e\Delta (r,\tau )\delta \Re e\Delta (r',\tau ')}}|_{\Delta _{sp}}\\&+{\frac {1}{2}}\int _{0}^{\beta }d\tau \int _{0}^{\beta }d\tau '\int d^{3}r\int d^{3}r'\Im m(\Delta (r,\tau )-\Delta _{sp})\Im m(\Delta (r',\tau ')-\Delta _{sp}){\frac {\delta ^{2}S_{eff}}{\delta \Im m\Delta (r,\tau )\delta \Im m\Delta (r',\tau ')}}|_{\Delta _{sp}}\\&+\int _{0}^{\beta }d\tau \int _{0}^{\beta }d\tau '\int d^{3}r\int d^{3}r'\Re e(\Delta (r,\tau )-\Delta _{sp})\Im m(\Delta (r',\tau ')-\Delta _{sp}){\frac {\delta ^{2}S_{eff}}{\delta \Re e\Delta (r,\tau )\delta \Im m\Delta (r',\tau ')}}|_{\Delta _{sp}}+...\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59581ed21284b1c4699e88a1c81181343525c819)

![{\displaystyle {\begin{aligned}&{\frac {\delta ^{2}S_{eff}}{\delta \Re e\Delta (r,\tau )\delta \Re e\Delta (r',\tau ')}}\\&={\frac {2}{|g|}}\delta (\tau -\tau ')\delta (r-r')+{\frac {\delta }{\delta \Re e\Delta (r,\tau )}}\left[{\frac {1}{\int D\psi ^{*}D\psi e^{-S_{0}-S_{int}}}}\int D\psi ^{*}D\psi e^{-S_{0}-S_{int}}\left({\frac {\delta S_{int}}{\delta \Re e\Delta (r',\tau ')}}\right)\right]\\&={\frac {2}{|g|}}\delta (\tau -\tau ')\delta (r-r')-{\frac {\int D\psi ^{*}D\psi e^{-S_{0}-S_{int}}\left({\frac {\delta S_{int}}{\delta \Re e\Delta (r,\tau )}}\right)\left({\frac {\delta S_{int}}{\delta \Re e\Delta (r',\tau ')}}\right)}{\int D\psi ^{*}D\psi e^{-S_{0}-S_{int}}}}\\&+\left({\frac {\int D\psi ^{*}D\psi e^{-S_{0}-S_{int}}\left({\frac {\delta S_{int}}{\delta \Re e\Delta (r,\tau )}}\right)}{\int D\psi ^{*}D\psi e^{-S_{0}-S_{int}}}}\right)\left({\frac {\int D\psi ^{*}D\psi e^{-S_{0}-S_{int}}\left({\frac {\delta S_{int}}{\delta \Re e\Delta (r',\tau ')}}\right)}{\int D\psi ^{*}D\psi e^{-S_{0}-S_{int}}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b453ed8de40213b6b5184ac52d7077b1baa0d3b)








![{\displaystyle {\begin{aligned}{\frac {\delta ^{2}S_{eff}}{\delta \Re e\Delta (r,\tau )\delta \Re e\Delta (r',\tau ')}}|_{\Delta _{sp}}&={\frac {2}{|g|}}\delta (\tau -\tau ')\delta (r-r')-\langle \Psi ^{*}(r,\tau )\sigma _{x}\Psi (r,\tau )\Psi ^{*}(r',\tau ')\sigma _{x}\Psi (r',\tau ')\rangle ^{\mbox{con}}\\&={\frac {2}{|g|}}\delta (\tau -\tau ')\delta (r-r')+{\mbox{Tr}}\left[\sigma _{x}G(r-r',\tau -\tau ')\sigma _{x}G(r'-r,\tau '-\tau )\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5157218cc1d2545b33625d4287f0c68fe89d0324)






![{\displaystyle {\begin{aligned}\Pi _{--}(r-r',\tau -\tau ')&={\frac {2}{|g|}}\delta (\tau -\tau ')\delta (r-r')+{\mbox{Tr}}\left[\sigma _{y}G(r-r',\tau -\tau ')\sigma _{y}G(r'-r,\tau '-\tau )\right]\\\Pi _{-+}(r-r',\tau -\tau ')&=\langle \Psi ^{*}\sigma _{y}\Psi (r,\tau )\Psi ^{*}\sigma _{x}\Psi (r',\tau ')\rangle ^{\mbox{con}}=-{\mbox{Tr}}\left[\sigma _{y}G(r-r',\tau -\tau ')\sigma _{x}G(r'-r,\tau '-\tau )\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b731928f4c3e89fe9553b7e17596687904b4ae8)
![{\displaystyle {\begin{aligned}&S_{eff}[\Delta ]\approx S_{eff}[\Delta _{sp}]+\\&{\frac {1}{2}}{\frac {1}{\beta }}\sum _{\Omega _{n}}\sum _{q}\left[\delta \Delta _{+}(-q,-i\Omega _{n})\Pi _{++}(q,i\Omega _{n})\delta \Delta _{+}(q,i\Omega _{n})+\delta \Delta _{-}(-q,-i\Omega _{n})\Pi _{--}(q,i\Omega _{n})\delta \Delta _{-}(q,i\Omega _{n})\right.\\&\left.+2\delta \Delta _{-}(-q,-i\Omega _{n})\Pi _{-+}(q,i\Omega _{n})\delta \Delta _{+}(q,i\Omega _{n})\right]+...\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8a57110998c8550f5a1432f653a3259b4ae674e)


![{\displaystyle {\begin{aligned}\Pi _{++}(q,i\Omega _{n})&={\frac {2}{|g|}}+{\frac {1}{\beta }}\sum _{\omega _{n}}\int {\frac {d^{3}k}{(2\pi )^{3}}}{\mbox{Tr}}\left[\sigma _{1}G_{k+q}(i\omega _{n}+i\Omega _{n})\sigma _{1}G_{k}(i\omega _{n})\right]\\\Pi _{--}(q,i\Omega _{n})&={\frac {2}{|g|}}+{\frac {1}{\beta }}\sum _{\omega _{n}}\int {\frac {d^{3}k}{(2\pi )^{3}}}{\mbox{Tr}}\left[\sigma _{2}G_{k+q}(i\omega _{n}+i\Omega _{n})\sigma _{2}G_{k}(i\omega _{n})\right]\\\Pi _{-+}(q,i\Omega _{n})&=-{\frac {1}{\beta }}\sum _{\omega _{n}}\int {\frac {d^{3}k}{(2\pi )^{3}}}{\mbox{Tr}}\left[\sigma _{2}G_{k+q}(i\omega _{n}+i\Omega _{n})\sigma _{1}G_{k}(i\omega _{n})\right]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e009f14b7e5ce8e6e06ccc4d136f7969513945d0)
![{\displaystyle {\begin{aligned}&{\mbox{Tr}}\left[\sigma _{1,2}{\frac {(i\omega _{n}+i\Omega _{n})\mathbb {I} +(\epsilon _{k+q}-\mu )\sigma _{3}+\Delta _{sp}\sigma _{1}}{(\omega _{n}+\Omega _{n})^{2}+(\epsilon _{k+q}-\mu )^{2}+\Delta _{sp}^{2}}}\sigma _{1,2}{\frac {i\omega _{n}\mathbb {I} +(\epsilon _{k}-\mu )\sigma _{3}+\Delta _{sp}\sigma _{1}}{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}+\Delta _{sp}^{2}}}\right]\\=&2{\frac {(i\omega _{n}+i\Omega _{n})i\omega _{n}-(\epsilon _{k+q}-\mu )(\epsilon _{k}-\mu )\pm \Delta _{sp}^{2}}{\left[(\omega _{n}+\Omega _{n})^{2}+(\epsilon _{k+q}-\mu )^{2}+\Delta _{sp}^{2}\right]\left[\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}+\Delta _{sp}^{2}\right]}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c98640794b399e15a7be828c387033d8e8fd2a5a)
![{\displaystyle {\begin{aligned}&{\mbox{Tr}}\left[\sigma _{2}{\frac {(i\omega _{n}+i\Omega _{n})\mathbb {I} +(\epsilon _{k+q}-\mu )\sigma _{3}+\Delta _{sp}\sigma _{1}}{(\omega _{n}+\Omega _{n})^{2}+(\epsilon _{k+q}-\mu )^{2}+\Delta _{sp}^{2}}}\sigma _{1}{\frac {i\omega _{n}\mathbb {I} +(\epsilon _{k}-\mu )\sigma _{3}+\Delta _{sp}\sigma _{1}}{\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}+\Delta _{sp}^{2}}}\right]\\=&{\frac {(i\omega _{n}+i\Omega _{n})(\epsilon _{k}-\mu ){\mbox{Tr}}[\sigma _{2}\sigma _{1}\sigma _{3}]+i\omega _{n}(\epsilon _{k+q}-\mu ){\mbox{Tr}}[\sigma _{2}\sigma _{3}\sigma _{1}]}{\left[(\omega _{n}+\Omega _{n})^{2}+(\epsilon _{k+q}-\mu )^{2}+\Delta _{sp}^{2}\right]\left[\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}+\Delta _{sp}^{2}\right]}}\\=&{\frac {(i\omega _{n}+i\Omega _{n})(\epsilon _{k}-\mu )(-2i)+i\omega _{n}(\epsilon _{k+q}-\mu )2i}{\left[(\omega _{n}+\Omega _{n})^{2}+(\epsilon _{k+q}-\mu )^{2}+\Delta _{sp}^{2}\right]\left[\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}+\Delta _{sp}^{2}\right]}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/822f1eb33367802b8bcc911b3e1f20503f2031c2)



![{\displaystyle {\begin{aligned}\Pi _{--}(0,0)&={\frac {2}{|g|}}-{\frac {1}{\beta }}\sum _{\omega _{n}}\int {\frac {d^{3}k}{(2\pi )^{3}}}2{\frac {1}{[\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}+\Delta _{sp}^{2}]}}\\&={\frac {2}{|g|}}+2\int {\frac {d^{3}k}{(2\pi )^{3}}}{\frac {1}{\beta }}\sum _{\omega _{n}}{\frac {1}{(i\omega _{n}-E_{k})(i\omega _{n}+E_{k})}}\\&={\frac {2}{|g|}}+2\int {\frac {d^{3}k}{(2\pi )^{3}}}\left({\frac {n_{F}(E_{k})}{2E_{k}}}-{\frac {n_{F}(-E_{k})}{2E_{k}}}\right)\\&=2\left({\frac {1}{|g|}}-\int {\frac {d^{3}k}{(2\pi )^{3}}}{\frac {1-2n_{F}(E_{k})}{2E_{k}}}\right)\\&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c40535d9ca107e71544cac6a44d023322a6348fb)
![{\displaystyle {\begin{aligned}\Pi _{++}(0,0)&={\frac {2}{|g|}}+{\frac {1}{\beta }}\sum _{\omega _{n}}\int {\frac {d^{3}k}{(2\pi )^{3}}}2{\frac {-\omega _{n}^{2}-(\epsilon _{k}-\mu )^{2}+\Delta _{sp}^{2}}{[\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}+\Delta _{sp}^{2}]^{2}}}\\&=4\Delta _{sp}^{2}{\frac {1}{\beta }}\sum _{\omega _{n}}\int {\frac {d^{3}k}{(2\pi )^{3}}}{\frac {1}{[\omega _{n}^{2}+(\epsilon _{k}-\mu )^{2}+\Delta _{sp}^{2}]^{2}}}\\&=4\Delta _{sp}^{2}N_{0}{\frac {1}{\beta }}\sum _{\omega _{n}}\int _{-\infty }^{\infty }{\frac {d\xi }{[\xi ^{2}+\omega _{n}^{2}+\Delta _{sp}^{2}]^{2}}}\\&=4\Delta _{sp}^{2}N_{0}{\frac {1}{\beta }}\sum _{\omega _{n}}{\frac {\pi }{2}}{\frac {1}{(\omega _{n}^{2}+\Delta _{sp}^{2})^{\frac {3}{2}}}}\\&=2\pi N_{0}\Delta _{sp}^{2}{\frac {1}{\pi ^{3}T^{2}}}\sum _{n=-\infty }^{\infty }{\frac {1}{[(2n+1)^{2}+({\frac {\Delta _{sp}}{\pi T}})^{2}]^{\frac {3}{2}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2548cd81de309a79ee7a0fe811931f76c45148e1)

![{\displaystyle {\begin{aligned}\sum _{n=-\infty }^{\infty }{\frac {1}{[(2n+1)^{2}+({\frac {\Delta _{sp}}{\pi T}})^{2}]^{\frac {3}{2}}}}&={\frac {2}{\sqrt {\pi }}}\int _{0}^{\infty }d\lambda {\sqrt {\lambda }}e^{-\lambda ({\frac {\Delta _{sp}}{\pi T}})^{2}}\left(\sum _{n=-\infty }^{\infty }e^{-\lambda (2n+1)^{2}}\right)\\&={\frac {2}{\sqrt {\pi }}}\int _{0}^{\infty }d\lambda {\sqrt {\lambda }}e^{-\lambda ({\frac {\Delta _{sp}}{\pi T}})^{2}}\Theta _{2}(0,e^{-4\lambda })\\&={\frac {1}{4{\sqrt {\pi }}}}\int _{0}^{\infty }d\xi {\sqrt {\xi }}e^{-\xi ({\frac {\Delta _{sp}}{2\pi T}})^{2}}\Theta _{2}(0,e^{-\xi })\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eefd3537b371f2ba2137d3f3d13c0cb5578cf10a)

![{\displaystyle {\begin{aligned}\Pi _{++}(0,0)&=2\pi N_{0}\Delta _{sp}^{2}{\frac {1}{\pi ^{3}T^{2}}}\sum _{n=-\infty }^{\infty }{\frac {1}{[(2n+1)^{2}+({\frac {\Delta _{sp}}{\pi T}})^{2}]^{\frac {3}{2}}}}\\&=2N_{0}\Phi ({\frac {\Delta _{sp}}{2\pi T}})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/549e8ab5876c7601c68da54f9ddfb08b2d2bb3e1)

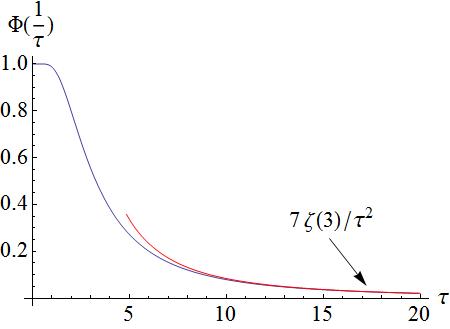















![{\displaystyle ={\frac {2}{\beta }}\sum _{\omega _{n}}{\int {{\frac {d^{3}k}{(2\pi )^{3}}}\left[{\frac {1}{\omega _{n}^{2}+E_{k}^{2}}}-{\frac {\omega _{n}\left(\omega _{n}+\Omega _{n}\right)+\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\mu \right)-\Delta _{sp}^{2}}{\left(\omega _{n}^{2}+E_{k}^{2}\right)\left(\left(\omega _{n}+\Omega _{n}\right)^{2}+E_{k+q}^{2}\right)}}-{\frac {2\Delta _{sp}^{2}}{\left(\omega _{n}^{2}+E_{k}^{2}\right)^{2}}}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9b31459f537fc25bc99f02d5da6d74f23ea09fd)
![{\displaystyle ={\frac {2}{\beta }}\sum _{\omega _{n}}{\int {{\frac {d^{3}k}{(2\pi )^{3}}}\left[{\frac {\omega _{n}^{2}+\left(\epsilon _{k}-\mu \right)^{2}-\Delta _{sp}^{2}}{\left(\omega _{n}^{2}+E_{k}^{2}\right)^{2}}}-{\frac {\omega _{n}\left(\omega _{n}+\Omega _{n}\right)+\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\mu \right)-\Delta _{sp}^{2}}{\left(\omega _{n}^{2}+E_{k}^{2}\right)\left(\left(\omega _{n}+\Omega _{n}\right)^{2}+E_{k+q}^{2}\right)}}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/945ffe0040fc678eeda4cde7d4b9bd32099178c2)
![{\displaystyle ={\frac {2}{\beta }}\sum _{\omega _{n}}{\int {{\frac {d^{3}k}{(2\pi )^{3}}}\left[{\frac {\omega _{n}^{2}+E_{k}^{2}-2\Delta _{sp}^{2}}{\left(\omega _{n}^{2}+E_{k}^{2}\right)^{2}}}-{\frac {\omega _{n}^{2}+E_{k}^{2}+\omega _{n}\Omega _{n}+\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\epsilon _{k}\right)-2\Delta _{sp}^{2}}{\left(\omega _{n}^{2}+E_{k}^{2}\right)\left(\omega _{n}^{2}+E_{k}^{2}+2\omega _{n}\Omega _{n}+\Omega _{n}^{2}+\left(\epsilon _{k+q}-\mu \right)^{2}-\left(\epsilon _{k}-\mu \right)\right)}}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46e815c0db1ece7de73c89c7b32eb48fe20ccaaa)

![{\displaystyle ={\frac {\omega _{n}^{2}+E_{k}^{2}-2\Delta _{sp}^{2}+\omega _{n}\Omega _{n}+\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\epsilon _{k}\right)}{\left(\omega _{n}^{2}+E_{k}^{2}\right)^{2}}}\left[1+{\frac {2\omega _{n}\Omega _{n}+\Omega _{n}^{2}+\left(\epsilon _{k+q}-\epsilon _{k}\right)\left(\epsilon _{k+q}+\epsilon _{k}-2\mu \right)}{\omega _{n}^{2}+E_{k}^{2}}}\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a853af12a0826e4adf5e6f444bf8e89d9534423b)















![{\displaystyle {\begin{aligned}\Pi _{--}\left(q,i\Omega _{n}\right)&={\frac {2}{\beta }}\sum _{\omega _{n}}{\int {{\frac {d^{3}k}{(2\pi )^{3}}}\left[{\frac {1}{\omega _{n}^{2}+E_{k}^{2}}}-{\frac {\omega _{n}\left(\omega _{n}+\Omega _{n}\right)+\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\mu \right)+\Delta _{sp}^{2}}{\left(\omega _{n}^{2}+E_{k}^{2}\right)\left(\left(\omega _{n}+\Omega _{n}\right)^{2}+E_{k+q}^{2}\right)}}\right]}}\\&={\frac {2}{\beta }}\sum _{\omega _{n}}{\int {{\frac {d^{3}k}{(2\pi )^{3}}}\left[{\frac {1}{\omega _{n}^{2}+E_{k}^{2}}}-{\frac {\omega _{n}^{2}+\left(\epsilon _{k}-\mu \right)^{2}+\Delta _{sp}^{2}+\omega _{n}\Omega _{n}+\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\epsilon _{k}\right)}{\left(\omega _{n}^{2}+E_{k}^{2}\right)\left(\omega _{n}^{2}+2\omega _{n}\Omega _{n}+\Omega _{n}^{2}+E_{k}^{2}+\left(\epsilon _{k+q}-\mu \right)^{2}-\left(\epsilon _{k}-\mu \right)^{2}\right)}}\right]}}\\&={\frac {2}{\beta }}\sum _{\omega _{n}}{\int {{\frac {d^{3}k}{(2\pi )^{3}}}\left[{\frac {1}{\omega _{n}^{2}+E_{k}^{2}}}-{\frac {\omega _{n}^{2}+E_{k}^{2}+\omega _{n}\Omega _{n}+\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\epsilon _{k}\right)}{\left(\omega _{n}^{2}+E_{k}^{2}\right)^{2}\left(1+{\frac {\Omega _{n}^{2}+2\omega _{n}\Omega _{n}+\left(\epsilon _{k+q}-\epsilon _{k}\right)\left(\epsilon _{k+q}+\epsilon _{k}-2\mu \right)}{\omega _{n}^{2}+E_{k}^{2}}}\right)}}\right]}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fffee7e1c7dadc4a3d43d5f5547f4905cc7d8faa)
![{\displaystyle \left[{\frac {1}{\omega _{n}^{2}+E_{k}^{2}}}+{\frac {\omega _{n}\Omega _{n}+\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\epsilon _{k}\right)}{\left(\omega _{n}^{2}+E_{k}^{2}\right)^{2}}}\right]\left(1+{\frac {\Omega _{n}^{2}+2\omega _{n}\Omega _{n}+\left(\epsilon _{k+q}-\epsilon _{k}\right)\left(\epsilon _{k+q}+\epsilon _{k}-2\mu \right)}{\omega _{n}^{2}+E_{k}^{2}}}\right)^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32cc24fef053ceb23f77238f69ee282c6ff6ae9e)

![{\displaystyle \Pi _{--}\left(q,i\Omega _{n}\right)\simeq {\frac {2}{\beta }}\sum _{\omega _{n}}{\int {{\frac {d^{3}k}{(2\pi )^{3}}}\left[{\frac {\Omega _{n}^{2}+\left(\epsilon _{k+q}-\epsilon _{k}\right)^{2}}{\left(\omega _{n}^{2}+E_{k}^{2}\right)^{2}}}-{\frac {2\omega _{n}^{2}\Omega _{n}^{2}+2\left(\epsilon _{k}-\mu \right)^{2}\left(\epsilon _{k+q}-\epsilon _{k}\right)^{2}}{\left(\omega _{n}^{2}+E_{k}^{2}\right)^{3}}}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e99911c69bbdacfe8caa2a502155ca9299cddaf3)
![{\displaystyle \Pi _{--}\left(q,i\Omega _{n}\right)\simeq 2N_{0}\int _{-\infty }^{\infty }{{\frac {d\omega }{2\pi }}\int _{-\infty }^{\infty }{d\xi \left[{\frac {\Omega _{n}^{2}+{\frac {1}{3}}v_{F}^{2}q^{2}}{\left(\omega ^{2}+\xi ^{2}+\Delta _{sp}^{2}\right)^{2}}}-2{\frac {\omega ^{2}\Omega _{n}^{2}+\xi ^{2}{\frac {1}{3}}v_{F}^{2}q^{2}}{\left(\omega ^{2}+\xi ^{2}+\Delta _{sp}^{2}\right)^{3}}}+\ldots \right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7ec81aee0214db3b74621826be49c3ecac7e2d4)

![{\displaystyle {\begin{aligned}\Pi _{-+}\left(q,i\Omega _{n}\right)=&-{\frac {1}{\beta }}\sum _{\omega _{n}}{\int {{\frac {d^{3}k}{(2\pi )^{3}}}{\frac {\left(i\omega _{n}+i\Omega _{n}\right)\left(\epsilon _{k}-\mu \right)\left(-2i\right)+i\omega _{n}\left(\epsilon _{k+q}-\mu \right)\cdot 2i}{\left[\left(\omega _{n}+\Omega _{n}\right)^{2}+\left(\epsilon _{k+q}-\mu \right)^{2}+\Delta _{sp}^{2}\right]\left[\omega _{n}^{2}+\left(\epsilon _{k}-\mu \right)^{2}+\Delta _{sp}^{2}\right]}}}}\\&=-{\frac {1}{\beta }}\sum _{\omega _{n}}{\int {{\frac {d^{3}k}{(2\pi )^{3}}}{\frac {2\Omega _{n}\left(\epsilon _{k}-\mu \right)-2\omega _{n}\left(\epsilon _{k+q}-\epsilon _{k}\right)}{\omega _{n}^{2}+2\omega _{n}\Omega _{n}+\Omega _{n}^{2}+E_{k}^{2}+\left(\epsilon _{k+q}-\epsilon _{k}\right)\left(\epsilon _{k+q}+\epsilon _{k}-2\mu \right)}}\cdot {\frac {1}{\omega _{n}^{2}+E_{k}^{2}}}}}\\&=-{\frac {1}{\beta }}\sum _{\omega _{n}}{\int {{\frac {d^{3}k}{(2\pi )^{3}}}{\frac {2\Omega _{n}\left(\epsilon _{k}-\mu \right)-2\omega _{n}\left(\epsilon _{k+q}-\epsilon _{k}\right)}{\left(\omega _{n}^{2}+E_{k}^{2}\right)^{2}\left(1+{\frac {2\omega _{n}\Omega _{n}+\Omega _{n}^{2}+\left(\epsilon _{k+q}-\epsilon _{k}\right)\left(2\left(\epsilon _{k}-\mu \right)+\epsilon _{k+q}-\epsilon _{k}\right)}{\omega _{n}^{2}+E_{k}^{2}}}\right)}}}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc678fbb28408f4cbd07d46ef38cfb93a8520b56)
![{\displaystyle \left[1+{\frac {2\omega _{n}\Omega _{n}+2\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\epsilon _{k}\right)+\left(\epsilon _{k+q}-\epsilon _{k}\right)^{2}+\Omega _{n}^{2}}{\omega _{n}^{2}+E_{k}^{2}}}\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70006e673059d88dabea95c2784225866b6a15f5)
![{\displaystyle {\begin{aligned}=1&-{\frac {2\omega _{n}\Omega _{n}+2\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\epsilon _{k}\right)+\left(\epsilon _{k+q}-\epsilon _{k}\right)^{2}+\Omega _{n}^{2}}{\omega _{n}^{2}+E_{k}^{2}}}\\&+{\frac {\left[2\omega _{n}\Omega _{n}+2\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\epsilon _{k}\right)+\left(\epsilon _{k+q}-\epsilon _{k}\right)^{2}+\Omega _{n}^{2}\right]^{2}}{\left(\omega _{n}^{2}+E_{k}^{2}\right)^{2}}}\\&-{\frac {\left[2\omega _{n}\Omega _{n}+2\left(\epsilon _{k}-\mu \right)\left(\epsilon _{k+q}-\epsilon _{k}\right)+\left(\epsilon _{k+q}-\epsilon _{k}\right)^{2}+\Omega _{n}^{2}\right]^{3}}{\left(\omega _{n}^{2}+E_{k}^{2}\right)^{3}}}+\ldots \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4889fcc3b033fdc73d2f347d046f4e3d7f0aa86)






![{\displaystyle \left[{\begin{array}{cc}\delta \Delta _{+}\left(-q,-i\Omega _{n}\right)&\delta \Delta _{-}\left(-q,-i\Omega _{n}\right)\end{array}}\right]\left[{\begin{array}{cc}m^{2}+{\frac {1}{3}}\rho \left(\Omega _{n}^{2}+c^{2}q^{2}\right)&\alpha \Omega _{n}\\\alpha \Omega _{n}&\rho \left(\Omega _{n}^{2}+c^{2}q^{2}\right)\end{array}}\right]\left[{\begin{array}{cc}\delta \Delta _{+}\left(q,i\Omega _{n}\right)\\\delta \Delta _{-}\left(q,i\Omega _{n}\right)\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/146c95bc61b75cc527d0aa008844ed1fcaae9a36)
![{\displaystyle {\begin{aligned}&{\frac {1}{2}}m^{2}+{\frac {2}{3}}\rho \left(\Omega _{n}^{2}+c^{2}q^{2}\right)&\pm {\sqrt {\left[{\frac {1}{2}}m^{2}-{\frac {1}{3}}\rho \left(\Omega _{n}^{2}+c^{2}q^{2}\right)\right]^{2}+\alpha ^{2}\Omega _{n}^{2}}}\\\simeq &{\frac {1}{2}}m^{2}+{\frac {2}{3}}\rho \left(\Omega _{n}^{2}+c^{2}q^{2}\right)&\underbrace {\pm \left({\frac {1}{4}}m^{4}-{\frac {m^{2}}{3}}\rho \left(\eta \Omega _{n}^{2}+c^{2}q^{2}\right)+\ldots \right)^{\frac {1}{2}}} _{\begin{array}{clr}\Downarrow \\\pm {\frac {1}{2}}m^{2}\left(1-{\frac {1}{3}}{\frac {\rho }{m^{2}}}\left(\eta \Omega _{n}^{2}+c^{2}q^{2}\right)+\ldots \right)\end{array}}\\\simeq &\left\{{\begin{array}{rcl}m^{2}+{\frac {1}{3}}\left(\eta '\Omega _{n}^{2}+c^{2}q^{2}\right)\\\rho \left(\eta '\Omega _{n}^{2}+c^{2}q^{2}\right)\end{array}}\right.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/786fe5e8a8be72aa9cc67f43c37f51530dbcb52d)

