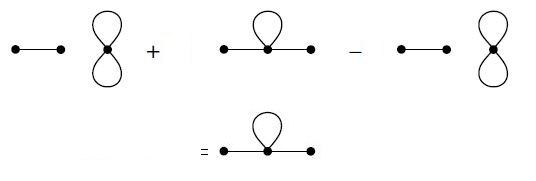
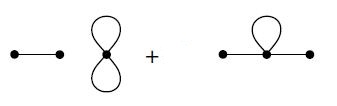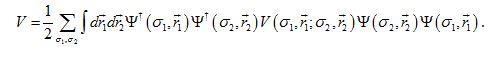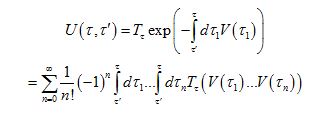Phy5670
Welcome to the Quantum Many Body Physics PHY5670 Fall2010/2011/2012
PHY5670 is a one semester graduate level course. Its aim is to introduce basic concepts, and logical framework, of this vast and developing discipline: broken symmetry and adiabatic continuity. Theoretical techniques, such as coherent state path integrals and diagrammatic perturbation expansions, will be used to emphasize these deeper underlying concepts, as well as to provide practical means of calculations. Few illustrative physical systems and quantum many-body models will also be studied.
The key component of the course is the collaborative student contribution to the course Wiki-textbook. Each team of students is responsible for BOTH writing the assigned chapter AND editing chapters of others.
Team assignments:
Outline of the course:
Conceptual basis of many body physics
Broken symmetry
As symmetries can heavily constrain the variables describing a system and often dictate the ansatz for a solution, their analysis is generally the first step taken dealing with a certain problem. The concept of broken symmetry, where the symmetry is less obvious (but nevertheless present) is a very powerful tool in Quantum Many Body physics as well as in many other fields. One example is High energy physics, where broken symmetries play a dominant role and one central effort is the search for the mechanism of electroweak symmetry breaking, whether it is the proposed Higgs particle or a more complex solution. In 2008, the Nobel prize in physics was awarded to one half to Yoichiro Nambu "for the discovery of the mechanism of spontaneous broken symmetry in subatomic physics". The other half went jointly to Makoto Kobayashi and Toshihide Maskawa "for the discovery of the origin of the broken symmetry which predicts the existence of at least three families of quarks in nature".
In the following, we will explain the concept of broken symmetries and highlight applications in many body physics.
What is broken symmetry?
Our experience shows us, then, that as matter cools down it usually no longer retains the full symmetry of the basic laws of quantum mechanics which it undoubtedly obeys; our task here is to understand that the questions we must ask are "Why", "In what sense", and "What are the consequences?" P.W. Anderson (Basic Notions of Condensed Matter Physics)

A system of particles is defined by its Hamiltonian which describes the different interactions between the particles. Different systems can present many types of symmetries, e.g. translational or rotational symmetry. Whenever a system is found in a state that is less symmetric than the Hamiltonian describing that system, we say this symmetry is broken. Knowledge about the underlying symmetries of a system is essential for a mathematical description.
There is an essential difference between the statements a symmetry is broken and a symmetry is absent. Even a symmetry that is broken is of crucial importance to the phenomenology of the system, since the underlying Hamiltonian still exhibits the symmetry. For example, a system of Ising spins at zero external field undergoes a second order phase transition to a ferromagnet state when it is cooled below the Curie-Temperature. In contrast, if an external field, explicitly breaking the symmetry between spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \uparrow} and spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downarrow } configurations, is applied to the system the transition is first order.
Typical symmetries that are important for many-body systems are translational symmetry, rotational symmetry, time-reversal symmetry and gauge symmetries. When a system crystallizes, translational symmetries are broken. (The probability to find a particle at a specific location is not longer constant, instead it is a function displaying peaks at the locations corresponding to the lattice points). Rotational symmetry or isotropy is broken for example in liquid crystals, where the constituting molecules are non-spherical and align with each other, thus choosing a preferred direction for the macroscopic system. Gauge symmetries are broken in superconductors or superfluids, where bosons condensate into a single phase, and time-reversal symmetries are spontaneously broken for example by ferromagnets with aligned spins.
A transition between states of different symmetry is automatically a phase transition (but not each phase transition is accompanied by symmetry breaking). Many phase transitions that exhibit symmetry breaking are of second order or continuous phase transitions. Examples are ferromagnets, antiferromagnets or superconductors. Second order phase transitions do not - in contrast to first order phase transitions - involve latent heat. An example of a first order phase transition with symmetry breaking is the liquid-to-solid-transition. The transition from liquid to gas is also of first order, but involves no symmetry change.
The distinction between phase transitions with and without symmetry breaking is very important, since the phenomena that can occur in each state are dictated by the symmetry exhibited. For example, it is only possible to get from one phase into another without crossing a phase border if both phases exhibit the same symmetry (as liquid and gaseous water), while phases with different symmetries are necessarily disjoint. These issues will be discussed in more detail in chapter 1.1.2.
Obviously, systems in different symmetry states cannot be solved with the same approach. Therefore it is crucial to define the symmetries of a given system before engaging in calculations.
"Why" broken symmetry?
Under surprisingly general circumstances the lowest energy state of a system does not have the total symmetry group of its Hamiltonian, and so in the absence of thermal fluctuations the system assumes an unsymmetrical state. P.W. Anderson (Basic Notions of Condensed Matter Physics)
While each system exhibits different symmetries and different symmetry breaking patterns, a general rule of thumb is that broken symmetries are to be expected whenever the potential energy in a system dominates the kinetic energy. Reversely, symmetries can be restored by going to higher temperatures (raising the kinetic energy).
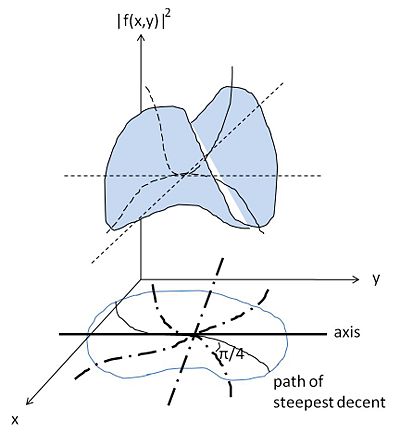
The essential phenomenon in either case is that the lowest state of a potential energy of interaction between the particles -- for example, a pair interaction
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle V_{tot}=\sum_{i<j}V(| r_i-r_j|)}
-- must occur for either a unique relative configuration of all particles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{r_1,r_2,\ldots r_N\}} and all translations and rotations, or, in artificial cases, perhaps for a highly restricted subset of all configurations. P.W. Anderson (Basic Notions of Condensed Matter Physics)
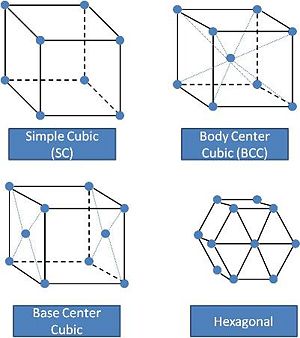
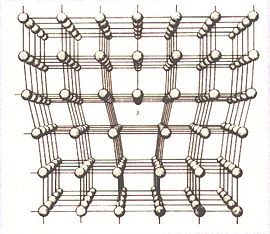
When all particles have a "unique relative configuration", the system has crystallized. There is a finite number of possible lattice structures (some examples of 3 dimensional lattices are shown above). It is easy to see that these lattices only obey discrete symmetries (translation by a integer multiple of the lattice spacing, or rotations by certain fixed angles) instead of the contious rotational and translational symmetries of a gas or liquid.
It is then clear that in any situation where the potential energy dominates kinetic energy and entropy, as in the two cases mentioned, a system of particles obeying a simple potential will take up a regular lattice structure. P.W. Anderson (Basic Notions of Condensed Matter Physics)
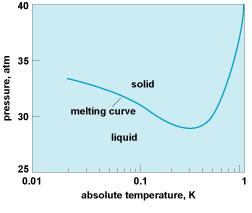
The less symmetric state tends to be one lower in temperature, simply because the more symmetric one is usually a distribution of thermal fluctuations among all the available values of the order parameter . But this order of phases is not a general rule; 3He, for instance, violates it because the solid has a greater nuclear paramagnetic entropy than liquid, and at low temperatures the melting curve has a negative slope. So in this temperature regime, the solid is the high-temperature phase and the liquid is the low-temperature phase. P.W. Anderson ("Basic Notions of Condensed Matter Physics")
The example of 3He, and the underlying reason for its atypical behavior will be discussed below.
Symmetry breaking and the thermodynamic limit
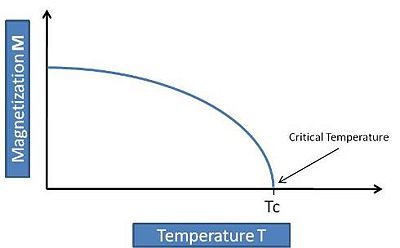
The transition between states of different symmetry can be characterized in terms of an order parameter, which is defined (in the sense of Landau) as any parameter that is zero in the symmetric phase (disordered phase) and non-zero in the broken symmetry phase (ordered phase). An example is the magnetization in a ferromagnet that is zero above a critical temperature Tc and finite, different than zero, for T<Tc (see figure). Note that there can be various different choices for the order parameter of a system. In a crystal, the density Fourier components corresponding to reciprocal lattice vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \rho_{\vec{G}} } is an order parameter as well as the shear strength Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \tau } .
In particular, the free energy F of the system is non-analytic at the transition between phases of different symmetries. This is due to the fact that F depends non-trivially on the order parameter in the non-symmetric phase, while in the symmetric phase F cannot depend on the order parameter (which is forced to zero by virtue of the symmetry).
The non-analyticity of the free energy at the phase transition is only possible in the thermodynamic limit, i.e. for systems with infinite number of particles. The reason behind this is that any finite sum over the analytic functions describing the individual contributions to the free energy of each particle will again be analytic. However, an infinite sum of analytic functions can be non-analytic. (For example, the non-analytic step function can be written as an infinite Fourier sum over analytic trigonometric functions.)
Another way to see the necessity of the thermodynamic limit is by use of the principle of ergodicity. By this principle, any two states of a system that are degenerate in symmetry should be equally probable and therefore equally populated. This means if there are several ground states, the system will constantly fluctuate between them. An example is a set of N=2 spins that are energetically preferred to be aligned. Suppose a system initially is in an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state. Now at finite temperature there will be a certain rate of fluctuations flipping an arbitrary spin so the state of the system is changed to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \uparrow \downarrow } or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downarrow \uparrow} . In order to minimize energy, the spins will realign. However, the return to the initial Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state is just as likely as the transition to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downdownarrows } . Over time, the system will be found in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \upuparrows } state just as often as in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downdownarrows } state, and the overall magnetization will be zero. This will still be true for N=2,3,... and in fact any finite N. However, the higher the number of sites, the more spins have to be flipped in order for the system to go from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \uparrow \uparrow \uparrow \ldots } to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \downarrow \downarrow \downarrow \ldots } , and the typical time span the system needs to change from one ground state into another grows. For a system with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=\infty } , ergodicity is broken, because even if each ground state is in principle equally likely, the system will stay in its initial state forever.
Of course, no real ferromagnet, crystal or other experimental system is truly infinite. However, typical macroscopic system sizes of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle N=10^{23}} are enough to make the lifetime of any initial ground state longer than the age of the universe. The system is frozen into one particular ground state; the symmetry connecting different ground states is dynamically broken.
By reversion of this argument, it is easy to see that spontaneous symmetry breaking is impossible in any microscopic system, such as molecules.
Examples
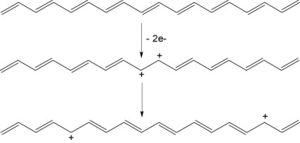
Wigner Crystals
A uniform gas of electrons on a neutralizing background (jellium model) will crystallize if the electron density falls below a critical value. The reason is that at low densities the potential energy due to Coulomb interactions between electrons dominates over their kinetic energy. The existence of a crystalline phase was first predicted by Eugene Wigner in 1934. At zero temperature, the dimensionless Wigner-Seitz radius Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle r_s=a/a_B } characterizes the state of a uniform electron gas, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle a } is the average inter-particle spacing and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle a_B } is the Bohr radius. The critical value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle r_s} , above which the system form a Wigner crystal, can be determined by quantum Monte Carlo simulations. The Wigner crystal is peculiar in the sense that in contrast to most other crystal it melts when the density is increased.
Wigner crystals of heavy ions have been postulated to exist inside of white dwarfs.
Helium-3
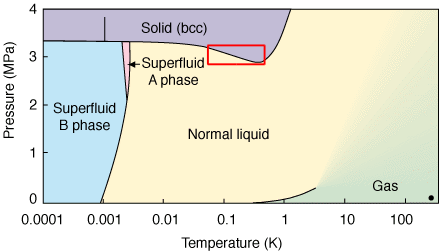
The Helium-3 isotope has two protons and one neutron. This makes He-3 a fermionic system subject to the Fermi exclusion principle. At very low temperatures, He-3 will crystallize, and therewith spontaneously break translational symmetry.
The phase diagram of He-3 displays a curiosity: there is a region where decreasing the temperature leads to a transitions from solid to liquid state (see the red square in the phase diagram above). Usually it is the other way around, the temperature has to be increased to go from solid to liquid phase (melting). While the opposite behavior in the case of He-3 looks paradoxical at first, it is in fact perfectly logical: Within the red square, the system has more entropy than the solid state than in the liquid state because of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^N } possible spin orientations in the crystal.
At very low temperatures and pressures it could be possible to observe a superfluid phase in the He-3. To explain this phase we can again use the concept of broken symmetry. The symmetries of He-3 are that of the spin and orbital rotations (9 degrees of freedom); and gauge invariance.
The superfluid He-3 presents intself in two different phases, discovered in 1970's. These phases are called A-phase and B-phase. In the B-phase the angular momentum and spin are isotropic and the total angular momentum is J=S+L=0. In the A-phase the spin and angular momentum are anisotropic. Therefore to pass from the B-phase to the A-phase angular momentum isotropy has to be broken.
Many properties of He-3 have been predicted using the theory of broken symmetry, even though the order parameter is very complicated because the many degrees of freedom. We can see that the theoretical concepts of quantum many body physics, in particular the concept of broken symmetry, have direct application to understand the behavior of real systems as the He-3.
Other examples
In the next chart we show and compare different systems that exhibit broken symmetry.
| Example | Disordered Phase | Ordered Phase | Order Parameter | Is the order parameter a constant of motion? |
| Ferromagnetism | Paramagnet | Ferromagnet | Magnetization M | Yes |
| Antiferromagnetism | Paramagnet | Antiferromagnet | Sublattice magnetization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{sl}} | No |
| Superconductivity | Normal Metal | Superconductor | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \Psi_{\sigma}^*, \Psi_{-\sigma}^*\rangle } | No |
| Crystal | Liquid | Solid | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\vec{G}}} , shear strength Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} | No |
| He 3 | Normal liquid | Anisotropic superfluid | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{ij}=<\Psi\Psi>_{M_L,M_S}} | No |
Note: To see more details and other phenomena you can check "P.W. Anderson(Basic Notions of Condensed Matter Physics), pg.68"
As we can imagine there are just few examples were the order parameter is a constant of motion. The Ferromagnetism is one them, where we can take the order parameter as the total spin in some direction, but this is not a common case.
Consequences of broken symmetry
- Discreteness of phase transitions, and the resulting failure of continuation: disjointness of physical phases
- Development of collective excitations
- Generalized rigidity
- Defect structures: dissipation and topological considerations
Discreteness and Disjointness
First theorem "It is impossible to change symmetry gradually. A given symmetry element is either there or it is not; there is no way for it to grow imperceptibly" (Landau and Lifshitz, 1958)
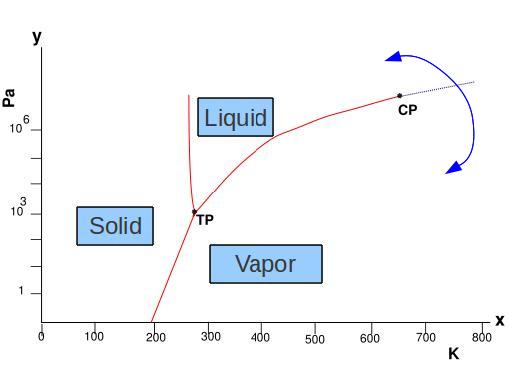
Let's analyze the phase diagram of the water (see figure above). As we can see in the diagram we can go from vapor to liquid in a "smooth path" just going around the critical point, actually this means that these two phases doesn't present a broken symmetry. On the other hand, it's impossible to go from liquid to solid smoothly (or in opposite way). The liquid-gas transition is typical of a symmetry-nonbreaking transition. There is no possibility that the fluid and gas can be in equilibrium at the same density except at a point on the boiling curve.
In the cases of true broken symmetry, the unsymmetrical state is normally characterized by an "order parameter". By Landau's definition this is simply any parameter that is zero in the symmetric state and has a nonzero average when the symmetry is broken. It is an additional variable necessary to specify the microscopic state in the lower symmetry state. Thus by breaking symmetry a new variable is created. For example, in a nonmagnetic material the order parameter is the magnetization M, which in the absence of a magnetic field is zero by time-reversal symmetry. The state in that case is specified by the usual intensive variables P and T.
It is possible to predict that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle F = -T \ln{<e^{-\beta H}>}} in the new system is a different mathematical function than in the old. For instance, call the new variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} . Then in general we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle F = F(V,T,\psi)}
We calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle F = F(V,T)}
by appending to this the equilibrium condition
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \frac{\partial F}{\partial \psi} = f = 0 }
where f is the generalized force variable (like the magnetic field H) corresponding to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \psi} . Above the critical temperature Tc, this is satisfied by symmetry; below, it is nontrivial. Then from the las two equations the result is a new function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle F'(V,T) } , which is not analytic at Tc. This is Landau's essential insight.
In simplest terms, it is quite clear that the First Theorem requires that F have a boundary of singularities between the two regimes of symmetry, and that therefore analytic continuation between the two is not possible.
Generalized "rigidity"
When we move one end of a ruler, the other moves the same distance, such action at a distance is not built into the laws of nature except in the case of the long-range forces such as gravity or electrostatics. It is strictly a consequence of the fact that the energy is minimized when symmetry is broken in the same way throughout the sample: the phase and angle variables want to be uniform, so that the orientation and position of the lattice is the same everywhere. Of course, in general they are not quite the same, since the lattice can deform elastically, but nonetheless the lattice transmits that force from one end to the other even in equilibrium and without having to flow constantly like a viscous liquid. To break down the rigidity completely, we must supply the condensation energy of a macroscopic piece of the sample, which is very large.
The generalization of this concept to all of the instances of broken symmetry is it call here generalized rigidity. For instance, permanent magnets are so because the magnetization cannot change a little at a time. Superconductivity is the phase rigidity of the electron pair fluid.
In general, there is a rigidity or elastic constant associated with every phase transition to a state with broken continuous symmetry, which prevents the new state from being destroyed by thermal fluctuations. For example, a liquid has no associated rigidity; a nematic phase has an associated rotational elastic constant; a smectic phase has an associated layer modulus; a crystal has an associated shear modulus; a heisenberg magnet has an associated spin-wave stiffness; a superfluid has an associated superfluid density. There are all properties which act to preserve a broken symmetry.
Defect structures
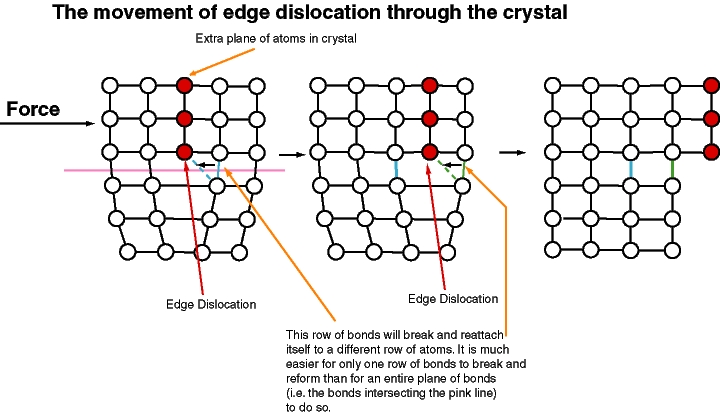
There is a general rule that the breakdown of the generalized rigidity property, along with the resulting dissipation, is a consequence of the formation and motion of defect structures which are usually macroscopic in size.
The twin models for such effects are the domain theory of ferromagnetism, due to Landau (1941), Block (1930) and others, and the dislocation theory of G. I. Taylor (1934), Burgers (1939, 1940), and others. These two cases demonstrate nicely the one general statement which will be justified by the topological theory: that a one-dimensional order parameter allows only two-dimensional ("wall") defects; and that a two-dimensional order parameter allows linear defects such as dislocations, but not necessarily always; while a three- or more- dimensional case may allow point defects.
Clearly in any broken-symmetry system we can imagine forces which would disorient the order parameter in one region relative to another. As a simple example could be that different parts of the sample may have grown with different order parameters and eventually meet in the middle. In what ways can the system respond?
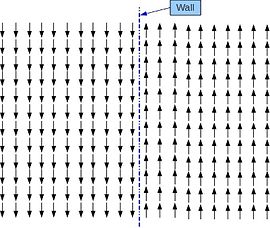
The most obvious and simplest is a boundary or "domain wall" (see right figure): one simply has two or more regions. each locally homogeneous, separated by boundaries. In the case of the one-dimensional order parameter, there is only a discrete set of local equilibrium states (directions of M for a ferromagnet, for instance, or of P for ferroelectric), and there must be a two-dimensional boundary (for a 3D sample) shape of the boundary or other singularity is determined by competition between the forces of generalized rigidity. In the boundary case, characteristically the wall is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx}
one lattice constant thick-- essentially, there is no length parameter except the fundamental microscopic length. Thin boundaries cannot move continuously in space --they are located at a specific crystal plan and must overcome an activation energy to move to the next.
In general, the response to external forces tending to twist or reverse the magnetization must in the first instance come from the motion of these boundaries. To make a permanent magnet, one can proceed in two ways: either to pin the existing boundaries, i.e., to make a very impure material, or to remove them, i.e., to make i of very small particles. Thus the response properties of magnets are wholly conditioned by the defect structures. This is, in fact, the general case.
A second type of defect is a line defect. An example is the dislocation (see next figure). We can imagine following a closed path through a crystal along which the local phase varies gradually, corresponding to a small local strain, but then returns to the original phase changed by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle 2\pi}
. There must be associated a line of singularity where the lattice structure is essentially destroyed.
The two basic types of dislocations are edge dislocations, where an extra plane of atoms has been interpolated ending at a line singularity; and screw dislocations, where the lattice has the topology of a screw.
The easiest way in which a crystal can continuously slide against itself is by the continuous flow of dislocations across a line between the two. Again, there are two ways to make a strong crystal: the easy way is to pin the dislocations, one version of which is called work hardening; the hard way is to eliminate them altogether as in a "whisker" crystal.
Goldstone's Theorem
In this section, we demonstrate what is known as the Goldstone's Theorem, which shows how the emergence of long-range correlations arises as a generic feature of broken continuous symmetry.We concentrate on the form of the spin-spin correlation function: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\alpha \alpha }(\mathbf{x})=<\phi _{\alpha }(\mathbf{x})\phi _{\alpha }(\mathbf{0})>-<\phi _{\alpha }(\mathbf{x})><\phi _{\alpha }(\mathbf{0})>} Technically, it can be evaluated by taking functional derivatives of the functional :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F[j]=ln Z[j]}
as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\alpha \alpha }(\mathbf{x-y})=\frac{\delta ^{2}}{\delta j_{\alpha }(\mathbf{x})\delta j_{\alpha }(\mathbf{y})}F[j]}
We note that for an isotropic system, correlations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\alpha \beta }(\mathbf{x})} with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha \neq \beta } vanish by symmetry. Consider a system with continuous symmetry (n>1), in the ordered phase, and imagine applying a small external field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{a}(\mathbf{x})} . Since the system is assumed to be isotropic, the partition function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z[j]} , which is a scalar quantity, must be independent of the direction of the order parameter.It will, therefore remain unchanged if we perform an infinitesimal rotation of the field direction by an angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \theta } in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\beta ,\gamma )} plane.Only the components Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{\beta }(\mathbf{x})} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{\gamma }(\mathbf{x})} are affected.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{\beta }^{'}(\mathbf{x})=j_{\beta }(\mathbf{x})-\delta \theta j_{\gamma }(\mathbf{x})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{\gamma }^{'}(\mathbf{x})=j_{\gamma }(\mathbf{x})-\delta \theta j_{\beta }(\mathbf{x})}
The variation of F[j] leads to:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0=\int d\mathbf{x}[\frac{\delta F}{\delta j_{\beta }(\mathbf{x})}j_{\gamma }(\mathbf{x})-\frac{\delta F}{\delta j_{\gamma }(\mathbf{x})}j_{\beta }(\mathbf{x})]}
Taking another variation with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{\gamma }(\mathbf{y})}
gives
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0=\int d \mathbf{x}[\frac{\delta ^{2}F}{\delta j_{\beta }(\mathbf{x})\delta _{\gamma }(\mathbf{y})}j_{\gamma }(\mathbf{x})-\frac{\delta ^{2}F}{\delta j_{\gamma }(\mathbf{x})\delta j_{\gamma }(\mathbf{y})}j_{\beta }(\mathbf{x})+\frac{\delta F}{j_{\beta }(\mathbf{x})}\delta (\mathbf{x-y})]}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\int d\mathbf{x}[G_{\beta \gamma }(\mathbf{x-y})j_{\gamma }(\mathbf{x})-G_{\gamma \gamma }(\mathbf{x-y})j_{\beta }(\mathbf{x})+\phi _{\beta }(\mathbf{x})\delta (\mathbf{x-y})]}
Now, let us assume that the initial field was a function in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta } direction, i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{\alpha }(\mathbf{x})=j\delta _{\alpha ,\beta }\; \mathrm{and}\; \phi _{\alpha }=\phi \delta _{\alpha ,\beta }} . In this case, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{\gamma }(\mathbf{x})=0} and we conclude that,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi =\int d\mathbf{x}G_{\gamma \gamma }(\mathbf{x-y})j}
or in the momentum space:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\gamma \gamma }(\mathbf{q=0})=\phi /j}
Since, we are in the ordered phase, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi \rightarrow const.} when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j\rightarrow 0,} and we conclude
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\gamma \gamma }(\mathbf{q=0})=\infty !}
As Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\gamma \gamma }(\mathbf{q=0})} is an even function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{q}} (by inversion symmetry), the most natural possibility is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\gamma \gamma }(\mathbf{q}=0)\sim 1/q^{2}}
We note that the direction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma } can be chosen to be any of the transversal directions to the ordering vector direction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta } .The corresponding correlation function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\gamma \gamma }(\mathbf{q=0})=G_{\perp }(\mathbf{q=0})} thus described the transverse correlations, which we find to be long-ranged:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\perp }(\mathbf{x})\sim \frac{1}{\left | \mathbf{x} \right |^{d-2}}}
This arguement is completely general. It applies to any model with broken continuous symmetry, classical or quantum, and is also valid at any temperature throughout the ordered phase.The excitations associated to these transverse fluctuations are called Goldstone modes or in quantum systems as Goldstone bosons.
Reference: From Dr. Vladimir Dobrosavljevic's class notes on 'Quantum Phase Transitions'.
Collective excitations
The Hamiltonian describing the internal interactions in a macroscopic system still obeys the initial transformations of the symmetry group. The state, however, does not. Immediate consequences of this are
A) Elementary collective excitations of the system, whose character can be determined largely from information about the details of the Hamiltonian and the broken symmetry.
B) There exist new static properties in the broken-symmetry phase that we can call generalized "rigidity". (Described in detail above)
C) Order parameter defects. (Described in detail above)
There are two cases of consequence A:
Case 1) The new broken symmetry state is an eigenstate of the Hamiltonian. (The order parameter is a constant of the motion).
e.g. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -J\sum_{<i,j>}\vec{S_i}\cdot\vec{S_j} } : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle < \vec{S_{tot}} > \neq 0 } in ground state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S_{tot}} = \sum_{i=1}^{N}\vec{S_i} }
Case 2) The new broken symmetry state is not an eigenstate of the Hamiltonian. (The order parameter is not a constant of the motion).
e.g. A crystal cannot be an eigenstate of the Hamiltonian. Positions are fixed, and thus will not commute with the kinetic energy operator.
In Case 1) Spin waves disperse quadratically with momentum, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \omega \propto k^2 } In Case 2) Spin waves disperse linearly with momentum, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \omega \propto k }
There tend to be more examples of case 2, such as crystals, antiferromagnets, nematics (liquid crystals), etc.
Phonons
At low enough temperatures, a system of particles occupies a ground state that does not display the full symmetries of the Hamiltonian. Important and interesting properties of matter appear as elementary excitations and fluctuations of this symmetry breaking ground state.
The low energy excitations of of the crystaline ground state are vibrational modes or phonons. A phonon is a description of a special type of vibrational motion, in which a lattice uniformly oscillates at the same frequency i.e. normal modes. Thereby, phonon is a quantum notion of normal modes. These normal modes are important because any arbitrary lattice vibration can be considered as a superposition of these elementary vibrations.
The name phonon comes from the Greek word φωνή (phonē), which translates as sound, because long-wavelength phonons give rise to sound.
To learn more about these vibrational excitations, consider the following Hamiltonian whose ground state is a cubic crystal:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H} = \sum_{j=1}^N {p_j^2 \over 2m} + \sum_{i>j}V (\mathbf{r_i} -\mathbf{r_j})\ } .
We will make two assumptions:
1. The mean equilibrium position of each ion is a Bravais lattice site ([http://en.wikipedia.org/wiki/Bravais_lattice). With each ion we associate a particular Bravais lattice site R, about which the ion oscillates.
2. The typical displacement of each ion from its equilibrium position are small compared with the interionic spacing.
Assumption 1 makes sure a Bravais lattice exists in spite of ionic motion. The lattice describes the average ionic configuration rather than the instantaneous one. One thing to be remembered, although this assumption permits a wide range of possible ionic motion, is that it does not allow for ionic diffusion: The oscillation of each ion are assumed to be forever about a particular lattice.
Assumption 2 will give rise the harmonic approximation: the expansion in the displacement up to second order only. The results obtain in the harmonic approximation are often in agreement with observed properties of solid. But, some properties still can not be explained by harmonic theory, and one has to go to anharmonic theory (higher order in the expansion in displacements) to account for those properties.
Using assumption 1, we denote the position of the ion whose mean position is R by r(R). In reality, r(R) will deviate from its average value R, and at any given time we can write:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}(\mathbf{R})=\mathbf{R}+\mathbf{u}(\mathbf{R})} ,
where u(R) is the deviation from equilibrium of the ion whose equilibrium site is R. In a cubic lattice
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}=a(l\hat{x}+m\hat{y}+n\hat{z})} ,
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle a} is lattice constant and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle l,m,n} are integers.
A pair of atoms separated by r contributes an amount of potential energy U(r). We can write
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=\frac{1}{2}\sum_{RR'}V(\mathbf{r(R)-r(R')})=\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'+u(R)-u(R')})} .
to make the dependence of the potential energy on the dynamical variables u(R) explicit.
For kinetic energy term, we rewrite
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{p}_{j}\rightarrow \mathbf{p(R)} } .
The Hamiltonian then reads:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{H} = \sum_{R}{p(\mathbf{R})^{2} \over 2M}+\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'+u(R)-u(R')})} .
Assumption 2 now allows us to make the harmonic approximation, based on the expectation that the atoms will not deviate substantially from their equilibrium positions. First we expand the potential energy V about its equilibrium position using Taylor's expansion,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\mathbf{r+a})=f(\mathbf{r})+\mathbf{a}\cdot\nabla f(\mathbf {r})+\frac{1}{2!}(\mathbf{a}\cdot\nabla)^{2}f(\mathbf{r})+\frac{1}{3!}(\mathbf{a}\cdot\nabla)^{3}f(\mathbf{r})+...} .
Applying this expansion to each term in the potential energy, with r = R - R' and a = u(R) - u(R'), we get
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{1}{2}\sum_{RR'}V(\mathbf{R-R'+u(R)-u(R')})=&\underbrace{\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'})}_{U^{eq}}+\underbrace{\frac{1}{2}\sum_{RR'}(\mathbf{u(R)-u(R')}) \cdot\nabla V(\mathbf{R-R'})}_{=0}\\ &+\underbrace{\frac{1}{4}\sum_{RR'}[(\mathbf{u(R)-u(R')})\cdot\nabla]^{2}V(\mathbf{R-R'})}_{U^{harm}}+\underbrace{\text{terms in higher order in } \mathbf{u(R)}}_{U^{anharm}}\\ \end{align}}
The coefficient of u(R) in the linear term above is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{R'}\nabla V(\mathbf{R-R'})} .
This is just minus the force exerted on the atom at R by all other atoms, when each is placed at its equilibrium position. Therefore, it must vanish because there is no net force on atoms in equilibrium.
The harmonic approximation consists in dropping all terms beyond second order in u(R), or else neglecting the terms in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{anharm} } .
Within this approximation, we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle U=U^{eq}+U^{harm}} ,
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{eq}=\frac{1}{2}\sum_{RR'}V(\mathbf{R-R'})}
and
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{harm}=\frac{1}{4}\sum_{\mathbf{RR'}}[\mathbf{u_{\mu}(R)-u_{\mu}(R')}]\phi_{\mu \nu}[\mathbf{u_{\nu}(R)-u_{\nu}(R')}]} ,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\mu \nu}(\mathbf{r})={\partial^{2}V(\mathbf{r})\over \partial r_{\mu}\partial r_{\nu}}}
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle U^{eq}} is just a constant (i.e., independent of the u's and P's), it can be ignored in many dynamical problems, and one frequently acts as if the total potential energy were just Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle U^{harm}} , dropping the superscript altogether when no ambiguity is likely to result.
The harmonic approximation is the starting point for all theories of lattice dynamics. Anharmonic corrections to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle U} , especially those of third and fourth order in the u's, are of considerable importance in understanding many physical phenomena. They are generally treated as small perturbations on the dominant harmonic term.
The harmonic potential energy is usually written in the more general form
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U^{harm}=\frac{1}{2}\sum_{\mathbf{RR'}}u_{\mu}(\mathbf{R})D_{\mu \nu}(\mathbf{R-R'})u_{\nu}(\mathbf{R'})}
with
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{\mu \nu}(\mathbf{R-R'})=\delta_{\mathbf{R,R'}}\sum_{\mathbf{R''}}\phi_{\mu \nu}(\mathbf{R-R''})-\phi_{\mu \nu}(\mathbf{R-R'})} .
Then, the harmonic Hamiltonian becomes
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^{harm}=\sum_{\mathbf{R}}\frac{1}{2M}p(\mathbf{R})^{2}+\frac{1}{2}\sum_{\mathbf{RR'}}u_{\mu}(\mathbf{R})D_{\mu \nu}(\mathbf{R-R'})u_{\nu}(\mathbf{R'})}
We will extract the eigenvalues from this Hamiltonian. Later, we will find that the energy due to lattice vibration of an N-ion harmonic crystal can be be obtained as the sum over 3N discrete normal modes. These discrete normal modes or quasi-particles are called phonons.
We proceed as follows: Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s(\mathbf{k})} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon}_s(\mathbf{k})} be the frequency and polarization vector for the classical normal mode with polarization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle s} and wave vector k. Now define the "phonon annihilation operator":
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\mathbf{k}s}=\frac{1}{\sqrt{N}}\sum_{\mathbf{R}}e^{-i\mathbf{k\cdot R}}\mathbf{\epsilon}_{s}(\mathbf{k})\cdot \left[\sqrt{M\omega_s(\mathbf{k})\over 2\hbar}\mathbf{u(R)}+i\sqrt{1 \over 2\hbar M\omega_s(\mathbf{k})}\mathbf{p(R)}\right]} ,
and its adjoint, the "phonon creation operator":
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^{\dagger}_{\mathbf{k}s}=\frac{1}{\sqrt{N}}\sum_{\mathbf{R}}e^{-i\mathbf{k\cdot R}}\mathbf{\epsilon}_{s}(\mathbf{k})\cdot\left[\sqrt{M\omega_s(\mathbf{k})\over 2\hbar}\mathbf{u(R)}-i\sqrt{1 \over 2\hbar M\omega_s(\mathbf{k})}\mathbf{p(R)}\right]} .
The canonical commutation relations,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [u_\mu (\mathbf{R}),p_\nu (\mathbf{R'})]=i\hbar\delta_{\mu\nu}\delta_\mathbf{R,R'}} ,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [u_\mu (\mathbf{R}),u_\nu (\mathbf{R'})]=[p_\mu (\mathbf{R}),p_\nu (\mathbf{R'})]=0} ,
the identity
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_\mathbf{R}e^{i\mathbf{k\cdot R}}=\begin{cases}0,\quad\quad\quad&\mathbf{k}\quad \text{is not a reciprocal lattice vector},\\ N,&\mathbf{k}\quad \text{is a reciprocal lattice vector},\end{cases}}
and the orthonormality of polarization vectors
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon_s(k)\cdot\epsilon_{s'}(k)}=\delta_{ss'}, \quad \quad s,s'=1,2,3}
yield the commutation relations
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}&[a_{\mathbf{k}s},a^\dagger_{\mathbf{k'}s'}]=\delta_\mathbf{kk'}\delta_{ss'},\\ &[a_{\mathbf{k}s},a_{\mathbf{k'}s'}]=[a^\dagger_{\mathbf{k}s},a^\dagger_{\mathbf{k'}s'}]=0.\end{align}}
Now one can express the coordinates and momenta in terms of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\mathbf{k}s}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^\dagger_{\mathbf{k'}s'}} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}&\mathbf{u(R)}={1 \over \sqrt{N}}\sum_{\mathbf{k}s}\sqrt{\hbar \over 2M\omega_s(\mathbf{k})}(a_{\mathbf{k}s}+a^\dagger_{\mathbf{-k'}s'})\mathbf{\epsilon}_s(\mathbf{k})e^{i\mathbf{k\cdot R}},\\ &\mathbf{p(R)}={1 \over \sqrt{N}}\sum_{\mathbf{k}s}\sqrt{\hbar M\omega_s(\mathbf{k})\over 2}(a_{\mathbf{k}s}-a^\dagger_{\mathbf{-k'}s'})\mathbf{\epsilon}_s(\mathbf{k})e^{i\mathbf{k\cdot R}}.\end{align}}
Equation above can be obtained by substitution of equations for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\mathbf{k}s}}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^\dagger_{\mathbf{k'}s'}}
, and by use of the "completeness relation" that holds for any complete set of real orthogonal vectors,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{s=1}^3[\mathbf{\epsilon}_s(\mathbf{k})]_\mu[\mathbf{\epsilon}_s(\mathbf{k})]_\nu=\delta_{\mu\nu},}
together with identity
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_\mathbf{k}e^{i\mathbf{k.R}}=0,\quad\quad \mathbf{R}\neq 0.}
Having expressed u(R) and p(R) in terms of annihilation and creation operators, we can also write the harmonic Hamiltonian in terms of the new operators. It can be shown that the kinetic energy is given by:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {1 \over 2M}\sum_\mathbf{R}\mathbf{P(R)}^2=\frac{1}{4}\sum_{\mathbf{k}s}\hbar\omega_s(\mathbf{k})(a_{\mathbf{k}s}-a^\dagger_{\mathbf{-k'}s'})(a^\dagger_{\mathbf{k}s}-a_{\mathbf{-k'}s'}).}
Next, we define the dynamical matrix D(k)
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{D(k)}=\sum_\mathbf{R}\mathbf{D(R)}e^{-i\mathbf{k\cdot R}}.}
Now let the polarization vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon}_s(\mathbf{k})} be the eigenvectors of the dynamical matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{D(k)}} ,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\omega^2\mathbf{\epsilon}=\mathbf{D(k)}\mathbf{\epsilon}.}
Using these facts, we can write the potential energy as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=\frac{1}{4}\sum_{\mathbf{k}s}\hbar\omega_s(\mathbf{k})(a_{\mathbf{k}s}+a^\dagger_{\mathbf{-k'}s'})(a^\dagger_{\mathbf{k}s}+a_{\mathbf{-k'}s'}).}
Adding the kinetic and potential terms together, we get that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H={1 \over 2}\sum \hbar \omega_s(\mathbf{k})(a_{\mathbf{k}s}a^\dagger_{\mathbf{k}s}+a^\dagger_{\mathbf{k}s}a_{\mathbf{k}s}),}
and, using the commutation relations, we find that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum \hbar \omega_s(\mathbf{k})(a^\dagger_{\mathbf{k}s}a_{\mathbf{k}s}+{1 \over 2}).}
This is nothing more than the sum of 3N independent oscillators, one for each wave vector and polarization. When a Hamiltonian is divided into a sum of commuting sub-Hamiltonians, its eigenstates are simply all products of the eigenstates of sub-Hamiltonians, and the eigenvalues are the sum of the individual eigenvalues of the sub-Hamiltonians. We can therefore specify an eigenstate of H by giving a set of 3N quantum numbers Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{\mathbf{k}s}}
, one for each of the 3N independent oscillator Hamiltonians Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar\omega_s(\mathbf{k})(a^\dagger_{\mathbf{k}s}a_{\mathbf{k}s}+{1 \over 2})}
. The energy of such a state is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=\sum\left(n_{\mathbf{k}s}+{1 \over 2}\right)\hbar\omega_s\mathbf{(k)}.}
In this description the independent oscillators that give rise to normal modes can be regarded as quasiparticles, i.e. phonons.
Below we give an example of normal modes (phonons) of a monoatomic 3D bravais lattice with short ranged interactions. The main purpose in this case is to seek the dispersion relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(\mathbf{k})} .
We begin with 3N equations of motion (since we have N ions in 3D):
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\ddot{u}_\mu(\mathbf{R})= -{\partial U^{harm}\over \partial u_\mu (\mathbf{R})}= -\sum_{\mathbf{R'\nu}}D_{\mu\nu}(\mathbf{R-R'})u_\nu(\mathbf{R'}), }
or in matrix notation,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\ddot{u}_\mu(\mathbf{R})=-\sum_{\mathbf{R'}}D(\mathbf{R-R'})u(\mathbf{R'}). }
We are looking for solutions in the form of simple plane waves:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u(R,t)}=\mathbf{\epsilon}e^{i(\mathbf{k\cdot R}-\omega t)} }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon}}
is the polarization vector of the normal mode mentioned above.
We continue to use the periodic boundary condition which is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{u(R}+N_ia_i)=\mathbf{u(R)} }
for each of the three primitive vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle a_i}
, where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle N_i}
are large integers satisfying
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle N=N_1N_2N_3. }
This restricts the allowed wave vectors k to
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}={n_1\over N_1}\mathbf{b_1}+{n_2\over N_2}\mathbf{b_2}+{n_3\over N_3}\mathbf{b_3} }
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i}
integral and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{b_i}}
are the reciprocal lattice vectors satisfying Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{b_i\cdot a_j}=2\pi \delta_{ij}}
. Generally, it is convenient to take crystal cell to be in the first Brillouin zone.
With the assumption that the solutions are in the simple planewave vectors form, the equation of motions become eigenvalue problems, i.e.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\omega^2\mathbf{\epsilon}=\mathbf{D(k)\epsilon} }
D(k) is the dynamical matrix defined above. The three solutions to equation above for each of the N allowed value of k, give 3N normal modes. We manipulate D(k), using the property that the interaction is short ranged and only nearest neighbour contributions survive:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{D(k)}&={1 \over 2}\sum_\mathbf{R}\mathbf{D(R)}[e^{-i\mathbf{k\cdot R}}+e^{i\mathbf{k\cdot R}}-2]\\ &=\sum_\mathbf{R}\mathbf{D(R)}[cos(\mathbf{k\cdot R})-1]\\ &=-2\sum_\mathbf{R}\mathbf{D(R)}sin^2 \left({1\over 2}\mathbf{k\cdot R}\right).\\ \end{align}}
Equation above explicitly demonstrate that D(k) is an even function of k and a real matrix. It can be further shown that D(k) is a symmetric matrix. One theorem in matrix algebra states that every real symmetric 3D matrix has three real eigenvectors, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon_1, \epsilon_2, \epsilon_3}}
which satisfy
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{D(k)\epsilon_s (k)}=\lambda_s \mathbf{(k)\epsilon_s(k)} }
Evidently the three normal modes with wave vector k will have polarization vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon}_s(\mathbf{k})}
and frequencies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s\mathbf{(k)}}
given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s(\mathbf{k})=\sqrt{{\lambda_s\mathbf{(k)}\over M}} }
To determine the k dependence of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s}
at small k, we have to remember when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k\cdot R}}
is small for all R connecting sites whose ions have any appreciable interaction, then we can approximate the sine in dynamical matrix equation by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sin^2 \left({1\over 2}\mathbf{k\cdot R}\right)\approx \left({1\over 2}\mathbf{k\cdot R}\right)^2, }
therefore
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{D(k)}\approx -{k^2 \over 2}\sum_R\mathbf{(\hat{k}\cdot R)^2 D(R)}. }
Consequently, in the long-wavelength or small k limit, we can write
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s(\mathbf{k})=c_s(\mathbf{\hat{k}})k, }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_s(\mathbf{\hat{k}})}
are the squqre roots of the eigenvalues of the matrix
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -{1 \over 2}\sum_R\mathbf{(\hat{k}\cdot R)^2 D(R)}. }
So, the dispersion relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s(\mathbf{k})}
is linear in the long-wavelength limit. This is a result of the approximation of short-ranged interaction! For long-ranged interaction, such as the Coulomb inteaction, the dispersion relation would differ. However, it is guaranteed that so-called "soft modes", with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(\mathbf{k}) \to 0 }
as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |k| \to 0 }
, exist. These modes are the Goldstone-modes corresponding to the broken translational symmetries.
In 3D, it is important to consider not only the behavior of the frequencies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_s(\mathbf{k})} but also the relation between the direction of polarization Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\epsilon}_s(\mathbf{k})} and the direction of propagation k. In an isotropic medium, we can always choose the three solutions for a given k so that one branch (the longitudinal branch) is polarized along the direction of propagation and the other two transverse branches are polarized perpendicular to the direction of propagation. In an anisotropic crystal the polarization vectors need not be simply related to the direction of propagation unless k i invariant under certain symmetry of the crystal.
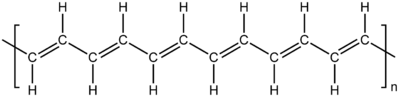
Spin Waves and the Heisenberg Ferromagnet
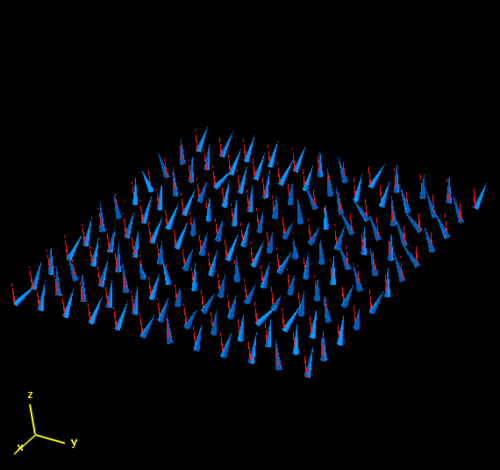
Spin waves (also called magnons) are the classical normal modes or collective quantum excitations of a magnetically ordered system. The projection of spin on an atom is reduced by one, but the excitation is not localized and propagates in the form of a wave throughout the lattice. In the long-wavelength limit, spin waves are the hydrodynamic modes related to the broken symmetry resulting from alignment (or anti-alignment) of the spins. For an antiferromagnet, spin waves have the dispersion relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega \propto q } and for a ferromagnet, spin waves have the dispersion relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega \propto q^2 } .
Spin waves can be derived by constructing a low lying excited state to an ordered ferromagnet. Assuming a cubic lattice, we can write the Hamiltonian for the isotropic (Heisenberg) ferromagnet as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S(R) \vec S(R') }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle J(R - R') } is short ranged, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle J > 0 } . The ground state occurs when all of the spins are aligned. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |S\rangle } is the maximum spin projection, then the ground state is : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0 \rangle = \prod_R |S\rangle_R}
Trying to lower a single spin to create an excited state eigenstate does NOT produce an eigenstate. For example, we can create a state which is the same as the ground state, except the spin at R has been lowered:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |R_0\rangle = \frac{1}{\sqrt{2S}}S^{-}(R)|0\rangle }
However, the Hamiltonian will flip the spin at R back up, and then flip another spin at R' down. First we rewrite the Hamiltonian, using the relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{\pm}(R) = S^x(R)\pm iS^y(R)} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S(R) \vec S(R') }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^z(R) \vec S^z(R') - \frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^x(R) \vec S^x(R') -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^y(R) \vec S^y(R') }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^z(R) \vec S^z(R') - \frac{1}{2}\sum_{R\neq R'} J(R - R')S^{-}(R')S^{+}(R) }
Now examine how this Hamiltonian acts on our proposed state:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H|R_0\rangle = -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^z(R) \vec S^z(R')|R_0\rangle - \frac{1}{2}\sum_{R\neq R'} J(R - R')S^{-}(R')S^{+}(R)|R_0\rangle }
The first term (ignoring constants):
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec S^z(R) \vec S^z(R')|R_0\rangle = \vec S^z(R) \vec S^z(R')\vec S^-(R_0)|0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \vec S^z(R)\left( \left[S^{z}(R'),S^{-}(R_0) \right] + \vec S^{-}(R_0)\vec S^z(R') \right) |0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \vec S^z(R) \left( -S^{-}(R_0)\delta_{R',R_0} + S S^{-}(R_0) \right) |0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \delta_{R,R_0}\delta_{R',R_0}S^{-}(R_0)|0\rangle - S\delta_{R',R_0}S^{-}(R_0)|0\rangle - S\delta_{R,R_0}S^{-}(R_0) + S^2S^{-}(R_0)|0\rangle }
Now returning the constants: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{1}{2}\sum_{R\neq R'} J(R - R')\vec S^z(R) \vec S^z(R')|R_0\rangle = \frac{S}{2}\sum_{R\neq R'} J(R - R_0)|R_0\rangle + \frac{S}{2}\frac{S}{2}\sum_{R\neq R'} J(R_0 - R')|R_0\rangle - \frac{S^2}{2}\sum_{R\neq R'} J(R - R')|R_0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = S\sum_{R\neq R'} J(R - R')|R_0\rangle + E_0 }
Where the last term, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle E_0 } , is the ground state energy. So far Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |R_0\rangle } appears to be an eigenstate of the Hamiltonian. However, we much still examine the second term:
The second term: (ignoring constants)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{-}(R')S^{+}(R)|R_0\rangle = S^{-}(R')S^{+}(R)S^{-}(R_0)|0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = S^{-}(R')\left[S^+(R),S^-(R_0) \right]|0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = S^-(R')\left(2S^z(R)\delta_{R,R_0} \right)|0\rangle = 2S\delta_{R,R_0}S^{-}(R')|0\rangle }
Now returning the constants:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}\sum_{R\neq R'} J(R - R')S^{-}(R')S^{+}(R)|R_0\rangle = -S\sum_{R\neq R'} J(R - R')\delta_{R,R_0}|R'\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-S\sum_{R\neq R_0} J(R_0 - R)|R\rangle }
Therefore, we have:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H|R_0\rangle = E_0|R_0\rangle + S\sum_{R\neq R_0} J(R_0 - R)\left(|R_0\rangle - |R\rangle\right) }
Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |R_0\rangle} is not an eigenstate of the Hamiltonian. Although Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |R_0\rangle } is not an eigenstate, it is a linear combination of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |R_0\rangle } and other states with one lowered spin.
So we must continue to seek and excited state eigenstate. Because J depends on R and R' only in a translationally variant combination, we can seek eigenstates of the form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec k \rangle = \frac{1}{\sqrt{N}}\sum_R e^{i \vec k \cdot \vec R }|R_0\rangle }
This makes a superposition of phase factors of states where only one spin is flipped. Applying the Hamiltonian to this state yields:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H|\vec k \rangle = E_0|\vec k \rangle + \frac{S}{\sqrt{N}}\sum_{R\neq R'} J(R - R') \left( e^{i\vec k \cdot \vec R }|R'\rangle - e^{i\vec k \cdot \vec R'}|R\rangle\right) } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = E_0|\vec k \rangle + S\sum_{R} J(R - R')|\vec k \rangle - \frac{S}{\sqrt{N}}\sum_{R}\left( \sum_{R'}e^{i\vec k \cdot (\vec R' - \vec R) } J(R - R')|R\rangle \right) e^{i\vec k \cdot \vec R} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = E_0|\vec k \rangle + S\sum_{R} J(R - R')\left(1 - e^{i\vec k \cdot (\vec R - \vec R') } \right)|\vec k \rangle } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = E_0|\vec k \rangle + S\left(\sum_{R} J(R)(1 - e^{i\vec k \cdot (\vec R) } )\right)|\vec k \rangle }
since we can write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{R} J(R)\left(1 - e^{i\vec k \cdot \vec R } \right) = 2\sum_{R} J(R) \sin^2\left(\frac{\vec k \cdot \vec R}{2}\right) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec k) = E_0 + 2S\sum_{R} J(R) \sin^2\left(\frac{k \cdot R}{2}\right) }
For small k, this has dependence on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle k^2 }
. And so we have the k dependence of the energy dispersion for one spin-wave mode at wave vector k for an isotropic ferromagnet. For additional spin waves an interaction term must be included due to the scattering of spin waves off one-another.
Spin Waves and Magnetization
The energy dispersion of the spin waves can be used to find the low-T behavior of the magnetization M(T). To do this, the ferromagnetic spin waves are treated as a non-interacting gas of bosons. Since a spin wave is a delocalized flip of a spin, each spin wave lowers the magnetization by one unit.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(T) = NS - \sum \frac{1}{\exp(\beta \epsilon) - 1} }
where the second term is the total number is spin waves at temperature T, with (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = \frac{1}{k_B T} } ).
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M(T) = M(0)\left( 1 - \frac{V}{NS}\int \frac{d^3k}{(2\pi)^3} \frac{1}{\exp(\beta \tilde{\epsilon}) - 1}\right) }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle M(0) = NS} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \tilde{\epsilon} = 2S\sum_{R}J(\vec R) \sin^2 \left(\frac{\vec k \cdot \vec R}{2}\right) } . Since we're looking for low - T asymptotics we expand this, using the approximation that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle\tilde{\epsilon} = Vk^2 } where V is some constant.
Spin Wave (SW) Theory
The spin-wave theory, due originally to Anderson, which is widely used to obtain results for many different systems, gives results for the energies of the elementary excitations or spin waves. The method works for both ferromagnets and antiferromagnets, it works in 2D and 3D as well as 1D, and it works for arbitrary spin – not just for spin-1/2. The ferromagnetic version is rather simple and the results are usually exact. The antiferromagnetic version is more complicated and the results are approximate. However,these results are still in reasonable correspondence with exact results.The basic idea of spin-wave theory is to replace the spin operators by bosons. As we have seen, spin operators behave like fermions on a given site, but like bosons where different sites are concerned.
For a general spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} and a single site the corresponding basis is again the eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{z}} written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |m\rangle} where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2S+1} values of m are
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m = -S,-S+1,-S+2,...,S}
and the states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |m\rangle} are orthogonal and normalized (i.e. orthonormal). Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S-m} be the number of deviations from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |S\rangle} ,the state of maximum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{z}} .
Recall the following relations:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{+}|m\rangle = \sqrt{(S-m)(S+m+1)}|m+1\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{-}|m\rangle = \sqrt{(S+m)(S-m+1)}|m-1\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{z}|m\rangle = m|m\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{+}|S\rangle = 0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{-}|-S\rangle = 0}
We now introduce boson operators for a single site which reproduce most of the above properties. There are various ways of doing this but we shall only consider the most useful and widely used, called the Holstein-Primakoff transformation.
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^{+},a} be boson creation and destruction operators, with the usual commutation relations
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left [a_{i},a^{+}_{j}\right ] = \delta_{ij}} etc.
We now interpret the number of bosons as the number of deviations from the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} . State Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} has Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (S-m)} deviations and the number operator for bosons is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n} \equiv a^{+}a} so
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}|m\rangle = a^{+}a|m\rangle = (S-m)|m\rangle}
We can represent Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{z}} as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{z} = S-\hat{n}} , since
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{z}|m\rangle =(S-\hat{n})|m\rangle = [S-(S-m)]|m\rangle}
And
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^{+} = a\sqrt{2S}\sqrt{1-\frac{\hat{n}}{2S}}}
Proof:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{+}|m\rangle = a\sqrt{2S}\sqrt{1-\frac{\hat{n}}{2S}}|m\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sqrt{2S}\sqrt{S-m}\sqrt{1-\frac{\hat{n}}{2S}}|m+1\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sqrt{2S}\sqrt{S-m}\sqrt{1-\frac{(S-m-1)}{2S}}|m+1\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sqrt{S-m}\sqrt{2S-s+m+1}|m+1\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \sqrt{(S-m)(S+m+1)}|m+1\rangle}
Similarly for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S}
Note that the Holstein-Primakoff transformation is exactas far as the states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |S\rangle,|S-1\rangle,...,|-S\rangle } are concerned. However, in principle it is possible to have more than S bosons, i.e. a state of the form
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi\rangle = (a^{+})^{k}|S\rangle} where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k > m}
These states are unphysical and they can never be reached if we use the exact transformation.However, we shall now approximate the transformation and this allows coupling to the unphysical states. The approximation will only be valid provided the admixture of the unphysical states is ‘small’ in some sense. Mathematically it is very difficult to handle a transformation involving square roots. The approximation we shall use is based on the assumption that the states of interest all have small probabilities of having deviations on any particular site and a negligible probability of having two or more deviations on the same site. This is equivalent to saying
1. The total number of deviations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{D} is \ll N} , i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle \hat{n} \right \rangle \ll 1}
2. Bound states in which deviations cluster together cannot be treated accurately.
Under these approximations, we can write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{1-\frac{\hat{n}}{2S}}\approx 1} for simple W theory, and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{1-\frac{\hat{n}}{2S}} \approx 1-\frac{\hat{n}}{4S}}
For simple SW theory we now obtain a very simple result
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{+} \approx \sqrt{2S}a}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{-} \approx \sqrt{2})a^{+}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^{z}=S - a^{+}a}
Ferromagnetic Spin-Wave Theory
Consider the Heisenberg model with nearest neighbour ferromagnetic coupling
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = \frac{J}{2}\sum_{j}\sum_{\rho}\boldsymbol{S}_{j}\boldsymbol{S}_{j+\rho}} where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J < 0} , j runs over all sites, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho} runs over all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} numbers. The ground state is a state with all atoms aligned. Usually we take this to be the state in which all atoms are in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |+S\rangle} state. Other degenerate ground states can be easily constructed from this state by using the lowering operator for the whole system Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i}S_{i}^{-}} . Writing
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{S}_{j}\boldsymbol{S}_{j+\rho} = S_{j}^{z}S_{j+\rho}^{z} + \frac{1}{2}(S_{j}^{+}S_{j+\rho}^{-} + S_{j}^{-}S_{j+\rho}^{+}}
Using the simple SW results, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = \frac{JN\nu}{2}S^{2} - \frac{JS}{2}\sum_{j}\sum_{\rho}(a_{j}^{+}a_{j}+a_{j+\rho}^{+}a_{j+\rho})+\frac{JS}{2}\sum_{j}\sum_{\rho}(a_{j}^{+}a_{j+\rho}+a_{j+\rho}^{+}a_{j})+\frac{J}{2}\sum_{j}\sum_{\rho}(a_{j}^{+}a_{j}a_{j+\rho}^{+}a_{j+\rho})}
The last term here involves four boson operators. For consistency with our previous approximation we must neglect this term. The first term is the energy of the ground state (all N spins up)Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |SSS...S\rangle} . Calling the first term as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{F}} , and using our approximation, we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = E_{F}-\frac{JS}{2}\sum_{j}\sum_{\rho}(a_{j}^{+}a_{j}+a_{j+\rho}^{+}a_{j+\rho}-a_{j}^{+}a_{j+\rho}-a_{j+\rho}^{+}a_{j}}
We go to Fourier space to diagonalize this Hamiltonian. Define
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_{k} = \frac{1}{N}\sum_{j}e^{ikj}a_{j}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_{k}^{+} = \frac{1}{N}\sum_{j}e^{-ikj}a_{j}^{+}}
The reverse transformations are
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{j} = \frac{1}{N}\sum_{j}e^{-ikj}\alpha_{k}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{k}^{+} = \frac{1}{N}\sum_{j}e^{ikj}\alpha_{j}^{+}}
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left [\alpha_{k_{1}},\alpha^{+}_{k_{2}}\right ] = \delta_{k_{1}k_{2}}}
Using this,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = E_{F} + \sum_{k} \epsilon_{k}\alpha^{+}_{k}\alpha_{k}}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{k} = -JS\sum_{\rho}(1-cosk\rho)} . These are the energies relative to the fully alligned ground state of the ferromagnetic spin waves.
A solved problem for spin waves
Hydrodynamics
In principle, many-body systems can be studied microscopically by writing down all the equations of motion but that is practically impossible due to the large number of degree of freedom. Thermodynamics is by far a more practical way to study many-body systems. In this theory, many-body system in equilibrium states can be described macroscopically by a small number of thermodynamic variables (or macroscopic degree of freedom), such as internal energy, temperature, pressure, magnetization, etc. In a system with broken continuous symmetry, the theory can be extended to describe the spatially non-uniform states in which the elastic distortion (small amplitude distortion) from the homogenous states is of long wavelength and slowly varying (low frequency). Because of the long wavelength of the elastic distortion, the departure from homogenous states is small. In this chapter, we will derive the equations governing the dynamics of the system undergoing such kind of distortions based mostly on what we have learned in thermodynamics.
Conserved and broken-symmetry variables
Thermodynamic equilibrium is created and maintained by the collisions between particles. These collisions are characterized by the time interval Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \tau } between two successive collisions experienced by one particle or by its mean free path Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \lambda } which is equal to velocity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle v } times Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \tau } . Now, consider a distortion that oscillates in time and space with frequency Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \omega } and wave number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle q } . If the disturbance has long wavelength and low frequency, i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle q \cdot \lambda \ll 1 } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \omega \cdot \tau \ll 1 } , there will be enough time and space for the collisions to locally equilibrate the system. That is why we can really use thermodynamics to study the system in this situation. Most disturbances in many-body systems have characteristic frequencies that are of the order of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \tau^{-1} } and they decay quickly to equilibrium. There are, however, certain variables that are guaranteed to have slow temporal variations at long wavelength. There are 2 such categories:
- densities of conserved variables, and
- broken symmetry variables
The density of conserved variable such as number density follows the conservation law:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \frac{\partial n}{\partial t} + \nabla \cdot j = 0}
When Fourier transformed, such equation implies that when the frequency goes to zero so does that wave number, because the time derivative brings down a factor of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \omega } in the first term whereas the gradient yields a factor of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle q } in front of the second term. Therefore the disturbances in the densities of conserved variables are guaranteed to have long wavelength and low frequency.
For a system with broken continuous symmetry, spatially uniform changes in elastic variables lead to new equilibrium states that are stationary in time. For example, if we apply a uniform translation on a crystal, it will end up being in the same state as before. Therefore, frequency Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \omega } associated with a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle q = 0 } displacement of continuous broken symmetry elastic variable is also zero. Spatially non-uniform displacement, however, will have non-zero characteristic frequency. Therefore the disturbance in the densities of broken symmetry variables are also guaranteed to have long wavelength and low frequency.
Historically, the dynamics of variables with long wavelength and low frequency was first studied extensively in water. The dynamics of water in motion is called hydrodynamics. Nowadays, the term hydrodynamics is not just limited to water, it is used for long-wavelength and low-frequency dynamics of conserved and broken-symmetry variables in any systems, such as spin systems and liquid crystals, etc.
Planar Ferromagnet
The procedure for deriving hydrodynamic equations is as follows. First, because hydrodynamics is basically a perturbation (small amplitude disturbance of long wavelength and low frequency) from thermodynamic equilibrium, we have to generalize the thermodynamic treatment to include all the conserved and broken-symmetry variables. In the other words, we have to write down the first law of thermodynamics with taking into account those variables. Secondly, we have to identify the reactive or nondissipative couplings, which couples the time derivative of a hydrodynamic variable of one sign to another variable of the opposite sign under the time reversal. Next, we have to derive the irreversible dissipative couplings. Both reactive and dissipative couplings, which relate currents to thermodynamic fields, are called constitutive relations. All that together with conservation law, thermodynamic relations allow us to find out the hydrodynamic equations of the system. That procedure will be illustrated in the planar ferromagnetic system.
A planar ferromagnet is described by the Hamiltonian.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = -\sum_{R, R'} J_{||}(R-R')S^z(R)S^z(R')+J_{\perp}(R-R')\left(S^x(R)S^x(R')+S^y(R)S^y(R')\right) \qquad 0<J_{||}<J_{\perp}}
The hydrodynamic variables of this system at high temperatures (disordered phase) are energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \epsilon} , the total spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^z_{tot}} , both of which are conserved quantities. Let's start with the discussion on the disordered phase.
Disordered Phase
The fundamental thermodynamic relation is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Tds = d \epsilon - h d m_z\,}
The equation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s\left(\epsilon,m_z\right) = s(\epsilon) - \frac{1}{2T}\chi^{-1}m_z^2 \cdots} gives
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Longrightarrow h = -T\frac{\partial s}{\partial m_z} = -\chi m_z} for small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle m_z}
next, we have to introduce the conservation law which is given by the continuity relation for both energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \epsilon\,} and magnetization along the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle z,} direction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle m_z\,}
From the fundamental thermodynamic relation and the conservation law, we get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \quad T\frac{\partial s}{\partial t}=\frac{\partial\epsilon}{\partial t}-h\frac{\partial m_z}{\partial t} = -\nabla \cdot j_\epsilon + h\nabla \cdot j_{m_z}}
which gives,
Next, consider (just mathematical identities) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}& \nabla \cdot \left(\frac{j_\epsilon}{T}\right)&=&\frac{1}{T}\nabla \cdot j_\epsilon - \frac{1}{T^2}(\nabla T \cdot j_\epsilon)\\& \nabla \cdot \left(\frac{hm_z}{T}\right)&=&\frac{h}{T}\nabla \cdot j_{m_z}+\frac{\nabla h}{T}\cdot j_{m_z}-\frac{\nabla T}{T^2}\cdot(h j_{m_z})\end{align}}
which we substitute back into the equation above, so that
which gives
Now, we perform an integration over all volume, and using the Gauss' Theorem keeping in mind that the current vanishes at the surface we get :
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = \int d^3 \vec{r} \ s} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial S}{\partial t} + \underbrace{\int d^3 \vec{r}\ \nabla \cdot\frac{j-\epsilon - h j_{m_z}}{T}}_{= \ 0} = \int d^3 \vec{r} \left(-(\overbrace{j_\epsilon - h j_{m_z}}^{= \ j_Q})\frac{\nabla T}{T^2} - \frac{\nabla h \cdot j_{m_z}}{T}\right)}
At this point, we have to consider whether or not dissipation exist in the system. If it does not exist, then there is no entropy production, hence the term Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial S}{\partial t}}
vanishes as a result Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle j_Q }
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle j_{m_z}}
vanish accordingly. Which make sense because in the system without dissipation, there should be no change in the energy nor magnetization so there is no current for both of them. So :
In the case of dissipation, what we have to consider is how the entropy changes. Our equation above allows the entropy production to be positive or negative, mathematically. Therefore, we impose a constraint that the rate of change for the entropy to be strictly positive in our constitutive relations. We see, that this can be done by setting the integrand to be positive.
Let, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_Q = -\kappa \nabla T}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{m_z} = -\Gamma \nabla h}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \kappa > 0}
is the thermal conductivity and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \Gamma >0}
is just a transport coefficient (or actually we can just say that both are just transport coefficients).
We now see that the rate of change of the entropy becomes
In addition, dissipative currents of one sign under time reversal operation must be proportional to the variables of the opposite sign.
With the constitutive relations above, we rewrite the continuity relations as follows:
Going further, these relations can be closed by using thermodynamic relations
,
which gives us two diffusion equations :
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa / C(m_z)\,}
is the thermal diffusion coefficient and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma / \chi\,}
is the magnetization diffusion coefficient.
Each of these diffusion equations corresponds to one mode. And we see that there is always one mode associated with each conserved variable.
Ordered Phase
The ordered phase of the planar ferromagnet is characterized by an order parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{m}_{||}(\vec{r}) = \left|\vec{m}_{||}(\vec{r})\right|e^{i\theta(\vec{r})} } and to describe it, we need an additional slow/hydrodynamical variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{V}_\theta = \vec{\nabla} \theta} . This additional slow variable modifies the fundamental thermodynamic relation as follows
Therefore, we get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h = -T \frac{\partial s}{\partial m_z} = \frac{m_z}{\chi} + \cdots; \qquad h_\theta = -T \frac{\partial s}{\partial V_\theta} = \rho_s V_\theta + \cdots}
And as before, we address the conservation law in the form of the continuity equation for all conserved variables Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon, m_z, V_\theta\,}
We then take the time derivative of the entropy density : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial s}{\partial t} = -\frac{1}{T}\nabla \cdot j_\epsilon + \frac{h}{T} \nabla \cdot j_{m_z} - \frac{h_\theta}{T} \left(\nabla h + \nabla X'\right)}
And again using the mathematical identities :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} &\nabla \cdot \left(\frac{j_\epsilon}{T}\right) &=& \frac{\nabla \cdot j_\epsilon}{T} - j_\epsilon \frac{\nabla T}{T^2}\\ &\nabla \cdot \left(\frac{h j_{m_z}}{T}\right) &=& \frac{h}{T} \nabla \cdot j_{m_z} + \frac{j_{m_z} \cdot \nabla h}{T} - h j_{m_z} \cdot \frac{\nabla T}{T^2}\\ &\nabla \cdot \left(\frac{h_\theta X'}{T}\right) &=& \frac{h_\theta}{T}\cdot \nabla X' + \frac{\nabla \cdot h_\theta}{T}X' - X' h_\theta \cdot \frac{\nabla T}{T^2} \end{align} }
and substitute them into the equation for the rate of change of the entropy density:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial s}{\partial t} = -\nabla \cdot \left(\frac{j_\epsilon}{T}\right) - j_\epsilon \cdot \frac{\nabla T}{T^2} + \nabla \cdot \left(\frac{h j_{m_z}}{T}\right)-\frac{j_{m_z} \cdot \nabla T}{T} + h j_{m_z} \cdot \frac{\nabla T}{T^2} - \nabla \cdot \left(\frac{h_\theta X'}{T}\right) + \frac{\nabla \cdot h_\theta}{T}X' - X' h_\theta \cdot \frac{\nabla T}{T} - \frac{h_\theta \cdot \nabla h}{T}}
Grouping terms with the same factor and integrating gives :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial S}{\partial t} = \int d^3\vec{r}\ \left[-\overbrace{\left(j_\epsilon - h j_{m_z} + X' h_\theta\right)}^{=j_Q}\cdot \frac{\nabla T}{T^2} - \frac{1}{T}\left(j_{m_z} \cdot \nabla h + h_\theta \cdot \nabla h - X' \nabla \cdot h_\theta\right)\right]}
In the absence of dissipation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial S}{\partial t} = 0} which results in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X' = 0; \qquad j_\epsilon = h j_{m_z}; \qquad j_{m_z} = -h_\theta = -\rho_s V_\theta}
The result from the non-dissipative process above implies
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} & \frac{\partial m_z}{\partial t} &=& \; -\nabla \cdot j_{m_z} = \; \rho_s \nabla \cdot V_\theta\\ & \frac{\partial V_\theta}{\partial t} &=& \; \nabla h =\; \frac{1}{\chi}\nabla m_z \end{align} }
Therefore taking time derivative of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial m_z}{\partial t}} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2 m_z}{\partial t^2} =\; \rho_s \nabla \cdot \frac{\partial V_\theta}{\partial t} =\; \frac{\rho_s}{\chi}\nabla^2 m_z}
or, more explicitly :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla \frac{\partial^2 \theta}{\partial t^2} =\; \nabla\left(\frac{1}{\chi}\frac{\partial m_z}{\partial t}\right) =\; \nabla \left(\frac{\rho_s}{\chi}\nabla^2 \theta\right)}
Removing all spatial derivative operator from the l.h.s and r.h.s, we get:
Which is a wave equation whose frequency is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{\vec{k}} = \pm \sqrt{\frac{\rho_s}{\chi}}|\vec{k}|}
So, we have a new mode which exists in the ordered phase (below a certain critical temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c \,} ) which is a SPIN WAVE.
Now, let's consider the situation with dissipation.
Constitutive relations can be written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle j_{Q_\mu}=-K_{\mu \nu}\nabla _\nu T} (here we have direction dependence since we are working with ordered phase of planar ferromagnet)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle (j_{m_z}+h_\theta)_\mu = - \Gamma _{\mu \nu}\nabla _\nu h}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle X'=\gamma \nabla h_\theta = \gamma \rho_s \nabla ^2 \theta} (here we are working with a scalar quantity, no direction dependence)
Linearing about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle m_z = 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \nabla \theta = 0} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle h = 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle h_\theta = 0} on average, respectively
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \nabla j_Q \approx \nabla j_\epsilon = -\frac {\partial \epsilon}{\partial t} = -K_{\mu \nu} \nabla _\mu \nabla _\nu T}
Combining with the following thermodynamic relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle d \epsilon = CdT}
we obtain the equation of motion for the energy which is a diffusive mode
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \frac {\partial \epsilon}{\partial t} = \frac {K_ {\mu \nu}}{C} \nabla _\mu \nabla _\nu \epsilon}
Now let's solve for the equation for the spin wave excitation from the system of equations that coupled the fluctuations of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle m_z} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \theta} . We have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \frac {\partial m_z}{\partial t} = - \nabla j_{m_z} = \nabla (h_\theta)+ \nabla _\mu \Gamma _{\mu \nu} \nabla _\nu h}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \frac {\partial v_\theta}{\partial t} = \nabla h + \nabla X'}
It follows that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \frac {\partial m_z}{\partial t} = \rho_s \nabla ^2 \theta + \frac {\Gamma _{\mu \nu}}{\chi} \nabla _\mu \nabla _\nu m_z}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \frac {\partial \theta}{\partial t} = \frac {m_z}{\chi} + \gamma \rho _s \nabla ^2 \theta}
One way to solve this coupled system is to go to Fourer space
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle m_z(\bold r , t) = \int_{- \infty}^{+ \infty} {\frac {d \omega}{2 \pi}\sum_{\bold k} e^{i \bold k \bold r}e^{-i \omega t} m_z(\bold k , \omega)}}
and similarly for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \theta }
We derive to the following system of equations in Fourier space
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -i \omega \left( \begin{array}{c} {m_z (\bold k , \omega)} \\ {\theta (\bold k , \omega)} \end{array} \right) = \left( \begin{array}{cc} {\frac {\Gamma _{\mu \nu}}{\chi}k _\mu k _\nu} & {-\rho_ s k^2} \\ {\frac 1 {\chi}} & {- \gamma \rho_ s k^2} \end{array} \right) \left( \begin{array}{c} {m_z (\bold k , \omega)} \\ {\theta (\bold k , \omega)} \end{array} \right)}
This system can be decoupled by diagonalizing the 2 by 2 matrix. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \lambda } be the eigenvalue of the matrix, we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \left( - \frac {\Gamma _{\mu \nu}}{\chi} k_\mu k_\nu - \lambda \right) \left( - \gamma \rho _s k^2 - \lambda \right) + \frac 1 {\chi} \rho _s k^2 =0}
This quadratic equation can be solved easily, yielding
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle -i \omega = \lambda = -\frac 1 {2 \chi} \Gamma _{\mu \nu} k_ \mu k_ \nu - \frac {1} {2} \gamma \rho_ s k^2 \pm \sqrt {\frac {1}{4}(\frac 1 {\chi} \Gamma _{\mu \nu} k_ \mu k_ \nu + \gamma \rho_ s k^2)^2 - \frac {\rho_ s}{\chi}k^2 - \frac {\gamma \rho_s}{\chi}k^2 k_ \mu k_ \nu \Gamma_ {\mu \nu}} }
At small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \bold k} we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \omega \approx \mp \sqrt {\frac {\rho_ s}{\chi}}k - i \left( \frac 1 {2} \gamma \rho_ s k^2 + \frac 1 {2 \chi} \Gamma_ {\mu \nu} k_ \mu k_ \nu\right) + O(k^3)}
So in the present of dissipation we obtain a damping spin wave. The osillating frequency is characteried by the real part of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \omega } which is linear in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle k } . Whereas, there damping frequency is characterized by the imaginary part of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \omega } which is proporotioanl to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle k^2 } .
In conclusion, at high temperature, there are two diffusive modes associated with two conserved quantities (energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \epsilon } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle z } component of the total magnetization). At low temperature, the system is characterized by energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \epsilon } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle m_z } and broken symmetry variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \nabla \theta } . In this case, the equation of motion for the energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \epsilon } is uncoupled and is still diffusive. On the other hand, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle m_z } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \nabla \theta } are coupled to each other, resulting in two damping wave modes for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle m_z } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \nabla \theta } .
Summary
In the previous section, we have just studied the hydrodynamics of a simple model of planar ferromagnet. Many concepts and results are quite general for the hydrodynamics of all systems. The most important of these are listed below:
- Long wavelengh, low frequency excitations are related to conservation laws and broken symmetry.
- There is exactly one mode associated with each conservation law and each broken symmetry.
- Currents of hydrodynamic variables contain reactive and dissipative parts.
- In the absence of reactive couplings, the hydrodynamic modes are diffusive.
- Diffusion constants are the ratio of a transport coefficient to a susceptibility.
- The velocity of propagating modes are square roots of the ratio of a reactive transport
- and a susceptibility.
- Dissipative coefficients are related to current correlation function via Kubo Formula.
- Elementary excitations from the ground state can be described by a harmonic Hamiltonian.
- There must be a zero-frequency, zero wave number mode in systems with a continuous broke symmetry.
Adiabatic principle
When entering research people usually find that the most difficult question is where to start, especially when confronted with something that is actually new.
The adiabatic continuity principle tells us to search for the right simple problem when confronted with a complicated one. As long as the simple problem describes a correct physical state of matter, and so we do not risk crossing a phase boundary, we can start with some non-interacting model system as an unperturbed Hamiltonian and calculate the properties of the system in question by perturbation theory.
One thing we can not do is to continue past a symmetry boundary: the very obvious failure of analyticity of free energy at such boundary shows that this can not be done. It is also clear that two states of different symmetry can not be reached by simple continuation from the same state.
Theoretical methods
"Second" quantization
For many body system, an convenient formalism is developed. Defining operators which create or annihilate particles in specified states allows for much simpler bookkeeping, and more transparent physical interpretation, than the use of Slater determinants. Operators of physical interest may be expressed in terms of these creation and annihilation operators. It is noteworthy, and quite useful, that the eigenstates of annihilation operators are coherent states, a natural representation - the holomorphic representation.
Quantum Mechanics of a single particle
The state of a particle is described by a state vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\phi \rangle} , which belongs to a Hilbert space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} . Using Dirac notation, the scalar product of vectors in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\phi|\psi\rangle=\int d^3r\phi^*(\vec{r})\psi(\vec{r})}
Particularly, eigenvectors of the quantum position operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\vec{r}}} and momentum operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{ \vec{p}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\vec{r}}|\vec{r}\rangle=\vec{r}|\vec{r}\rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\vec{p}}|\vec{p}\rangle=\vec{p}|\vec{p}\rangle}
A state vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{r}\rangle} represents a state in which the particle is localized at point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}} , and a state vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{p}\rangle} represents a particle with a momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}} . The overlap of these vectors is given by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \vec{r}|\vec{r}^'\rangle=\delta^{(3)}(\vec{r}-\vec{r}^')}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \vec{p}|\vec{p}^'\rangle=\delta^{(3)}(\vec{p}-\vec{p}^')}
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\vec{r}|\vec{p}\rangle=(\frac{1}{2\pi\hbar})^{\frac{3}{2}}\exp{\frac{i\vec{p}\cdot\vec{r}}{\hbar}}}
System of Identical Particles
The Hilbert space of states for a system of N identical particles is the space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N} of complex, square integrable functions, defined in the configuration space of the N paticles. The wave function is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_N(\vec{r}_1,\vec{r}_2, ..., \vec{r}_N)} , which represents the probability amplitude for finding particles at the N positions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}_1,\vec{r}_2, ..., \vec{r}_N} .
As we have defined it, the Hilbert, space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N} is simply the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N^{th}} tensor product of the single-particle Hilbert space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N=H\otimes H \otimes ... \otimes H}
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {|\alpha\rangle} } is an orthonormal basis of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} the canonical orthonormal basis of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N} is constructed from the tensor products:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha_1 ... \alpha_N ) \equiv |\alpha_1\rangle \otimes |\alpha_2 \rangle \otimes ... \otimes |\alpha_N\rangle }
Note for future reference that the states defined in this way utilize a curved bracket in the ket symbol. These basis states have the wave functions:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{\vec{\alpha}_1, \vec{\alpha}_2, ... , \vec{\alpha}_N}(\vec{r}_1,...,\vec{r}_N)=(\vec{r}_1...\vec{r}_N|\alpha_1...\alpha_N)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad =(\langle \vec{r}_1|\otimes \langle \vec{r}_2 |\otimes ... \otimes \langle \vec{r}_N|)(|\alpha_1 \rangle \otimes | \alpha_2\rangle\otimes ... \otimes | \alpha_N\rangle)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \qquad =\phi_{\alpha_1}(\vec{r}_1)\phi_{\alpha_2}(\vec{r}_2)...\phi_{\alpha_N}(\vec{r}_N)}
The overlap of two vectors of the basis is given by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\alpha_1 \alpha_2... \alpha_N |\alpha^'_1 \alpha^'_2 ... \alpha^'_N )=(\langle \alpha_1|\otimes\langle \alpha_2| \otimes ...\otimes \langle \alpha_N|)(|\alpha^'_1\rangle\otimes |\alpha^'_2\rangle \otimes ... \otimes | \alpha^'_N\rangle)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\langle\alpha_1|\alpha^'_1\rangle \langle \alpha_2|\alpha^'_2\rangle ...\langle \alpha_N|\alpha^'_N\rangle }
and the completeness of the basis is obtained from the tensor product of the completeness relation far the basis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {|\alpha\rangle}} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\alpha_1,\alpha_2,...,\alpha_N}|\alpha_1\alpha_2...\alpha_N)(\alpha_1\alpha_2...\alpha_N|=1}
where 1 now represents the unit operator in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N} . Physjcally, it is clear that the space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N} is generated by linear combinations of products of single-particle wave functions. Thus far, in defining the Hilbert space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N} , we have not taken into account the symmetry property of the wave function. In contrast to the multitude of pure and mixed symmetry states one could define mathematically, only totally symmetric and antisymmetric states are observed in nature, Particles occurring in symmetric or antisymmetric states are called Bosons and Fermions respectively.
The wave function of N Bosons is totally symmetric and thus satisfies
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\vec{r}_{P_1}, \vec{r}_{P_2}, ..., \vec{r}_{P_N} )=\psi(\vec{r}_1,\vec{r}_2,...,\vec{r}_N)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (P_1,P_2,...,P_N)} represents any permutation P of the set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,2,...,N)} .
The wave function of N Fermions is antisymmetric under the exchange of any pair of particles and therefore satisfies:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\vec{r}_{P_1}, \vec{r}_{P_2}, ..., \vec{r}_{P_N} )=(-1)^P\psi(\vec{r}_1,\vec{r}_2,...,\vec{r}_N)}
Here, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1)^P} denotes the sign, or parity, of the permutation P, and is defined as the parity of the number of transpositions of two elements which brings the permutation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (P_1, P_2,... , P_N)} to its original form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,2,..., N)} .
Although the symmetry requirements for Bosons and Fermions are ultimately founded on experiment. It may be proven within the context of quantum field theory that given general assumptions of locality, causality and Lorentz invariance. Particles with integer spin (O,1,2, ...) are Bosons and particles with half-integer spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{2},\frac{3}{2},...\right)} are Fermions. Familiar samples of Bosons include photons, pions, mesons, gluons,and the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^4He} atom. Examples of Fermions include protons, neutrons, electrons, muons, neutrinos, quarks, and the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^3He} atom. Composite particles composed of any number of Bosons and an even or odd number of Fermions behave as Bosons or Fermions respectively at energies sufficiently low compared to their binding energy.
For convenience, we shall adopt the following unified notation for Bosons or Fermions:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\vec{r}_{P_1}, \vec{r}_{P_2}, ..., \vec{r}_{P_N} )=(\zeta)^P\psi(\vec{r}_1,\vec{r}_2,...,\vec{r}_N)}
where P is the parity of the permutation, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta} is +1 or -1 for Bosons or Fermions respectively.
These symmetry requirements imply corresponding restrictions of the Hilbert space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N} of N-particle systems. A wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\vec{r}_1,\vec{r}_2,...,\vec{r}_N)} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N} belongs to the Hilbert space of N Bosons, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_N} , or the Hilbert space of N Fermions, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_N} . If it is symmetric or antisymmetric respectively, under a permutation of the particles.
We will define the symmetrization operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_B} and the antisymmetrization operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_F} in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N} by their action on a wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\vec{r}_1,\vec{r}_2,...,\vec{r}_N)} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{{^B_F}}\psi(\vec{r}_1,...,\vec{r}_N)=\frac{1}{N!}\sum_P\zeta^P\psi(\vec{r}_{P_1},\vec{r}_{P_2},...,\vec{r}_{P_N})}
The manifestly Hermitian operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{^B_F}} may be shown to be a projector as follows.
For any wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P^2_{{^B_F}}\psi(\vec{r}_1,...,\vec{r}_N)=\frac{1}{N!}\frac{1}{N!}\sum_P\sum_{P'}\zeta^{P'}\zeta^P\psi(\vec{r}_{{P'}_1P_1},\vec{r}_{{P'}_2P_2},...,\vec{r}_{{P'}_NP_N})}
where P'P denotes the group composition of P' and P. Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta^{P+P'}=\zeta^{P'P}} , the summation over P and P' can be replaced by a summation over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q=P'P} and P:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P^2_{{^B_F}}\psi(\vec{r}_1,...,\vec{r}_N)=\frac{1}{N!}\sum_P(\frac{1}{N!}\sum_Q\zeta^{Q}\psi(\vec{r}_{Q_1},...,\vec{r}_{Q_N}))}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{1}{N!}\sum_PP_{^B_F}\psi(\vec{r}_1,..., \vec{r}_N)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =P_{^B_F}\psi(\vec{r}_1,..., \vec{r}_N)}
Using these project8cs, a system of Bosons or Fermions, with one particle in state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1} , one particle in state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_2} , . . ., and oone particle in state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_N} , are represented as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha_1 ... \alpha_N\} \equiv \sqrt{N!}P_{\{^B_F\}}|\alpha_1...\alpha_N)} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{1}{\sqrt{N!}}\sum_P\zeta^P|\alpha_{P_1}\rangle\otimes |\alpha_{P_2}\rangle \otimes ...\otimes |\alpha_{P_N}}
The scalar product of two such vectors constructed from the same basis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha\rangle} is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\alpha'_1 ... \alpha'_N|\alpha_1 ...\alpha_N\}=N!(\alpha'_1...\alpha'_N|P^2_{^B_F}|\alpha_1...\alpha_N) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =N!(\alpha'_1...\alpha'_N|P_{^B_F}|\alpha_1...\alpha_N)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sum_P \zeta^P\langle \alpha'_1|\alpha_{P_1}\rangle...\langle \alpha'_N|\alpha_{P_N}\rangle}
Because of the orthogonality of the basis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha\rangle} , the only non-vanishing terms in the right hand side of equation above are the permutations P such that:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha'_1=\alpha_{P_1},\alpha'_2=\alpha_{P_2}, ..., \alpha'_N=\alpha_{P_N}}
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha'_1, . . . , \alpha'_N} is a permutation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1, . . . , \alpha_N} , the overlap may be evaluated straightfowardly. For Fermions. since there is at most one particle per state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha\rangle} , no two identical states can be present in the set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ \alpha_1,...,\alpha_N\}} and therefore, there exists only one permutation P which transforms Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1,...,\alpha_N} into Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha'_1,...,\alpha'_N} . The sum thus reduces to one term, and if the states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha_i\rangle} are normalized, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\alpha'_1 ... \alpha'_N|\alpha_1 ...\alpha_N\}=(-1)^P} ( Fermions ) .
For Bosons, many particles may be in the same state, and therefore, any permutation which does interchange particles in the same state contributes to the sum. The overlap is thus equal to the total number of permutations which transform Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1,...,\alpha_N} into Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha'_1,...,\alpha'_N} . If the set of states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1,...,\alpha_N} represents a system with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_1} Bosons in state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_2} Bosons in state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_2} , . . . , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_p} Bosons in state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_p} , where the states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1,...,\alpha_p} are distinct, the overlap is given by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\alpha'_1 ... \alpha'_N|\alpha_1 ...\alpha_N\}=n)_1!n_2!...n_p!} ( Bosons ) .
Combining Fermions and Bosons together:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\alpha'_1 ... \alpha'_N|\alpha_1 ...\alpha_N\}=\zeta^P\prod_\alpha n_\alpha!}
Thus, the orthonormal basis for Fermions and Bosons are:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha_1...\alpha_N\rangle=\frac{1}{\sqrt{\prod_\alpha n_\alpha!}}|\alpha_1...\alpha_N\}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{1}{\sqrt{N!\prod_\alpha n_\alpha!}}\sum_P\zeta^P|\alpha_{P_1}\rangle \otimes|\alpha_{P_2}\rangle \otimes ...\otimes |\alpha_{P_N}\rangle}
Many-body Operators
We now consider matrix elements of many-body operators in the canonical basis of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_N} . From these, the representation of operators in the spaces Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_N} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_N} follows straightforwardly using the symmetrization and antisymmetrization operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{^B_F}} .
let O be an arbitrary operator In Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_N} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_N} . Independent of whether the particles are Bosons or Fermions, their indistinguishability implies that O is invariant under any permutation of the particles. Thus, for any states, and any permutation P:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\beta_{P_1}...\beta_{P_N}|O|\beta'_{P_1}...\beta'_{P_N})=(\beta_{1}...\beta_{N}|O|\beta'_{1}...\beta'_{N})}
We begin by considering the care of one-body operators. An operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}} is a one-body operator if the action of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}} on a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha_1...\alpha_N\rangle} of N particles is the sum of the action of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}} on each particle:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}|\alpha_1...\alpha_N)=\sum^N_{i=1}\hat{U}_i|\alpha_1...\alpha_N)}
where the operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}_i} operates only on the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{th}} particle.
The matrix element of a one-body operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{U}_i} between two states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha_1...\alpha_N)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\beta_1...\beta_N)} is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\alpha_1...\alpha_N|\hat{U}|\beta_1...\beta_N)=\sum^N_{i=1}(\alpha_1...\alpha_N|\hat{U}_i|\beta_1...\beta_N)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sum^N_{i=1}\prod_{k\neq i}\langle \alpha_k|\beta_k\rangle \cdot \langle\alpha_i|\hat{U}|\beta_i\rangle}
Similarly, two-body operators may be expressed in terms of creation and annihilation operators. Two-body operators, i.e. operators which engage two-particles
E.g. symmetric pairwise interaction: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x,x^{'})\equiv V(x^{'},x)}
(such as Coulomb) acting between two-particle states
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{V}=\frac{1}{2}\int dx\int dx^{'}\mid x,x^{'}>V(x,x^{'})<x,x^{'}\mid}
When acting on many-particle states,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{V}\mid x_{1},x_{2},...x_{N}>=\frac{1}{2}\sum_{n\neq m}^{N}V(x_{n},x_{m})\mid x_{1},x_{2},...x_{N}>}
How can one express ˆ V in second quantised form? We might guess that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{V}=\frac{1}{2}\int dx\int dx^{'}a^{+}(x)a^{+}(x^{'})V(x,x^{'})a(x^{'})a(x)}
i.e. annihilation operators check for presence of particles at x and x’ — if they exist, asign the potential energy and then recreate particles in correct order (viz. statistics). we use factor of two for double-counting.
check:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^{+}(x)a^{+}(x^{'})V(x,x^{'})a(x^{'})a(x)\mid x_{1},x_{2},...x_{N}>=a^{+}(x_{1})a^{+}(x_{2})...a^{+}(x_{N})\mid\Omega>} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid\Omega>} is the vaccum state.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=1}^{N}\zeta^{n-1}\delta(x-x_{n})a^{+}(x_{n})a^{+}(x^{'})a(x^{'})a^{+}(x_{1})...a^{+}(x_{n-1})a^{+}(x_{n+1})...a^{+}(x_{N})\mid\Omega>}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=1}^{N}\zeta^{n-1}\delta(x-x_{n})\sum_{m(\neq n)}^{N}\delta(x^{'}-x_{m})a^{+}(x_{n})a^{+}(x_{1})...a^{+}(x_{n-1})a^{+}(x_{n+1})...a^{+}(x_{N})\mid\Omega>} where we used Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^{+}(x^{'})a(x^{'})=n(x^{'}).}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sum_{n,m(\neq n)}^{N}\delta(x-x_{n})\delta(x^{'}-x_{m})\mid x_{1},x_{2},...x_{N}>}
then multiplying by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x,x^{'})/2} , and integrate over x and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{'}} we get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{V}} .
In general, we define an n-body operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{R}} as an operator which acts on a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\alpha_1...\alpha_N\rangle} in the following way:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{R}|\alpha_1...\alpha_N)=\frac{1}{n!}\sum_{1\leq i_1\neq i_2\neq...\neq i_n \leq N}\hat{R}_{i_1i_2...i_n}|\alpha_1...\alpha_N)}
That is, the action of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{R}} on a state of N particles is the sum of the action of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{R}} on all distinct subsets of n-particles. Analogous to the previous cases, the matrix elements of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{R}} satisfy:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{(\alpha_1...\alpha_N|\hat{R}|\beta_1...\beta_N)}{(\alpha_1...\alpha_N|\beta_1...\beta_N)}=\frac{1}{n!}\sum_{i_1\neq i_2 \neq ...\neq i_n}\frac{(\alpha_{i_1}...\alpha_{i_n}|\hat{R}|\beta_{i_1}...\beta_{i_n})}{\langle\alpha_{i_1}|\beta_{i_1}\rangle\langle\alpha_{i_2}|\beta_{i_2}\rangle ... \langle \alpha_{i_n}|\beta_{i_n}\rangle}}
and an n-body operator is entirely determined by its matrix elements Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\alpha_1...\alpha_n|\hat{R}|\beta_1...\beta_n)} in the Hilbert space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_n} of n-particle systems.
Creation and Annihilation Operators
Creation and annihilation operators provide a convenient representation of the many-particle states and many-body operators introduced in the preceding sections. These operators generate the entire Hilbert space by their action on a single reference state and provide a basis for the algebra of operators of the Hilbert space.
For each single-particle state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\lambda\rangle} of the single-particle space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} , we define a Boson or Fermion creation operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^{\dagger}_\lambda} by its action on any symmetrized or antisymmetrized state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\lambda_1 ... \lambda_N \}} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_N} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_N} as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^{\dagger}_\lambda|\lambda_1... \lambda_N\}\equiv |\lambda |\lambda_1...\lambda_N \}}
For the present treatment, it is convenient to use an orthonormal basis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ |\lambda_i\}} , for which the definition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^\dagger_\lambda} may also be written
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^\dagger_\lambda|\lambda_1...\lambda_N\rangle=\sqrt{n_\lambda+1}|\lambda\lambda_1...\lambda_N\rangle}
Any basis vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\lambda_1...\lambda_N\}} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\lambda_1...\lambda_N\rangle} may be generated by repeated action of the creation operators on the vacuum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0\rangle} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\lambda_1...\lambda_N\}=a^\dagger_{\lambda_1}a^\dagger_{\lambda_2}...a^\dagger_{\lambda_N}|0\rangle}
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\lambda_1...\lambda_N\}=\frac{1}{\sqrt{\prod_\lambda n_\lambda!}}a^\dagger_{\lambda_1}a^\dagger_{\lambda_2}...a^\dagger_{\lambda_N}|0\rangle}
Thus, the creation operators generate the entire Fock space by repeated action on the vacuum.
Bosons satisfy the commutation relations
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a_\lambda, a^\dagger_\mu]_-=\delta_{\lambda\mu} (Bosons)}
Fermions satisfy the anticommutation relations
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a_\lambda, a^\dagger_\mu]_+=\delta_{\lambda\mu} (Fermions)}
A particularly useful equation for creation and annihilation operators is knowing how to switch them from one basis to another. This equation can be written as: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^\dagger_\mu = \sum_\lambda <\lambda | \mu> a^\dagger_\lambda }
Using this equation we can define field operators, traditionally denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\psi}^\dagger(x)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\psi}(x)} , which are creation and annihilation operators in position basis, which are particularly useful.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\psi}^\dagger(x) = \sum_\mu <\mu| x> a^\dagger_\mu = \sum_\mu \phi^*_\mu(x)a^\dagger_\mu } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\psi}(x) = \sum_\mu <\mu|x> a_\mu = \sum_\mu\phi_\mu(x)a_\mu }
Their commutation relations are: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\hat{\psi}^\dagger(x),\hat{\psi}^\dagger(y)]_{-\zeta}=[\hat{\psi}(x),\hat{\psi}(y)]_{-\zeta}=0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\hat{\psi},\hat{\psi}^\dagger(y)]_{-\zeta}=\delta(x-y)}
Functional path integrals
The concept of path integration will be extended from quantum mechanics to quantum field theory.
The basic idea of the many-body path integral is to segment the time evolution of a quantum(many-body) Hamiltonian into infinitesimal time slices and to absorb as much as possible of the quantum dynamical phase accumulated during the short-time propagation into a set of suitably chosen eigenstates.In the context of single-particle quantum mechanics, the Hamiltonian is presented by coordinate and momentum eigenstates. Given that many-body Hamiltonian is conveniently expressed in terms of creation/ annihilation operators, an obvious idea would be to search for eigenstates of these operators. Such states are called coherent states.
Boson coherent states
In this section, a very important and useful basis of the Fock space is introduced. It is called coherent states basis, and the states are defined as eigenstates of the annihilation operators.
From a historical point of view this was the first example of quantum dynamics when Erwin Schrödinger derived it in 1926 while searching for solutions of the Schrödinger equation that satisfy the correspondence principle. Nowadays the coherent state mechanism is heavily used in Solid State Physics and beyond. One of their distinct features is overcompleteness.
This field broadened itself so much that encapsulated areas like applied mathematics and mathematical physics in general, with many applications. To distinct the coherent states associated to the quantum harmonic oscillator we usually call them canonical coherent states (CCS) or standard coherent states or Gaussian states.
Someone may find applications of the coherent states formalism in: signal and image processing, Quantum optics, treatment of general potentials in quantum mechanics, quantum non perturbing measurements, Bose–Einstein condensates, superconductivity and superfluidity, Klein-Gordon and Dirac equations, even in String theory and loop quantum gravity, in our attempts to unify the fundamental forces of nature.
Definition
Assuming a state in Fock space, there must be substantial components with different particle numbers. There exists a component which has the minimum number of particles. The creation operator defines the coherent state. This component will disappear after the creation operator operates on it, so that it is not the original state anymore. As a result, eigenstates for creation operators are not well defined. Hence, to define coherent states, annihilation operators are chosen.
In the case of one particle, assume that annihilation operators' eigenstate is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vert\phi\rangle} with eigenvalue Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vert\phi\rangle =c_{0}|0\rangle + c_{1}a^{+}|0\rangle+ c_{2}(a^{+})^{2}|0\rangle + \dotsb = \sum\limits_{j=0}^{\infty} c_{j}\frac{1}{\sqrt{j!}}(a^{+})^{j}|0\rangle}
So that,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\vert\phi\rangle= \sum\limits_{j=0}^{\infty} c_{j}\frac{1}{\sqrt{j!}}a(a^{+})^{j}|0\rangle= \sum\limits_{j=0}^{\infty} c_{j}\frac{1}{\sqrt{j!}}j(a^{+})^{j-1}|0\rangle= \sum\limits_{j=1}^{\infty} c_{j}\frac{\sqrt{j}}{\sqrt{(j-1)!}}(a^{+})^{j-1}|0\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sum\limits_{j^{\prime}=0}^{\infty} c_{j^{\prime}+1}\frac{\sqrt{j^{\prime}+1}}{\sqrt{j^{\prime}!}}(a^{+})^{j^{\prime}}|0\rangle= \sum\limits_{j=0}^{\infty} c_{j+1}\frac{\sqrt{j+1}}{\sqrt{j!}}(a^{+})^{j}|0\rangle= \phi\sum\limits_{j=0}^{\infty} c_{j}\frac{1}{\sqrt{j!}}(a^{+})^{j}|0\rangle}
Here we have used Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a,a^{+}]=1} , and we can conclude that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{j+1}\sqrt{j+1}=c_{j}\phi} .
Assume that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{j}=\frac{\phi^{j}}{\sqrt{j!}}} , which satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{j+1}c_{j+1}=\frac{\phi^{j+1}}{\sqrt{(j+1)!}}\sqrt{j+1}= \frac{\phi\cdot\phi^{j}}{\sqrt{j!}}= \phi\cdot c_{j}}
So Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vert\phi\rangle= \sum\limits_{j=0}^{\infty}\frac{1}{j!} (\phi a^{+})^{j}\vert 0\rangle=e^{\phi a^{+}}\vert 0\rangle}
For many-particle coherent state, we need Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}\vert\phi\rangle=\phi_{\alpha}\vert\phi\rangle}
Hence, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vert\phi\rangle= \prod\limits_{\alpha} e^{\phi_{\alpha} a_{\alpha}^{+}}|0\rangle= e^{\sum_{\alpha}\phi_{\alpha} a_{\alpha}^{+}}|0\rangle} .
Expand a boson coherent state in the occupation number representation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\phi\right\rangle =\underset{n_{\alpha_{1}},n_{\alpha_{2}}\cdots n_{\alpha_{p}}}{\sum}\phi_{n_{\alpha_{1}},n_{\alpha_{2}}\cdots n_{\alpha_{p}}}\left|n_{\alpha_{1}},n_{\alpha_{2}}\cdots n_{\alpha_{p}}\cdots\right\rangle } ,
Set the eigenequation: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha i}\left|\phi\right\rangle =\phi_{\alpha i}\left|\phi\right\rangle } .
Compare the above two equations, we get:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\alpha i}\phi_{n_{\alpha_{1}},n_{\alpha_{2}}\cdots(n_{\alpha_{i}-1})\cdots}=\sqrt{n_{\alpha i}}\phi_{n_{\alpha_{1}},n_{\alpha_{2}}\cdots n_{\alpha_{i}}\cdots}}
To satisfy this relation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{n_{\alpha_{1}},n_{\alpha_{2}}\cdots n_{\alpha_{i}}\cdots}=\frac{\phi_{\alpha_{1}}^{n_{\alpha_{1}}}\phi_{\alpha_{2}}^{n_{\alpha_{2}}}\cdots\phi_{\alpha i}^{n_{\alpha i}}\cdots}{\sqrt{n_{\alpha_{1}}!}\sqrt{n_{\alpha_{2}}!}\cdots\sqrt{n_{\alpha i}!}\cdots}.}
Recall Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|n_{\alpha_{1}},n_{\alpha_{2}}\cdots n_{\alpha_{i}}\cdots\right\rangle =\frac{(a_{\alpha_{1}}^{_{\dagger}})^{n_{\alpha_{1}}}}{\sqrt{n_{\alpha_{1}}!}}\frac{(a_{\alpha_{2}}^{_{\dagger}})^{n_{\alpha_{2}}}}{\sqrt{n_{\alpha_{2}}!}}\cdots\frac{(a_{\alpha_{p}}^{_{\dagger}})^{n_{\alpha_{p}}}}{\sqrt{n_{\alpha_{p}}!}}\cdots\left|0\right\rangle } ,
So we obtain:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\phi\right\rangle =\underset{n_{\alpha_{1}},n_{\alpha_{2}}\cdots n_{\alpha_{p}}}{\sum}\frac{(\phi_{\alpha_{1}}a_{\alpha_{1}}^{_{\dagger}})^{n_{\alpha_{1}}}}{n_{\alpha_{1}}!}\frac{(\phi_{\alpha_{2}}a_{\alpha_{2}}^{_{\dagger}})^{n_{\alpha2}}}{n_{\alpha_{2}}!}\cdots\frac{(\phi_{\alpha_{p}}a_{\alpha_{p}}^{_{\dagger}})^{n_{\alpha_{p}}}}{n_{\alpha_{p}}!}\left|0\right\rangle } .
Simplify it: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\phi\right\rangle =e^{\underset{\alpha}{\sum}\phi_{\alpha}a_{\alpha}^{_{\dagger}}}\left|0\right\rangle } , which is a standard form of boson coherent state.
Also: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi\right|=\left\langle 0\right|e^{\underset{\alpha}{\sum}\phi_{\alpha}^{*}a_{\alpha}}.}
Consider Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}^{_{\dagger}}\left|\phi\right\rangle} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}^{_{\dagger}}\left|\phi\right\rangle =a_{\alpha}^{_{\dagger}}e^{\underset{\alpha'}{\sum}\phi_{\alpha'}a_{\alpha'}^{_{\dagger}}}\left|0\right\rangle =\frac{\partial}{\partial\phi_{\alpha}}e^{\underset{\alpha'}{\sum}\phi_{\alpha'}a_{\alpha'}^{_{\dagger}}}\left|0\right\rangle =\frac{\partial}{\partial\phi_{\alpha}}\left|\phi\right\rangle .} .
or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}^{_{\dagger}}\left|\phi\right\rangle\prod\limits_{\alpha^{\prime}\neq\alpha} e^{\phi_{\alpha^{\prime}} a_{\alpha^{\prime}}^{+}} a_{\alpha}^{+} e^{\phi_{\alpha} a_{\alpha}^{+}}|0\rangle =\prod\limits_{\alpha^{\prime}\neq\alpha} e^{\phi_{\alpha^{\prime}} a_{\alpha^{\prime}}^{+}} a_{\alpha}^{+} ( 1+ \phi_{\alpha} a_{\alpha}^{+}+\frac{1}{2}\phi_{\alpha}^{2} a_{\alpha}^{+2}+\dotsb )|0\rangle =\prod\limits_{\alpha^{\prime}\neq\alpha} e^{\phi_{\alpha^{\prime}} a_{\alpha^{\prime}}^{+}} ( a_{\alpha}^{+}+ \phi_{\alpha} a_{\alpha}^{+2}+\frac{1}{2}\phi_{\alpha}^{2} a_{\alpha}^{+3}+\dotsb )|0\rangle =\frac{\partial}{\partial\phi_{\alpha}}\left|\phi\right\rangle}
Also: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi\right|a_{\alpha}=\frac{\partial}{\partial\phi_{\alpha}^{*}}\left\langle \phi\right|}
.
Let us consider the overlap Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi|\phi'\right\rangle } :
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{a}} is not Hermitian operator, its eigenstates are not orthogonal.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi|\phi'\right\rangle =\left\langle 0\right|e^{\underset{\alpha}{\sum}\phi_{\alpha}^{*}a_{\alpha}}e^{\underset{\alpha}{\sum}\phi_{\alpha}a_{\alpha}^{_{\dagger}}}\left|0\right\rangle .}
Using Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{A}e^{B}=e^{B}e^{A}e^{[A,B]}} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi|\phi'\right\rangle =\left\langle 0\right|e^{\underset{\beta}{\sum}\phi_{\beta}a_{\beta}^{_{\dagger}}}e^{\underset{\alpha}{\sum}\phi_{\alpha}^{*}a_{\alpha}}\left|0\right\rangle e^{\underset{\alpha,\beta}{\sum}\phi_{\alpha}^{*}\phi'_{\beta}\delta_{\alpha\beta}}=e^{\underset{\alpha}{\sum}\phi_{\alpha}^{*}\phi'_{\alpha}}} .
More details about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi|\phi'\right\rangle} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi|\phi'\right\rangle= \langle 0\vert ( e^{\phi_{0}^{*} a_{0}} e^{\phi_{0}^{\prime} a_{0}^{+}} ) ( e^{\phi_{1^{*}} a_{1}} e^{\phi_{1}^{\prime} a_{1}^{+}}) \dotsb e^{\phi_{n}^{*} a_{n}} e^{\phi_{n}^{\prime} a_{n}^{+}}|0\rangle} ,
1,2Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dotsb}
n denotes the nth particle.
as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\phi_{j}^{*}a_{j}}e^{\phi_{j}^{\prime}a_{j}^{+}}= e^{\phi_{j}^{*} a_{j}+\phi_{j}^{\prime}a_{j}^{+}+\frac{1}{2}[\phi_{j}^{*}a_{j},\phi_{j}^{\prime}a_{j}^{+}]}= e^{\phi_{j}^{*}a_{j}+\phi_{j}^{\prime} a_{j}^{+}+\frac{1}{2}\phi_{j}^{*}\phi_{j}^{\prime}}}
similarly,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle $e^{\phi_{j}^{\prime}a_{j}}e^{\phi_{j}^{*}a_{j}^{+}}= e^{\phi_{j}^{\prime} a_{j}+\phi_{j}^{*}a_{j}^{+}+\frac{1}{2}[\phi_{j}^{\prime} a_{j},\phi_{j}^{*}a_{j}^{+}]} = e^{\phi_{j}^{\prime}a_{j}+\phi_{j}^{*}a_{j}^{+}+\frac{1}{2}\phi_{j}^{\prime}\phi_{j}^{*}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\phi_{j}^{*}a_{j}}e^{\phi_{j}^{\prime}a_{j}^{+}}e^{-\frac{1}{2}\phi_{j}^{*}\phi_{j}^{\prime}}= e^{\phi_{j}^{\prime}a_{j}}e^{\phi_{j}^{*}a_{j}^{+}}e^{\frac{1}{2}\phi_{j}^{\prime}\phi_{j}^{*}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\phi_{j}^{*} a_{j}} e^{\phi_{j}^{\prime} a_{j}^{+}} = e^{\phi_{j}^{\prime} a_{j}} e^{\phi_{j}^{*} a_{j}^{+}}e^{\phi_{j}^{\prime} \phi_{j}^{*}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle 0\vert^{\phi_{j}^{*} a_{j}} e^{\phi_{j}^{\prime} a_{j}^{+}} |0\rangle=e^{\phi_{j}^{\prime} \phi_{j}^{*}}}
so,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi|\phi'\right\rangle=e^{\underset{\alpha}{\sum}\phi_{\alpha}^{*}\phi'_{\alpha}}}
A crucial property of the Bosonic coherent states is their overcompleteness in the Fock space.
The unit operator in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\phi\right\rangle } basis:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\underset{\alpha}{\prod}\frac{d\phi_{\alpha}^{*}d\phi_{\alpha}}{2\pi i}e^{-\underset{\alpha}{\sum}\phi_{\alpha}^{*}\phi{}_{\alpha}}\left|\phi\right\rangle \left\langle \phi\right|=1} .
Proof:
Using Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\phi_{\alpha}^{*}d\phi_{\alpha}}{2\pi i}=\frac{d(Re\phi_{\alpha})d(Im\phi_{\alpha})}{\pi}} ,
the method to prove the identity is to show that the l.h.s commutes with all creation and annihilation operators. Then it must be proportional to 1.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a_{\alpha,}\left|\phi\right\rangle \left\langle \phi\right|]=a_{\alpha}\left|\phi\right\rangle \left\langle \phi\right|-\left|\phi\right\rangle \left\langle \phi\right|a_{\alpha}=(\phi_{\alpha}-\frac{\partial}{\partial\phi_{\alpha}^{*}})\left|\phi\right\rangle \left\langle \phi\right|} ,
So, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a_{\alpha,}\int\underset{\alpha'}{\prod}\frac{d\phi_{\alpha'}^{*}d\phi_{\alpha'}}{2\pi i}e^{-\underset{\alpha'}{\sum}\phi_{\alpha'}^{*}\phi{}_{\alpha'}}\left|\phi\right\rangle \left\langle \phi\right|]=\int\underset{\alpha'}{\prod}\frac{d\phi_{\alpha'}^{*}d\phi_{\alpha'}}{2\pi i}e^{-\underset{\alpha'}{\sum}\phi_{\alpha'}^{*}\phi{}_{\alpha'}}(\phi_{\alpha}-\frac{\partial}{\partial\phi_{\alpha}^{*}})\left|\phi\right\rangle \left\langle \phi\right|=\int\underset{\alpha'}{\prod}\frac{d\phi_{\alpha'}^{*}d\phi_{\alpha'}}{2\pi i}(\phi_{\alpha}+\frac{\partial}{\partial\phi_{\alpha}^{*}})e^{-\underset{\alpha'}{\sum}\phi_{\alpha'}^{*}\phi{}_{\alpha'}}\left|\phi\right\rangle \left\langle \phi\right|=0} . (The last step is done through integration by parts. )
Similarly for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}^{\dagger}} .
So the l.h.s of the identity commutes with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}^{\dagger} } for any Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle 0\right|l.h.s\left|0\right\rangle =\int\underset{\alpha}{\prod}\frac{d\phi_{\alpha}^{*}d\phi_{\alpha}}{2\pi i}e^{-\underset{\alpha}{\sum}\phi_{\alpha}^{*}\phi{}_{\alpha}}\left\langle 0|\phi\right\rangle \left\langle \phi|0\right\rangle =\int\underset{\alpha}{\prod}\frac{d(Re\phi_{\alpha})d(Im\phi_{\alpha})}{\pi}e^{-\underset{\alpha}{\sum}[(Re\phi{}_{\alpha})^{2}+(Im\phi{}_{\alpha})^{2}]}=1} .
Thus, we have proven the validity of this form of the unity operator.
The trace of one operator:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle TrA=\int\underset{\alpha}{\prod}\frac{d\phi_{\alpha}^{*}d\phi_{\alpha}}{2\pi i}e^{-\underset{\alpha}{\sum}\phi_{\alpha}^{*}\phi{}_{\alpha}}\left\langle \phi\right|A\left|\phi\right\rangle } .
Proof:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle TrA= \sum\limits_{n}\langle n|A|n\rangle= \int\underset{\alpha}{\prod}\frac{d\phi_{\alpha}^{*}d\phi_{\alpha}}{2\pi i}e^{-\underset{\alpha}{\sum}\phi_{\alpha}^{*}\phi{}_{\alpha}} \sum\limits_{n}\langle n|\phi\rangle \langle \phi|A|n \rangle= \int\underset{\alpha}{\prod}\frac{d\phi_{\alpha}^{*}d\phi_{\alpha}}{2\pi i}e^{-\underset{\alpha}{\sum}\phi_{\alpha}^{*}\phi{}_{\alpha}} \sum\limits_{n} \langle \phi|A|n \rangle \langle n|\phi\rangle }
as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi|\phi'\right\rangle=e^{\underset{\alpha}{\sum}\phi_{\alpha}^{*}\phi'_{\alpha}}}
so Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle TrA=\int\underset{\alpha}{\prod}\frac{d\phi_{\alpha}^{*}d\phi_{\alpha}}{2\pi i}e^{-\underset{\alpha}{\sum}\phi_{\alpha}^{*}\phi{}_{\alpha}} \langle \phi|A|\phi\rangle}
as A is a function of creation and annihilation operators, namely Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(a_{\alpha}^{\dagger}, a_{\alpha})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\phi|A(a_{\alpha}^{+},a_{\alpha})|\phi \rangle= \langle\phi|A(\phi_{\alpha}^{*}, \phi_{\alpha}^{ \prime})|\phi \rangle= A(\phi_{\alpha}^{*}, \phi_{\alpha}^{ \prime})\langle\phi |\phi \rangle}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\phi_{\alpha}^{*}, \phi_{\alpha}^{ \prime})} is a combination of complex numbers.
Grassmann Algebra
Since annihilation and creation operators are anticommuted, we need anticommuting numbers to construct fermions coherent state using similar method as above. Because for fermions:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}a_{\beta}\left|\phi\right\rangle =-a_{\beta}a_{\alpha}\left|\phi\right\rangle =\phi_{\alpha}\phi_{\beta}\left|\phi\right\rangle =-\phi_{\beta}\phi_{\alpha}\left|\phi\right\rangle } ,
thus Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \phi_{\alpha},\phi_{\beta}\right\} =0} .
Also, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}^{2}\left|\phi\right\rangle=\phi_{\alpha}^{2}\left|\phi\right\rangle=0} ,
thus Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\alpha}^{2}=0}
From the examples above, we may find a kind of algebras for anticommuting numbers. Algebras of anticommuting numbers are called Grassmann algebras. It is very important to know that Boson coherent states are physical states, and the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} 's in the definition are c-numbers. But for Fermions, the variables of Grassmann Algebras are not physical numbers, they are usually operators. So the Fermion coherent states described in the following are not contained in the Fock space, and not physically observable.
We first define Grassman algebra by associating each generator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi_{\alpha}} with an annihilation operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}} . Similarly, a generator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi_{\alpha}^{*}} is associated with each creation operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}^{\dagger}} .
We then construct the generalized Fock space with coefficients in the Grassmann algebra:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\psi\right\rangle =\underset{\alpha}{\sum}\chi_{\alpha}\left|\phi_{\alpha}\right\rangle } ,
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{\alpha}} are grassman number and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\phi_{\alpha}\right\rangle } are vectors in Fock space.
The generators satisfy: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \xi_{\alpha},\xi_{\beta}\right\} =0.}
The basis of the Grassman algebra is made of all distinct products of the generators: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ 1;\xi_{\alpha_{1}},\xi_{\alpha_{2}},...,\xi_{\alpha_{n}};\xi_{\alpha_{1}}\xi_{\alpha_{2}},...;...;\xi_{\alpha_{1}}\xi_{\alpha_{2}}...\xi_{\alpha_{n}}\right\} } , where by convention the indices Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_{i}} are ordered Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_{1}<\alpha_{2}<...<\alpha_{n}} . The dimension is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{n}} . Any object within the Grassmann algebra is a linear combination of these bases. For example,a function of Grassmann variables is like: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\xi_{1},\xi_{2})=a_{0}+a_{11}\xi_{1}+a_{12}\xi_{2}+a_{2}\xi_{1}\xi_{2}} , which has only Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{2}} terms.
Conjugation:
In an algebra with even number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=2p} of generators, we can define a conjugation operation, by selecting of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} generators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi_{\alpha} } and to each we associate a generator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi_{\alpha}^{*}} :
the following properties define conjugation in a Grassmann algebra,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\xi_{\alpha})^{*}=\xi_{\alpha}^{*}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\xi_{\alpha}^{*})^{*}=\xi_{\alpha}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\lambda\xi_{\alpha})^{*}=\lambda^{*}\xi_{\alpha}^{*}} .
For any product of generators: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\xi_{\alpha_{1}}...\xi_{\alpha_{n}}\right)^{*}=\xi_{\alpha_{n}}^{*}\xi_{\alpha_{n-1}}^{*}...\xi_{\alpha\phi_{1}}^{*}} .
Derivative:
As for ordinary complex functions, a derivative can be defined for grassmann variable functions. It is defined to be identical to the complex derivative, except that in order for the derivative operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial\xi}} to act on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} , the variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} has to be anti-commuted through until it is adjacent to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial\xi}} .
ie.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial\xi}\xi=1; \frac{\partial}{\partial\xi}(\xi^{*}\xi)=-\xi; \frac{\partial}{\partial\xi}\lambda=0; \frac{\partial}{\partial\xi}(\xi\xi^{*})=\xi^{*}} ;
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\xi,\xi^{*})=a_{0}+a_{1}\xi+a_{1}^{*}\xi^{*}+a_{12}^{*}\xi^{*}\xi}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial\xi} f(\xi,\xi^{*}) = a_{1}+a_{12}\frac{\partial}{\partial\xi}(\xi^{*}\xi) =a_{1}+a_{12}[-\frac{\partial}{\partial\xi}(\xi\xi^{*})] =a_{1}-a_{12}\xi^{*}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial\xi}\xi^{*}\xi=-\xi^{*}, \frac{\partial}{\partial\xi^{*}}\xi^{*}\xi=-\xi}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial\xi}\frac{\partial}{\partial\xi^{*}}f(\xi,\xi^{*})=-a_{12}, \frac{\partial}{\partial\xi^{*}}\frac{\partial}{\partial\xi}f(\xi,\xi^{*})=a_{12}}
so Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \frac{\partial}{\partial\xi^{*}},\frac{\partial}{\partial\xi}\right\} =0.} it is anti-commuted.
Integral:
We define integration over grassmann variable as a linear mapping which has the fundamental property of order integrals over functions vanishing at infinity that the integral of an exact differential form is zero:
so: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi1=0} , and we define:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi\xi=1.}
also Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi^{*}1=0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi^{*}\xi^{*}=1} .
eg.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi f(\xi,\xi^{*})=\int d \xi (a_{0}+a_{1}\xi+a_{1}^{*}\xi^{*}+a_{12}^{*}\xi^{*}\xi)= 0+a_{1}+0+(-a_{12}\xi^{*})=a_{1}-a_{12}\xi^{*} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi^{*} f(\xi,\xi^{*})=a_{1}^{*}-a_{12}^{*}}
Grassmann Delta function:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta(\xi,\xi')=\int d\eta e^{-\eta(\xi-\xi')}=\int d\eta(1-\eta(\xi-\xi')).}
Prove: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi'\delta(\xi,\xi')f(\xi')=\int d\xi'\int d\eta(1-\eta(\xi-\xi'))f(\xi')=f(\xi).}
Scalar product of Grassmann functions:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle f|g\right\rangle =\int d\xi^{*}d\xi e^{-\xi^{*}\xi}f^{*}(\xi)g(\xi^{*})} ,
Since Grassmann numbers anticommute, any function of Grassmann numbers can only be expanded to the 1st order:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\xi)=f_{0}+f_{1}\xi, g(\xi)=g_{0}+g_{1}\xi} ,
and therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle f|g\right\rangle =\int d\xi^{*}d\xi (1- \xi^{*}\xi)(f_{0}^{*}+f_{1}^{*}\xi)(g_{0}+g_{1}\xi^{*})= f_{1}^{*}g_{1}\int d\xi^{*}d\xi \xi\xi^{*}-f_{0}^{*}g_{0}\int d\xi^{*}d\xi \xi^{*}\xi= f_{0}^{*}g_{0}+f_{1}^{*}g_{1}.}
Fermion coherent states
In order to construct coherent states, we must enlarge the Fermion Fock space.
Define a Grassmann algebra Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{G}} .
The difference from boson coherent states is due the necessary coefficients. For bosons, we may use only c-numbers, but for fermions it is necessary to use Grassmann numbers, so that the anticommutation relations will be preserved.
Any vector in the generalized Fock space is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\psi\right\rangle =\underset{\alpha}{\sum}\chi_{\alpha}\left|\phi_{\alpha}\right\rangle .}
We need to treat expressions containing combinations of Grassmann variables and creation and annihilation operators. So, we define: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \overset{\sim}{\xi},\overset{\sim}{a}\right\} =0} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\overset{\sim}{\xi}\overset{\sim}{a})^{\dagger}=\overset{\sim}{a}^{\dagger}\overset{\sim}{\xi}^{*}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{\sim}{\xi}} denotes any Grassmann variable in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \xi_{\alpha},\xi_{\alpha}^{*}\right\}} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{\sim}{a}} denotes any operator in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ a_{\alpha},a_{\alpha}^{\dagger}\right\} } .
Define a fermion coherent state: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\xi\right\rangle =e^{\underset{\alpha}{-\sum}\xi_{\alpha}a_{\alpha}^{_{\dagger}}}\left|0\right\rangle =\underset{\alpha}{\prod}(1-\xi_{\alpha}a_{\alpha}^{_{\dagger}})\left|0\right\rangle } .
Although the coherent state belongs to the generalized Fock space and not to \mathcal{F}, as we shall see, the crucial point is that any physical Fermion state of \mathcal{F} can be expanded in terms of these coherent states.
Proof that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\xi\right\rangle } is the eigenstate of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}:}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}(1-\xi_{\alpha}a_{\alpha}^{_{\dagger}})\left|0\right\rangle =\xi_{\alpha}a_{\alpha}a_{\alpha}^{_{\dagger}}\left|0\right\rangle =\xi_{\alpha}(\left\{ a_{\alpha},a_{\alpha}^{\dagger}\right\} -a_{\alpha}^{\dagger}a_{\alpha})\left|0\right\rangle =\xi_{\alpha}\left|0\right\rangle =\xi_{\alpha}(1-\xi_{\alpha}a_{\alpha}^{_{\dagger}})\left|0\right\rangle } .
So Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}\left|\xi\right\rangle =a_{\alpha}\underset{\beta}{\prod}(1-\xi_{\beta}a_{\beta}^{_{\dagger}})\left|0\right\rangle } .
for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha\neq\beta} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [1-\xi_{\alpha}a_{\alpha}^{_{\dagger}},1-\xi_{\beta}a_{\beta}^{_{\dagger}}]=\xi_{\alpha}a_{\alpha}^{_{\dagger}}\xi_{\beta}a_{\beta}^{_{\dagger}}-\xi_{\beta}a_{\beta}^{_{\dagger}}\xi_{\alpha}a_{\alpha}^{_{\dagger}}=0,} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [a_{\alpha},1-\xi_{\beta}a_{\beta}^{_{\dagger}}]=0,}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Longrightarrow a_{\alpha}\left|\xi\right\rangle =\underset{\beta\neq\alpha}{\prod}(1-\xi_{\beta}a_{\beta}^{_{\dagger}})a_{\alpha}(1-\xi_{\alpha}a_{\alpha}^{_{\dagger}})\left|0\right\rangle =\xi_{\alpha}\left|\xi\right\rangle .}
The adjoint of the coherent state: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \xi\right|=\left\langle 0\right|e^{\underset{\alpha}{-\sum}a_{\alpha}\xi_{\alpha}^{*}}=e^{\underset{\alpha}{\sum}\xi_{\alpha}^{*}a_{\alpha}},} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \xi\right|a_{\alpha}^{\dagger}=\left\langle \xi\right|\xi_{\alpha}^{*}.}
The action of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}^{\dagger} } on a coherent state:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha}^{\dagger}\left|\xi\right\rangle =-\frac{\partial}{\partial\xi}\left|\xi\right\rangle ,}
similarly, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \xi\right|a_{\alpha}=\frac{\partial}{\partial\xi^{*}}\left\langle \xi\right|.}
The overlap of the two coherent states (It is very important to remember that this is not Unity!):
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \xi|\xi'\right\rangle =\left\langle 0\right|\underset{\alpha}{\prod}(1+\xi{}_{\alpha}^{*}a_{\alpha}^{_{\dagger}})(1-\xi'_{\alpha}a_{\alpha}^{_{\dagger}})\left|0\right\rangle =\underset{\alpha}{\prod}(1+\xi{}_{\alpha}^{*}\xi'_{\alpha})=e^{\underset{\alpha}{\sum}\xi{}_{\alpha}^{*}\xi'_{\alpha}}} .
Unit operator:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\underset{\alpha}{\prod}d\xi_{\alpha}^{*}d\xi_{\alpha}e^{-\underset{\alpha}{\sum}\xi_{\alpha}^{*}\xi{}_{\alpha}}\left|\xi\right\rangle \left\langle \xi\right|=1.}
This is the unit operator in the physical Fermion Fock space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{F}} .
Proof:
Define operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=\int\underset{\alpha}{\prod}d\xi_{\alpha}^{*}d\xi_{\alpha}e^{-\underset{\alpha}{\sum}\xi_{\alpha}^{*}\xi{}_{\alpha}}\left|\xi\right\rangle \left\langle \xi\right|.}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \because\left\langle \alpha_{1},...,\alpha_{n}|\xi\right\rangle =\left\langle 0|a_{\alpha_{1}}...a_{\alpha_{n}}|\xi\right\rangle =\xi_{\alpha_{n}}...\xi_{\alpha_{1}},}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore\left\langle \alpha_{1},...,\alpha_{n}\right|A\left|\beta_{1},...,\beta_{n}\right\rangle =\int\underset{\alpha}{\prod}d\xi_{\alpha}^{*}d\xi_{\alpha}e^{-\underset{\alpha}{\sum}\xi_{\alpha}^{*}\xi{}_{\alpha}}\left\langle \alpha_{1},...,\alpha_{n}|\xi\right\rangle \left\langle \xi|\beta_{1},...,\beta_{n}\right\rangle=\int d\xi_{\alpha}^{*}d\xi_{\alpha}\underset{\alpha}{\prod}(1-\xi_{\alpha}^{*}\xi_{\alpha})\xi_{\alpha_{n}}...\xi_{\alpha_{1}}\xi_{\beta_{1}}^{*}...\xi_{\beta_{n}}^{*} } ,
since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi_{\gamma}^{*}d\xi_{\gamma}(1-\xi_{\gamma}^{*}\xi_{\gamma})\left\{ \begin{array}{c} \xi_{\gamma}\xi_{\gamma}^{*}\\ \xi_{\gamma}^{*}\\ \xi_{\gamma}\\ 1\end{array}\right\} =\left\{ \begin{array}{c} 1\\ 0\\ 0\\ 1\end{array}\right\} ,} all the states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} s are either occupied in both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \alpha_{1},...,\alpha_{n}\right|} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\beta_{1},...,\beta_{n}\right\rangle } or unoccupied in both states. This requires Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m=n} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\alpha_{1},...,\alpha_{n}\}} is some permutation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{ \beta_{1},...,\beta_{n}\right\} .} So write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi_{\alpha_{n}}...\xi_{\alpha_{1}}\xi_{\beta_{1}}^{*}...\xi_{\beta_{n}}^{*}=(-1)^{P}\xi_{\alpha_{n}}...\xi_{\alpha_{1}}\xi_{\alpha_{1}}^{*}...\xi_{\alpha_{n}}^{*}.} After this, all the necessary changes commute.
So Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \alpha_{1},...,\alpha_{n}\right|A\left|\beta_{1},...,\beta_{m}\right\rangle =\delta_{\alpha\beta}(-1)^{P}, } and the equality is established for any vectors in the Fock space.
Trace:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \because\left\langle \psi_{i}|\xi\right\rangle \left\langle \xi|\psi_{j}\right\rangle =\left\langle -\xi|\psi_{j}\right\rangle \left\langle \psi_{i}|\xi\right\rangle ,} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore TrA=\int\underset{\alpha}{\prod}d\xi_{\alpha}^{*}d\xi_{\alpha}e^{-\underset{\alpha}{\sum}\xi_{\alpha}^{*}\xi{}_{\alpha}}\left\langle -\xi\right|A\left|\xi\right\rangle } .
Gaussian Integrals
Here we prove 3 Identities for for multidimensional Gaussian integrals over 3 different kinds of variables:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty} \frac{dx_{1}...dx_{n} }{(2\pi)^{n/2}} e^{-\frac{1}{2}x_{i}A_{ij}x_{j}+x_{i}J_{j}}= [Det A]^{-1/2}e^{\frac{1}{2}J_{i}A^{-1}_{ij}J_{j}} ..........(GI1) }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{i}} are real variables and A is a real symmetric positive definite matrix. Summation over repeated indices is used throughout this subsection.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty} \underset{j=1}{\prod}^{n} \frac{dx^{*}_{j}dx_{j} }{2\pi i} e^{-x^{*}_{i}H_{ij}x_{j}+J^{*}_{i}x_{i}+J_{i}x^{*}_{i}}= [Det H]^{-1}e^{J^{*}_{i}H^{-1}_{ij}J_{j}} ..........(GI2) }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{i}} are complex variables and H is a positive Hermitian matrix.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty} \underset{j=1}{\prod}^{n} d\eta^{*}_{j}d\eta_{j} e^{-\eta^{*}_{i}H_{ij}\eta_{j}+\xi^{*}_{i}\eta_{i}+\xi_{i}\eta^{*}_{i}}= [Det H]e^{\xi^{*}_{i}H^{-1}_{ij}\xi_{j}} ..........(GI3) }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi_{i}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta_{i}} are Grassmann variables and H is a Hermitian but not necessary positive definite matrix.
Proof of GI1
The idea is making change of variables so that the matrix reduces to diagonal form and then we can use the familiar Gaussian Integral
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty} dx e^{-ax^{2}}=\sqrt{\frac{\pi}{a}} }
to obtain the result. we first perform transformation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{i}=x_{i}-A^{-1}_{ij}J_{j} } , and then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{k}=O^{-1}_{ki}y_{i} } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O } is orthogonal transformation which diagonalize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A } with eignvalues Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{1},a_{2},...,a_{n} } . So we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int_{-\infty}^{\infty} \frac{dx_{1} ...dx_{n} }{(2\pi)^{n/2}} e^{-\frac{1}{2}x_{i}A_{ij}x_{j}+x_{i}J_{j}}&= \int_{-\infty}^{\infty} \frac{dy_{1}...dy_{n} }{(2\pi)^{n/2}} e^{-\frac{1}{2}y_{i}A_{ij}y_{j}+\frac{1}{2}J_{a}A^{-1}_{ab}J_{b} } \\ & = \int_{-\infty}^{\infty} \frac{dz_{1}...dz_{n} }{(2\pi)^{n/2}} e^{ -\frac{1}{2}a_{1}z^{2}_{1}-\frac{1}{2}a_{2}z^{2}_{2}... -\frac{1}{2}a_{n}z^{2}_{n} +\frac{1}{2}J_{a}A^{-1}_{ab}J_{b} } \\ &= \frac{1}{(2\pi)^{n/2}} \int_{-\infty}^{\infty}dz_{1} e^{-\frac{1}{2}a_{1}z^{2}_{1}} \int_{-\infty}^{\infty}dz_{2} e^{-\frac{1}{2}a_{2}z^{2}_{2}}... \int_{-\infty}^{\infty}dz_{n} e^{-\frac{1}{2}a_{n}z^{2}_{n}} e^{\frac{1}{2}J_{a}A^{-1}_{ab}J_{b}} \\ &= \frac{1}{(2\pi)^{n/2}} \sqrt{\frac{2\pi}{a_{1}}}... \sqrt{\frac{2\pi}{a_{n}}} e^{\frac{1}{2}J_{i}A^{-1}_{ij}J_{j}} \\ &=\frac{1}{\sqrt{a_{1}a_{2}...a_{n}}}e^{\frac{1}{2}J_{i}A^{-1}_{ij}J_{j}} \\ &= [Det A]^{-1/2}e^{\frac{1}{2}J_{i}A^{-1}_{ij}J_{j}} \end{align}}
Note that the positivity of A is essential for the convergence of the Gaussian integral.
Proof of GI2
Following similar idea. First perform transformation
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_{i}=x_{i}-H^{-1}_{ij}J_{j} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y^{*}_{i}=x^{*}_{i}-H^{-1}_{ij}J^{*}_{j} } , and then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{k}=O^{-1}_{ki}y_{i} } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O } is orthogonal transformation which diagonalize H with eignvalues Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{1},a_{2},...,a_{n} } . So we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int_{-\infty}^{\infty} \underset{j=1}{\prod}^{n} \frac{dx^{*}_{j}dx_{j} }{2\pi i} e^{-x^{*}_{i}H_{ij}x_{j}+J^{*}_{i}x_{i}+J_{i}x^{*}_{i}} &= \int_{-\infty}^{\infty} \underset{j=1}{\prod}^{n} \frac{dy^{*}_{j}dy_{j} }{2\pi i} e^{-y^{*}_{i}H_{ij}y_{j}+J^{*}_{a}H^{-1}_{ab}J_{b} } \\ & = \int_{-\infty}^{\infty} \underset{j=1}{\prod}^{n} \frac{dz^{*}_{j}dz_{j} }{2\pi i} e^{ -a_{1}z^{*}_{1}z_{1}-a_{2}z^{*}_{2}z_{2}... -a_{n}z^{*}_{n}z_{n} +J^{*}_{a}H^{-1}_{ab}J_{b} } \\ & =\int_{-\infty}^{\infty} \underset{j=1}{\prod}^{n} \left\{\frac{dRe z_{j}dIm z_{j} }{\pi } e^{ -a_{j}[(Re z_{j})^{2}+(Im z_{j})^{2}]}\right\} e^{J^{*}_{a}H^{-1}_{ab}J_{b}} \\ & = \underset{j=1}{\prod}^{n} \left\{ \int_{-\infty}^{\infty} \frac{dRe z_{j} }{\sqrt{\pi} } e^{ -a_{j}(Re z_{j})^{2}}\right\} \left\{ \int_{-\infty}^{\infty} \frac{dIm z_{j} }{\sqrt{\pi} } e^{ -a_{j}(Im z_{j})^{2}}\right\} e^{J^{*}_{a}H^{-1}_{ab}J_{b}} \\ &=\frac{1}{a_{1}a_{2}...a_{n}}e^{J^{*}_{i}H^{-1}_{ij}J_{j}}\\ &= [Det H]^{-1}e^{J^{*}_{i}H^{-1}_{ij}J_{j}} \end{align}}
Proof of GI3
First we note that the Gaussian integral involving a single pair of conjugate Grassmann variable is evaluated as follow:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi^{*} d\xi e^{-\xi^{*}a \xi} = \int d\xi^{*} d\xi(1-\xi^{*}a\xi)=a }
Note that for single variable, the Gaussian integral involve Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a } in contrast to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{a}} as we obtain in original Gaussian integral. So if we could bring the multi-variable Gaussian integral into diagonal form, we would expect to get a similar result involving the product of the eigenvalues, and thus the determinant of H, in the numerator instead of the denominator as for complex variables.
Second, we need to derive the law for the linear transformation of Grassmann variables. Assume
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi^{*}_{1} d\xi_{1} ... d\xi^{*}_{n} d\xi_{n} P(\xi^{*},\xi)= J \int d\eta^{*}_{1} d\eta_{1} ... d\eta^{*}_{n} d\eta_{n} P(\xi^{*}(\eta^{*},\eta) ,\xi(\eta^{*},\eta)) }
Relabel the variables as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\xi^{*}_{1},\xi^{*}_{2},... \xi^{*}_{n},\xi_{n},....,\xi_{2},\xi_{1})= \overset{\sim}{\xi_{1}},\overset{\sim}{\xi_{1}}...,\overset{\sim}{\xi_{2n}} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\eta^{*}_{1},\eta^{*}_{2},... \eta^{*}_{n},\eta_{n},....,\eta_{2},\eta_{1})= \overset{\sim}{\eta_{1}},\overset{\sim}{\eta_{1}}...,\overset{\sim}{\eta_{2n}} }
writing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{\sim}{\xi_{i}} = M_{ij} \overset{\sim}{\eta_{i}} }
Since the only non-vanishing terms in the integral come from the term containing every Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{\sim}{\xi} } as a factor one times, so we can write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(\xi^{*},\xi) = p \underset{i=1}{\prod}^{2n} \overset{\sim}{\xi_{i}} }
So we rewrite the integral as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi^{*}_{1} d\xi_{1} ... d\xi^{*}_{n} d\xi_{n} p \underset{i=1}{\prod}^{2n} \overset{\sim}{\xi_{i}} = J \int d\eta^{*}_{1} d\eta_{1} ... d\eta^{*}_{n} d\eta_{n} p \underset{i=1}{\prod}^{2n} (\sum_{j} M_{ij} \overset{\sim}{\eta_{j}}) }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int d\xi^{*}_{1} d\xi_{1} ... d\xi^{*}_{n} d\xi_{n} p \underset{i=1}{\prod}^{2n} \overset{\sim}{\xi_{i}} &= J \int d\eta^{*}_{1} d\eta_{1} ... d\eta^{*}_{n} d\eta_{n} p \underset{i=1}{\prod}^{2n} (\sum_{j} M_{ij} \overset{\sim}{\eta_{j}}) \\ p(-1)^{n} &= J \int d\eta^{*}_{1} d\eta_{1} ... d\eta^{*}_{n} d\eta_{n} p \underset{i=1}{\prod}^{2n} (\sum_{j} M_{ij} \overset{\sim}{\eta_{j}}) \\ &= J \int d\eta^{*}_{1} d\eta_{1} ... d\eta^{*}_{n} d\eta_{n} p \underset{P} \sum \underset{i=1} {\prod}^{2n} M_{iP_{i}} \overset{\sim}{\eta_{P_{i}}} \\ &= Jp \underset{P} \sum\underset{i=1} {\prod}^{2n} M_{iP_{i}}(-1)^{P} \int d\eta^{*}_{1} d\eta_{1} ... d\eta^{*}_{n} d\eta_{n} \overset{\sim}{\eta_{1}},\overset{\sim}{\eta_{1}}...,\overset{\sim}{\eta_{2n}} \\ &=JpDet M (-1)^{n} \end{align}}
So we get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J=[Det M]^{-1}=\left|\frac{\partial(\eta^{*},\eta)}{\partial(\xi^{*},\xi)}\right| }
So the linear transformation law for Grassmann variable is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d\xi^{*}_{1} d\xi_{1} ... d\xi^{*}_{n} d\xi_{n} P(\xi^{*},\xi)= \left|\frac{\partial(\eta^{*},\eta)}{\partial(\xi^{*},\xi)}\right| \int d\eta^{*}_{1} d\eta_{1} ... d\eta^{*}_{n} d\eta_{n} P(\xi^{*}(\eta^{*},\eta) ,\xi(\eta^{*},\eta)) }
which is different from the transformation law for complex variable by the appearance of the inverse of the Jacobian instead of Jacobian.
Now to prove GI3, we perform transformation
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{i} = \eta_{i} - H^{-1}_{ij}\xi_{j} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^{*}_{i} = \eta^{*}_{i} - (H^{-1}_{ij})^{*}\xi^{*}_{j} }
Then diagonalizing H with unitary transformation and define
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{i} = U^{-1}_{ij}\rho_{j} }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int_{-\infty}^{\infty} \underset{j=1}{\prod}^{n} d\eta^{*}_{j}d\eta_{j} e^{-\eta^{*}_{i}H_{ij}\eta_{j}+\xi^{*}_{i}\eta_{i}+\xi_{i}\eta^{*}_{i}} &= \int_{-\infty}^{\infty} \underset{j=1}{\prod}^{n} d\rho^{*}_{j}d\rho_{j} e^{-\rho^{*}_{i}H_{ij}\rho_{j}} e^{\xi^{*}_{a}H^{-1}_{ab}\xi_{b}} \\ &= \int_{-\infty}^{\infty} \underset{j=1}{\prod}^{n} d\chi^{*}_{j}d\chi_{j} e^{-\sum_{j}h_{j}\chi^{*}_{j}\chi_{j}} e^{\xi^{*}_{a}H^{-1}_{ab}\xi_{b}}\\ &= ( \underset{j=1}{\prod}^{n} h_{j}) e^{\xi^{*}_{a}H^{-1}_{ab}\xi_{b}} \\ &=[Det H] e^{\xi^{*}_{i}H^{-1}_{ij}\xi_{j}} \end{align}}
To summarize the identity operator and trace of an operator for bosons and fermions:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int\underset{\alpha}{\prod}\frac{d\phi_{\alpha}^{*}d\phi_{\alpha}}{N}e^{-\underset{\alpha}{\sum}\phi_{\alpha}^{*}\phi{}_{\alpha}}\left|\phi\right\rangle \left\langle \phi\right|=1}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=\lbrace^{2 \pi i\qquad bosons}_{1\qquad fermions}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle TrA=\int\underset{\alpha}{\prod}\frac{d\phi_{\alpha}^{*}d\phi_{\alpha}}{N}e^{-\underset{\alpha}{\sum}\phi_{\alpha}^{*}\phi{}_{\alpha}}\langle\varsigma \phi\vert A\vert\phi\rangle}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varsigma=\lbrace^{+1i\qquad bosons}_{-1\qquad fermions}}
Field integral for the quantum partition function
Partition function for a quantum many-body system
Having introduced the coherent states, the construction of path integrals for many-body systems no longer presents substantial difficulties. In this section we will see that much of the information on quantum many-particle systems is encoded in expectation values of products of creation and annihilation operators,i.e. expressions of the structure Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle a^{+}a\dotsb\rangle} ,By an analogy to be explained then, objects of this type are generally called correlation functions. More important for our present discussion, at any finite temperature, the average Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\dotsb\rangle} entering the definition of the correlation function runs over the quantum Gibbs distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\rho}= \frac{e^{-\beta(\hat{H}-\mu\hat{N})}}{Z}} , where, as usual,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z= Tr[e^{-\beta(\hat{H}-\mu\hat{N})}]=\sum\limits_{n} \langle n\vert e^{-\beta(\hat{H}-\mu\hat{N})}\vert n \rangle}
is the quantum partition function,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta /T, \mu } denotes the chemical potential, and the sum extends over a complete set of Fock space states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\vert n \rangle\}} .
ultimately, we want to evaluate the path integral representations of correlation functions.The partition function is of importance in its own right, as it contains much of the information needed to characterize the thermodynamic properties of a many-body quantum system, let us first get into many-body field theory with a construction of the path integral.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z= Tr[e^{-\beta(\hat{H}-\mu\hat{N})}]=\sum\limits_{n} \langle n\vert e^{-\beta(\hat{H}-\mu\hat{N})}\vert n \rangle}
Insert the identity operator, we get:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\frac{1}{Tr[e^{-\beta\hat{(H}-\mu \hat{N})}]}=\int \prod_{\alpha }\frac{d\phi^{*} _{\alpha }d\phi _{\alpha }}{N}e^{-\sum_{\alpha }\phi^{*} _{\alpha }\phi _{\alpha}}<\xi \phi \mid e^{-\beta\hat{(H}-\mu \hat{N})}\mid \phi >}
Partition function for many particle system
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=Tr[e^{-\beta(\hat{H}-\mu\hat{N})}]} , now we expand Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta=\epsilon M} , and take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon\rightarrow 0} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\rightarrow\infty} , therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta } evolves as “imaginary time”:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\beta(\hat{H}-\mu\hat{N})}=e^{-\epsilon(\hat{H}-\mu)}\mathbb{I}e^{-\epsilon(\hat{H}-\mu)}\mathbb{I}...\mathbb{I}e^{-\epsilon(\hat{H}-\mu)}} ,
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{I}=\int\prod_{\alpha}\frac{d\phi_{\alpha}^{*}d\phi_{\alpha}}{N}e^{-\sum_{\alpha}\phi_{\alpha}^{*}\phi_{\alpha}}<\xi|\xi>} .
here are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M-1} terms sandwiched between the imaginary time slicing. A generic term will look like
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi_{k+1}|1-\epsilon(\hat{H}-\mu\hat{N})+\mathcal{O}(\epsilon^{3})|\phi_{k}\right\rangle =\left\langle \phi_{k+1}|1-\epsilon(H-\mu N)(\phi_{k+1}^{*},\phi_{k})+\mathcal{O}(\epsilon^{3})|\phi_{k}\right\rangle} ,
the left hand side is already in normal order.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =e^{-\epsilon(H-\mu N)}(\phi_{k+1}^{*},\phi_{k})\left\langle \phi_{k+1}|\phi_{k}\right\rangle +\mathcal{O}(\epsilon^{3})} .
Now we calculate:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \zeta\phi|e^{-\beta(\hat{H}-\mu\hat{N})}|\phi\right\rangle =\int\prod_{k=1}^{M-1}\prod_{\alpha}\frac{d\phi_{\alpha,k}^{*}d\phi_{\alpha,k}}{N}e^{-\sum_{k=1}^{M-1}\sum_{\alpha}\phi_{\alpha,k}^{*}\phi_{\alpha,k}}\left\langle \zeta\phi|e^{-\beta(\hat{H}-\mu\hat{N})}|\phi_{M-1}\right\rangle \left\langle \phi_{M-1}|e^{-\beta(\hat{H}-\mu\hat{N})}|\phi_{M-2}\right\rangle ...\times}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \phi_{2}|e^{-\beta(\hat{H}-\mu\hat{N})}|\phi_{1}\right\rangle \left\langle \phi_{1}|e^{-\beta(\hat{H}-\mu\hat{N})}|\phi\right\rangle >=\int\prod_{k=1}^{M-1}\prod_{\alpha}\frac{d\phi_{\alpha,k}^{*}d\phi_{\alpha,k}}{N}e^{-\sum_{k=1}^{M-1}\sum_{\alpha}\phi_{\alpha,k}^{*}\phi_{\alpha,k}}e^{-\sum_{\alpha}\zeta\phi_{\alpha,1}^{*}\phi_{\alpha,M-1}}e^{-\epsilon(\hat{H}-\mu\hat{N})(\zeta\phi_{1}^{*},\phi_{M-1})}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\sum_{\alpha}\phi_{\alpha,M-1}^{*}\phi_{\alpha,M-2}}e^{-\epsilon(\hat{H}-\mu\hat{N})(\zeta\phi_{M-1}^{*},\phi_{M-2})}...e^{-\sum_{\alpha}\phi_{\alpha,1}^{*}\phi_{\alpha}}e^{-\epsilon(\hat{H}-\mu\hat{N})(\zeta\phi_{1}^{*},\phi)}}
Because each of the terms containing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} commute , we can write as exponent of sums: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon\sum\{\phi_{\alpha,M}^{*}\frac{\left(\phi_{\alpha,M-1}^{*}-\phi_{\alpha,M}\right)}{\epsilon}+\phi_{\alpha,M-1}^{*}\frac{\left(\phi_{\alpha,M-2}^{*}-\phi_{\alpha,M-1}\right)}{\epsilon}+...+\phi_{\alpha,1}^{*}\frac{\left(\phi_{\alpha,0}^{*}-\phi_{\alpha,1}\right)}{\epsilon}-\left[H\phi_{\alpha,M}^{*}\zeta\phi_{\alpha,M-1}-\mu\phi_{\alpha,M}^{*}\zeta\phi_{\alpha,M-1}\right]-} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[H\phi_{\alpha,M-1}^{*}\zeta\phi_{\alpha,M-2}-\mu\phi_{\alpha,M-1}^{*}\zeta\phi_{\alpha,M-2}\right]-...-\left[H\phi_{\alpha,1}^{*}\zeta\phi_{\alpha,M}-\mu\phi_{\alpha,1}^{*}\zeta\phi_{\alpha,M}\right]\}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta\phi_{\alpha,M}=\phi_{\alpha,0}} . This looks like a Reimann Sum. At each time slice, involve product over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\alpha}^{*}\phi_{\alpha}} . By using the notation that:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial \tau} \phi_{\alpha,M} = \frac{\phi_{\alpha, M-1} - \phi_{\alpha,M}}{\epsilon} }
The complicated integral of Operator and states reduces into :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int\limits_{\phi_{\alpha(\beta)}=\varsigma\phi (0)} D\left[\phi_{\alpha}^{*}(\tau)\phi_{\alpha}(\tau)\right]e^{-\int_{0}^{\beta}d\tau\sum_{\alpha}\left[\phi_{\alpha}^{*}(\tau)\left(\frac{\partial}{\partial\tau}-\mu\right)\phi_{\alpha}(\tau)+H(\phi_{\alpha}^{*}(\tau),\phi_{\alpha}(\tau))\right]}}
Note that the differential notation above is not exactly correct; there is no necessary condition that the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\alpha,i}} 's be continuous in any sense. It turns out that the continuum representation is quite useful, but at times must be discarded in favor of the exact meaning.
In the beginning, we consider there is interaction term in Hamiltonian of the many-body system:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(\phi_{\alpha}^{*}(\tau), \phi_{\alpha}(\tau))= \sum\limits_{\alpha}\epsilon_{\tau}\phi_{\alpha}^{*}(\tau) \phi_{\alpha}(\tau)}
Partition function is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{0}=\int\limits_{\phi_{\alpha(\beta)}=\varsigma\phi (0)} D\left[\phi_{\alpha}^{*}(\tau)\phi_{\alpha}(\tau)\right]e^{-\int_{0}^{\beta}d\tau\sum_{\alpha}\left[\phi_{\alpha}^{*}(\tau)\left(\frac{\partial}{\partial\tau}+\epsilon_{\alpha}-\mu\right)\phi_{\alpha}(\tau) \right]}}
If there is an interacting term:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(\phi_{\alpha}^{*}(\tau) \phi_{\beta}^{*}(\tau),\dotsb\phi_{\gamma}^{*}(\tau)\phi_{\iota}^{*}(\tau) )}
Correspondingly, the partition function with interacting term is: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=Z_{0}\frac{\int\limits_{\phi_{\alpha(\beta)}=\varsigma\phi (0)} D\left[\phi_{\alpha}^{*}(\tau)\phi_{\alpha}(\tau)\right]e^{-\int_{0}^{\beta}d\tau\sum_{\alpha}\left[\phi_{\alpha}^{*}(\tau)\left(\frac{\partial}{\partial\tau}+\epsilon_{\alpha}-\mu\right)\phi_{\alpha}(\tau) \right]} e^{-\int_{0}^{\beta}d \tau V}}{\int\limits_{\phi_{\alpha(\beta)}=\varsigma\phi (0)} D\left[\phi_{\alpha}^{*}(\tau)\phi_{\alpha}(\tau)\right]e^{-\int_{0}^{\beta}d\tau\sum_{\alpha}\left[\phi_{\alpha}^{*}(\tau)\left(\frac{\partial}{\partial\tau}+\epsilon_{\alpha}-\mu\right)\phi_{\alpha}(\tau) \right]}}= Z_{0} \langle e^{-\int_{0}^{\beta} d \tau V} \rangle = Z_{0} ( \langle 1 \rangle - \int_{0}^{\beta}d \tau \langle V \rangle + \frac{1}{2!} \int_{0}^{\beta}d \tau\int_{0}^{\beta}d \tau^{\prime}\langle V^{2} \rangle+ \dotsb }
Wick's theorem is needed to solve this problem. We will define it and prove it in the following.
quantum partition function without interaction
Please refer to Thermal(imaginary-time) Green's function Section,this section is made based on part of that section.
Let's calculate the partition function of free bosons/fermions, without interaction term in the Hamiltonian:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{\alpha}\varepsilon_{\alpha}a_{\alpha}^{+}a_{\alpha}}
The partition function is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D(\Phi_{\alpha}^{*}(\tau),\Phi_{\alpha}(\tau))e^{-\int_{0}^{\beta}d\tau L_{0}}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{\alpha}(\beta)=\xi\Phi_{\alpha}(0)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{0}(\tau)=\sum_{\alpha}(\Phi(\tau)(\frac{\partial}{\partial\tau}+\varepsilon_{\alpha}-\mu)\Phi_{\alpha}(\tau)}
So,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{\beta}d\tau L(\tau)=\sum_{\alpha}(\sum_{k=2}^{m}\Phi_{\alpha,k}^{*}(\Phi_{\alpha,k}-\Phi_{\alpha,k-1}+\frac{\beta}{m}(\varepsilon_{\alpha}-\mu)\Phi_{\alpha,k-1})+\Phi_{\alpha,1}^{*}(\Phi_{\alpha,1}-\xi\Phi_{\alpha,m}+\frac{\beta}{m}(\varepsilon_{\alpha}-\mu)\xi\Phi_{\alpha,m}))}
Above we have used the the method that :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\beta H}=e^{-\Delta \varepsilon H}e^{-\Delta \varepsilon H}\cdots e^{-\Delta \varepsilon H}}
where,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\Delta \varepsilon=\beta} . Then we can express Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z} in terms of product of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{\beta}d\tau L(\tau)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=lim_{m\rightarrow\infty}\prod_{\alpha}(\int\prod_{k=1}^{m}\frac{d\Phi_{k}^{*}d\Phi_{k}}{N}e^{-\Phi_{i}^{*}S_{ij}^{(\alpha)}\Phi_{j}})}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{ij}^{(\alpha)}=\left(\begin{array}{ccccc} 1 & 0 & .... & .. & -\xi\lambda\\ -\lambda & 1 & 0 & ... & 0\\ 0 & -\lambda & 1 & 0.... & 0\\ ... & .. & -\lambda & .. & ..\\ .. & .. & .. & -\lambda & 1\end{array}\right)_{m\times m} } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=1-\frac{\beta}{m}(\varepsilon_{\alpha}-\mu).}
So we can calculate the partition function:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=lim_{m\rightarrow\infty}\prod_{\alpha}(Det(S_{ij}^{(\alpha)}))^{-\xi}}
And Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Det(S^{\alpha})=1 Det \left(\begin{array}{ccccc} 1 & 0 & .. & .. & ..\\ -\lambda & 1 & .. & .. & ..\\ 0 & -\lambda & 1 & .. & ..\\ ..& .. & .. & .. & ..\\ 0 & .. & .. & .. & -\lambda\end{array}\right)_{(m-1)\times(m-1)} + (-1)^{m-1}(-\xi\lambda)Det \left(\begin{array}{ccccc} -\lambda & 1 & .. & .. & 0\\ 0 & -\lambda & 1 & .. & 0\\ ..& .. & .. & .. & ..\\ ..& .. & .. & .. & ..\\ 0 & .. & .. & .. & -\lambda\end{array}\right)_{(m-1)\times(m-1)} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =1+(-1)^{M}\xi\lambda(-\lambda)^{M-1}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =1-\xi\lambda^{M}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =1-\xi(1-\frac{\beta}{M}(\varepsilon_{\alpha}-\mu)^{M}}
Finally,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\prod_{\alpha}lim_{m\rightarrow\infty}(1-\xi\lambda^{m})^{-\xi}=\prod_{\alpha}(1-\xi e^{-\beta(\varepsilon_{\alpha}-\mu)})}
We have got the partition which is the same form as we learned in Statistical Mechanics.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\begin{cases} \begin{array}{cc} \prod_{\alpha}\frac{1}{1-e^{-\beta(\varepsilon_{\alpha}-\mu)}} & boson\\ \prod_{\alpha}(1+e^{-\beta(\varepsilon_{\alpha}-\mu)}) & fermions\end{array}\end{cases}}
Wick's theorem
We want to compute quantities like the expectation value of time ordered products. The ordering of the operators is fixed by T, time ordering operator. But our Hamiltonian especially the interaction part of it, contains a lot of creation and annihilation operators. One way to deal with this is to move all annihilation operators to the right and creation operators to the left. This is taking care of by using the so-called normal ordering. Wick's theorem is the link between time ordered products to normal ordered products. It's of great importance both in Solid State Physics as well as in Particle Physics.
It is named after Gian-Carlo Wick. The most important notion that someone will encounter studying and then applying it, is the notion of contraction. Let's define it first and then prove it.
Definition:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\int D[\psi^{*},\psi]\xi_{i1}\psi_{i2}...\psi_{in}\psi_{jn}^{*}...\psi_{j2}^{*}\psi_{j1}^{*}e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}}{\int D[\psi^{*}\psi]e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}}=\sum_{p}\xi^{p}M_{ip_{n},j_{n}}^{-1}M_{ip_{n-1},j_{n-1}}^{-1}...M_{ip_{1},j_{1}}^{-1}}
to prove this theorem, we assume a generating function like below that we know its value(by referring to the Gaussian Integrals). The following proof is slightly different than the proof in Particle Physics (and Quantum Field Theory) which proceeds by induction, but our proof here is better adjusted to our needs:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(J^{*},J)=\frac{\int D(\psi^{*},\psi)e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}e^{\sum\limits_{i}(J_{i}^{*}\psi_{i}+\psi_{i}^{*}J_{i})}}{\int D(\psi^{*},\psi)e^{\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}}=e^{\sum\limits_{i,j}J_{i}^{*}M_{i,j}^{-1}J_{j}}}
Now, we take the derivatives from both sides and then set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J=J^{*}=0} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta^{n}G(J^{*},J)}{\delta J_{i1}^{*}\dotsb\delta J_{in}^{*}\delta J_{j1}\dotsb\delta J_{jn}} =\varsigma^{n} \frac{\int D(\psi^{*},\psi)\psi_{jn}^{*}\dotsb\psi_{j2}^{*}\psi_{j1}^{*}e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}e^{\sum\limits_{i}(J_{i}^{*}\psi_{i}+\psi_{i}^{*}J_{i})}}{\int D(\psi^{*},\psi)e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta^{2n}G(J^{*},J)}{\delta J_{i1}^{*}\dotsb\delta J_{in}^{*}\delta J_{j1}\dotsb\delta J_{jn}} =\varsigma^{n} \frac{\int D(\psi^{*},\psi)\psi_{i1}\psi_{i2}\dotsb\psi_{in} \psi_{jn}^{*}\dotsb\psi_{j2}^{*}\psi_{j1}^{*}e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}e^{\sum\limits_{i}(J_{i}^{*}\psi_{i}+\psi_{i}^{*}J_{i})}}{\int D(\psi^{*},\psi)e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}}}
So, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta^{2n}G(J^{*},J)}{\delta J_{i1}^{*}\dotsb\delta J_{in}^{*}\delta J_{j1}\dotsb\delta J_{jn}}\mid_{J=J^{*}=0} =\varsigma^{n} \frac{\int D(\psi^{*},\psi)\psi_{i1}\psi_{i2}\dotsb\psi_{in}\psi_{jn}^{*}\dotsb\psi_{j2}^{*}\psi_{j1}^{*}e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}}{\int D(\psi^{*},\psi)e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}}}
For the right hand side:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\delta^{2n}}{\delta J_{i1}^{*}...\delta J_{in}^{*}\delta J_{j1}...\delta J_{jn}}e^{\sum\limits_{i,j}J_{i}^{*}M_{i,j}^{-1}J_{j}}=\frac{\delta^{n}}{\delta J_{i1}^{*}...\delta J_{in}^{*}}(\sum\limits_{k_{n}}J_{k_{n}}^{*}M_{k_{n},j_{n}}^{-1})...(\sum\limits_{k_{2}}J_{k_{2}}^{*}M_{k_{2},j_{2}}^{-1})(\sum\limits_{k_{1}}J_{k_{1}}^{*}M_{k_{1},j_{1}}^{-1})}
In sum, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\int D[\psi^{*},\psi]\xi_{i1}\psi_{i2}...\psi_{in}\psi_{jn}^{*}...\psi_{j2}^{*}\psi_{j1}^{*}e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}}{\int D[\psi^{*}\psi]e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}}=\sum_{p}\xi^{p}M_{ip_{n},j_{n}}^{-1}M_{ip_{n-1},j_{n-1}}^{-1}...M_{ip_{1},j_{1}}^{-1}}
Quantum partition function with interaction
Path integral with interaction
Let us construct the Hamiltonian in many-body system, where there are interaction.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=H_{0}+H_{int}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}=\sum\limits_{\alpha}(\epsilon_{\alpha}-\mu)c_{\alpha}^{+} (r,\tau)c_{\alpha}(r,\tau)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{int}=V=\sum\limits_{r,r^{\prime}}V_{r-r^{\prime}}c_{r}^{*}(\tau)c_{r^{\prime}}^{*}(\tau)c_{r^{\prime}}(\tau)c_{r}^{*}(\tau)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=Z_{0}\frac{\int\limits_{\phi_{\alpha(\beta)}=\varsigma\phi (0)} D\left[\phi_{\alpha}^{*}(\tau)\phi_{\alpha}(\tau)\right]e^{-\int_{0}^{\beta}d\tau\sum_{\alpha}\left[\phi_{\alpha}^{*}(\tau)\left(\frac{\partial}{\partial\tau}+\epsilon_{\alpha}-\mu\right)\phi_{\alpha}(\tau) \right]} e^{-\int_{0}^{\beta}d \tau V}}{\int\limits_{\phi_{\alpha(\beta)}=\varsigma\phi (0)} D\left[\phi_{\alpha}^{*}(\tau)\phi_{\alpha}(\tau)\right]e^{-\int_{0}^{\beta}d\tau\sum_{\alpha}\left[\phi_{\alpha}^{*}(\tau)\left(\frac{\partial}{\partial\tau}+\epsilon_{\alpha}-\mu\right)\phi_{\alpha}(\tau) \right]}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int\limits_{\phi_{\alpha(\beta)}=\varsigma\phi (0)} D\left[\phi_{\alpha}^{*}(\tau)\phi_{\alpha}(\tau)\right]e^{-\int_{0}^{\beta}d\tau\sum_{\alpha}\left[\phi_{\alpha}^{*}(\tau)\left(\frac{\partial}{\partial\tau}+\epsilon_{\alpha}-\mu\right)\phi_{\alpha}(\tau) \right]} e^{-\int_{0}^{\beta}d \tau V}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int\limits_{\phi_{\alpha(\beta)}=\varsigma\phi (0)} D\left[\phi_{\alpha}^{*}(\tau)\phi_{\alpha}(\tau)\right]e^{-\int_{0}^{\beta}d\tau H}}
Then in partition function, the action is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=\int_{0}^{\beta}d\tau H=\int_{0}^{\beta}d\tau H_{0}+ H_{int}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{0}=\int_{0}^{\beta}d\tau H_{0}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{int}=\int_{0}^{\beta}d\tau H_{int}}
Using fourier transform, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{r}(\tau)=\frac{1}{\beta}\sum\limits_{\omega_{n}}e^{-i\omega_{n}\tau}\frac{1}{\sqrt{L^{3}}}\sum\limits_{\vec{k}}e^{i\vec{k}\vec{r}}c(k,i\omega)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{0}=\int_{0}^{\beta}d\tau H_{0}=\frac{1}{\beta}\sum\limits_{\omega_{n},k}(-i\omega_{n}+\epsilon_{k}-\mu)c^{*}(k,i\omega_{n})c(k,i\omega_{n})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{int}=\int_{0}^{\beta}d\tau H_{int}=\frac{1}{\beta^{3}}\sum\limits_{\omega_{n},\Omega_{n},\nu_{n}}\frac{1}{L^{3}}\sum\limits_{k,q,p}V_{q}c^{*}(k,i\omega_{n})c^{*}(p,i\nu_{n})c(p+q,i\nu_{n}+i\Omega_{n})c(k-q,i\omega_{n}-i\Omega_{n})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{Z}{Z_{0}}=<e^{-S_{int}}>=<1-S_{int}+\frac{1}{2!}S_{int}^{2}-\frac{1}{3!}S_{int}^{3}+\dotsb>=1-<S_{int}>+<\frac{1}{2!}S_{int}^{2}>-<\frac{1}{3!}S_{int}^{3}>+<\dotsb>}
Just considering the interaction term is very small, just focus on the leading term,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <S_{int}>=<\frac{1}{\beta^{3}}\sum\limits_{\omega_{n},\Omega_{n},\nu_{n}}\frac{1}{L^{3}}\sum\limits_{k,q,p}V_{q}c^{*}(k,i\omega_{n})c^{*}(p,i\nu_{n})c(p+q,i\nu_{n}+i\Omega_{n})c(k-q,i\omega_{n}-i\Omega_{n})>}
In Green Function chapter, we can get the thermal Green's Function for two operators,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <T_{\tau}a_{\alpha}^{(H)}(\tau)a_{\beta}^{+(H)}(\tau^{\prime})>=\frac{1}{z}\int D [\phi_{\alpha}^{*}(\tau),\phi_{\alpha}(\tau)]\phi_{\alpha}(\tau)\phi_{\beta}^{*}(\tau^{\prime}) e^{-S_{0}}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{0}=\sum\limits_{\alpha}\frac{1}{\beta}\sum\limits_{\omega_{n}\phi_{\alpha,i\omega_{n}}}\phi_{\alpha,i\omega_{n}}^{*}(-i\omega_{n}+\epsilon_{\alpha}-\mu)\phi_{\alpha,i\omega_{n}}}
So Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <S_{int}>=\frac{\int\limits_{\phi_{\alpha(\beta)}=\varsigma\phi (0)} D\left[\phi_{\alpha}^{*}(\tau)\phi_{\alpha}(\tau)\right] \frac{1}{\beta^{3}}\sum\limits_{\omega_{n},\Omega_{n},\nu_{n}}\frac{1}{L^{3}}\sum\limits_{k,q,p}V_{q}c^{*}(k,i\omega_{n})c^{*}(p,i\nu_{n})c(p+q,i\nu_{n}+i\Omega_{n})c(k-q,i\omega_{n}-i\Omega_{n}) e^{-\frac{1}{\beta}\sum\limits_{\omega_{n},k}(-i\omega_{n}+\epsilon_{k}-\mu)c^{*}(k,i\omega_{n})c(k,i\omega_{n})}}{Z_{0}}}
and there are two different contraction:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^{*}(p,i\nu_{n})c(p+q,i\nu_{n}+i\Omega_{n}),c^{*}(k,i\omega_{n})c(k-q,i\omega_{n}-i\Omega_{n}) } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q,\Omega_{n}! \rightarrow 0}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^{*}(k,i\omega_{n})c(p+q,i\nu_{n}+i\Omega_{n}),c^{*}(p,i\nu_{n})c(k-q,i\omega_{n}-i\Omega_{n})} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=q+p,\nu_{n}=\omega_{n}-\Omega_{n}}
by using Wick's Theorem Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\int D[\psi^{*},\psi]\xi_{i1}\psi_{i2}...\psi_{in}\psi_{jn}^{*}...\psi_{j2}^{*}\psi_{j1}^{*}e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}}{\int D[\psi^{*}\psi]e^{-\sum\limits_{i,j}\psi_{i}^{*}M_{i,j}\psi_{j}}}=\sum_{p}\xi^{p}M_{ip_{n},j_{n}}^{-1}M_{ip_{n-1},j_{n-1}}^{-1}...M_{ip_{1},j_{1}}^{-1}}
we can get: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <S_{int}>=\frac{1}{\beta^{3}}\sum\limits_{\omega_{n},\nu_{n}}\frac{1}{L^{3}}\sum\limits_{k,p}V_{q=0}\frac{\beta}{-i\omega_{n}+\epsilon_{k}-\nu}\frac{\beta}{-i\nu_{n}+\epsilon_{n}-\nu}-\frac{1}{\beta^{3}}\sum\limits_{\omega_{n},\Omega_{n}}\frac{1}{L^{3}}\sum\limits_{k,q}V_{q=0}\frac{\beta}{-i\omega_{n}+\epsilon_{k}-\nu}\frac{\beta}{-i\omega_{n}+\epsilon_{k-q-\mu}-\Omega_{n}}}
In order to calculate the summations, consider a single Matsubara Frequency Summation,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=\sum\limits_{n}h(\omega_{n})}
After applying Matsubara Frequency Summation, we get: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <S_{int}>_{0}=\beta L^{3}\int\frac{d^{3}k}{(2 \pi)^3}\int\frac{d^{3}p}{(2 \pi)^3}n_{f}(\epsilon_{k})n_{f}(\epsilon_{p})V_{q=0} -\beta L^{3}\int\frac{d^{3}k}{(2 \pi)^3}\int\frac{d^{3}p}{(2 \pi)^3}n_{f}(\epsilon_{k})n_{f}(\epsilon_{p})V_{k-p}}
the former is Hantree term, the later is Fock term.
Matsubara Frequency Summation
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=\sum\limits_{n}h(\omega_{n})} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} is some function and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{n}} may be either bosonic or fermionic.The basic idea behind the standard scheme of evaluating sums of this type is to introduce a complex auxiliary functionFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(z)} that has simple poles at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=i \omega_{n}} . The sum S emerges as the sum of residues obtained by integrating the product Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle gh} along a suitably chosen path in the complex plane. Typical choices of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} include
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(z)= \{_{\frac{\beta}{e^{\beta z}+1}, fermions}^{\frac{\beta}{e^{\beta z}-1}, bosons}}
then produces:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\zeta}{2 \pi i}\oint dz g(z)h(-\pi z)= \zeta \sum\limits_{n} Res(g(z)h(-i z))\mid_{z=i \omega_{n}}=\sum\limits_{n}h(\omega_{n})=S}
Linked cluster theorem
Expand Z we can have all powers of the volume V, but the ground potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=-\frac{1}{\beta}lnZ=-PV} is only depend on V. So in the expansion for Z, all powers of V must be regroup to obtain extensive expansion for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} . The linked cluster theorem concludes that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle lnZ} can be expressed by the sum of all the connected diagrams. Cummulant expansion of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle < e^{-S_{int}}>_{0}} can show the idea of this theorem.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <e^{-S_{int}}>_{0}=e^{-\beta(F-F_{0})}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =1-<S_{int}>_{0}+\frac{1}{2!}<S_{int}^{2}>_{0}+...}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx e^{-<S_{int}>_{0}}+\frac{1}{2}(<S_{int}^{2}>_{0}-<S_{int}>^{2})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z^{n}=e^{n\cdot lnZ}=1+n\cdot lnZ+\sum_{m=2}^{\infty}\frac{(n\cdot lnZ)^{m}}{m!}}
We calculate, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{n\rightarrow 0}\frac{d}{dn}Z^{n}=\lim_{n\rightarrow 0}\frac{d}{dn}(e^{n lnZ)}=lnZ}
Since,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{Z}{Z_{0}}=\frac{1}{Z_{0}}\int_{\Phi_{\alpha}(\beta)=\xi\Phi_{\alpha}(0)}D(\Phi_{\alpha}^{*}(\tau),\Phi_{\alpha}(\tau))e^{-\int_{0}^{\beta}dt(\sum_{\alpha}^{}\Phi_{\alpha}^{*}(\tau)(d_{t}+\varepsilon_{\alpha}-\mu)\Phi_{\alpha}(\tau)-V(\Phi_{\alpha}^{*}(\tau),\Phi_{\alpha}(\tau)))}}
We may write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z^{n}} as a functional integral over n sets of fields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\Phi_{\alpha}^{*\sigma}(\tau),\Phi_{\alpha}^{\sigma}(\tau)\}} , where the index Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} is from 1 to n.
So,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{Z}{Z_{0}}\right)^{n}=\frac{1}{Z_{0}^{n}}\int_{\Phi_{\alpha}^{\sigma}(\beta)=\xi\Phi_{\alpha}^{\sigma}(0)}\prod_{\sigma=1}^{n}D(\Phi_{\alpha}^{*\sigma}(\tau),\Phi_{\alpha}^{\sigma}(\tau))e^{-\int_{0}^{\beta}dt\sum_{\sigma=1}^{n}(\sum_{\alpha}^{}\Phi_{\alpha}^{*\sigma}(\tau)(d_{t}+\varepsilon_{\alpha}-\mu)\Phi_{\alpha}^{\sigma}(\tau)-V(\Phi_{\alpha}^{*\sigma}(\tau),\Phi_{\alpha}^{\sigma}(\tau)))}}
The Feynman rules for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{Z}{Z_{0}}\right)^{n}} are the same as those for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{Z}{Z_{0}}} . It is evident that each connected part of a diagram must carry a single index, which when summed from 1 to n, yields a factor n. Thus, a graph with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{c}} connected parts is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{n_{c}}} and the graphs proportional to n are those with only one connected part, that is the connected graphs. In conclusion, we have got the linked cluster theorem:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F-F_{0}=-\frac{1}{\beta}\sum(all\ connected\ graphs)}
where, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{0}} is the grand potential of the unperturbed system:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{0}=\frac{\xi}{\beta}\sum_{\alpha}ln(1-\xi e^{-\beta(\varepsilon_{\alpha}-\mu)})}
Diagramatic perturbation theory
In this section, we consider the case of a Hamiltonian which has been decomposed into the sum of a one-body operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}} and the residual Hamiltonian V, which in general may contain a one-body interaction as well as many-body interactions, and develop a systematic perturbation expansion in powers of V. The basis will be chosen to diagonalize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}=\sum_{\alpha}\varepsilon_{\alpha}a_{\alpha}^{+}a_{\alpha}} and we will write the normal-ordered many-body part a as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(a_{\alpha}^{+}a_{\beta}^{+}...a_{\gamma}a_{\delta}..)} .
For example for a 3D electron gas in an external magnetic field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H(r,t)} we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\int d^{3}r(\sum_{\sigma}\psi_{\sigma}^{+}(r)(\frac{p^{2}}{2m}-\mu)\psi_{\sigma}(r)-\mu_{B}H(r,t)\psi_{\sigma}^{+}(r)\psi_{\sigma}(r))}
To calculate the average of magnetic momentum, we first calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}(\tau-\tau^{'},r-r^{'})} in imaginary time and then we calculate real time Green's function.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}(\tau-\tau^{'},r-r^{'})=-<T_{\tau}(\psi_{\alpha}^{+}\sigma_{\alpha\beta}^{z}\psi)^{(H)}(\psi_{\gamma}^{+}\sigma_{\gamma\delta}\psi_{\delta})^{(H)}} >
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{1}{Z}\int D[\Phi_{\sigma}^{*}(r,\tau),\Phi_{\sigma}(r,\tau)]\Phi_{\alpha}^{*}(r,\tau),\sigma_{\alpha\beta}^{z}\Phi_{\beta}(r,\tau)\Phi_{\gamma}^{*}(r^{'},\tau^{'})\sigma_{\gamma\delta}^{z}\Phi_{\delta}(r^{'},\tau')e^{-S}}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=\int_{0}^{\beta}d\tau\int d^{3}r\Phi_{\sigma}^{*}(r,\tau)(\frac{\partial}{\partial\tau}+\frac{p^{2}}{2m}-\mu)\Phi_{\sigma}(r,\tau)} .
In general potential we can expand in power series and then like this case we get an integral like Gaussian integral but some powers in front of it. For this case we have a very useful theorem that we like to introduce here.
Now, we calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}(\tau-\tau^{'},r-r^{'})} by using of this theorem. In this case, we have four terms Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\Phi_{\alpha}^{*}(r,\tau),\sigma_{\alpha\beta}^{z}\Phi_{\beta}(r,\tau)\Phi_{\gamma}^{*}(r^{'},\tau^{'})\sigma_{\gamma\delta}^{z}\Phi_{\delta}(r^{'},\tau'))} inside the integral. If we make them in order we will have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{\beta}(r,\tau)\Phi_{\delta}(r^{'},\tau')\Phi_{\gamma}^{*}(r^{'},\tau^{'})\Phi_{\alpha}^{*}(r,\tau)} we can get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}(\tau-\tau^{'},r-r^{'})=\sigma_{\alpha\beta}^{z}\sigma_{\gamma\delta}^{z}(G_{23}G_{14}-G_{13}G_{24})}
Where we used label 1,2,3,4 for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{\beta}(r,\tau),\Phi_{\delta}(r^{'},\tau'),\Phi_{\gamma}^{*}(r^{'},\tau^{'}),\Phi_{\alpha}^{*}(r,\tau)} respectively. We can simplify more because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{23}\leftrightarrow G_{\delta\gamma}(r^{'}-r^{'},\tau^{'}-\tau^{'})} that means Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma,\delta} should be the same and then we get zero for this term.
So
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}(\tau-\tau^{'},r-r^{'})=\sigma_{\alpha\beta}^{z}\sigma_{\gamma\delta}^{z}G_{\beta\gamma}(r-r^{'},\tau-\tau^{'})G_{\delta\alpha}(r-r^{'},\tau-\tau^{'})}
Then we calculate Fourier transform of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{\beta}d\tau e^{i\Omega_{n}\tau}\int d^{3}re^{-iq.r}\overline{D}(\tau,r)=\sigma_{\alpha\beta}^{z}\sigma_{\gamma\delta}^{z}\int_{0}^{\beta}d^{3}re^{-iq.r}\frac{1}{\beta}\sum_{i\omega_{n}}\frac{1}{V}\sum_{k}e^{-i\omega_{n}\tau}e^{ik.r}G_{\beta\gamma}(k,i\omega_{n})\frac{1}{\beta}\times}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i\nu_{n}}\frac{1}{V}\sum_{p}e^{i\nu_{n}\tau}e^{-ip.r}G_{\gamma\delta}(p,i\nu_{n})=\sigma_{\alpha\beta}^{z}\sigma_{\gamma\delta}^{z}\delta_{\beta\gamma}\delta_{\gamma\delta}\frac{1}{\beta}\sum_{i\omega_{n}}\int\frac{d^{3}k}{(2\pi)^{3}}\frac{1}{i\omega_{n}-(\varepsilon_{k}-\mu)}\frac{1}{i\omega_{n}-i\Omega_{n}-(\varepsilon_{k-q}-\mu)}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =2\int\frac{d^{3}k}{(2\pi)^{3}}(-\oint_{c}\frac{dz}{2\pi i}\frac{1}{z-(\varepsilon_{i}-\mu)}\frac{(\frac{1}{e^{\beta z}+1})}{z-i\Omega_{n}-(\varepsilon_{k-q}-\mu)})=2\int\frac{d^{3}k}{(2\pi)^{3}}\frac{n_{f}(\varepsilon_{k}-\mu)-n_{f}(\varepsilon_{k-q}-\mu)}{\varepsilon_{k}-\varepsilon_{k-q}-i\Omega_{n}}}
If we change Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -i\Omega\rightarrow-\Omega-i\eta} we will get the real time Green's function.
For static limit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\Omega=0)and k_{B}T<<\varepsilon_{f}} we can simplify more by using this approximation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{f}(\varepsilon_{k}-\mu)-n_{f}(\varepsilon_{k-q}-\mu)\simeq-\frac{\partial}{\partial\varepsilon}n_{f}(\varepsilon)\mid_{\varepsilon_{k}-\mu}(\varepsilon_{k-q}-\varepsilon_{k})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\mu_{B}S^{z}>=2\mu_{B}^{2}N(\mu)H=\frac{3}{2}\mu_{B}^{2}\frac{\rho}{E_{f}}H}
and for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{B}T>>\varepsilon_{f}} : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\mu_{B}S^{z}>=-2\beta\frac{\rho}{2}} that is Pauli paramagnetic response to the magnetic field.
So, as we saw in the previous part for an operator likeFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <T_{\tau}[a_{\alpha1}(\tau_{1})a_{\alpha2}(\tau_{2})a_{\alpha2^{'}}^{+}(\tau_{2}^{'})a_{\alpha_{1}^{'}}^{+}(\tau_{1}^{'})]>_{0}}
we can write as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\Psi_{\alpha1}(\tau_{1})\Psi_{\alpha2}(\tau_{2})\Psi_{\alpha2^{'}}^{+}(\tau_{2}^{'})\Psi_{\alpha_{1}^{'}}^{+}(\tau_{1}^{'})]>_{0}=G_{\alpha1,\alpha2^{'}}(\tau_{2}-\tau_{2}^{'})G_{\alpha1,\alpha1^{'}}(\tau_{1}-\tau_{1}^{'})+\xi G_{\alpha2,\alpha1^{'}}(\tau_{2}-\tau_{1}^{'})G_{\alpha1,\alpha2^{'}}(\tau_{1}-\tau_{2}^{'})}
So only we need enumerate all the complete sets of contractions contributing to the thermal average of products of the potentioal V. It is convenient to represent this expansion in terms of diagrams. first consider the partition function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z} as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D[\Psi^{*}(\tau),\Psi(\tau)]e^{-S}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=S_{0}+S_{int}} So we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D[\Psi^{*}(\tau),\Psi(\tau)]e^{-S_{0}}(1-S_{int}+\frac{1}{2!}S_{int}^{2}-...)}
Each outgoing line will be connected to an ingoing line with a directed line corresponding to the propagator.
First term Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (S_{int})} gives us Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-1}{2}\int_{0}^{\beta}d\tau\sum_{\alpha\beta\gamma\delta}<\Psi_{\alpha}^{*}(\tau)\Psi_{\beta}^{*}\Psi_{\delta}(\tau)\Psi_{\gamma}(\tau)>_{0}}
The set of all possible ways of connecting interactions with propagators corresponds precisely to the set of all the contractions arising from Wick's theorem. So summation over a complete set of distinct diagrams will faithfully reproduce each of the desired contractions. At order n=1, there are two diagrams corresponding to the two contractions contributing to the integral.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-1}{2}\int_{0}^{\beta}d\tau\sum_{\gamma\delta}G_{\gamma}^{(0)}(0)G_{\delta}^{(0)}(0)V_{\gamma\delta\gamma\delta}=}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-1}{2}\xi\int_{0}^{\beta}d\tau\sum_{\gamma\delta}G_{\gamma}^{(0)}(0)G_{\delta}^{(0)}(0)V_{\delta\gamma\gamma\delta}=}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2!}\frac{1}{4}\frac{-1}{2}\int_{0}^{\beta}d\tau\int_{0}^{\beta}\sum_{\alpha\beta\gamma\delta}\sum_{\alpha^{'},\beta^{'},\gamma^{'},\delta^{'}}V_{\alpha^{'}\beta^{'}\gamma^{'}\delta^{'}}<\Psi_{\alpha}^{*}(\tau)\Psi_{\beta}^{*}(\tau)\Psi_{\delta}^{*}(\tau)\Psi_{\gamma}^{*}(\tau)\Psi_{\alpha^{'}}(\tau^{'})\Psi_{\beta^{'}}(\tau^{'})\Psi_{\delta^{'}}(\tau^{'})\Psi_{\gamma^{'}}(\tau^{'})>_{0}=}
 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +}
Feynman Diagrams
Complete calculations of Green's functions is a rather formidable task. Even the basic imaginary time evolution operator itself is an infinite series to all orders in the interaction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(\vec{r}, \tau)} . One can simply get lost in the dozens of integrals; his physical intuition also doesn't get things any better. Feynman diagrams are both an exact mathematical representation of perturbation theory in infinite order and a powerful pictorial method showing in a unique way the physical content of a given expression.
The introduction of Feynman diagrams to Solid State Physics came naturally in order to give an alternate, and more easy to use, way to apply perturbative concepts beyond lowest orders. Given the so-called Feynman rules, a process can be illustrated in a much more transparent way. This alternate formulation is completely equivalent with the algebraic one. The correspondence with Quantum Field Theory, (QED, QCD and more) where the diagrams were first introduced, is more than obvious. Julian Schwinger once said rather bitterly that “Like the silicon chips of more recent years, the Feynman diagram was bringing computation to the masses”. This will become apparent at the end.
If actually someone wants to compute scattering amplitudes for real physical situations using just Wick's theorem, his job will be cumbersome. Feynman diagrams simplify this task a lot. From a mathematical point of view, they form a consistent framework. Moreover they are completely equivalent with the Wick's theorem approach.
Simple examples
The quantity of interest is a Green's function. The language used more often in QFT is the propagator. More precisely we are interested in the n-th order corrections of it. Of course even from the 2nd order things become slightly complicated as we will see. Let's begin with no interaction at all, just the calculation of the probability of the propagation of a particle from position x to position y, or in a more accurate language the quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle \phi(x)\phi(y) \right \rangle } which as we know is represented by a Green's function, i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(x-y)} . In the language of Feynman diagrams it means that we draw an internal line at x and an external line at y.
The internal line is represented by a leg (line) having an arrow that moves to a vertex (a solid dot) ![]() and the external line by a leg moving from a vertex
and the external line by a leg moving from a vertex ![]() .
.
In order to construct the simplest diagram of all, we connect the two vertices in the only possible way, a line:
and by simplifying things we keep only the in between part
which is nothing else but Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(x-y) } .
1st order correction Let's try now a more complicated vertex, we will demonstrate the 1st order correction to Green's function. Let's suppose that we have 2 fields again Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(x),\phi(y)} , one in position x and another in y. . Hence we have 2 lines as before. But now the vertex we put in between (position z) is this one, we call it vertex Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi^4(z)} :
Now we should connect the two lines, external and internal, with the above vertex in all possible ways. One way is just to connect x with y and ignore the vertex. Of course we take into account the vertex lines and we draw the appropriate (directional in this case) loops between them:
(If there are no arrows, our loops also have no arrows, we will show it next, in 2nd order correction).
Now the other possibility is to connect x with z and z with y. In our case it can be done in 2 ways as far as the internal line is concerned because there are 2 ingoing lines in the vertex, and in other 2 ways for the external lines, total of 4 ways. The lines from the vertex that remain unconnected, form a loop as before. Let's illustrate this, (having in mind that the topology of the following two diagrams is the same though and that in the future they will be represented as one diagram):
Therefore the three above diagrams represent the total average Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle \phi(x)\phi^4(z)\phi(y) \right \rangle } which now can be analyzed in 2 terms that contain the Green's functions, first term for the first unconnected diagram and the 2nd term for the other two connected diagrams:
The simplification in terms of Feynman diagrams is obvious. This is the 1st order correction to the Green function.
2nd order correction
The 2nd order correction contains 2 vertices at z, z' positions, with no arrows now:
We want to compute Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle \phi(x)\phi^4(z')\phi(y) \right \rangle }
. Let's just write the final result, no arrows this time to make it easier. The numbers in front of the diagrams are called combinatorial factors and they are obviously positive integers; they represent the total ways that this particular topology can be realized:
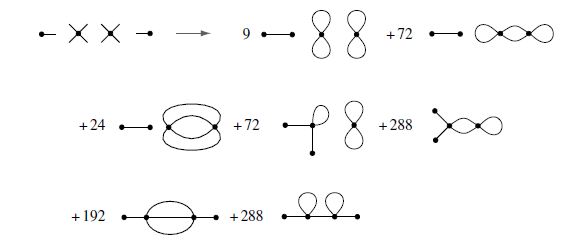
The problem of determining the combinatorics remains highly non-trivial. For example in the next correction, (3rd), the number of terms are (14-1)!!=135135. We will address it later. We will highlight some general remarks of Feynman diagrams and then we will attempt to calculate a more interesting case of interacting fermions.
General remarks
- Feynman diagrams represent the perturbative expansion. In order to be able to compute it we need the rules that relate the objects which consist the graph to analytical expressions. These are called Feynman rules, we will develop them later, for now we can just say that
(i) we attach coordinates to all field lines and all of the vertices
(ii) lines are the representation of Green's functions (propagators or correlation functions)
(iii) multiply the graph by the factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{g^n}{n!}} .
(iv) integrate over all the internal coordinates, special care in loops
(v) switching from coordinate space to momentum representation of the various quantities is possible and sometimes makes things easier.
(vi) To obtain the Green's function we need to add the contributions emanating from the expansion of the denominator of the functional average. We will explicitly show it later.
- The diagrams can be stretched, mirror inverted, twisting, rotating and otherwise deformed; only their topology matters. Also loops that are linked only to external or internal lines, can be removed in order to end up with a so-called "amputated" diagram. A loop linked only to an external / internal line represents a slight perturbation in our incoming particle beam, it's arbitrary.
- We can attach a loop order to any diagram which is the number of inequivalent loops formed by segments of lines that correspond to Green functions.
- When an interaction vertex does not connect to any of the external vertices, we call it vacuum graph. This graph does not correspond to the correction of Green's function in that order. Formally one can see that by expanding the denominator of the correspondent Green's function and by observing the exact cancellation of the vacuum graph's contribution (linked cluster theorem, which is stated and proved above). For example in the 1st order perturbation theory, excluding the arrows for a second, we got these two different topologies:
But the first one is a vacuum graph. Therefore the graph that will eventually contribute to our calculation is only the second one. Pictorially:
Hence in the 2nd order of perturbation theory the diagrams that contribute are the following:
Fermions with pair interactions - The Feynman diagrams treatment
Let's illustrate how we can incorporate FD into a real-life example, system of fermions with pair interactions. The unperturbed Hamiltonian is
while the interaction term is written as
Obviously Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=H_{0}+V}
. will derive the Feynman rules for the diagrammatic expansion in orders of V of the following Green's function
For simplicity we will write
. The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi}
fields are given in Heisenberg representation, we will convert them to Interaction representation. By subscript "0" we mean averages with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^-}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^\beta}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^H_{0}}
. We write for G:
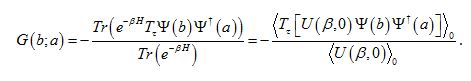
We will need the help of the following expansion, also known from QFT, it's the time-ordering operator expansion:
Now we insert this expansion into the G(b;a) relation above, adjusted to our needs. We get:
As always in these cases we are cautious about the ordering of creation and annihilation operators. The equation for V above forces us to keep creation operators to the left. This restriction can be realized formally in another more clear way. We add in infinitesimal time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta = 0^+} in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi ^+} fields to make sure that the time ordering is right, i.e. the time coordinate in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi ^+} fields is always greater than the time coordinate in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi} fields. of (b;a) we had before denoting all the indices, we switch to "j+" notation as:
Hence the tau-integrals of V in the above large expression can be written in the light of this new notation as
Armed with this machinery we can go back to the big expression for G(b;a) and rewrite it:
The averages are with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}} only. Actually the average of the products of field operators in the numerator is the bare (2n+1)-particle Green's function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_0^{2n+1}(b,1,1,...,n';a,1,1,...,n')} times a factor of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1)^{2n+1}=-1} . Denominator is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_0^{2n}(1,1,...,n';1,1,...,n')} times Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1)^{2n}=1} , hence the overall minus sign is taking care with another one. Using Wick's theorem (which is stated and proved above) for the above Green's functions we write G(b;a) in terms of the determinants containing the bare single particle Green's function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^0(l,j)} . Let's do it:
Derivation of Feynman rules based on G(b;a):
We will derive the Feynman rules for the denominator and then for the numerator. We will see that a cancellation will take place exactly as before in the trivial examples. Here we will see it happening in detail.
(i) lines:
this is equal to the bare single particle Green's function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^0(j_2,j_1)}
. As always in this case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_1}
becomes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_1+\eta}
(ii) interaction lines:
That's equal to the interaction term of the total Hamiltonian, i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{jj'}}
.
(iii) vertices in point j. It's just a dot and it's equal to the sum over the internal variables,
(iv) Then, we draw (2n)! sets of n interaction lines, and
(v) for each of those sets we connect the 2n dots (vertices) with 2n fermion lines. Total number of ways this can be realized is (2n)!.
That would be all if there was no sign change. But there is and it's coming from the determinant's expansion. There will be lines that start from a point j, connecting to other vertices and then come back to j. Hence they form a loop. Loops are very important, especially in QFT, often we treat them in special ways. In our case now, a loop can start from a point and on its way can connect to others or not, but the final destination is always the initial point. Let's illustrate this for 1, 2 and 3 points respectively:
,
,
.
The overall sign will be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1)^F} where F is the number of the fermion loops. Then, all the other diagrams can be constructed by just pair wise interchange of the endpoints of the fermion lines, keeping everything else the same, the determinant sign changes accordingly. Therefore,
(vi) We multiply by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{n!}{(\frac{-1}{2}}^n)(-1)^F} and we add the resulting (2n)! diagrams of order n. Hence for all n there are (2n)! terms of diagrams of order n. After all this the denominator's expansion as far as the Feynman diagrams are concerned, is the following:
plus 1 of course. The first line has 2 terms obviously, the second line contains 24 terms and the third line 720 terms.
For the numerator now, the difference is the additional terms of fermionic fields Ψ(b) and Ψ(a). The dimension of the n'th order determinant goes from 2n to 2n+1 obviously. The first 3 Feynman rules remain the same, the 4th and 5th change slightly:
(iv) We draw (2n+1)! sets of n interacting lines and 2 external vertices at points a, b.
(v) For each set we connect the 2n+2 vertices with 2n+1 fermion lines, one leaving a, one entering b and one entering and leaving each internal vertex j. After all this the numerator's expansion becomes
where the first line contains 6 terms and the second line 120 terms.
A detailed analysis of the combinations and the factors in front of each diagram reveals that the denominator cancels exactly the disconnected diagrams of the numerator, leaving only the connected ones, exactly as before. Pictorially:
Hence we are in a position to give the final Feynman rules for this theory:
(i) lines: .
This is equal to the bare single particle Green's function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^0(j_2,j_1)}
. As always in this case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_1}
becomes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_1+\eta}
.
(ii) interaction lines:
That's equal to the interaction term of the total Hamiltonian as before.
(iii) vertices in point j. It's just a dot and it's equal to the sum over the internal variables, as before.
(iv) At order n we draw all topologically different (and only the connected!) diagrams containing n interaction lines, 2 vertices a and b and 2n+1 fermion lines, one leaves a, one enters b and another one enters and leaves each internal vertex j.
(v) We multiply each diagram by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1)^F} where F is the number of fermion loops.
(vi) We sum over all the topologically different diagrams.
Linear response
In physics we commonly study the macroscopic properties of a many body system by measuring its response to an external perturbation. For example if we want to study the magnetic susceptibility of a material (a macroscopic property given by the equation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_H \equiv \frac{\partial M}{\partial H}} , we could apply a magnetic field (the external probe, H(Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r},\vec{t}} )), and measure the net magnetization (M) of the system. To aid in our understanding of the experimental results it would be useful if we could mathematically perturb our system with this external field and calculate what the system's response is in terms of the expectation values of the observable, which in this case would be the induced magnetization.
There are many other examples of these types of measurements, where we perturb the system with a small localized external force around some point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}} and at some time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} and then measure the response of the system at some later time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t' > t} . For example neutron scattering experiments can probe the local spin density of a system and an applied electric field could determine the electric susceptibility of a material.
To see how an external force perturbs the system we need to consider a many body state ultimately written in the Heisenberg representation so that the time evolution is found in the operators and then use time dependent perturbation to see how the whole system evolves in time. We will now present one derivation of an equation to study the linear response of the system via a response function.
First consider a many body state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi>} , and the time dependant Schrodiger equation
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} i\hbar \frac{\partial}{\partial t}|\Psi(t)> = H(t)|\Psi(t)> \end{align}}
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |\Psi(t)> = T e^{\frac{-i}{\hbar}\int_{t_0}^t \hat H(t^\prime))dt^\prime}|\Psi(t_0)> (2) \end{align}}
where T is the time ordered product, and the time dependent Hamiltonian can be written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat H(t) = \hat H + U(t)\hat O_1} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat H = \hat H_0 +\hat H_{int}} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(t) } is the external perturbation and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat O_1} is the observable that the external perturbation couples to.
The exponential in equation (2) cannot be written as a product of exponentials since in general Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat O_1} does not commute with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat H } . We instead expand the exponential in small t.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} T e^{\frac{-i}{\hbar}\int_{t_0}^t \hat H(t^\prime))dt^\prime} = e^{\frac{-i}{\hbar}(\hat H + U(t)\hat O_1)\Delta t} e^{\frac{-i}{\hbar}(\hat H + U(t-\Delta t)\hat O_1)\Delta t} e^{\frac{-i}{\hbar}(\hat H + U(t-2\Delta t)\hat O_1)\Delta t}... e^{\frac{-i}{\hbar}(\hat H + U(0)\hat O_1)\Delta t} \end{align}}
and then expand each to powers of U
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} = e^{\frac{-i}{\hbar}\hat H \Delta t}( 1-\frac{i}{\hbar}U(t)\hat O_1 \Delta t...)e^{\frac{-i}{\hbar}\hat H \Delta t}( 1-\frac{i}{\hbar}U(t-\Delta t)\hat O_1 \Delta t...)... e^{\frac{-i}{\hbar}\hat H \Delta t}( 1-\frac{i}{\hbar}U(0)\hat O_1 \Delta t...) \end{align}}
which can be rewritten Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} = e^{\frac{-i}{\hbar}\int_{t_0}^t \hat H dt^\prime} -\frac{i}{\hbar}\int_{t_0}^t dt^\prime e^{\frac{-i}{\hbar}\int_{t^\prime}^t \hat H dt^{\prime\prime}}U(t^\prime)\hat O_1 e^{\frac{-i}{\hbar}\int_{t_0}^{t^\prime} \hat H dt^{\prime\prime}}+ ... \end{align}}
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat O_2}
be some observable, so we consider Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\Psi(t)|\hat O_2 |\Psi(t)>}
.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} <\Psi(t)|\hat O_2|\Psi(t)> = \\ <\Psi(t_0)|e^{\frac{i}{\hbar}\hat H(t-t_0)}\hat O_2 e^{\frac{-i}{\hbar}\hat H(t-t_0)}| \Psi(t_0)> \\ - \frac{i}{\hbar}\int_{t_0}^t dt^\prime U(t^\prime)<\Psi(t_o)| e^{\frac{i}{\hbar}\int_{t_0}^t \hat H dt^\prime}\hat O_2 e^{\frac{-i}{\hbar}\int_{t^\prime}^t \hat H dt^\prime\prime}\hat O_1 e^{\frac{-i}{\hbar}\int_{t_0}^{t^\prime}\hat H dt^{\prime\prime}}|\Psi(t_0)>\\ + \frac{i}{\hbar}\int_{t_0}^t dt^\prime U(t^\prime)< \Psi(t_o)| e^{\frac{i}{\hbar}\int_{t_0}^t \hat H dt^\prime}\hat O_1 e^{\frac{i}{\hbar}\int_{t^\prime}^t \hat H dt^{\prime\prime}}\hat O_2 e^{\frac{-i}{\hbar}\int_{t_0}^{t^\prime}\hat \hat H dt^{\prime\prime}}|\Psi(t_0)> \end{align}}
Noting that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\frac{i}{\hbar}\hat H(t-t_0)}\hat O_2 e^{\frac{-i}{\hbar}\hat H(t-t_0)}} is simply the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat O_2} operator in the Heisenburg repersentation, we can simplify the first term above, denoting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\frac{i}{\hbar}\hat H(t-t_0)}\hat O_2 e^{\frac{-i}{\hbar}\hat H(t-t_0)}} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat O_2^H (t)} . We can also combine the second and third term using the commutator between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat O_2^H (t)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat O_1^H (t^\prime)} . Giving us a form for the expectation value for the observable as below.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} <\Psi(t)|\hat O_2|\Psi(t)> = < \Psi^H|\hat O_2^H (t)| \Psi^H> - \frac{i}{\hbar}\int_{t_0}^t dt^\prime U(t^\prime)< \Psi^H|[ \hat O_2^H (t), \hat O_1^H (t^\prime)]| \Psi^H> \end{align}}
If we are just interested in the change to the system, we look at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\Psi(t)|\hat O_2| \Psi(t)> - < \Psi^H|\hat O_2^H (t)| \Psi^Ht>} denoted as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta < \Psi(t)|\hat O_2 | \Psi(t)>} . Finally, for simplicity in calculations, we rewrite the integral as a step functuon Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Theta (t-t^\prime)} , giving us our final equation,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \delta < \Psi(t)|\hat O_2 | \Psi(t)> = - \frac{i}{\hbar}\int_{-\infty}^\infty dt^\prime \Theta (t-t^\prime) U(t^\prime)< \Psi^H|[ \hat O_2^H (t), \hat O_1^H (t^\prime)]| \Psi^H> \end{align}}
For finite temperature, this last expression can be weighted by the boltzman factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{Z}e^{-\beta(E_\alpha -\mu N_\alpha)}} and summed over all states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} to obtain the physical response of the system to an external perturbation.
Following the above derivation we can see that this is equation is the first order correction to the system due to a perturbation from an external force, which is why this is consider "linear response theory". An example of how this equation can be used to study the magnetization of a system and the underlying physics is done below in detail as an example from Dr. Vafek's Fall 2011 Quantum Many Body class.
Example Consider a system of electrons (including spin) that hop between fixed sites with a probability Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -t} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \hat H_0 = -t\sum_{j=1}^n \sum_{\sigma_{\uparrow \downarrow}} (C_{j,\sigma}^\dagger C_{j+1, \sigma} + C_{j+1,\sigma}^\dagger C_{j, \sigma}) \end{align}} and we have a ground state given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} |GS> = \prod_{k=1}^{k_f}( C_{k \uparrow}^\dagger C_{k \downarrow}^\dagger |0>) \end{align}}
Now, if we have an object with spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{s}} at position j, in an external magnetic field. This magnetic field will couple to the spin, and we must include an additional term in our Hamiltonian
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \hat H = \hat H_0 -\mu \sum_{j=1}^n \vec{s}_j \cdot \vec{B}_j(t) \end{align}}
To continue, we have to write the spin operator in terms of creation and annihilation operators. Since, for example </math>C_{j\uparrow}^\dagger|0></math> creates a spin up, we see
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} S_j^z(C_{j\uparrow}^\dagger|0>) = \frac{\hbar}{2}(C_{j\uparrow}^\dagger |0>)\\ S_j^z(C_{j\downarrow}^\dagger |0>) = \frac{-\hbar}{2}(C_{j\downarrow}^\dagger |0>) \end{align}} this results in counting the number of particles with spin up, and weight it by $\frac{\hbar}{2}$ and count the number with spin down, weighted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-\hbar}{2}} giving
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} S_j^z = \frac{\hbar}{2}(C_{j\uparrow}^\dagger C_{j\uparrow}- C_{j\downarrow}^\dagger C_{j\downarrow}) \end{align}} note that for more than one particle, this above, is summed over j. Now, this can be rewritten below (with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} , the pauli matrix.)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} S_j^z= \frac{\hbar}{2} (C_{j\uparrow}^\dagger, C_{j\downarrow}^\dagger) \sigma _z (C_{j\uparrow}, C_{j\downarrow})\\ =\frac{\hbar}{2}C_{j\alpha}^\dagger \sigma_{\alpha \beta}^z C_{j\beta} \end{align}}
Similar arguments can be simply shown for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_j^x} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_j^y} (Note, using einstein summation convention over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} S_j^x =\frac{\hbar}{2}C_{j\alpha}^\dagger \sigma_{\alpha \beta}^x C_{j\beta}\\ S_j^y =\frac{\hbar}{2}C_{j\alpha}^\dagger \sigma_{\alpha \beta}^y C_{j\beta} \end{align}}
so in general we find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \vec{S}_j =\frac{\hbar}{2}C_{j\alpha}^\dagger \vec{\sigma}_{\alpha \beta} C_{j\beta} \end{align}}
and we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \hat H = \hat H_0 - \mu_B \sum_{j=1}^n \vec B_j(t)C_{j\alpha}^\dagger \vec{\sigma}_{\alpha \beta} C_{j\beta} \end{align}}
We are now ready to ask, "What is the induced magnetization at some time t?" Lets assume the magnetic field is in the z direction, and let the brackets <> imply the boltzman thermal average. Therefore what we are asking is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\mu_B C_{i\alpha}^\dagger \sigma_{\alpha \beta}^z C_{i\beta}>(t)}
And so, we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} =\frac{-i}{\hbar}\int_{-\infty}^\infty dt^\prime \Theta(t-t^\prime)<[\mu_B( C_{i\alpha}^\dagger \sigma_{\alpha \beta}^z C_{i\beta})^{(H)}(t), -\sum_{j=1}^n B_j(t^\prime)\mu_B( C_{j\alpha^\prime}^\dagger \sigma_{\alpha^\prime \beta^\prime}^z C_{j\beta^\prime})^{(H)}(t^\prime)]>\\ =\frac{i}{\hbar}\mu_b^2 \sum_{j=1}^n \int_{-\infty}^\infty dt^\prime \Theta(t-t^\prime)B_j(t^\prime)\sum_{\alpha =1}^2 \sum_{\beta = 1}^2 (-1^\alpha)(-1^\beta)<[C_{i\alpha}^\dagger (t) C_{i\alpha}(t), C_{j\beta}^\dagger(t^\prime) C_{j\beta}(t^\prime)]> \end{align}}
note Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C(t)} implies the creation or annhiliation opperators in the heisenberg representation.
We would like to use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_\alpha(t)= e^{\frac{-1}{\hbar}E_\alpha t}C_\alpha} however, we can't becasue our hamiltonian mixes states. We can instead rewrite everything in momentum space, where our hamiltoniam is diagonalized.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} C_{j\alpha}^{(H)}(t) = e^{\frac{i}{\hbar}Ht}C_{j\alpha}e^{\frac{-i}{\hbar}Ht}\\ C_{j\alpha} = \frac{1}{\sqrt{n}}\sum_{p=1}^n e^{i\frac{2\pi}{n}pj}C_\alpha(p) \end{align}}
so now Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} C_{j\alpha}^{(H)}(t)= \frac{1}{\sqrt{n}}\sum_{p=1}^n e^{i\frac{2\pi}{n}pj}e^{\frac{i}{\hbar}Ht}C_\alpha(p)e^{\frac{-i}{\hbar}Ht} \end{align}}
we now have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C(p)} in the heisenburg representation, and in momenttum space the hamiltonian is diagonal so we have the final form
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} C_{j\alpha}^{(H)}(t)= \frac{1}{\sqrt{n}}\sum_{p=1}^n e^{i\frac{2\pi}{n}pj}e^{\frac{-i}{\hbar}E(p)t}C_\alpha(p) \end{align}}
Now we can rewrite in momentum space
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} =\frac{i}{\hbar}\mu_b^2 \sum_{j=1}^n \int_{-\infty}^\infty dt^\prime \Theta(t-t^\prime)B_j(t^\prime)\sum_{\alpha =1}^2 \sum_{\beta = 1}^2 \sum_{p_1 =1}^n \sum_{p_2 =1}^n \sum_{k_1 =1}^n \sum_{k_2 =1}^n \frac{(-1)^{\alpha+\beta}}{n^2}\\ e^{-i\frac{2\pi}{n}p_1i}e^{\frac{i}{\hbar}E(p_1)t}e^{i\frac{2\pi}{n}p_2i}e^{\frac{-i}{\hbar}E(p_2)t}e^{-i\frac{2\pi}{n}k_1j}e^{\frac{i}{\hbar}E(k_1)t^\dagger}e^{i\frac{2\pi}{n}k_2j}e^{\frac{-i}{\hbar}E(k_2)t^\dagger}\\ <[ C_\alpha^\dagger (p_1) C_\alpha (p_2), C_\beta^\dagger(k_1)C_\beta(k_2)]> \end{align}}
Looking closely at the commutator, we clearly note that the only nonzer contribution comes from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = \beta} from this, we can remove the sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} and we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1)^{\alpha +\beta} = (-1)^{2\alpha} = 1} Also, looking at a generic form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [AB-BA]} we see if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_1 =k_2} then we must have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_1 = p_2} however this would give Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle AB =BA} which is zero. The only way to return the original state, is for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_2 = p_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_1 = p_2} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} <[C_\alpha^\dagger (p_1) C_\alpha (p_2), C_\beta^\dagger(k_1)C_\beta(k_2)]>\\ = \delta_{p_2k_1}\delta{p_1k_1}(1-\delta_{k_1k_2})<n| C_\alpha^\dagger (k_2) C_\alpha (k_1)C_\alpha^\dagger (k_1) C_\alpha (k_2)-C_\alpha^\dagger (p_2) C_\alpha (p_1)C_\alpha^\dagger (p_1) C_\alpha (p_2)|n>\\ = \delta_{p_2k_1}\delta{p_1k_1}(1-\delta_{k_1k_2}))<n|n_\alpha(k_2)(1-n_\alpha(k1)) - n_\alpha(p_2)(1-n_\alpha(p_1))|n>\\ =(1-\delta_{k_1k_2})\delta_{p_2k_1}\delta{p_1k_1}<n|n_\alpha(k_2)-n_\alpha(k_1)|n> \end{align}}
this above is for one state, if we take the thermal average, we get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} = (1-\delta_{k_1k_2})\delta_{p_2k_1}\delta{p_1k_1}(f(E(k_2)) - f(E(k_1))) \end{align}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} is the fermi occupation factor
now plugging this back in, we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} < \mu_B C_{j\alpha}^\dagger \sigma_{\alpha \beta}^z C_{j\beta}>(t)\\ = \frac{2i}{\hbar}\mu_b^2 \sum_{l=1}^n \int_{-\infty}^\infty dt^\prime \Theta(t-t^\prime)B_l(t^\prime)\frac{1}{n^2}\sum_{k\neq k^\prime}e^{\frac{i}{\hbar}(E(k)-E(k^\prime))(t-t^\prime)}e^{-i(k-k^\prime)(j-l)}(f(E(k)) - f(E(k^\prime)) \end{align}}
Now we want to do the integral over t', to do this we need to write B(t') in its fourier harmonics and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Theta (t-t')} in terms of it's fourier components:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} B_l (t') = \int_{-\infty}^{\infty} \frac{d\Omega}{2\pi} e^{-i\Omega t'} B_{l,\Omega} \end{align} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \Theta (t-t') = \int_{-\infty}^{\infty} \frac{d\omega'}{2\pi i}\frac{e^{i\omega'(t-t')}}{\omega' - iO^\dagger} \end{align}}
We can continue now and write the induced magnetization as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} < \mu_B C_{j\alpha}^{\dagger} \sigma_{\alpha\beta}^{z} C_{j\beta} > = \frac{2i}{\hbar} \sum_{l=1}^n \frac{ \mu_B^2}{n^2} \sum_{k\neq k'} \int_{-\infty}^{\infty} \frac{d\omega'}{2\pi i}\frac{e^{i\omega't}}{\omega' - iO^\dagger} \int_{-\infty}^{\infty} \frac{d\Omega}{2\pi} B_{l,\Omega} \\ X\int_{-\infty}^{\infty} dt' e^{-i\Omega t'}e^{-i\omega t'} e^{\frac{i}{\hbar}(E_k - E_{k'})(t-t')} \left(e^{i(k-k')(j-l)}\left(f(E_k) - f(E_{k'})\right) \right) \end{align}}
The integral over t' yields: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2\pi) \delta \left( \omega' + \Omega + \frac{E_k - E_{k'}}{\hbar}\right) } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega' = -\Omega - \left( \frac{E_k - E_{k'}}{\hbar}\right) }
Now if we re-write the induced magnetization with the above integral and substituting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega'} as given above, we can write it as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} = \frac{2\mu_B^2}{\hbar} \sum_{l=1}^n \frac{1}{n^2} \sum_{k\neq k'} \int_{-\infty}^{\infty} \frac{d\Omega}{2\pi} B_{l,\Omega} \left( \frac{e^{-i\Omega t}e^{-\frac{i}{\hbar}(E_k - E_{k'})t}}{-\Omega -\left(\frac{E_k - E_{k'}}{\hbar} \right) - iO^\dagger}\right) e^{-i(k-k')(j-l)} e^{\frac{i}{\hbar}(E_k - E_{k'})t} \left(f(E_k) - f(E_{k'})\right) \end{align}}
Once we simplify the equation we can re-write this as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} < \mu_B C_{j\alpha}^{\dagger} \sigma_{\alpha\beta}^{z} C_{j\beta} > = -\frac{2\mu_B^2}{n^2}\sum_{l=1}^n \sum_{k\neq k'} \int_{-\infty}^{\infty} \frac{d\Omega}{2\pi}\frac{e^{-i\Omega t'}e^{e-i(k-k')(j-l)}B_{l,\Omega}}{(E_k - E_{k'}) + \Omega \hbar + iO^\dagger \hbar} \left(f(E_k) - f(E_{k'})\right) \end{align}}
At this point the next step would be to perform the sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} , however we cannot do that unless we specify the magnetic field in terms of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} . To simply the problem even further let's assume that the magnetic field is static, ie not time dependent, and see how the magnetization of the system responds. For example, let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_{l,\Omega} = B_0\delta(\Omega)cos(ql)2\pi} , and plug that into the equation.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} < \mu_B C_{j\alpha}^{\dagger} \sigma_{\alpha\beta}^{z} C_{j\beta} > = -\frac{2\mu_B^2}{n^2} \sum_{l=1}^n \sum_{k\neq k'} B_0 cos(ql)\frac{\left(f(E_k) - f(E_{k'})\right)}{E_k - E_{k'} + i\hbar O^\dagger} e^{-i(k-k')(j-l)} \end{align}}
We can now easily do the sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \sum_{l=1}^n cos(ql) e^{i(k-k')l} = \frac{1}{2} \sum_{l=1}^n (e^{iql} + e^{-iql})e^{i(k-k')l} = \frac{n}{2} \sum_{l=1}^n \left(\delta_{k', k+q} + \delta_{k', k-q}\right). \end{align}}
Plugging this into the magnetization and summing over k' we can now write:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} < \mu_B C_{j\alpha}^{\dagger} \sigma_{\alpha\beta}^{z} C_{j\beta} > = - \frac{2\mu_B^2}{2n} \sum_{k=1}^n B_0 \left( \frac{\left (f(E_k) - f(E_{k+q})\right)}{E_k - E_{k+q} + i\hbar O^\dagger }e^{iqj} + \frac{\left( f(E_k) - f(E_{k-q}) \right)}{E_k - E_{k-q} + i\hbar O^\dagger}e^{-iqj} \right). \end{align}}
To push this example even further lets let q go to zero. In that case the numerator would go to zero and so would the denominator so we need to take the limit of q being small compared to the lattice spacing (which in this example is one) and then we can explore the effect of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\rightarrow 0} .
The expansion of one of the fermi occupation factors is,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(E_{k+q}) = f(E_k + (E_{k+q} - E_k)) \sim f(E_k) + f'(E_k) (E_{k+q} - E_k) + ..... } , so we can write the magnetization as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} < \mu_B C_{j\alpha}^{\dagger} \sigma_{\alpha\beta}^{z} C_{j\beta} > = -\frac{B_0\mu_B^2}{n} \sum_{k=1}^n \left (\frac{-f'(E_k) (E_{k+q} - E_k)}{E_k + E_{k+q} + i\hbar O^\dagger} + \frac{f'(E_k)(E_{k-q} - E_k)}{E_k - E_{k-q} + i\hbar O^\dagger} \right). \end{align}}
We can simplify this equation and then once we take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar O^\dagger}
to zero we can write this as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{2\mu_B^2B_0}{n} \sum_{k=1}^n f'(E_k)}
, which in the limit of n going to infinity will allow us to write the magnetic moment in the z-direction as in one dimension as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} < \mu_B C_{j\alpha}^{\dagger} \sigma_{\alpha\beta}^{z} C_{j\beta} > = <m_j^{(z)}> = 2\mu_B^2 B_0 \int_{0}^{2\pi} \frac{dk}{2\pi} \left(-f'(E_k)\right). \end{align}}
If we are interested in the susceptibility of the system, as we first mentioned then all we need to do is divide by the magnetic field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_0} . To make the calculation easier, it is also helpful to multiply the equation by one in the form of 1 = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty} d\epsilon \delta (\epsilon - E_k)} . Rearranging the order of the integrals allows us to write the susceptibility as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi = 2\mu_B^2 \int_{-\infty}^{\infty}d\epsilon(-f'(\epsilon)) \int_{0}^{2\pi}\frac{dk}{2\pi}\delta( \epsilon - E_k)}
, where we take into account that since we are integrating over a delta function with energy we can re-write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(E_k)}
as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\epsilon)}
. The second integral is by definition the density of states for a single particle without spin in one dimension so we can re-define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty}\frac{dk}{2\pi} \delta(\epsilon - E_k)}
as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\epsilon)}
.
We can also now change the limits of integration for the energy integral since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\epsilon)} goes to infinity at -2Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} and 2Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} which is due to the energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_k = -2tcos(k)} being periodic between -2Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} and 2Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} . Therefore we can write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi = 2\mu_B^2 \int_{-2t}^{2t} d\epsilon (-f'(\epsilon))(N(\epsilon))} .
At this point we cannot further simplify the equation but it would be useful to examine what happens to the susceptibility at different extremes. Note that the fermi occupation factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\epsilon)}
is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (e^\frac{\epsilon - \mu}{k_B T} +1 )^{-1}}
. Let's explore what happens in the limit that temperature goes to zero.
So in the instance when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \rightarrow 0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(\epsilon)} is sharply peaked at the the chemical potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} . Therefore it would be useful to write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\epsilon)} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\mu + (\epsilon - \mu))} and since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\epsilon - \mu)} is a small quantity given that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon \approx \mu} at low temperatures, we can expand about this. Therefore to first order in temperature the susceptibility is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi = 2\mu_B^2 \int_{-2t}^{2t} d\epsilon (-f(\epsilon)) N(\mu) = 2\mu_B^2 N(\mu) (f(-2t) - f(2t))} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(-2t) = 1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(2t) = 0 } .
Therefore the static susceptibility Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi } is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \chi = \frac{<m_j^{(z)}>}{B_0} = 2\mu_B^2 N(\mu). \end{align}}
We have found that as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \rightarrow 0 } we recover susceptibility for Pauli Paramagnetism.
Now if we explore the instance in which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \rightarrow \infty } we can write the fermi occupation factor as, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\epsilon) \approx e^{-(\epsilon - \mu)/k_B T} } and then directly take the derivative with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } , which yields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(\epsilon) \approx \frac{1}{k_B T} f(\epsilon) }
In this limit the equation for the susceptibility is given simply by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi = \frac{2\mu_B^2}{k_B T} \int_{-infty}^{nifty} d\epsilon N(\epsilon)f(\epsilon). } The integral is simply the particle density n and therefore the susceptibility in this case is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \chi = \frac{<m_j^{(z)}>}{B_0} = 2\mu_B^2 \frac{n}{k_BT}. \end{align}}
In this instance we have found as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\rightarrow \infty } we get the Curie-Weiss Law which is paramagnetic but now dependent on temperature.
A Second Derivation
Consider a system defined with a Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}} that we assume is time-independent, and then add an interaction term as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=H_{0}+U(t)O_{1}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O_{1}} is an operator associated to the external field U(t). Then we are looking for the response of the system to this field. This is found by calculating the average of another operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O_{2}} . For example in an external magnetic field first operator could be spin operator and the next operator (which is averaged over to find the system response) is the magnetic moment of the system.
Now, imagine that the system is described not by a pure state at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=t_{0}} , but by a density matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho _{0}} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho _{0}=\frac{1}{Tr e^{-\beta(H_{0}-\mu N)}}\sum_{n}\mid n>e^{-\beta (E_{n}^{0}-\mu N_{n})}<n\mid}
So we can calculate average of any operator by using of this density matrix. For example for operator R we can say: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\hat{R}>=Tr(\hat{\rho _{0}}\hat{R})} If we want to define density operator in later time(t), only we need to use the evolution operator to create that like this: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\rho _{t}}=\frac{1}{Tr e^{-\beta\hat{(H_{0}}-\mu \hat{N})}}\sum_{n}\hat{u}(t,t_{0})\mid n>e^{-\beta (E_{n}^{0}-\mu N_{n})}<n\mid \hat{u}^{-1}(t,t_{0})}
Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\hat{O_{2}}>=Tr(\hat{\rho _{t}}\hat{O_{2}})=\frac{1}{Z}\sum_{n}e^{-\beta (E_{n}^{0}-\mu N_{n})}<n\mid \hat{u}^{-1}(t,t_{0})\hat{O_{2}}\hat{u}(t,t_{0})\mid n>}
Where Z is the partition function that is as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\frac{1}{Tr e^{-\beta\hat{(H_{0}}-\mu \hat{N})}}} . So in the next step we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\hat{O_{2}}>=\frac{1}{Z}Tr( \hat{u}^{-1}(t,t_{0})\hat{O_{2}}\hat{u}(t,t_{0})e^{-\beta (\hat{H_{0}}-\mu \hat{N})})}
In general this result is a complicated, nonlinear f unction of U(t). In linear response theory we are interested in the right-hand side for vanishing small values of U(t). As we know in the Heisenberg picture we can write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial }{\partial t}\hat{u}(t,t_{0})=(H_{0}+U(t)O_{1}))\hat{u}(t,t_{0})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{u}(t,t_{0})=e^{\frac{i}{\hbar}\hat{H_{0}}({t}'-t_{0})}\hat{u}(t,t_{0})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{u}(t,t_{0})=1+\frac{1}{i\hbar}\int_{t_{0}}^{t}d{t}'U({t}')e^{\frac{i}{\hbar}\hat{H_{0}}({t}'-t_{0})}\hat{O_{1}}e^{-\frac{i}{\hbar}\hat{H_{0}}({t}'-t_{0})}+...}
If we substitute this result in the average of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O_{2}} after some simple calculations we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <\hat{O_{2}}>=\frac{1}{Z}Tr(\hat{O_{2}}e^{-\beta (\hat{H_{0}}-\mu \hat{N})}))+\frac{1}{i\hbar}\frac{1}{Z}\int_{-\infty}^{\infty}d{t}'U({t}')Tr([\hat{O}^{(H)}_{2}(t),\hat{O}^{(H)}_{1}(t)]e^{-\beta (\hat{H_{0}}-\mu \hat{N})})\theta (t-{t}')}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{O}^{(H)}_{2}(t)} shows that we work in the Heisenberg picture. First term is related to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{0}} and we usually consider it equal to zero.
Green's Functions
We already have seen that knowing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{i}{\hbar} \theta (t-t') \left\langle \left[ \mathcal{O}^{(H)}_1(t), \mathcal{O}^{(H)}_2(t') \right] \right\rangle } gives us information about physical response of the system to external perturbation. Now, we will introduce n-body Green's function starting with one-body real-time Green's function.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{G} \left( \alpha_1, t_1 | \alpha_1', t_1' \right) = -i \left\langle T \left( a^{(H)}_{\alpha_1} (t_1) {a^{(H)}_{\alpha_1'}}^{\dagger} (t_1') \right) \right\rangle }
where the time-ordering operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T } is defined by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \left( \mathcal{O}_{\alpha_1}(t_1) \mathcal{O}_{\alpha_2}(t_2) \cdots \mathcal{O}_{\alpha_n}(t_n) \right) = \zeta^{P} \mathcal{O}_{\alpha_{p_1}}\left(t_{p_1}\right) \mathcal{O}_{\alpha_{p_2}}\left(t_{p_2}\right) \cdots \mathcal{O}_{\alpha_{p_n}}\left(t_{p_n}\right) }
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P \!} is the permutation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( 1,2,\cdots, n \right) } which orders the times chronologically with the latest time to the left, i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{p_1} > t_{p_2} > \cdots > t_{p_n} } and
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta = \left\{ {\begin{align} + &: \textrm{Bosons} &{}\\ - &: \textrm{Fermions} &{} \end{align} } \right. }
So, if we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{G} \left( \alpha_1, t_1 | \alpha_1', t_1' \right) = -i \theta \left( t_1 - t_1' \right) \left \langle a^{(H)}_{\alpha_1} (t_1) {a^{(H)}_{\alpha_1'}}^{\dagger} (t_1') \right\rangle -i \zeta \theta \left( t_1' - t_1 \right) \left \langle {a^{(H)}_{\alpha_1'}}^{\dagger} (t_1') {a^{(H)}_{\alpha_1}} (t_1) \right\rangle }
where the brackets denote thermal average.
Real-Time Green's functions
The Green's function is defined as the solution of the differential equtation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (z-L)(\mathbf{r}-\mathbf{r}')G(\mathbf{r},\mathbf{r}';z) = \delta(\mathbf{r}-\mathbf{r}') \qquad\qquad (1) }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L(\mathbf{r})} is a linear, time-independent, hermitian differential operator. The Green's function can be rewritten in bra-ket notation as:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (z-L)G(z) = 1 \qquad\qquad (2) \!}
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\mathbf{r},\mathbf{r}';z) = \langle\mathbf{r}|G(z)|\mathbf{r}'\rangle \qquad\qquad (3) }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\mathbf{r}|L|\mathbf{r}'\rangle = \delta(\mathbf{r}-\mathbf{r}')L(\mathbf{r}) \qquad\qquad (4)}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L|\phi_{n}\rangle = \lambda_{n}|\phi_{n}\rangle \qquad\qquad (5)}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\phi_{n}|\phi_{m}\rangle = \delta_{mn} \qquad\qquad (6)}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum|\phi_{n}\rangle\langle\phi_{n}| = 1 \qquad\qquad (7)}
by rearranging (2) we find that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(z) = \frac{1}{z-L} \qquad\qquad (8)}
by multiplying (8) by (7) and using (5), we obtiain
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(z) = \sum_{n}\frac{|\phi_{n}\rangle\langle\phi_{n}|}{z-\lambda_{n}} \qquad\qquad (9) }
From (9), you can see that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(z) \!} is undefined when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z \!} is equal to the eignevalues of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L \!} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{n} \!} .
The Green's function is nothing but a propagator. It is immediately clear when we write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G (\mathbf{r}t,\mathbf{r'}t') = -i\theta (t-t')\langle\mathbf{r} | e^{-i H(t-t')} |\mathbf{r'}\rangle, \qquad\qquad (10) }
which is a solution of the partial differential equation defining the Green's function
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[i\partial_{t} -H_{0}(\mathbf{r})-V(\mathbf{r})\right]G(\mathbf{r},\mathbf{r'};t,t') = \delta(\mathbf{r}-\mathbf{r}')\delta(t-t') \qquad\qquad (11) }
Single-particle Green's functions
Actually, there are many types of single-particle Green's functions. First, the retarded Green's function is defined as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{G}^{R}(\mathbf{r},\sigma, t | \mathbf{r'},\sigma', t' ) = -i\theta(t-t')\left\langle\left[\Psi_\sigma (\mathbf{r}t), \Psi^{\dagger}_{\sigma'}(\mathbf{r'}t') \right]_{-\zeta}\right\rangle \qquad\qquad (1) }
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta = \left\{ {\begin{align} + &: \textrm{Bosons} &{}\\ - &: \textrm{Fermions} &{} \end{align} } \right. }
Second, we can define the so-called greater and lesser Green's functions
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{>}(\mathbf{r}\sigma t,\mathbf{r'}\sigma' t' ) = -i\langle\Psi_\sigma (\mathbf{r}t), \Psi^{\dagger}_{\sigma'}(\mathbf{r'}t')\rangle } [2]
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{<}(\mathbf{r}\sigma t,\mathbf{r'}\sigma' t' ) = -i(\pm1)\langle\Psi_\sigma (\mathbf{r}t), \Psi^{\dagger}_{\sigma'}(\mathbf{r'}t')\rangle } [3]
We see that the retarded Green's function [1] can be written in terms of these two functions as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{R}(\mathbf{r}\sigma t,\mathbf{r'}\sigma' t' ) = \theta(t-t')[G^{>}(\mathbf{r}\sigma t,\mathbf{r'}\sigma' t' )-G^{<}(\mathbf{r}\sigma t,\mathbf{r'}\sigma' t' )] } [4]
Although we call these Green's functions for "single-particle Green's functions", they are truly many-body objects because they describe the propagation of single particles governed by the full many-body Hamiltonian. Thus, the single-particle functions can include all kinds of correlation effects.
Fourier Transform of Green's function for translational-invariant systems
It is natural to choose Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}} -representation for a system with translational invariance.
Since the system is translation invariant G Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\mathbf{r},\mathbf{r'})} can only depend on the position difference Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}-\mathbf{r'}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{R}(\mathbf{r}-\mathbf{r'},\sigma t,\sigma' t)=\frac{1}{V}\sum_{\mathbf{k,k'}} e^{i\mathbf{k}\cdot\mathbf{r}}G^{R}(\mathbf{k}\sigma t, \mathbf{k'}\sigma',t')e^{-i\mathbf{k'}\cdot\mathbf{r'}} } [5]
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{1}{V}\sum_{\mathbf{k,k'}} e^{i\mathbf{k}\cdot(\mathbf{r-r'})}G^{R}(\mathbf{k}\sigma t, \mathbf{k'}\sigma',t')e^{i(\mathbf{k'-k})\cdot\mathbf{r'}} } [6]
However, because the right hand side cannot explicitly dependent on the origin and on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r'} } , it follows that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\mathbf{k,k'}) = \delta_{\mathbf{k,k'}} G(\mathbf{k}) } , allowing us to write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{1}{V}\sum_{\mathbf{k}} e^{i\mathbf{k}\cdot(\mathbf{r-r'})}G^{R}(\mathbf{k}\sigma t, \mathbf{k'}\sigma',t'), } [7]
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{R}(\mathbf{k}\sigma t, \mathbf{k'}\sigma',t') = -i\theta(t-t')\langle[a_{\mathbf{k} \sigma}(t), a_{\mathbf{k} \sigma}^{\dagger}(t)]_{\pm}\rangle } [8]
Free particle Green functions
One of the most important characteristics of the microscopic properties of a system in quantum field theory is the one-particle Green function. It is defined as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\alpha\beta}(x,x^{'})=-i\langle T(\tilde{\psi}_{\alpha}(x)\tilde{\psi}_{\beta}^{+}(x^{'}))\rangle}
We understand by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} (or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'} ) a set of four variables :the coordinates r and the time I; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} are the spin indices.
As we know the one-particle operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F^{1}} may be written in the new representation in the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F^{1}=\int\psi^{+}(\xi)f^{1}\psi(\xi)d\xi} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} is the field operator.A knowledge of the Green function enables us to find the average over the ground state of any one-particle operator.Indeed, we have from
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F^{1}=\pm i\int[\lim_{t^{'}\rightarrow t,r\rightarrow r^{'}}f_{\alpha\beta}^{1}(x)G_{\alpha\beta}(x,x^{'})]d^{3}r}
(the plus (minus) sign for Bose (Fermi) statistics). For instance, the density of the number of particles and the particle flux density are, respectively, equal to
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n(x)=\pm i\lim_{t^{'}\rightarrow t,r\rightarrow r^{'}}G_{\alpha\alpha}(x,x^{'})}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j(x)=\pm\frac{1}{2m} \lim_{t^{'}\rightarrow t,r\rightarrow r^{'}}(\nabla_{r}-\nabla_{r^{'}})G_{\alpha\alpha}(x,x^{'})}
Green's functions originate in the question, "Starting with a particle at site Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |0)} at time 0, what is the amplitude for finding it at site Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \R)} at time f ?." The answer to this question is that the amplitude is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle R \left| G(t)\rangle \right| 0\rangle = \left\langle R\left| e^{\frac{-i\hat{H}t}{\hbar}}\right|0 \right\rangle } .
Two-particle Green's functions
One important type of higher order Green's functions are the correlation functions, which is used in the linear response theory. For example, the response to electromagnetic radiation is determined by the auto correlation function of the charge and densities. Typical correlation functions are
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C(t,t') = -i\theta(t-t')\left\langle[A(t),A(t')]\right\rangle, }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A } is some two particle operator.
"Example-The polarization function of non-interacting electron gas"
We can define the polariation function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi = C_{\rho\rho}} as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\rho\rho}(\mathbf{r}t,\mathbf{r'}t') = -i\theta(t-t')<[\rho_{e}(\mathbf{r},t),\rho_{e}(\mathbf{r'},t')]> }
If the system has translational invariance, it is natural to use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}} -representation.
In momentum space the polarization is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi^{R}(\mathbf{q},t-t') = \int{d\mathbf{r} \chi (\mathbf{r}-\mathbf{r'},t-t')e^{-i\mathbf{q}\cdot(\mathbf{r}-\mathbf{r'})}} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-i\theta(t-t')\int{d\mathbf{r}<[\rho(\mathbf{r},t),\rho(\mathbf{r'},t')]>e^{-i\mathbf{q}\cdot(\mathbf{r}-\mathbf{r'})}} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-i\theta(t-t')\int{d\mathbf{r} \frac{1} {V^{2}} \sum_{\mathbf{q_{1}} \mathbf{q_{2}}}<[\rho(\mathbf{q_{1}},t),\rho(\mathbf{q_{2}},t')]> e^{i\mathbf{q_{1}}\cdot\mathbf{r}+i\mathbf{q_{2}}\cdot\mathbf{r}'} e^{-i\mathbf{q}\cdot(\mathbf{r}-\mathbf{r}')}}, }
Using the delta function,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-i\theta(t-t')\frac{1} {V} \sum_{\mathbf{q_{2}}}<[\rho(\mathbf{q},t),\rho(\mathbf{q_{2}},t')]>e^{i(\mathbf{q_{2}}+\mathbf{q})\cdot\mathbf{r}'} }
Due to the translation-invariance the result do not depend on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}'} thus, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{q_{2}} = -\mathbf{q} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi^{R}(\mathbf{q},t-t') = -i\theta(t-t')e^2 \frac{1} {V} <[\rho(\mathbf{q},t),\rho(-\mathbf{q},t')]>. }
The second quantization representation of the charge operator,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(\mathbf{q}) = \sum_{\mathbf{q}\sigma} c_{\mathbf{k}\sigma}^{\dagger}c_{\mathbf{k}+\mathbf{q}\sigma}. }
For free electrons, the time dependence of the charge operator is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(\mathbf{q},t) = \sum_{\mathbf{q}\sigma} c_{\mathbf{k}\sigma}^{\dagger}c_{\mathbf{k}+\mathbf{q}\sigma} e^{i(\xi_{\mathbf{k}}-\xi_{\mathbf{k}+\mathbf{q}})t}, }
The polarization function
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{0}^{R} (\mathbf{q},t-t') = -i\theta(t-t')e^{2} \frac{1} {V} \sum_{\mathbf{kk'}\sigma \sigma'} <[c_{\mathbf{k}\sigma}^{\dagger}c_{\mathbf{k}+\mathbf{q}\sigma}, c_{\mathbf{k'}\sigma'}^{\dagger}c_{\mathbf{k'}-\mathbf{q'}\sigma'}]> e^{i(\xi_{\mathbf{k}}-\xi_{\mathbf{k}+\mathbf{q}})t} e^{i(\xi_{\mathbf{k'}}-\xi_{\mathbf{k'}-\mathbf{q}})t'} }
the subindex "0" means the free electron approximation. The commutator can be evaluated using the formula,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [c_{\nu}^{\dagger}c_{\mu'},c_{\nu'}^{\dagger}c_{\mu'}] = c_{\nu}^{\dagger}c_{\mu'}\delta_{\mu,\nu'}-c_{\nu'}^{\dagger}c_{\mu}\delta_{\nu',\mu'},}
and we find
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{0}^{R}(\mathbf{q},t-t') = -i\theta(t-t')e^2 \frac{1} {V} \sum_{\mathbf{k}\sigma} [n_{F}(\xi_{\mathbf{k}})-n_{F}(\xi_\mathbf{k}+\mathbf{q})]e^{i(\xi_{\mathbf{k}}-\xi_{\mathbf{k}+\mathbf{q}})(t-t')}, }
because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <c_{k}^{\dagger}c_{k}> = n_{F}(\xi_{k})} .
In the frequency space, we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_{0}^{R}(\mathbf{q},\omega) = -i\int{dt e^{i\omega t} \frac{1} {V} \sum_{\mathbf{k}\sigma}[n_{F}(\xi_{\mathbf{k}})-n_{F}(\xi_{\mathbf{k}+\mathbf{q}})]e^{i(\xi_{\mathbf{k}}-\xi_{\mathbf{k+q}})(t-t')}e^{\eta(t-t')}} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1} {V} \sum_{\mathbf{k}\sigma} \frac{n_{F}(\xi_{\mathbf{k}}) - n_{F}(\xi_{\mathbf{k}+\mathbf{q}})} {\xi_{\mathbf{k}}-\xi_{\mathbf{k+q}}+\omega+i\eta} }
This function is known as the Lindhard function, we can solve it approximately when temperature and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{q}} is very small using the way we did in class.
Spectral Representation of the Two-Point Green function
The spectral representation of the Green's function provides an intuitive pictures. It's obtained by inserting a complete set of states into
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <T(\partial_{i}u_{i}(\overrightarrow{x}, t)u_{j}(0,0))>}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \theta (t)<\partial_{i}u_{i}(\overrightarrow{x}, t)\partial_{j}u_{j}(0,0)> +\theta (-t)<\partial_{j}u_{j}(0,0)\partial_{i}u_{i}(\overrightarrow{x}, t)>}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\theta (t)\sum_i <\partial_{i}u_{i}(\overrightarrow{x}, t)|i><i|\partial_{j}u_{j}(0,0)>+\theta (-t)\sum_i <\partial_{j}u_{j}(0,0)|i><i|\partial_{i}u_{i}(\overrightarrow{x}, t)>}
where T is time-ordered operator and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } is unit step function.
By translational invariance,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <0|\partial_{i}u_{i}|i> = e^{i\overrightarrow{p}\cdot\overrightarrow{x}}-i\omega_{i}t<0|\partial_{i}u_{i}(0,0)|i> }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{p}_{i} } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{i}} are the momentum and energy of the state |i>.
Thus, we can write the Green's function
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <T(\partial_{i}u_{i}(\overrightarrow{x}, t)u_{j}(0,0))> =\sum _i |<i|\partial_{j}u_{j}(0,0)|0>|^{2}(\theta(t)e^{i(\overrightarrow p_{i}\cdot \overrightarrow x_{i})-\omega_it}+\theta(-t)e^{-i(\overrightarrow p_{i}\cdot \overrightarrow x_{i})-\omega_it}) }
By multiplying Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d^{3}PdE[\delta(P-p_{i})\delta(\omega_{i}-E) ]=1}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\int d^{3} PdE [\sum_i |<i|\partial_{j}u_{j}(0,0)|0>|^{2}\delta(\overrightarrow{P} -\overrightarrow{p_{i}})\delta(\omega_{i}-E)]\times (\theta(t) e^{i(\overrightarrow{P}\cdot \overrightarrow{x}-Et)} )+(\theta(-t) e^{-i(\overrightarrow{P}\cdot \overrightarrow{x}-Et)} )}
Here we can define the spectral function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\overrightarrow{P},E)} , so
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \equiv \int d^{3}\overrightarrow{P} dE |P|^2 A(\overrightarrow{P},E)(\theta(t) e^{i(\overrightarrow{P}\cdot \overrightarrow{x}-Et)} )+(\theta(-t) e^{-i(\overrightarrow{P}\cdot \overrightarrow{x}-Et)} ) }
Let's take the Fourier transform of time, then Green's function is as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\overrightarrow{x},\omega) = \int dt \int d^{3}\overrightarrow{P}dE |P|^{2}A(\overrightarrow{P},E)(\theta(t) e^{i(\overrightarrow{P}\cdot \overrightarrow{x}+(\omega-E+i\delta)t)} )+(\theta(-t) e^{-i(i(\overrightarrow{P}\cdot \overrightarrow{x}+(\omega+E-i\delta)t} ) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \int dt \int d^{3}\overrightarrow{P}dE |P|^{2}A(\overrightarrow{P},E)(\theta(t) e^{i(\omega-E)t-\delta t}e^{i\overrightarrow{P}\cdot \overrightarrow{x}}(\theta(-t) e^{i(\omega+E)t+\delta t}e^{-i\overrightarrow{P}\cdot \overrightarrow{x}}) }
After some arrangements
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\overrightarrow{p},\omega)=\int dE i |p|^{2}(\frac{A(\overrightarrow{p},E)}{\omega-E+i\delta}-\frac{A(-\overrightarrow{p},E)}{\omega+E-i\delta}) }
If the system has parity invariance, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\overrightarrow{p},E) = A(-\overrightarrow{p},E), } so,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\overrightarrow{p},\omega)=\int dE i |p|^{2} \frac{2EA(\overrightarrow{p},E)}{\omega^{2}-E^{2}+i\delta} }
Example-Phonon
If the phonons are non-interacting, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\overrightarrow{p},E) = \delta(E^{2}-\omega_{p}^{2})} , and we recover the free-phonon two-point function.
We can split the sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} into the vacuum state, the one-phonon states, and all other states.
Let's assume that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <0|u_{i}(\overrightarrow{x}_{1}, t_{1})|0> = 0}
and consider one-phonon state with momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{p}} . Then, we will write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |p|^{2}Z = |<0|\partial_{i}u_{i}(0,0)|\overrightarrow{p}>|^{2} } If the system has rotational and Galilean invariances, the left-hand-side is independent of the direction of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{p}} .
Then the spectral function can be broken into two. one is carrying weight Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z} , which looks like a non-interacting phonon, another is incoherent weight
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\overrightarrow{p},E) = Z\delta(E^{2}-\omega_{p}^{2})+A_{inc}(\overrightarrow{p},E) }
The physical meaning is that the phonon propagates as a free phonon with probability Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z} from the first term and as a multi-phonon state of energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} with probability Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_{inc}(\overrightarrow{p},E).}
Thermal(imaginary-time) Green's function
Now, We define Thermal(imaginary-time) Green's function:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{(n)}(\alpha_{1},\tau_{1},...,\alpha_{n},\tau_{n}\mid\alpha_{1}^{'},\tau_{1}^{'},...,\alpha_{n}^{'},\tau_{n}^{'}) = \left\langle T_{\tau}\left[a_{\alpha_{1}}^{(H)}(\tau_{1}).....a_{\alpha_{n}}^{(H)}(\tau_{n}){a_{\alpha_{n}^{'}}^{(H)}}^{\dagger}(\tau_{n}^{'}).....{a_{\alpha_{1}^{'}}^{(H)}}^{\dagger}(\tau_{1}^{'})\right]\right\rangle, }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {a_{\alpha^{'}}^{(H)}}^{\dagger}(\tau^{'})\equiv e^{\tau(H-\mu N)}{a_{\alpha}}^{\dagger}e^{-\tau(H-\mu N)}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\alpha^{'}}^{(H)}(\tau^{'})\equiv e^{\tau(H-\mu N)}a_{\alpha}e^{-\tau(H-\mu N)}} , so that these operators are not Hermitian because they are not conjugate of each other. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{\tau} \!} is the time ordering operator and it is defined as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{\tau}\left[O_{\alpha_{1}}^{(\tau_{1})}O_{\alpha_{2}}^{(\tau_{2})}....O_{\alpha_{n}}^{(\tau_{n})}\right] = \zeta^{p}O_{\alpha_{p_1}}(\tau_{p_1})O_{\alpha_{p_2}}(\tau_{p_2})....O_{\alpha_{p_n}}(\tau_{p_n})}
For example for two operators:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{\tau}[a_{\alpha}^{(H)}(\tau){a_{\beta}^{(H)}}^{\dagger}(\tau^{'})] = {a_{\alpha}^{(H)}}^{\dagger}(\tau)a_{\beta}^{(H)}(\tau^{'})} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau > \tau^{'} \!} or it equals to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm a_{\alpha}^{(H)}(\tau^{'})a_{\beta}^{(H)^{\dagger}}(\tau)} so that the upper sign is for Bosons and the lower sign is for Fermions.
So we can write the Green's function as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{Z}Tr\left[e^{-\beta(H-\mu N)}\zeta^{p} \tilde{a}_{\alpha_{p1}}^{(H)}(\tau_{p_1}) \tilde{a}_{\alpha_{p_2}}^{(H)}....\tilde{a}_{\alpha_{p_{2n}}}^{(H)}(\tau_{p_{2n}})\right],}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p \!} is the permutation which gives Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{p_1}>\tau_{p_2}>....>\tau_{p_{2n}}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{a}_{j}=a_{j}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\tilde{a}_{j+n}}^{\dagger}=a_{j}^{\dagger}} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=1,...,n. \!} Then
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{(n)}\left(\alpha_{1},\tau_{1},...,\alpha_{n},\tau_{n}\mid\alpha_{1}^{'},\tau_{1}^{'},...,\alpha_{n}^{'},\tau_{n}^{'}\right)=\frac{\zeta^{p}}{Z}\textrm{Tr}\left[e^{-\beta(H-\mu N)}e^{\tau_{p1}(H-\mu N)}\tilde{a}_{\alpha_{p1}}e^{-\tau_{p1}(H-\mu N)}...\right] }
If again slice up all exponential terms, we will have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\zeta^{p}}{Z}\textrm{Tr}\left[e^{-\int_{\tau_{p_1}}^{\beta}d\tau^{'}(H-\mu N)}\tilde{a}_{\alpha_{p_1}}e^{-\int_{\tau_{p_2}}^{\tau_{p_1}}d\tau^{'}(H-\mu N)}\tilde{a}_{\alpha_{p_2}}...e^{-\int_{0}^{\tau_{p_{2n}}}d\tau^{'}}\right] = \frac{\zeta^{p}}{Z}\int \mathcal{D} \left( \Phi_{\alpha}^{*}(\tau),\Phi_{\alpha}(\tau)\right) e^{-\int_{0}^{\beta}d\tau \mathcal{L}(\tau)}\tilde{\Phi}_{\alpha_{p_1}}(\tau_{p_1})\tilde{\Phi}_{\alpha_{p_2}}(\tau_{p_2})....\tilde{\Phi}_{\alpha_{p_{2n}}}(\tau_{p_{2n}}), }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L}(\tau) = \sum_{\alpha}\left({\Phi(\tau)}^{*}\left(\frac{\partial}{\partial\tau} -\mu \right)\Phi_{\alpha}(\tau) + \mathcal{H} \left( \Phi(\tau)^{*}, \Phi(\tau) \right)\right)}
Let's calculate the partition function of free bosons/fermions:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}=\sum_{\alpha}\varepsilon_{\alpha}a_{\alpha}^{\dagger}a_{\alpha}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L}(\tau)=\sum_{\alpha}\left[ {\Phi(\tau)}^{*}\left(\frac{\partial}{\partial\tau}+\varepsilon_{\alpha}-\mu\right)\Phi_{\alpha}(\tau) \right]}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{\beta}d\tau \mathcal{L}(\tau) = \sum_{\alpha}\left(\sum_{k=2}^{m}\Phi_{\alpha,k}^{*}\left(\Phi_{\alpha,k}-\Phi_{\alpha,k-1}+\frac{\beta}{m}(\varepsilon_{\alpha}-\mu)\Phi_{\alpha,k-1}\right) +\Phi_{\alpha,1}^{*}\left(\Phi_{\alpha,1}-\zeta\Phi_{\alpha,m}+\frac{\beta}{m}(\varepsilon_{\alpha}-\mu)\zeta\Phi_{\alpha,m}\right)\right)}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\lim_{m\rightarrow\infty}\prod_{\alpha}\left(\int\prod_{k=1}^{m}\frac{d\Phi_{k}^{*}d\Phi_{k}}{N}e^{-\Phi_{i}^{*}S_{ij}^{(\alpha)}\Phi_{j}}\right),}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{ij}^{(\alpha)}=\left(\begin{array}{ccccc} 1 & 0 & ... & ... & -\zeta\lambda\\ -\lambda & 1 & 0 & ... & 0\\ 0 & -\lambda & 1 & ... & 0\\ ... & ... & -\lambda & ... & ...\\ ... & ... & ... & -\lambda & 1\end{array}\right)_{m\times m} } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=1-\frac{\beta}{m}(\varepsilon_{\alpha}-\mu).}
So we can calculate the partition function:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\lim_{m\rightarrow\infty}\prod_{\alpha}\left(\textrm{Det}\left( S_{ij}^{(\alpha)}\right)\right)^{-\zeta} = \prod_{\alpha} \lim_{m\rightarrow\infty}\left(1-\zeta\lambda^{m}\right)^{-\zeta} = \prod_{\alpha} \left(1-\zeta e^{-\beta(\varepsilon_{\alpha}-\mu)}\right)^{\zeta}}
Therefore,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\begin{cases} \begin{array}{ll} \prod_{\alpha}\frac{1}{1-e^{-\beta(\varepsilon_{\alpha}-\mu)}} & \textrm{: \;\; Bosons} \\ \prod_{\alpha}\left(1+e^{-\beta(\varepsilon_{\alpha}-\mu)}\right) & \textrm{: \;\; Fermions} \end{array}\end{cases} }
Moreover, we can get the same result if we work in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k} \!} -space and use the Fourier transformation for functions:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{\alpha}(\tau)=\frac{1}{\beta}\sum_{\omega_n}e^{-i\omega_{n}\tau}\Phi_{\alpha,i\omega_{n}}} ,
where we use the Matsubara frequencies for bosons, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{n}=\frac{2n\pi}{\beta}} , and for fermions, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{n}=\frac{(2n+1)\pi}{\beta}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=0,\pm1,\pm2,....}
Example: calculation of thermal Green's function for two operators
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle T_{\tau}a_{\alpha}^{(H)}(\tau) {a^{\dagger}}^{(H)}(\tau') \right\rangle \equiv \mathcal{G}_{\alpha \beta} \left( \tau, \tau' \right) = \frac{1}{Z}\int_{\Phi_{\alpha}(\beta) = \zeta \Phi_{\alpha}(0)} \mathcal{D}\left(\Phi_{\alpha}^{*}(\tau),\Phi_{\alpha}(\tau)\right)\Phi_{\alpha}(\tau)\Phi_{\beta}^{*}(\tau^{'})e^{-S},}
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{ccl} S &=& \displaystyle \int_{0}^{\beta} d \tau \mathcal{L}_0 \\ {}&=& \displaystyle \int_{0}^{\beta} d \tau \sum_{\alpha} \frac{1}{\beta^2} \sum_{\omega_n} \sum_{\omega_{n}'} e^{i\omega_n\tau} \Phi^{*}_{\alpha,i\omega_n} \left( \frac{\partial}{\partial \tau} + \varepsilon_{\alpha} - \mu \right) e^{-i\omega_n'\tau} \Phi_{\alpha,i\omega_n'}\\ {}&=& \displaystyle \int_{0}^{\beta} d \tau \sum_{\alpha} \frac{1}{\beta^2} \sum_{\omega_n} \sum_{\omega_{n}'} e^{i\omega_n\tau} \Phi^{*}_{\alpha,i\omega_n} \left( -i\omega_n' + \varepsilon_{\alpha} - \mu \right) e^{-i\omega_n'\tau} \Phi_{\alpha,i\omega_n'}\\ {}&{}& \leftarrow \displaystyle \int_{0}^{\beta} d \tau e^{i\left( \omega_n - \omega_n' \right) \tau} = \frac{1}{i\left(\omega_n - \omega_n'\right)} \left( e^{i\left( \omega_n - \omega_n' \right) \beta} -1 \right) = \beta \delta_{\omega_n, \omega_n'} \\ {}&=& \displaystyle \frac{1}{\beta} \sum_{\alpha}\sum_{\omega_{n}}\Phi_{\alpha,i\omega_{n}}^{*}(-i\omega_{n}+\varepsilon_{\alpha}-\mu)\Phi_{\alpha,i\omega_{n}} \end{array} } .
If we use the Fourier transformations, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{\alpha}(\tau)=\frac{1}{\beta}\sum_{\omega_n}e^{-i\omega_{n}\tau}\Phi_{\alpha,i\omega_{n}}} , so we will have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{Z}\int \mathcal{D}\left(\Phi_{\alpha}^{*}(i\omega_{n}),\Phi_{\alpha}(i\omega_{n}')\right) \frac{1}{\beta^{2}}\sum_{\omega_{n},\omega_{n}'}e^{-i\omega_{n}\tau}e^{i\omega_{n}\tau^{'}} \Phi_{\alpha,i\omega_{n}}\Phi_{\beta,i\omega_{n}'}^{*}e^{-\frac{1}{\beta} \sum_{\alpha}\sum_{\omega_{n}}\Phi_{\alpha,i\omega_{n}}^{*}(-i\omega_{n}+\varepsilon_{\alpha}-\mu)\Phi_{\alpha,i\omega_{n}}} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{\partial}{\partial J_{\alpha,i\omega_{n}}^{*}}\zeta\frac{\partial}{\partial J_{\beta,i\nu_{n}}}\frac{1}{Z}\int D[\Phi_{\alpha}^{*}(i\omega_{n}),\Phi_{\alpha}(i\nu_{n})]e^{-S}e^{J_{\alpha,i\omega_{n}}^{*}\Phi_{\alpha,i\omega_{n}}}e^{\Phi_{\beta,i\nu_{n}}^{*}J_{\beta,i\nu_{n}}}\mid_{J=J^{*}=0}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{\partial}{\partial J_{\alpha,i\omega_{n}}^{*}}\zeta\frac{\partial}{\partial J_{\beta,i\nu_{n}}}\frac{(DetL_{\alpha})^{-\zeta}}{(DetL_{\alpha})^{-\zeta}}e^{J_{\alpha,i\omega_{n}}^{*}(\frac{1}{L})J)\alpha,i\omega_{n}}\mid_{J=J^{*}=0}=\frac{\partial}{\partial J_{\alpha,i\omega_{n}}^{*}}J_{\beta,i\nu_{n}}^{*}\frac{1}{L_{\alpha}}e^{J_{\alpha,i\omega_{n}}^{*}(\frac{1}{L})J_{\alpha,i\omega_{n}}}\mid_{J=J^{*}=0}=\delta_{\alpha,\beta}\delta_{\omega_{n,\nu_{n}}}\frac{1}{L_{\alpha}}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\delta_{\alpha,\beta}\delta_{\omega_{n,\nu_{n}}}\frac{\beta}{-i\omega_{n}+\varepsilon_{\alpha}-\mu}}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{\alpha}=\frac{1}{\beta}(-i\omega_{n}+\varepsilon_{\alpha}-\mu)} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <T_{\tau}a_{\alpha}^{(H)}(\tau)a_{\beta}^{+^{(H)}}(\tau^{'})>=\delta_{\alpha\beta}\frac{1}{\beta}\sum_{i\omega_{n}}e^{-i\omega_{n}(\tau-\tau^{'})}\frac{1}{-i\omega_{n}+\varepsilon_{\alpha}-\mu}}
We check this result for two different cases:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a)\tau\leq\tau^{'} : \frac{1}{\beta}\sum_{i\omega_{n}}\frac{e^{-i\omega_{n}(\tau-\tau^{'})}}{i\omega_{n}-(\varepsilon_{\alpha}-\mu)}=\oint\frac{dz}{2\pi i}\frac{e^{-z(\tau-\tau^{'})}}{z-(\varepsilon_{\alpha}-\mu)}\frac{-1}{e^{\beta z}+1}=\frac{e^{-(\varepsilon_{\alpha}-\mu)(\tau-\tau^{'})}}{e^{\beta(\varepsilon_{\alpha}-\mu)}+1}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b)\tau>\tau^{'} : \frac{1}{\beta}\sum_{i\omega_{n}}\frac{e^{-i\omega_{n}(\tau-\tau^{'})}}{i\omega_{n}-(\varepsilon_{\alpha}-\mu)}=\oint\frac{dz}{2\pi i}\frac{e^{-z(\tau-\tau^{'})}}{z-(\varepsilon_{\alpha}-\mu)}\frac{1}{e^{-\beta z}+1}=\frac{-e^{-(\varepsilon_{\alpha}-\mu)(\tau-\tau^{'})}}{e^{-\beta(\varepsilon_{\alpha}-\mu)}+1}}
So in general we have :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\beta}\sum_{i\omega_{n}}\frac{e^{-i\omega_{n}(\tau-\tau^{'})}}{i\omega_{n}-(\varepsilon_{\alpha}-\mu)}=\Theta(\tau^{'}-\tau+\eta)\frac{e^{-(\varepsilon_{\alpha}-\mu)(\tau-\tau^{'})}}{e^{\beta(\varepsilon_{\alpha}-\mu)}+1}-\Theta(\tau^{'}-\tau-\eta)\frac{e^{-(\varepsilon_{\alpha}-\mu)(\tau-\tau^{'})}}{e^{-\beta(\varepsilon_{\alpha}-\mu)}+1}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =e^{-(\tau-\tau^{'})(\varepsilon_{\alpha}-\mu)}([n(\varepsilon_{\alpha}-\mu)\Theta(\tau^{'}-\tau+\mu)+(n_{f}(\varepsilon_{\alpha}-\mu)-1)\Theta(\tau-\tau^{'}-\eta)]}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <T_{\tau}a_{\alpha}^{(H)}(\tau)a_{\beta}^{+^{(H)}}(\tau^{'})>=\delta_{\alpha\beta}e^{-(\tau-\tau^{'})(\varepsilon_{\alpha}-\mu)}([\mp n(\varepsilon_{\alpha}-\mu)\Theta(\tau^{'}-\tau+\mu)+(1\mp n_{f}(\varepsilon_{\alpha}-\mu))\Theta(\tau-\tau^{'}-\eta)]}
Where the upper sign is for fermions and the lower sign is for bosons.
We may obtain this directly as an inverse ofFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial\tau}+\varepsilon_{\alpha}-\eta} by solving
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\frac{\partial}{\partial\tau}+\varepsilon_{\alpha}-\eta)G(\alpha\tau,\alpha\tau^{'})=\delta(\tau-\tau^{'})}
subject to the bounding condition Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\alpha\beta,\alpha\tau^{'})=\zeta G(\alpha0,\alpha\tau^{'})} .
The Green function of the phonons is usually denoted by D. The definition of this function is similar to the previous one as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{12}^{R}(t-t^{'})=-\frac{i}{\hbar}\Theta(t-t^{'})\left\langle \mathcal{O}_{2}^{(H)}(t),\mathcal{O}_{1}^{(H)}(t^{'})] \right\rangle} for real time,where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle O_{2}^{(H)}(t)=e^{\frac{i}{\hbar}H_{0}(t-t_{0})}O_{2}e^{-\frac{i}{\hbar}H_{0}(t-t_{0})}} .
and for imaginary time is as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D_{12}}(\tau-\tau^{'}) = 1 \left\langle T_{\tau} \mathcal{O}_{2}^{(H)}(\tau),\mathcal{O}_{1}^{(H)}(\tau^{'}) \right\rangle } where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{O}_{2}^{(H)}(\tau)=e^{\tau(H_{0}-\mu N)}\mathcal{O}_{2}e^{-\tau(H_{0}-\mu N)}} .
Now we try to connect these two different Green's function to each other. First we start with real time
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\hbar}{i}D_{12}^{R}(t-t^{'})\Theta(t-t^{'})=\frac{1}{Z}Tr[e^{-\beta(H_{0}-\mu N0}(e^{\frac{i}{\hbar}H_{0}(t-t_{0})}O_{2}e^{-\frac{i}{\hbar}H_{0}(t-t_{0})}e^{\frac{i}{\hbar}H_{0}(t^{'}-t_{0})}O_{1}e^{-\frac{i}{\hbar}H_{0}(t^{'}-t_{0})}-}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\frac{i}{\hbar}H_{0}(t^{'}-t_{0})}O_{1}e^{-\frac{i}{\hbar}H_{0}(t^{'}-t_{0})}e^{\frac{i}{\hbar}H_{0}(t-t_{0})}O_{2}e^{-\frac{i}{\hbar}H_{0}(t-t_{0})}]}
In the eigenstate basis we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{1}{Z}\sum_{n}e^{-\beta(E_{n}-\mu N)}(e^{\frac{i}{\hbar}E_{n}(t-t^{'})}<n\mid O_{2}e^{-\frac{i}{\hbar}H_{0}(t-t^{'})}O_{1}\mid n>....)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{1}{Z}\sum_{n,m}e^{-\beta(E_{n}-\mu N)}(e^{\frac{i}{\hbar}(E_{n}-E_{m})(\tau-\tau^{'})}<n\mid O_{2}\mid m><m\mid O_{1}\mid n>-e^{\frac{i}{\hbar}(E_{m}-E_{n})(\tau-\tau^{'})}<m\mid O_{2}\mid n><n\mid O_{1}\mid m>}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{1}{Z}\sum_{n,m}(e^{-\beta(E_{n}-\mu N)}-e^{-\beta(E_{m}-\mu N)})e^{\frac{i}{\hbar}(E_{n}-E_{m})(t-t^{'})}<n\mid O_{2}\mid m><m\mid O_{1}\mid n>}
Then we use the Fourier transformation for this result Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{12}^{R}(\Omega)=\int_{-\infty}^{+\infty}dte^{i\Omega t}D_{12}^{R}(t)} and also a definition for Teta function as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Theta(t)=\frac{1}{2\pi i}\int_{-\infty}^{+\infty}d\nu\frac{e^{i\nu t}}{\nu-i\eta}} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{12}^{R}(\Omega)=\int_{-\infty}^{+\infty}\frac{d\nu}{2\pi i}\int_{-\infty}^{+\infty}dte^{i\Omega t}e^{i\nu t}(-\frac{i}{\hbar})\frac{1}{\nu-i\eta}\frac{1}{Z}\sum_{n,m}(e^{-\beta(E_{n}-\mu N)}-e^{-\beta(E_{m}-\mu N)})e^{\frac{i}{\hbar}(E_{n}-E_{m})(t-t^{'})}<n\mid O_{2}\mid m>\times}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle m \left| O_{1} \right| n \right\rangle = - \frac{i}{\hbar}\frac{1}{Z}\sum_{n,m}\frac{1}{2\pi i}\frac{2\pi}{-\Omega-\frac{E_{n}E_{m}}{\hbar}-i\eta} \left( e^{-\beta(E_{n}-\mu N)}-e^{-\beta(E_{m}-\mu N)}\right) \left\langle n \left| O_{2} \right| m \right\rangle \left\langle m \left| O_{1} \right| n \right\rangle }
And now we calculate the imaginary time
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}_{12}(\tau)=-<O_{2}^{(H)}(\tau)O_{1}^{(H)}(0)>=\frac{-1}{Z}Tr[e^{-\beta(H_{0}-\mu N)}e^{\tau(H_{0}-\mu N)}O_{2}e^{-\tau(H_{0}-\mu N)}O_{1}]}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{1}{Z}\sum_{n,m}e^{-\beta(E_{n}-\mu N)}e^{\tau(E_{n}-\mu N)} \left\langle n \left| O_{2} \right| m \right\rangle e^{-\tau(E_{m}-\mu N)} \left\langle m \left| O_{1} \right| n \right\rangle }
If we again go to the Fourier space, we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}_{12}^{'}(i\Omega_{n})=\int_{0}^{\beta}d\tau e^{i\Omega_{n}\tau}\overline{D}_{12}(\tau)=\frac{-1}{Z}\sum_{n,m}\frac{e^{-\beta(E_{m}-\mu N)}-e^{-\beta(E_{n}-E_{m})}}{E_{n}-E_{m}+i\Omega_{n}}\left\langle n \left| O_{2} \right| m \right\rangle \left\langle m \left| O_{1} \right| n \right\rangle }
So we conclude that two functions are the same if we only change Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\Omega_{n}\rightarrow\hbar(\Omega+i\eta)} in imaginary time function. In another words,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{D}_{12}(i\Omega_{n}\rightarrow\hbar(\Omega+i\eta))=D_{12}^{R}(\Omega)}
It is more convenient to work with Fourier transform of this operator, so define
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\varepsilon) = \frac{1}{i\hbar}\int_{0}^{\infty}dte^{\frac{i(\varepsilon+i\delta)t}{\hbar}}G(t)\Rightarrow G(\varepsilon) = (\varepsilon-\hat{H}+i\delta)^{-1} }
where to make the integrals converge, we need to add the infinitesimal quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\delta} to the exponents. sometimes, we consider energy in the complex plane and so we do not need to consider Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\delta} in that case. this fact warns that the physical significance of Green's functions may depend in an important way on the complex part of the energy, even when it is very small.
So Green's function contains full information about the time evolution of a particle: When Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} and energy has a positive imaginary part, the information is about the future, and when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} has a negative imaginary part, the information is about the past. As you can see the above formula shows that Green's function has a pole whenever Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}} has an eigenvalue, because if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mid\varepsilon_{n}>} are the eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}} with energies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon_{n}} , then
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G(\varepsilon)=\frac{1}{\varepsilon-\hat{H}} = \sum_{n}\frac{1}{\varepsilon-\hat{H}}\mid\varepsilon_{n}\rangle\langle\varepsilon_{n}\mid = \sum_{n}\frac{\mid\varepsilon_{n}\rangle\langle\varepsilon_{n}\mid}{\varepsilon-\varepsilon_{n}}} .
Let assume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon=\epsilon \pm i\eta}
, with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{r}}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta}
real. We will use
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{x+i\eta} = \frac{x-i\eta}{(x+i\eta)(x-i\eta)} = \frac{x-i\eta}{x^{2}+\eta^{2}}} .
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} is small and positive, we can split this into real and imaginary parts:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x}{x^{2}+\eta^{2}}-i\frac{\eta}{x^{2}+\eta^{2}} }
Now lets rewrite our Green's function in the same way:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G^{\pm}(\epsilon) = \sum_{n}\left(\frac{(\epsilon-\epsilon_{n})}{(\epsilon-\epsilon_{n})^{2}+\eta^{2}} \mp \frac{i\eta}{(\epsilon-\epsilon_{n})^{2}+\eta^{2}}\right)|\epsilon_{n}\rangle\langle\epsilon_{n}| = P\sum_{n}\frac{|\epsilon_{n}\rangle\langle\epsilon_{n}|}{\epsilon-\epsilon_{n}}\mp i\pi\sum_{n}\delta(\epsilon-\epsilon_{n})|\epsilon_{n}\rangle\langle\epsilon_{n}| }
Where we used Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\eta\rightarrow0}\frac{1}{x+i\eta} = P\frac{1}{x}-i\pi\delta(x)} .
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textrm{Tr}\left[G^{\pm}(\epsilon)\right] = P\sum_{n}\frac{1}{\epsilon-\epsilon_{n}} \mp i\pi\sum_{n}\delta(\epsilon-\epsilon_{n})}
The quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n}\delta\left(\epsilon-\epsilon_{n}\right)} is the density of states, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\epsilon)\!} . So, the imaginary part of Green's function keeps track of the density of states. Specificly:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\epsilon) = \mp\frac{1}{\pi}\Im \left( \textrm{Tr}\left[G^{\pm}(\epsilon)\right]\right)}
Collective Modes
Collective modes and Broken Symmetry
What is symmetry in physics?
A symmetry transformation is a change in our point of view that does not change the result of possible experiments. In particular, a symmetry transformation that is infinitesimally close to being trivial can be represented by a linear unitary operator that is infinitesimally close to the identity: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=1+i\epsilon t}
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} a real infintesimal. For this to be unitary and linear, t must be Hermitian and linear, so it is a candidate for an observable. Indeed, most(and perhaps all) of the observables of physics, such as angular momentum or momentum, arise in this way from symmetry transformations.
The set of symmetry transformations has certain properties that define it as a group. (From The Quantum Theory Of Fields Volume I,Steven Weinberg)
For a continuous symmetry,Neother's theorem states that there exists a corresponding conservation law. This came apparent to the physics community very early, in the times of Classical Mechanics domination, where cyclic variables (variables which do not appear in the physical system's Hamiltonian) were leading to the conservation of the correspondent momentum, i.e. if our Hamiltonian didn't contain Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} variable, then the conjugate momentum i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\phi}} was conserved.
In Quantum Field Theory, and in general in particle physics, symmetries play an essential role in our understanding of the fundamental forces and their properties. Someone can even exclude from the all possible Lagrangians and Hamiltonians terms that do not obey to the symmetries observed, although these terms appear to be completely legal from a physical standpoint.
There're several typical intrinsic symmetries in condensed matter systems. Examples:
Translation and Rotation symmetry(continuous), Parity symmetry(discrete)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{i}\frac{\textbf{p}_{i}^{2}}{2m}+\sum_{i<j}V(\mid\overrightarrow{\textbf{r}_{i}}-\overrightarrow{\textbf{r}_{j}}\mid)}
This is a many particle hamiltonian which includes the information of their kinetic energy and pairwise interactions.Hamiltonian invariant under translation or rotation of all coordinates indicates the global Galilean invariance of the system (continuous). Addtionally, this hamiltonian also invariant under space inversion about any point which indicates the parity invariant.
Translation and Rotation symmetry(discrete)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\frac{\textbf{p}^{2}}{2m}+\sum_{\overrightarrow{\textbf{R}}}V(\overrightarrow{\textbf{r}}-\overrightarrow{\textbf{R}})}
It can be used to describe the motion of electrons in a bravias lattace.The hamiltonian would present the point symmetry gained by the lattice.
Spin rotation symmetry(continuous)
Time reversal symmetry(discrete)
With the symmetry properties, we can obtain the conservation laws which would help us simplify the problems. What's more important, a conserved observable is related to some excitation.In the low temperature regimes, we would get some low energy excitations which dominates the gross properties of the system.Thus,when analyzing a certain condensed matter systems, we would first try to figure out its symmetry properties.
Symmetry breaking
Explicit symmetry breaking
Explicit symmetry breaking indicates a situation where the dynamical equations are not manifestly invariant under the symmetry group considered.
Spontaneous symmetry breaking
Spontaneous symmetry breaking where the laws are invariant but the system isn't because the background of the system, its vacuum, is non-invariant. Such a symmetry breaking is parameterized by an order parameter.(From wikipedia)
Mathematically, for a system which has a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_2 } symmetry, the pitchfork bifurcation might involved.
Why broken symmetry in low temperature?
We can build up the Free energy F, and then minimize it with respect to some field variable Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} . And then we can obtain several minimums, corresponds to several possible ground states. Basically, a system is dominated by its kinetic energy part while in high temperature and the potential part at low temperature . Thus, in order to minimize the potential energy, the system might go through a phase transition and break the original symmetry, there would come out some nonzero expectation value of operators which are the order parameters of the system. The quantity which would indicates that a phase transition has happened is the order parameters.
For example,the density wave of crystal, the magnetization of ferromagnet, the pair condensate of superconductor. The expressions are correspondingly Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_\textbf{k}\langle C^\dagger_\textbf{k}C_\textbf{k+q}\rangle} ,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_\textbf{k}\langle C^\dagger_{\textbf{k}\uparrow} C_{\textbf{k}\uparrow}-C^\dagger_{\textbf{k}\downarrow} C_{\textbf{k}\downarrow}\rangle} ,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle C_{\textbf{k}\uparrow}C_{\textbf{-k}\downarrow}\rangle} .
We should be careful when we apply the fundamental ergodicity postulate of statistical mechanics, that phase space of the system under this situation, actually sperates to different parts which have large potential barriers between them. Thus we cannot simply take the average over all configurations. If there're two minimums for example, they are totally different macroscopical configurations, not merely microscopical ones. Thus, in this situation, if we take average including this two, basically we would get zero of our order parameters and nothing exists. Thus, we need to refrain our calculations when system goes across the "barrier" into another different state.
Here, we could introduce the powerful Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi^4} theory to study some interacting field theory. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\int D\phi e^{-S[\phi]}, S[\phi]=\int d^dx(k(\partial\phi)^2+r\phi^2+g\phi^4) } The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi^4} model is extremely useful. For example, close to the critical point, the Ising model can be described by the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi^4} action. More generally, the long-range behavior of classical statical systems with a single order parameter is described by the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi^4} action. Within the context of statistical mechanics. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[\phi]} is known as the Ginzburg-Landau free energy functional. And notice that this functional has Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_2} symmetry reagrding Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} .
Then we need to minimize our functional S which directly related to F. We obtain the following equation: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2k\partial^2_x\phi=2r\phi+4g\phi^3} For a uniform solution( it happens when there's no external field), we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\phi+2g\phi^3=0} . Then wether we would get a real solution is based on the sign of r and g. Obviously, we can get a trivial solution that is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi=0} , another two is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi=\pm\sqrt{\frac{-r}{2g}}}
In the latter cases, our symmetry has already broken, and it happens when r and g has a different sign. This indicates that original solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi=0} may not be the stable one under some condition, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T<T_c} ,etc.
Collective phenomena
Minimum steps(for non-symmetry broken induced collective modes)
Write down the partition function as a path integral.
Introduce the auxiliary bosonic field.
Utilize the Hubbard–Stratonovich transformation, decouple the fields, evaluate the Matsubara frequency sum.
Take the factors of quadratic terms of fields, analytically continue it from imaginary time to real time retard Green's function, find out all the poles, We get the collective modes!!!
Symmetry broken case
(From Consented Matter Field Theory, Altland, Simons) The appearance of non-trivial ground states is just one manifestation of spontaneous symmetry breaking. Equally important, residual fluctuations around the ground state lead to the formation of soft modes (massless modes), i.e. field configurations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_\textbf{q}} whose action Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[\phi]} vanishes in the limit of long wavelength, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textbf{q}\rightarrow0} . Specifically, the soft modes formed on the top of a symmetry broken ground state are called Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textbf{Goldstone modes}} .
It's a special case of the so-called Goldstone bosons discovered by Yoichiro Nambu in the context of the BCS superconductivity mechanism, and subsequently elucidated by Jeffrey Goldstone. The -still eluding- Higgs boson is a manifestation of this mechanism. In particle physics the mechanism that creates those bosons exists almost in every corner. Different theories use this mechanism to prevent their particles from non having mass and to unify forces by incorporating this symmetry breaking mechanism to create the indermediate bosons, the carriers of each fundamental force. In each case we need different generators for every force. The bosons that are created through this process transform nonlinearly under the action of these generators, and can thus be excited out of the asymmetric vacuum by these generators.
As a rule, the presence of soft modes in a continuum theory has important phenomenological consequences. To understand this point, notice that the general structure of a soft mode action is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[\phi]=\sum_{\textbf{q},i}\phi_\textbf{q}(c^i_1|q_i|+c^i_2q^2_i)\phi_-\textbf{q}+ O(\phi^4,q^3)} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^i_{1,2}} are coefficients. The absence of a constant contribution to the action(i.e a contribution that does not vanish in the limit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textbf{q}\rightarrow0} ) signals the existence of long-range power-law correlations in the system. As we will see shortly, the vanishing of the action in the long-wavelength limit Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textbf{q}\rightarrow0} further implies that the contribution of the soft modes dominates practically all observable properties of the system.
What are the origin and nature of the soft Goldstone modes caused by the spontaneous breakdown of a symmetry? To address this point let us consider the action of a symmetry group element g on a symmetry broken ground state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_0} . By definition, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[g\psi_0]=S[\psi_0]} still assumes its extremal value. Assuming that g is close to the group identity, we may express Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g=\exp(\sum_a\phi_a T_a)} , where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {T_a}} are generators living in the Lie algebra of the group(differentiable) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_a} are some expansion coefficients. Expressing fluctuations around Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_0} in terms of the "coordinates" Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_a} , we conclude that the action Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[\phi]=0} . However, if we promote the global transformation to one with a weakly fluctuating spatial profile, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g\rightarrow g(\textbf{r}), \psi_0\rightarrow g(\textbf{r})\psi_0} , some price must be paid. That is, for a spatially fluctuating coordinate profile Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\phi_a(\textbf{r})}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[\phi]\neq0} , where the energy cost depends inversely on the fluctuation rate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda } of the field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} . The expansion of S in terms of gradients of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi } is thus bound to lead to a soft mode action of the type as the previous equation.
In view of their physical significance, it is important to ask how many independent soft mode exist. The answer can be straightforwardly given on the basis of the geometric picture developed above. Suppose our symmetry group G has dimension r, i.e. its Lie algebra is spanned by r linearly independent generators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_a} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=1,\ldots,r} . If the subgroup Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\sub G } has dimension s<r, s of these generators can be chosen so as to leave the ground state invariant. On the other hand, the remaining p=r-s generators inevitably create Goldstone modes. In the language of group theory, these generators span the coset space G/H. For example, for the ferromagnet, H=O(2) is the one-dimensional subgroup of rotations around the quantization axis(the z-axis). Since the rotation group has dimension 3, there must be two independent Goldstone modes. These can be generated by the action of the rotation, or angular momentum generators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{x,y}} acting on the z-aligned ground state. The coset space O(3)/O(2) can be shown to be isomorphic to the 2-sphere, i.e. the sphere traced out by the spins as they fluctuate around the ground state.
Finally, the connection between the coordinates parameterizing the Goldstone modes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_i, i=1,\ldots,p} residual "massive modes" Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_j, j=1,\ldots,n-p} , and the original coordinates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_i, i=1,\ldots,n} , of the problem, respectively, is usually nonlinear and sometimes not even very transparent. With problems more complex than the three prototypical examples mentioned above, it is usually profitable to first develop a good understanding of the geometry of the problem before specific coordinate systems are introduced.
Goldstone's theorem examines a generic continuous symmetry which is spontaneously broken; i.e., its currents are conserved, but the ground state (vacuum) is not invariant under the action of the corresponding charges. Then, necessarily, new massless (or light, if the symmetry is not exact) scalar particles appear in the spectrum of possible excitations. There is one scalar particle—called a Nambu–Goldstone boson—for each generator of the symmetry that is broken, i.e., that does not preserve the ground state. The Nambu–Goldstone mode is a long-wavelength fluctuation of the corresponding order parameter.(From wikipedia)
Basic concepts of BCS theory
Superconductivity involves an ordered state of conduction electrons in a metal, caused by the presence of a residual \textbf{attractive} interaction at the Fermi surface. At low temperatures, an attractive pairwise interaction can induce an instability of the electron gas towards the formation of bound pairs of time-reversed states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textbf{k}_\uparrow} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\textbf{k}_\downarrow } in the vicinity of the Fermi surface.
From where does an attractive interaction between charged particles appear? In conventional (BCS) superconductors, attractive correlations between electrons are due to the exchange of lattice vibrations, or phonons: The motion of an electron through a metal causes a dynamic local distortion of the ionic crystal. Crucially, this process is governed by two totally different time scales. For an electron, it takes a time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sim E^{-1}_F} to traverse the immediate vicinity of a lattice ion and to trigger a distortion out of its equilibrium position into a configuration that both particles find energetically beneficial. There're some elementary excitations, the Bogoliubov quasiparticles which have a energy gap.
Collective Modes in non-Symmetry Breaking Systems
Sound waves propagating through air or water are examples for collective modes. Such modes arise in media that don't break symmetry, such as ordinary gases and fluids. Those waves typically have wavelengths that are very large compared to the distance between neighboring particles, which is the reason why we will look at very small wave vectors. An example for a collective mode due to broken symmetry is a shear mode in a solid.
Remember that the partition function can be written as the Feynman path integral
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z = \int D(c^{*}, c) e^{-S}, }
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_0 = \frac{1}{\beta} \sum_{\omega_n} \sum_{k}(-i\omega_n + \epsilon_n-\mu) c_{k,\sigma}^{*} c_{k,\sigma}(\omega_n) }
is the action of the non-interacting system; while the action of the interacting system is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{int} = \frac1{\beta} \sum_{\Omega_n} \frac1{L^3}\sum_{q} V_q n_{-q}(-i\Omega_n) n_q(i\Omega_n) }
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_q (i\Omega_n) = \frac1{\beta}\sum_{\omega_n}\sum_k c^*_{k+q, \sigma} (i\omega_n + i\Omega_n) c_{k,\sigma}(i \omega_n) }
The partition function can be calculated via the Hubbard-Stratonovich Transformation, which can be motivated by the one-dimensional integral
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 = \frac1{\sqrt{\pi a}}\int\limits_{-\infin}^{\infin}dx e^{-\frac1a x^2}. }
The pre-factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\pi a} }
is simply the constant number that equals to the value of the integral.
In the language of path integrals this implies
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 = \frac1N \int D(\phi(r,\tau)) e^{ -\int\limits_0^{\beta}d\tau \int d^3r \phi(r)V^{-1}(r-r')\phi(r') }. }
Here the number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} resembles the pre-factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\pi a} } in the previous example. Rewriting the potential in momentum space, this identity allows to convert the partition function. This is done by a shift of the field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_q(i\Omega_n)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(i\Omega_n) = \tilde{\phi}(i\Omega_n) + i V_q n_q(i\Omega_n).}
The partition function, as introduced at the beginning of this chapter, simplifies thereby to
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} Z &= 1 \cdot \int D(c^*,c) e^{-S} \\ &= \frac1{N} \int D\phi_q(i\Omega_n)e^{ -\frac1{\beta} \sum_{\Omega_n}\frac1{L^3}\sum_q \phi_{-q}(-i \Omega_n) \frac1{V_q} \Phi_q(i\Omega_n)} \cdot \int D(c^*,c) e^{-S} \\ &\simeq Z_0 \int D\tilde\phi_q(i\Omega_n) \left[ \int D(c^*,c) e^{-S_0} e^{-\frac1{\beta}\sum_{\Omega_n} \frac1{L^3}\sum_q 2i n_{-q}(-i\Omega_n) \tilde \phi_q(i\Omega_n)}\frac1{Z_0} \right] e^{-\frac1{\beta}\sum\frac1{L^3}\sum_q \frac{\tilde\phi_{-q}(-i\Omega_n)\tilde\phi_{q}(i\Omega_n)}{V_q}}\\ &= \left\langle e^{-\frac1{\beta}\sum_{\Omega_n} \frac1{L^3}\sum_q 2i n_{-q} \tilde\phi_q(i\Omega_n)}\right\rangle\\ &\equiv \left\langle e^A\right\rangle \end{align}}
This can be calculated by a cumulant expansion, such that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} Z &= \left\langle e^A \right \rangle_0 \\ &= e^{\langle A \rangle_0 + \frac12 \left( \langle A^2 \rangle_0 -0 \langle A \rangle^2 \right) + \ldots} \end{align} }
Now, since the the average of the density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_q(i\Omega_n)} is equal to zero, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle n_q(i\Omega_n)\right\rangle = 0, \quad \forall q\neq 0 \and \Omega_n\neq 0, }
we only have to calculate the term with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle A^2\rangle} in the exponent. This term contains the average of two density operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_q(i\Omega_n)} , which can be evaluated using the Wick's theorem.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n_{-q}(-i\Omega_n)n_{q'}(i\Omega_n')\rangle = \frac1{\beta^2} \sum_{\omega_n,\omega_n'} \sum_{k,k'} \langle c^*_{k-q,\sigma}(i\omega_n-i\Omega_n)c_{k,\sigma}(i\omega_n) c^*_{k'+q',\sigma'}(i\omega_n'+i\Omega_n')c_{k',\sigma'}(i\omega_n') \rangle_0 }
Since we have two creation operators and two annihilation operators, two possible contractions are possible. However, one of these contractions is a non-connected Feynman diagram and so, according to the linked cluster theorem, we only have to compute the connected one. Due to Kronecker-delta symbols (arising from the contractions) we will be left with only one sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} and one sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} . The resulting sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} can be written as an integral over a continuum (by taking the appropriate limit of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L\rightarrow\infin} ), while the sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} is written as a contour integral. The result of this exercise is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac Z{Z_0} \simeq \int D\phi e^{S_{eff}(\phi)}, }
where the effective action is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{eff}(\phi) = \frac1{\beta}\sum_{\Omega_n}\frac1{L^3} \sum_q\left(\frac1{V_q}-2 \mathcal N\Pi_q(i\Omega_n) \right) \phi_{-q}(i\Omega_n) \phi_q(i\Omega_n) + \mathcal O(\phi^4).}
Here we use the degeneracy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}} of each level. This action is expressed in terms of an integral that we are about to solve, namely
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_q(i\Omega_n) = \int \frac{d^3k}{(2\pi)^3} \frac{n_F(\epsilon_k)-n_F(\epsilon_{k-q})} {\epsilon_k - \epsilon_{k-q}-i\Omega_n}. }
In this expression Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_F(E)=\frac1{e^{\frac{E-\mu}{kT}+1}}} is the Fermi-Dirac distribution function, together with the chemical potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , the Boltzmann factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B} and the temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} .
As said before, our special interest is pointed towards density waves in an electron gas. So finally, the degeneracy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}}
will be set equal to 2. Notice that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_q(i\Omega_n)}
couples to density.
We also said in the beginning of the chapter that wavelengths of such excitations are typically very long compared to the distance between molecules; or, in case of a plasma, the distance between electrons. Therefore, when we calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_q(i\Omega_n)}
we look at the limit of very small wave vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q}
, and we will also consider small temperatures. For an electron gas the energy dispersion is, of course, quadratic in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k}
, being Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k=\frac{\hbar^2k^2}{2m}}
.
Therefore, let us assume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |q|\ll k_F}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\ll \mu}
.
In that case the difference
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} n_F(\epsilon_k)-n_F(\epsilon_{k-q}) \end{align}}
in the integrand of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_q(i\Omega_n)} has no contribution for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k} being far away from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_F} . Hence we can expand the numerator of the integrand by writing
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} n_F(\epsilon_{k-q}) &= n_F(\epsilon_{k}+\epsilon_{k-q}-\epsilon_{k})\\ &\simeq n_F(\epsilon_k) + n_F'(\epsilon_k) (\epsilon_{k-q} - \epsilon_k). \end{align} }
With this approximation the quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_q(i\Omega_n)} can be calculated via the Sommerfeld expansion, i.e. after integration over the angles we multiply the expression by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1=\int\limits_{-\infin}^{\infin}d\epsilon \delta(\epsilon-\epsilon_F)} and exchange the integrals over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} . Roughly speaking, the integral over k equals the density of states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\epsilon)} . Notice that we add Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0=-i\Omega_n+i\Omega_n} to the numerator of the integrand. The calculation is as follows.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \Pi_q(i\Omega_n) &= \Pi_q(i\Omega_n) = \int \frac{d^3k}{(2\pi)^3} \frac{(n_F(\epsilon_k)-n_F(\epsilon_{k-q})-i\Omega_n) + i\Omega_n} {\epsilon_k - \epsilon_{k-q}-i\Omega_n}.\\ &= \Pi_q(i\Omega_n) = \int \frac{d^3k}{(2\pi)^3} ( 1 + \frac{i\Omega_n}{\frac{\hbar^2 k^2}{2m}- \frac{\hbar^2}{2m} (k-q)^2 - i\Omega_n} )\\ &= \Pi_q(i\Omega_n) = \int \frac{d^3k}{(2\pi)^3} ( 1 + \frac{i\Omega_n}{\frac{\hbar^2}{2m} kq\cos(\theta) - \frac{\hbar^2q^2}{2m} - i\Omega_n})\\ &= \int\limits_{-\infin}^{\infin} d\epsilon N(\epsilon) n_F'(\epsilon) \left( 1+ \frac{i\Omega_n}{2 v_F\hbar q} \ln \frac{v_F\hbar q-i\Omega_n}{-v_F\hbar q-i\Omega_n} \right) \\ &= -N(\epsilon_F) \left(1 + \frac{i\Omega_n}{2v_F\hbar q} \ln\left( \frac{i\Omega_n - v_F\hbar q}{i\Omega_n + v_F \hbar q} \right)\right). \end{align} }
The last step uses that in the low-temperature limit the derivative of the Fermi distribution function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_F'(\epsilon)} only has a contribution at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon=\epsilon_F} , where it is sharply peaked. We introduced the Fermi velocity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_F=\hbar k_F/m} , which is the velocity of Fermions that are right on the Fermi surface.
Now, the expression
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{V_q} - 2\mathcal N\Pi_q(i\Omega_n)}
in the effective action Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{eff}} defined above is the inverse of a Green's function. So in order to get knowledge of the spectrum of the system, we seek the zeros of the named expression.
Zero Sound and Plasma Frequency
Now if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega < \upsilon_{F} \hbar q} i.e. numerator is -ve! then we pick up an imaginary term in this equation which doesnot vanish even when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta \to 0 } So the solution is above the window Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 < \Omega < \upsilon_{F} \hbar q}
For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega > \upsilon_{F} \hbar q} we get, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\epsilon_{F}) \left ( 1+ \frac{\Omega}{2\upsilon_{F} \hbar q} ln \left ( \frac{\Omega -\upsilon_{F} \hbar q}{\Omega +\upsilon_{F} \hbar q} \right ) \right ) \to finite }
Therefore we can find the solution from following equation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2N N(\epsilon_{F}) \left ( 1+ \frac{\Omega}{2\upsilon_{F} \hbar q} ln \left ( \frac{\Omega -\upsilon_{F} \hbar q}{\Omega +\upsilon_{F} \hbar q} \right ) \right ) + \frac{1}{V_{q}} = 0 }
Lets define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left ( 1+ \frac{\Omega}{2\upsilon_{F} \hbar q} ln \left ( \frac{\Omega -\upsilon_{F} \hbar q}{\Omega +\upsilon_{F} \hbar q} \right ) \right ) = \theta (\frac{\Omega}{\upsilon_{F} \hbar q}) }
So we can write,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta (\frac{\Omega}{2\upsilon_{F} \hbar q}) = \frac{-1}{2N N(\epsilon_{F})} \frac{1}{V_{q}}}
We can expand Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta (\frac{\Omega}{2\upsilon_{F} \hbar q}) = - \frac{1}{3}\frac{\hbar^2 q^2 \upsilon^2 _F }{\Omega^2}}
For Long range interaction: e.g Coulomb interaction: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{q} = \frac{2\pi e^2}{q^2}}
Therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-1}{2N N(\epsilon_{F})} \frac{2\pi e^2}{q^2} = \frac{-1}{3}\frac{\hbar^2 q^2 \upsilon^2 _F }{\Omega^2} }
We will get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega^2 = \frac {2N}{3}N(\epsilon_{F}) 2\pi e^2 \hbar^2 \upsilon^2 _F }
Now using density of states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\epsilon_{F})= \frac{m k_{F}}{2\pi^2 \hbar ^2 }} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 2} ,spin degeneracy to reach to the following equation of Plasma Frequency,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega^2_{pl} = \frac {4\pi e^2 \rho}{m}} , Where density of particle,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = \frac{k^3 _{F}}{3\pi^2}}
For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q \to 0 } we get a gapped collective mode whose frequecny starts from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-1}{2N N(\epsilon_{F})} \frac{2\pi e^2}{q^2} = \frac{-1}{3}\frac{\hbar^2 q^2 \upsilon^2 _F }{\Omega^2} }
For finite range interaction: Bold text: e.g. Yukawa potential: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{q} = \frac{V_o}{q^2 + \xi ^{-2}}}
where, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{q=0} = finite }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \theta (\frac{\Omega}{2\upsilon_{F} \hbar q}) = \frac{-1}{ N(\epsilon_{F})} \frac{1}{V_{q}}}
For large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{q=0}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-1}{4 N(\epsilon_{F})} \frac{1}{V_{q=0}} = \frac{-1}{3}\frac{\hbar^2 q^2 \upsilon^2 _F }{\Omega^2} } As q Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \to 0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega \sim q} , then we arrive the following equation for the frequency of Zero Sound, for which the low-q behavior of the collective mode is completely different than for the coulomb potential, Since finite range potentials are less singular than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {1}{q^2}} at low q.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_{zs} = \sqrt{\frac{4N(\epsilon_{F}) V_{q=0}}{3}} \upsilon_F \hbar q}
The zero sound is physically different than ordinary first sound despite the similar dispersion relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega = c q} Zero Sound is built out of quasiparticles, so at finite temperatures the frequency must be high enough that the quasiparticles do not decay,i.e. the collisions do not dominate. At zero temperature the lifetime becomes infinite as quasiparticles approach the fermi surface, so zero sound proopagates at all frequencies. Zero sound is a collective mode sustained by the cogerent self-consistent interaction arising from neighbouring particles. In contrast, thermodynamic sound can propagate only if the system is in local thermodynamic equilibrium, this condition requires that interparticle collision Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} is shorter compared to period of oscillation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2\pi}{\Omega}} .
Fluctuation-Dissipation Theorem
In statistical mechanics people are mostly concerned with the evaluation of statistical averages of the various physical quantities; these averages represent, with a high degree of accuracy, the results expected from relevant measurements on the given system in equilibrium. Nevertheless, there do occur deviations from, or fluctuations about, these mean values. Though they are generally small, their study is of great physical interest for several reasons.
Firstly, it enables us to develop a mathematical scheme with the help of which the magnitude of the relevant fluctuations, under a variety of physical situations, can be estimated. Not surprisingly, we find that while in a single-phase system the fluctuations are thermodynamically negligible they can assume considerable importance in multi-phase systems, especially in the neighborhood of a critical point. In the latter case, we obtain a rather high degree of spatial correlation among the molecules of the system which, in turn, gives rise to phenomena such as critical opalescence.
Secondly, it provides a natural framework for understanding a class of phenomena that come under the heading "Brownian motion"; these phenomena relate properties such as the mobility of a fluid system, its coefficient of diffusion, etc. with temperature through the so-called Einstein relations. The mechanism of Brownian motion is vital in formulating, and in a certain sense answering, questions as to how "a given physical system, which is not in a state of equilibrium, finally approaches such a state" while "a physical system, which is already in a state of equilibrium, persists to stay in that state".
Thirdly, the study of fluctuations, as a function of time, leads to the concept of certain "correlation functions" that play a vital role in relating the dissipative properites of a system, such as the viscous resistance of a fluid or the electrical resistance of a conductor, with the microscopic properties of the system in a state of equilibrium; this relationship (between irreversible processes on one hand and equilibrium properties on the other) manifests itself in the so-called fluctuation-dissipation theorem. At the same time, a study of the "frequency spectrum" of fluctuations, which is related to the time-dependent correlation function through the fundamental theorem of Wiener and Khinchine, is of considerable value in assessing the "noise" met with in electrical circuits as well as in the transmission of electromagnetic signals.
Examples of fluctuation-dissipation theorem are
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle E^2 \rangle - \langle E \rangle^2 = k_B T^2 C_V }
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle N^2 \rangle - \langle N \rangle^2 = \frac{\bar{N} k_B T \kappa_T}{v} }
whereby a fluctuation is related to an appropriate "susceptibility". In the case of energy fluctuations the relevant susceptibility is the specific heat at constant volume, and in the case of density fluctuations it is the thermal compressibility.
In general, the fluctuation-dissipation theorem relates a correlation function, or "fluctuation", to the imaginary part of a susceptibility, or "dissipation". We will now derive this relation. Let us begin with a real-time correlation function,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(t-t')=\langle \hat{O}(t)\hat{O}(t')\rangle=\frac{1}{Z}\sum_{mn}e^{-\beta(E_n-\mu N)}\langle n|\hat{O}(t)|m\rangle\langle m|\hat{O}(t')|n\rangle=\frac{1}{Z}\sum_{mn}e^{-\beta(E_n-\mu N)}e^{i(E_n-E_m)(t-t')/\hbar}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle.}
The Fourier transform of this function is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\omega)=\int_{-\infty}^{\infty}dt\,S(t)e^{i\omega t}=\frac{1}{Z}\int_{-\infty}^{\infty}dt\,\sum_{mn}e^{-\beta(E_n-\mu N)}e^{i(E_n-E_m+\hbar\omega)t/\hbar}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{2\pi\hbar}{Z}\int_{-\infty}^{\infty}dt\,\sum_{mn}e^{-\beta(E_n-\mu N)}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle\delta(E_n-E_m+\hbar\omega).}
Now we consider the response function,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^R(t-t')=-\frac{i}{\hbar}\theta(t-t')\langle [\hat{O}(t),\hat{O}(t')]\rangle=-\frac{i}{\hbar}\frac{1}{Z}\theta(t-t')\sum_{mn}e^{-\beta(E_n-\mu N)}[\langle n|\hat{O}(t)|m\rangle\langle m|\hat{O}(t')|n\rangle-\langle n|\hat{O}(t')|m\rangle\langle m|\hat{O}(t)|n\rangle]} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{i}{\hbar}\frac{1}{Z}\theta(t-t')\sum_{mn}e^{-\beta(E_n-\mu N)}[e^{i(E_n-E_m)(t-t')/\hbar}-e^{-i(E_n-E_m)(t-t')/\hbar}]\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle,}
or, exchanging Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} in the second term,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^R(t-t')=-\frac{i}{\hbar}\frac{1}{Z}\theta(t-t')\sum_{mn}[e^{-\beta(E_n-\mu N)}-e^{-\beta(E_m-\mu N)}]e^{i(E_n-E_m)(t-t')/\hbar}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle.}
We will now take the Fourier transform of this expression. Introducing a convergence factor, we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D^R(\omega)=\int_{-\infty}^{\infty}dt\,D^R(t)e^{i\omega t}=-\frac{i}{\hbar}\frac{1}{Z}\int_{0}^{\infty}dt\,\sum_{mn}[e^{-\beta(E_n-\mu N)}-e^{-\beta(E_m-\mu N)}]e^{i(E_n-E_m+\hbar\omega)t/\hbar}e^{-\hbar\eta t}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{1}{\hbar}\frac{1}{Z}\sum_{mn}\frac{e^{-\beta(E_n-\mu N)}-e^{-\beta(E_m-\mu N)}}{E_m-E_n-\hbar(\omega+i\eta)}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle.}
If we take the imaginary part of this expression, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Im}\,D^R(\omega)=-\frac{1}{\hbar}\frac{1}{Z}\sum_{mn}\frac{\hbar\eta[e^{-\beta(E_n-\mu N)}-e^{-\beta(E_m-\mu N)}]}{(E_m-E_n-\hbar\omega)^2+\hbar^2\eta^2}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle,}
or, taking the limit, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta\rightarrow 0} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Im}\,D^R(\omega)=-\frac{\pi}{Z}\sum_{mn}[e^{-\beta(E_n-\mu N)}-e^{-\beta(E_m-\mu N)}]\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle\delta(E_n-E_m+\hbar\omega).}
We may replace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_m} with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n+\hbar\omega} because of the delta function. If we do so, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Im}\,D^R(\omega)=-\frac{\pi}{Z}(1-e^{-\beta\hbar\omega})\sum_{mn}e^{-\beta(E_n-\mu N)}\langle n|\hat{O}|m\rangle\langle m|\hat{O}|n\rangle\delta(E_n-E_m+\hbar\omega).}
If we compare this expression to the one we obtained for the correlation function, we find that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\omega)=-\frac{2\hbar}{1-e^{-\beta\hbar\omega}}\text{Im}\,D^R(\omega),}
which is the relation we sought.
The most striking feature of this theorem is that it relates, in a fundamental manner, the fluctuations of a physical quantity pertaining to the equilibrium state of the given system to a dissipative process which, in practice, is realized only when the system is subject to an external force that drives it away from equilibrium. Consequently, it enables us to determine the non-equilibrium properties of a given system on the basis of a knowledge of the thermal fluctuations occuring in the system when the system is in one of its equilibrium states!
Saddle point approximation and broken symmetry
Analytic Landscape
In analyzing problems in mathematical physics, one often finds it desirable to know the behavior of a function for large values of the variable or some parameter s, that is, the asymptotic behavior of the function. Specific examples are furnished by the gamma function and various Bessel functions. All these analytic functions are defined by integrals
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s) = \int_{C}^{} F(z,s) dz } ......... (2.5.1)
where F is analytic in z and depends on a real parameter s. We write F(z) simply whenever possible.
Normally we evaluate such definite integrals of analytic functions along the real axis by deforming the path C to C' in the complex plane, so that |F| becomes small for all z on C'. This method succeeds as long as only isolated poles occur in the area between C and C'. The poles are taken into account by applying the residue theorem. The residues give a measure of the simple poles where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F| \rightarrow \infty } , which usually dominate and determine the value of the integral.
The behavior of such an integral in Eq. (2.5.1) clearly depends on the absolute value |F| of the integrand. Moreover, the contours of |F| often become more pronounced as s becomes large. Let us focus on a plot of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(x+iy)|^2 = U^2(x,y) + V^2(x,y) } , rather than the real part ReF = U and the imaginary part ImF = V separately. Such a plot of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F|^2 } over the complex plane is called the analytic landscape after Jensen who, in 1912, proved that it has only saddle points and troughs, but no peaks. Moreover, the troughs reach down all the way to the complex plane. In the absence of (simple) poles, saddle points are next in line to dominate the integral in Eq. (2.5.1). Hence the name saddle point method. At a saddle point the real part U of F has a local maximum, say, which implies that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial U}{\partial x} + \frac{\partial U}{\partial y} = 0 }
and therefore by the use of the Cauchy-Riemann conditions
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial V}{\partial x} + \frac{\partial V}{\partial y} = 0 }
so that V has a minimum, or vice versa, and F'(z)=0. Jensen's theorem prevents U and V from having both a maximum or minimum. See the Figure below for a typical shape. We will choose the path C so that it runs over the saddle point and in the valleys elsewhere. If there are several saddle points, we treat each alike, and their contributions will add to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s \rightarrow \infty) } .
To prove that there are no peaks, assume there is one at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{0}} . That is, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z_{0})|^2 > |F(z)|^2 } for all z in the neighborhood Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z-z_{0}| \le r } . If
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(z) = \sum_{n=0}^{\infty} a_n (z-z_{0})^n }
is the Taylor expansion at zo, the mean value m(F) on the circle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = z_{0}+ r e^{i \phi} } becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m(F) = \frac{1}{2 \pi} \int_{0}^{2 \pi} |F(z_{0}+r e^{i \phi})|^2 d \phi } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2 \pi} \int_{0}^{2 \pi} \sum_{m,n=0}^{\infty} a_{m}^{*} a_{n} r^{m+n} e^{i(n-m) \phi} d \phi } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \sum_{n=0}^{\infty} |a_n|^2 r^{2n} > |a_o|^2 = |F(z_{0})|^2} (2.5.2)
using orthogonality, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2 \pi} \int_{0}^{2 \pi} e^{i(n-m) \phi} d \phi = \delta_{n,m} } . Since m(F) is the mean value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F|^2 } on the circle of radius r, there must be a point z1 on it so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z_{1})|^2 > m(F) > |F(z_{0})|^2 } , which contradicts our assumption. Hence there can be no such peak.
Next, let us assume there is a minimum at zo so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 < |F(z_0)|^2 < |F(z)|^2 } for all z in the neighborhood of zo. In other words, the dip in the valley does not go down to the complex plane. Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z)|^2 > 0 } and, since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/F(z) } is analytic there, it has a Taylor expansion and zo would be a peak of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/|F(z)|^2 } , which is impossible. This proves Jensen's theorem. We now return to the integral in Eq. (2.5.1).
Saddle Point Method
Since each saddle point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{0}} necessarily lies above the complex plane, that is, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z_{0})|^2 > 0 } , we write F in exponential form, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{f(z,s)} } in its vicinity without loss of generality. At zo the tangential plane is horizontal, i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\partial F / \partial z)|_{z=z_{0}} = 0 } , or equivalently Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\partial f / \partial z)|_{z=z_{0}} = 0 } . At zo, f has a power series
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(z) = f(z_{0}) + \frac{1}{2} f''(z_{0})(z-z_{0})^2 + ..... } ..... (2.5.3)
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(z) = f(z_{0}) + \frac{1}{2} (f''(z_{0}) + \epsilon)(z-z_{0})^2 } .....(2.5.4)
upon collecting all higher powers in the (small) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } . Let us take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f''(z_{0}) \neq 0 } for simplicity. Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f''(z_{0})(z-z_{0})^2 = - t^2 } .....(2.5.5)
for real t defines a line through zo (saddle point axis in the Figure). At Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{0}} , t=0. Along the axis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Im[f''(z_{0})(z-z_{0})^2] } is zero and v = Imf(z) ~ Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Im\; f(z_{0})} is constant if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } in Eq. (2.5.4) is neglected. Equation (2.5.5) can also be expressed in terms of angles,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle arg(z-z_{0}) = \frac{\pi}{2} - \frac{1}{2} arg f''(z_{0}) = constant } ....(2.5.6)
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z)|^2 = e^{2 Ref} } varies monotonically with Ref, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z)|^2 \rightarrow e^{-t^2} } falls off exponentially from its maximum at t = 0 along this axis. Hence the name steepest decent. The line through Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{0}} defined by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f''(z_{0})(z-z_{0})^2 = + t^2 } ....(2.5.7)
is orthogonal to this axis (dot-dashed in the Figure), which is evident from its angle
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle arg(z-z_{o}) = - \frac{1}{2} arg f''(z_{o}) = constant } ....(2.5.8)
when compared with Eq. (2.5.6). Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z)|^2 } grows exponentially.
The curves Ref(z) = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ref(z_{o})} go through zo so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Re[(f''(z_o)+ \epsilon)(z-z_o)^2] = 0 } , or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (f''(z_o)+ \epsilon)(z-z_o)^2 = it } for real t. Expressing this in angles as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle arg(z-z_o) = \frac{\pi}{4} - \frac{1}{2} arg(f''(z_o)+ \epsilon), t > 0 } ....(2.5.9a)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle arg(z-z_o) = - \frac{\pi}{4} - \frac{1}{2} arg(f''(z_o)+ \epsilon), t < 0 } ....(2.5.9b)
and comparing with Eqs. (2.5.6) and (2.5.8) we note that these curves (dot-dashed in the Figure) divide the saddle point region into four sectors, two with Ref(z) > Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ref(z_o)} (hence |F(z)| > Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z_o)|} ) shown shaded in the Figure, and two with Ref(z) < Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ref(z_o)} (hence |F(z)| < Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |F(z_o)|} ) . They are at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm (\pi / 4) } angles from the axis. Thus, the integration path has to avoid the shaded areas where |F| rises. Now we are ready to specialize the integrand F further in order to tie up the path selection with the asymptotic behavior as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s \rightarrow \infty } .
We assume that s appears linearly in the exponent, that is, we replace Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{f(z,s)} \rightarrow e^{s f(z)} } . This dependence on s ensures that the saddle point at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_0 } grows with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s \rightarrow \infty } , as is the case in most applications in physics. In order to account for the region far away from the saddle point that is not influenced by s, we include another analytic function g(z) that varies slowly near the saddle point and is independent of s. Altogether then our integral has the more appropriate and specific from
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s) = \int_{C}^{} g(z) e^{s f(z)} dz } (2.5.10)
The path of the steepest decent is the saddle point axis when we neflect the higher order terms, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} , in Eq. (2.5.4). With Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } , the path of the steepest decent is the curve close to the axis within the unshaded sectors, where v = Imf(z) is strictly constant, while Imf(z) is only approximately constant on the axis. We approximate I(s) by the integral along the piece of the axis inside the patch in the Figure, where (compare with Eq. (2.5.5)),
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = z_o + x e^{i \alpha}, \alpha = \frac{\pi}{2} - \frac{1}{2} argf''(z_o), a \le x \le b } (2.5.11)
We find
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s) \rightarrow e^{i \alpha} \int_{a}^{b} g(z_o + x e^{i \alpha}) e^{s f(z_o + x e^{i \alpha})} dx } (2.5.12a)
and the omitted part is small and can be estimated because Re[f(z)-Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(z_o)} ] has an upper negative bound, -R say, that depends on the size of the saddle point patch in the Figure (i.e., the values of a, b in Eq. (2.5.11)) that we choose. In Eq. (2.5.12) we use the power expansions
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(z_o + x e^{i \alpha}) = f(z_o) + \frac{1}{2} f''(z_o) e^{2i \alpha} x^2 + ... }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(z_o + x e^{i \alpha}) = g(z_o) + g'(z_o) e^{i \alpha} x + ... } (2.5.12b)
and recall from Eq. (2.5.11) that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} f''(z_o) e^{2i \alpha} = -\frac{1}{2} |f''(z_o)| < 0 }
We find for the leading term
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s) = e^{i \alpha} g(z_o) e^{s f(z_o)} \int_{a}^{b} e^{-\frac{1}{2} s |f''(z_o)| x^2} dx } (2.5.13)
As the integrand in Eq. (2.5.13) is essentially zero when x departs appreciably from the origin, we let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b \rightarrow \infty } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a \rightarrow -\infty } . The small error involved is straightforward to estimate. Noting that the remaining integral is just a Gauss error integral,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty} e^{-\frac{1}{2} a^2 x^2} dx = \frac{\sqrt{2 \pi}}{a}}
we finally obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(s) = \frac{\sqrt{2 \pi} g(z_o) e^{s f(z_o)} e^{i \alpha}}{|s f''(z_o)|^{1/2}} } (2.5.14)
where the phase Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha } was introduced in Eq. (2.5.11).
Final Remark. We assumed that the only significant contribution to the integral came from the immediate vicinity of the saddle point(s) z = zo. This condition must be checked for each new problem.
Example. Asymptotic Form of the Factorial Function s!
In many physical problems, particularly in the field of statistical mechanics, it is desirable to have an accurate approximation of the gamma or factorial function of very large numbers. The factorial function may be defined by the Euler integral
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s! = \int_{0}^{\infty} \rho^s e^{-\rho} d \rho = s^{s+1} \int_{0 C}^{\infty} e^{s(lnz - z)} dz } (2.5.15)
Here we have made the substitution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = zs } in order to throw the integral into the form required by Eq. (2.5.10). As before, we assume that s is real and positive, from which it follows that the integrand vanishes at the limits 0 and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \infty } . By differentiating the z-dependence appearing in the exponent, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{df(z)}{dz} = \frac{d}{dz} (lnz - z) = \frac{1}{z} - 1 } (2.5.16)
which shows that the point z = 1 is a saddle point. We let
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z - 1 = x e^{i \alpha}, \alpha = \frac{\pi}{2} - \frac{1}{2} arg f''(1) } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{\pi}{2} - \frac{1}{2} arg(-1) = 0 } (2.5.17)
with small x to describe the contour in the vicinity of the saddle point. Substituting into Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(z) = lnz - z } , we develop a series expansion
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(z) = ln(1 + x e^{i \alpha}) - (1 + x e^{i \alpha}) } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = x e^{i \alpha} - \frac{1}{2} x^2 e^{2i \alpha} + ... - 1 - x e^{i \alpha} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = - 1 - \frac{1}{2} x^2 e^{2i \alpha} } (2.5.18)
From this we see that the integrand takes on a maximum value (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-s} } ) at the saddle point if we choose our contour C to follow the real axis, a conclusion that we could have reached more or less intuitively.
Direct substitution into Eq. (2.5.14) with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = 0 } now gives
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s! = \frac{\sqrt{2 \pi} s^{s+1} e^{-s}}{|s (-1^{-2})|^{1/2}} } (2.5.19)
Thus the first term in the asymptotic expansion of the factorial function is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s! = \sqrt{2 \pi s} s^s e^{-s} } (2.5.20)
This result is the first term in Stirling's expansion of the factorial function. The method of steepest decent is probably the easiest way of obtaining this first term.
In the foregoing example the calculation was carried out by assuming s to be real. This assumption is not necessary. We may show that Eq. (2.5.19) also holds when s is replaced by the complex variable w, provided only that the real part of w is required to be large and positive.
Hubbard Model
The Hubbard model describes one simple way to understand the interactions between electrons in a lattice structure and how this gives rise to different properties such as the insulating, magnetic, and superconducting behaviors observed in solids. Developed in 1963, the Hubbard Model manifests physical properties relevant to many of the most subtle and beautiful properties of solid state systems. The Hubbard Model has been solved completely in one-dimension using both analytical and numerical methods. Despite the fact the Hubbard Model has not been solved for higher dimensions, numerical methods for solving interesting applications of the Hubbard Model is well researched today.
The Hamiltonian of the system consists of two terms, a kinetic term and a potential interaction term. Both terms are written as a combination of creation and annihilation operators (see examples below). The kinetic term describes the tunneling (hopping) of electrons and the potential term describes 'on-site' interactions. Important to note is that there is a regular array of nuclear positions in a solid, which for simplicity we consider to be fixed, therefore we will not worry about lattice vibrations. In a solid where electrons can move around, the electrons interact via a screened Coulomb interaction. The biggest interaction will be for two electrons on the same atom. Simple Hubbard models stop at these considerations, so that interactions are modeled by a term which is zero if the atom is void of electrons or has only a single electron, but has the value U if the atom has two electrons.
Below are two examples of the Hubbard model. The first is a general explanation of the Hamiltonian of Hubbard models while the second is an expansion of these models.
Example 1:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -t \sum_{<j,l>\sigma}^{} c_{j\sigma}^{\dagger} c_{l\sigma} + U \sum_{j}^{} n_{j\uparrow} n_{j\downarrow} - \mu \sum_{j}^{} (n_{j\uparrow}+ n_{j\downarrow}) }
The first term is the kinetic energy and describes site hopping. The fermions are only allowed to hop between two adjacent sites, j and l. The second term represents the interaction energy between the two populations, spin up and spin down. It searches all the sites (sum over j) and when it finds a site which is doubly occupied with two fermions (having spin up and down) adds an interaction energy because of the spin interaction. The last term allows us to control the number of fermions using the chemical potential.
By controlling the number of fermions, we can define the sites to be half-filled. In the Hubbard model, a completely filled site contains two fermions, so half-filled is defined as one fermion per site. By utilizing half-filled sites, we can further explore the different phenomena that may arise, like anti-ferromagnetic order, Mott transition (insulators) etc.
Example 2:
The Hamiltonian of the Hubbard model can also be written as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -t \sum_{<rr'>}^{} \sum_{\sigma = \uparrow \downarrow} [C_{\sigma}^{+}(r) C_{\sigma}(r') + C_{\sigma}^{+}(r') C_{\sigma}(r)] + u \sum_{r}^{} C_{\uparrow}^{+}(r) C_{\uparrow}(r) C_{\downarrow}^{+}(r) C_{\downarrow}(r) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -t \sum_{r, \sigma}^{} \sum_{\vec{\delta} = \hat{x}, \hat{y}}^{} [C_{\sigma}^{+}(r) C_{\sigma}(r+ \delta) + C_{\sigma}^{+}(r+ \delta) C_{\sigma}(r)] + u \sum_{r}^{} C_{\uparrow}^{+}(r) C_{\uparrow}(r) C_{\downarrow}^{+}(r) C_{\downarrow}(r)}
assuming that on average, there is only one particle per site.
Note that this Hamiltonian has global U(1) symmetry (charge conservation) :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\sigma}(r) \rightarrow e^{i \theta} C_{\sigma} (r) } ,
as well as global SU(2) symmetry (spin conservation):
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\sigma} \rightarrow u_{\alpha \beta} C_{\beta}(r) = (e^{i \vec{\theta} \cdot \vec{\sigma}})_{\alpha \beta} C_{\beta}(r) }
which is not obvious at this moment. To see this, let us re-express the second term in terms of spin operators: (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar = 1 } )
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(r) = \frac{1}{2} C_{\alpha}^{+}(r) \vec{\tau}_{\alpha \beta} C_{\beta}(r) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}^2(r) = \frac{1}{4} C_{\alpha}^{+}(r) \tau_{\alpha \beta}^{a} C_{\beta}(r) C_{\gamma}^{+}(r) \tau_{\gamma \delta}^{a} C_{\delta}(r) }
Notice that any 2x2 matrix can be expressed in terms of Pauli matriies and unit matrix, that is,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M = \frac{1}{2} 1_{2x2} Tr[M] + \frac{1}{2} \sum_{a=1}^{3} \tau^a Tr[M \tau^a] }
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{ij} = \frac{1}{2} \delta_{ij} \delta_{kl} M_{lk} + \frac{1}{2} \sum_{a=1}^{3} \tau_{ij}^a M_{kl} \tau_{lk}^a }
Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial M_{ij}}{\partial M_{\alpha \beta}} = \frac{1}{2} \delta_{ij} \delta_{kl} \frac{\partial M_{lk}}{\partial M_{\alpha \beta}} + \frac{1}{2} \sum_{a=1}^{3} \tau_{ij}^a \tau_{lk}^a \frac{\partial M_{kl}}{\partial M_{\alpha \beta}} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{i \alpha} \delta_{j \beta} = \delta_{ij} \delta_{kl} \delta_{l \alpha} \delta_{k \beta} + \frac{1}{2} \sum_{a=1}^{3} \tau_{ij}^a \tau_{lk}^a \delta_{k \alpha} \delta_{l \beta} }
Therefore
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{a=1}^{3} \tau_{ij}^a \tau_{\beta \alpha}^a = 2 \delta_{i \alpha} \delta_{j \beta} - \delta_{ij} \delta_{\alpha \beta} }
or, relabeling the indicies
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{a=1}^{3} \tau_{\alpha \beta}^a \tau_{\gamma \delta}^a = 2 \delta_{\alpha \delta} \delta_{\beta \gamma} - \delta_{\alpha \beta} \delta_{\delta \gamma} }
Now we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S^2 = \frac{1}{4} \sum_{a=1}^3 \tau_{\alpha \beta}^{a} \tau_{\gamma \delta}^{a} C_{\alpha}^{+}(r) C_{\beta}(r) C_{\gamma}^{+}(r) C_{\delta}(r)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{4} (2 \delta_{\alpha \delta} \delta_{\beta \gamma} - \delta_{\alpha \beta} \delta_{\delta \gamma}) C_{\alpha}^{+}(r) C_{\beta}(r) C_{\gamma}^{+}(r) C_{\delta}(r) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2} C_{\alpha}^{+} C_{\beta} C_{\beta}^{+} C_{\alpha} - \frac{1}{4} C_{\alpha}^{+} C_{\alpha} C_{\beta}^{+} C_{\beta} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2} C_{\uparrow}^{+} (C_{\uparrow} C_{\uparrow}^{+} + C_{\downarrow} C_{\downarrow}^{+}) C_{\uparrow} + \frac{1}{2} C_{\downarrow}^{+} (C_{\uparrow} C_{\uparrow}^{+} + C_{\downarrow} C_{\downarrow}^{+}) C_{\downarrow} - \frac{1}{4} (C_{\uparrow}^{+} C_{\uparrow} + C_{\downarrow}^{+} C_{\downarrow}) (C_{\uparrow}^{+} C_{\uparrow} + C_{\downarrow}^{+} C_{\downarrow}) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} + \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow} C_{\downarrow}^{+} + \frac{1}{2} C_{\downarrow}^{+} C_{\downarrow} C_{\uparrow} C_{\uparrow}^{+} + \frac{1}{2} C_{\downarrow}^{+} C_{\downarrow} - \frac{1}{4} (C_{\uparrow}^{+} C_{\uparrow} + 2 C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} + C_{\downarrow}^{+} C_{\downarrow} )}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} + \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} - \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} + \frac{1}{2} C_{\downarrow}^{+} C_{\downarrow} - \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} + \frac{1}{2} C_{\downarrow}^{+} C_{\downarrow} - \frac{1}{4} C_{\uparrow}^{+} C_{\uparrow} - \frac{1}{4} C_{\downarrow}^{+} C_{\downarrow} - \frac{1}{2} C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{3}{4} (C_{\uparrow}^{+} C_{\uparrow} + C_{\downarrow}^{+} C_{\downarrow}) - \frac{3}{2} C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} }
so
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\uparrow}^{+} C_{\uparrow} C_{\downarrow}^{+} C_{\downarrow} = - \frac{2}{3} S^2 + \frac{1}{2} (C_{\uparrow}^{+} C_{\uparrow} + C_{\downarrow}^{+} C_{\downarrow}) }
The interaction part of the Hamiltonian now becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{int} = - \frac{2}{3} u \sum_{r} \vec{S}(r) \cdot \vec{S}(r) + \frac{1}{2} u \sum_{r, \sigma} C_{\sigma}^{+}(r) C_{\sigma}(r) }
from which it is clear that H has SU(2) symmetry.
To write the coherent state path integral for the system, its Hamiltonian should be expressed in normal order
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S} \cdot \vec{S} = \frac{1}{4} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} C_{\beta} C_{\gamma}^{+} \vec{\tau}_{\gamma \delta} C_{\delta} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{4} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} ( [C_{\beta}, C_{\gamma}^{+}]_{-} - C_{\gamma}^{+} C_{\delta}) \vec{\tau}_{\gamma \delta} C_{\delta} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{3}{4} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} \cdot \vec{\tau}_{\beta \delta} C_{\delta} - \frac{1}{4} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} C_{\gamma}^{+} C_{\beta} \vec{\tau}_{\beta \delta} C_{\delta} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{3}{4} C_{\alpha}^{+} C_{\alpha} - \frac{1}{4} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} C_{\gamma}^{+} C_{\beta} \vec{\tau}_{\beta \delta} C_{\delta} }
Hence
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{int} = ( - \frac{u}{2} + \frac{u}{2} ) \sum_{r, \sigma} C_{\sigma}^{+}(r) C_{\sigma}(r) -\frac{2}{3} u \sum_{r} (- \frac{1}{4}) C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} C_{\gamma}^{+} C_{\beta} \vec{\tau}_{\beta \delta} C_{\delta} = \frac{1}{6} \sum_{r} C_{\alpha}^{+} \vec{\tau}_{\alpha \beta} C_{\gamma}^{+} C_{\beta} \vec{\tau}_{\beta \delta} C_{\delta}}
Now the path integral for the system is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int D[\psi_{\sigma}^{*}, \psi_{\sigma}] e^{- \int_{0}^{\beta} \sum_{r} L } }
where the Lagrangian is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = \psi_{\sigma}^{*}(r, \tau) (\frac{\partial}{\partial \tau} - \mu) \psi_{\sigma}(r, \tau) - t \sum_{\delta} [ \psi_{\sigma}^{*}(r, \tau) \psi_{\sigma}(r+ \delta, \tau) + \psi_{\sigma}^{*}(r + \delta, \tau) \psi_{\sigma}(r, \tau) ] - \frac{u}{6} [ \psi_{\alpha}^{*}(r, \tau) \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau) ]^2 }
To deal with the quartic interaction term, we use the Hubbard-Stratonovic transformation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ \frac{u}{6} [\psi_{\alpha}^{*}(r, \tau) \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau)]^2 d \tau } = const \cdot \int d \phi_x d \phi_y d \phi_z e^{- \frac{1}{2} \vec{\phi} \cdot \vec{\phi} d \tau} e^{\lambda \vec{\phi} \cdot [\psi_{\alpha}^{*}(r, \tau) \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau)] d \tau } }
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\eta} = \psi_{\alpha}^{*}(r, \tau) \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau) } , then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \frac{1}{2} \vec{\phi} \cdot \vec{\phi} d \tau + \lambda \vec{\phi} \cdot \vec{\eta} d \tau = - \frac{1}{2} (\vec{\phi} - \lambda \vec{\eta})^2 d \tau + \frac{1}{2} \lambda^2 \vec{\eta}^2 d \tau }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda = - \sqrt{u/3} } . Hence
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ \frac{u}{6} [\psi_{\alpha}^{*}(r, \tau) \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau)]^2 d \tau } = const \cdot ( \int d \phi_x d \phi_y d \phi_z e^{- \frac{1}{2} \vec{\phi}^2 d \tau} ) e^{\frac{\lambda^2}{2} \vec{\eta}^2 d \tau} }
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{int} = \sqrt{\frac{u}{3}} \vec{\phi}(r, \tau) \cdot \psi_{\alpha}^{*} \vec{\tau}_{\alpha \beta} \psi_{\beta}(r, \tau) + \frac{1}{2} [\vec{\phi}(r, \tau)]^2 }
Now the partition function of the system is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z = const \cdot \int D[\phi] \int D[\psi_{\alpha}^{*}, \psi_{\alpha}] e^{- \int_{0}^{\beta} d \tau \sum_{r} (L_o + L_{int})} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = const \cdot \int D[\phi] e^{- \int_{0}^{\beta} d \tau \sum_{r} \frac{1}{2} [\vec{\phi}(r, \tau)]^2} \cdot Det[(\frac{\partial}{\partial \tau} - \mu + \hat{h}_o)_{\alpha \beta} + \sqrt{\frac{u}{3}} \vec{\phi}(r, \tau) \cdot \vec{\tau}_{\alpha \beta} ]}
Furthermore, define
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{- \frac{1}{2} \int_{\tau} \sum_{r} \phi^2} e^{ln Det[...]} = e^{- S_{eff}[\vec{\phi}]} }
Applying the saddle-point approximation we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 = \frac{\delta S_{eff}(\vec{\phi})}{\delta \phi_{\alpha}(r, \tau)} = - \phi_{\alpha}^{(s)}(r, \tau) + \frac{\delta}{\delta \phi_{\alpha (r, \tau)}} Tr[ln[(\frac{\partial}{\partial \tau} - \mu + \hat{h}_o)_{\alpha \beta} + \sqrt{\frac{u}{3}} \vec{\phi}(r, \tau) \cdot \vec{\tau}_{\alpha \beta}]] }
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\alpha}^{(s)}(r, \tau) = Tr [[(\frac{\partial}{\partial \tau} - \mu + \hat{h}_o)_{ij} + \sqrt{\frac{u}{3}} \phi^{(s)}(r', \tau') \cdot \vec{\tau}_{ij}]_{\alpha \beta}^{-1} \sqrt{\frac{u}{3}} \tau_{\alpha \beta}^a \delta(r-r') \delta(\tau - \tau')] }
Two-dimensional Hubbard Hamiltonian in Momentum Space
The Hamiltonian for the Hubbard model can be expressed in reciprocal space by performing a Fourier transformation of the real space Hamiltonian. This can be done by writing the creation and annihilation operators in terms of their Fourier series:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\sigma}(m,n) = \frac{1}{\sqrt{n_{x}n_{y}}}\sum_{k_{x},k_{y}}C_{\sigma}(k_{x},k_{y})e^{i k_{x}m}e^{i k_{y}n} } .
And likewise,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\sigma}^{\dagger}(m,n) = \frac{1}{\sqrt{n_{x}n_{y}}}\sum_{k_{x},k_{y}}C_{\sigma}^{\dagger}(k_{x},k_{y})e^{-i k_{x}m}e^{-i k_{y}n} } ,
where, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} are the discrete lattice site positions, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{x}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{y}} are the number of sites in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} directions, respectively, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{x}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{y}} are the reciprocal space components to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} . The total number of sites is then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M=n_{x}n_{y}} .
The Hamiltonian including both the direct hopping and interaction terms is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -t \sum_{m,n}\sum_{m',n'} \sum_{\sigma = \uparrow \downarrow} [C_{\sigma}^{\dagger}(m,n) C_{\sigma}(m',n') + C_{\sigma}^{\dagger}(m',n') C_{\sigma}(m,n)] + U \sum_{m,n}^{} C_{\uparrow}^{\dagger}(m,n) C_{\downarrow}^{\dagger}(m,n) C_{\downarrow}(m,n) C_{\uparrow}(m,n) }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m'} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n'} can only be one lattice spacing away from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} .
Substituting in the Fourier series for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\sigma}^{\dagger}(m,n)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\sigma}^{}(m,n)} , the resulting Hamiltonian is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{hopping} = -t \sum_{m,n}\sum_{m',n'} \sum_{\sigma = \uparrow \downarrow} \Big [ \sum_{k_{x},k_{y}}C_{\sigma}^{\dagger}(k_{x},k_{y})e^{-i k_{x}m}e^{-i k_{y}n} \sum_{p_{x},p_{y}}C_{\sigma}(p_{x},p_{y})e^{i p_{x}m'}e^{i p_{y}n'} + \sum_{k_{x},k_{y}}C_{\sigma}^{\dagger}(k_{x},k_{y})e^{-i k_{x}m'}e^{-i k_{y}n'} \sum_{k_{x},k_{y}}C_{\sigma}(p_{x},p_{y})e^{i p_{x}m}e^{i p_{y}n} \Big]}
Since there is only direct hopping, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m'=m+\lambda } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n'=n+\lambda'} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=\pm 1} when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda'=0} and vise-versa.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{hopping} = -t \sum_{m,n}\sum_{\lambda,\lambda'} \sum_{\sigma = \uparrow \downarrow} \bigg[\frac{1}{M}\sum_{k_{x},k_{y}}\sum_{p_{x},p_{y}}e^{i(p_{x}-k_{x})m}e^{i(p_{y}-k_{y})n}C_{\sigma}^{\dagger}(k_{x},k_{y}) C_{\sigma}(p_{x},p_{y})e^{i p_{x}\lambda}e^{i p_{y}\lambda'} + \frac{1}{M}\sum_{k_{x},k_{y}}\sum_{p_{x},p_{y}}e^{i (p_{y}-k_{x})m}e^{i (p_{y}-k_{y})n}C_{\sigma}^{\dagger}(k_{x},k_{y})C_{\sigma}(p_{x},p_{y})e^{-i p_{x}\lambda}e^{-i p_{y}\lambda'}\bigg]}
However, the sums over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} create delta-functions:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{m,n}e^{i (p_{y}-k_{x})m}e^{i (p_{y}-k_{y})n}=M \delta_{p_{x},k_{x}} \delta_{p_{y},k_{y}}}
therefore, the hopping term becomes:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} H_{hopping} &= -t \sum_{k_{x},k_{y}}\sum_{\lambda,\lambda'} \sum_{\sigma\uparrow\downarrow}[C_{\sigma}^{\dagger}(k_{x},k_{y})C_{\sigma}(k_{x},k_{y})e^{i k_{x}\lambda}e^{i k_{y}\lambda'} + C_{\sigma}^{\dagger}(k_{x},k_{y})C_{\sigma}(k_{x},k_{y})e^{-i k_{x}\lambda}e^{-i k_{y}\lambda'}]\\ &= -2t \sum_{k_{x},k_{y}} \sum_{\sigma = \uparrow \downarrow}(cos(k_{x})+cos(k_{y}))C_{\sigma}^{\dagger}(k_{x},k_{y})C_{\sigma}(k_{x},k_{y}) \\ &= -2t\sum_{\sigma = \uparrow \downarrow}\sum_{k_{x},k_{y}}(cos(k_{x})+cos(k_{y}))n_{\sigma}(k_{x},k_{y}) \\ &= -4t\sum_{k_{x},k_{y}}(cos(k_{x})+cos(k_{y}))n(k_{x},k_{y})\end{align} }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n(k_{x},k_{y})} is the number operator for the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (k_{x},k{y})} .
Likewise, for the interaction term,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{int} = \frac{U}{M^{2}} \sum_{m,n}^{} C_{\uparrow}^{\dagger}(m,n) C_{\downarrow}^{\dagger}(m,n) C_{\downarrow}(m,n) C_{\uparrow}(m,n) } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{U}{M^{2}} \sum_{m,n}^{} \sum_{k_{1,x},k_{1,y}}C_{\uparrow}^{\dagger}(k_{1,x},k_{1,y})e^{-i k_{1,x}m}e^{-i k_{1,y}n}\sum_{k_{2,x},k_{2,y}}C_{\downarrow}^{\dagger}(k_{2,x},k_{2,y})e^{-i k_{2,x}m}e^{-i k_{2,y}n}\sum_{k_{3,x},k_{3,y}}C_{\downarrow}(k_{3,x},k_{3,y})e^{i k_{3,x}m}e^{i k_{3,y}n}\sum_{k_{4,x},k_{4,y}}C_{\uparrow}(k_{4,x},k_{4,y})e^{i k_{4,x}m}e^{i k_{4,y}n} }
Implementing the delta-functions again and defining Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{k}=(k_{x},k_{y})} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{k_{1}}-\bold{k_{4}}=\bold{k_{3}-\bold{k_{2}}}} .
This relation can be satisfied by defining Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{q}} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{k_{1}}=\bold{k}, \bold{k_{4}}=\bold{k}-\bold{q}, \bold{k_{2}}=\bold{k}', \bold{k_{3}}=\bold{k}'+\bold{q}} .
And so,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{int} = \frac{U}{M}\sum_{\bold{k},\bold{k}',\bold{q}}C_{\uparrow}^{\dagger}(\bold{k})C_{\downarrow}^{\dagger}(\bold{k}')C_{\downarrow}(\bold{k}'+\bold{q})C_{\uparrow}(\bold{k}-\bold{q})}
The total Hamiltonian in reciprocal space is then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=H_{hopping}+H_{int}=-4t\sum_{k_{x},k_{y}}(cos(k_{x})+cos(k_{y}))n(k_{x},k_{y})+\frac{U}{M}\sum_{\bold{k},\bold{k}',\bold{q}}C_{\uparrow}^{\dagger}(\bold{k})C_{\downarrow}^{\dagger}(\bold{k}')C_{\downarrow}(\bold{k}'+\bold{q})C_{\uparrow}(\bold{k}-\bold{q})} .
Calculation of the 2D Grand Canonical Potential
The grand canonical potential, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} , is best calculated by using coherent state path integral. The grand partition function is defined as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z = Tr \big[e^{-\beta (H - \mu N)} \big] = e^{-\beta \Omega} }
which can be expanded as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z = Z_{0} \big\langle e^{-S_{int}} \big\rangle = Z_{0} e^{-\langle S_{int} \rangle} e^{\frac{1}{2}( \langle S_{int}^2 \rangle - \langle S_{int} \rangle^2)} = e^{-\beta \Omega_0}e^{-\beta \Omega_1}e^{-\beta \Omega_2} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{int} = \int_{0}^{\beta} d\tau H_{int} (\tau) }
which utilizes cumulant expansion. We begin to calculate the grand canonical potential by analyzing the contribution from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_0 } :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{0} = \prod_k (1+e^{-\beta(E_k - \mu)})^2 = e^{2 \sum_k ln(1+e^{-\beta(E_k - \mu)})} = e^{-\beta \Omega_0} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_0 = -\frac{2}{\beta} \sum_k ln(1+e^{-\beta(E_k - \mu)}) }
Now we look at the contribution from the first order cumulant expansion.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle S_{int} \rangle = \bigg \langle \int_{0}^{\beta} d\tau \frac{U}{M} \sum_{k,k',q} C_{k,\uparrow}^{\dagger}(\tau) C_{k',\downarrow}^{\dagger}(\tau) C_{k'+q,\downarrow}(\tau) C_{k-q,\uparrow}(\tau) \bigg \rangle }
The only contraction combination possible, due to orthogonal spins, results in the following set of Green's functions:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \langle S_{int} \rangle &= \int_{0}^{\beta} d\tau \frac{U}{M} \sum_{k,k'} \big \langle \mathcal{G}_{0}(k\tau,k\tau)\mathcal{G}_{0}(k'\tau,k'\tau) \big \rangle \\ &= \int_{0}^{\beta} d\tau \frac{U}{M} \sum_{k,k'} n_{F}(\epsilon_{k}) n_{F}(\epsilon_{k'}) \\ &= {\beta} \frac{U}{M} \sum_{k,k'} n_{F}(\epsilon_{k}) n_{F}(\epsilon_{k'}) = \beta \Omega_1 \end{align} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_1 = \frac{U}{M} \sum_{k,k'} n_{F}^2(\epsilon_k) }
Combining both terms, the grand canonical potential to first order is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega = \Omega_0 + \Omega_1 = -\frac{2}{\beta} \sum_k ln(1+e^{-\beta(E_k - \mu)}) + \frac{U}{M} \sum_{k} n_{F}^2(\epsilon_k) }
Calculation of the 2D Chemical Potential
The Grand Canonical Potential for a 2-D lattice is defined as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega = -\frac{2}{\beta} \sum_{k}^{} ln(1 + e^{\beta (E_{k}-\mu)})+ \frac{U}{M} (\sum_k \frac{1}{e^{\beta (E_{k}-\mu)}+1)})^2 }
In the grand canonical scheme, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_f = - \frac{\partial{\Omega}}{\partial{\mu}} }
The interaction induced correction to the chemical potential, δµ, can be found in first order U.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -N_f = - \frac{2}{\beta} \sum_{k} \frac{\beta e^{-\beta(E_k-\mu)}}{e^{-\beta(E_k-\mu)}+1}+2 \frac{U}{M} (\sum_{k} \frac{1}{e^{\beta (E_{k}-\mu)}+1}) \sum_{k'} \frac{\beta e^{\beta (E_{k'}-\mu)}}{(e^{\beta (E_{k'}-\mu)}+1)^2} }
Using the definition, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu=\mu_o + \delta\mu } , and expanding Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -2 \sum_{k} n_f(E_k-\mu_o-\delta\mu) -2\frac{U}{M}\sum_{k} n_f(E_k-\mu_o) \sum_{k'} n_f(E_{k'}-\mu_o) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \simeq -2 \sum_{k} n_f(E_k-\mu_o) + 2\delta\mu \sum_{k'} n_f(E_{k'}-\mu_o)-2 \frac{U}{M}\sum_{k} n_f(E_k-\mu_o) \sum_{k'} n_f(E_{k'}-\mu_o) }
By definition,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_f = 2 \sum_{k} n_f \left (E_k - \mu_o \right) }
As a result, solving for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta\mu }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta\mu = \frac{1}{2} U \frac{N_f}{M} ; \mu = \mu_o +\frac{1}{2} U \frac{N_f}{M} + O(U^2) }
Alternativey, consider
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \hat{H}-\mu \hat{N} &= -t \sum_{\sigma}\sum_{m=1}^{\frac{n_x}{2}}\sum_{n=1}^{\frac{n_y}{2}}(A_{2m,2n,\sigma}^{\dagger}B_{2m+1,2n,\sigma}+A_{2m,2n,\sigma}^{\dagger}B_{2m- 1,2n,\sigma}+A_{2m,2n,\sigma}^{\dagger}B_{2m,2n+1,\sigma}+A_{2m,2n,\sigma}^{\dagger}B_{2m,2n-1,\sigma}+h.c) \\ &+ U\sum_{m=1}^{\frac{n_x}{2}}\sum_{n=1}^{\frac{n_y}{2}} (A_{2m,2n,\uparrow}^{\dagger}A_{2m,2n,\downarrow}^{\dagger}A_{2m,2n,\downarrow}A_{2m,2n,\uparrow} +B_{2m+1,2n+1,\uparrow}^{\dagger}B_{2m+1,2n+1,\downarrow}^{\dagger}B_{2m+1,2n+1,\downarrow}B_{2m+1,2n+1,\uparrow}) \\ &- \mu\sum_{\sigma}\sum_{m=1}^{\frac{n_x}{2}}\sum_{n=1}^{\frac{n_y}{2}}(A_{2m,2n,\sigma}^{\dagger}A_{2m,2n,\sigma}+B_{2m+1,2n+1,\sigma}^{\dagger}B_{2m+1,2n+1,\sigma}) \end{align}}
The condition for half-filling, or one electron per site is given by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\sigma} \langle A_{2m,2n,\sigma}^{\dagger}A_{2m,2n,\sigma} \rangle = 1}
The grand canonical potential is invariant under the particle hole transformation for half filling, that is: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = d^{\dagger}; B = -f^{\dagger}; A^{\dagger} = d; B^{\dagger} = -f}
where d and f obey the commutation relations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [f,f{\dagger}]=1; [d,d{\dagger}]=1}
A short digression into the nature of f and d reveals that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\sigma} \langle d_{2m,2n,\sigma}d_{2m,2n,\sigma}^{\dagger} \rangle = 1 }
Using the commutation relations, this shows the grand canonical potential to be invariant under particle hole transformation
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1- \langle d_{2m,2n,\uparrow}^{\dagger}d_{2m,2n,\uparrow} \rangle + 1 - \langle d_{2m,2n,\downarrow}^{\dagger}d_{2m,2n,\downarrow} \rangle = 1 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle d_{2m,2n,\uparrow}^{\dagger}d_{2m,2n,\uparrow} \rangle + \langle d_{2m,2n,\downarrow}^{\dagger}d_{2m,2n,\downarrow} \rangle = 1}
This recovers the half filling condition for a particle hole transformation.
Substituting d and f into the Hamiltonian and using the commutation relations to create an analogue to the original Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}-\mu\hat{N}} , it is evident that when comparing
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\left(t,\mu,U\right)=H\left(t,\mu,-\mu+U\right)}
Under such a transformation, it is clear that the chemical potential is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\mu+U=-\mu \Rightarrow \mu=\frac{U}{2} }
This recovers the condition for half-filling from above since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M = N_{f} }
Isothermal Compressibility
In the limit of low temperature, the isothermal compressibility,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa_{T}} which satisfies the relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa_{T}\rho^{2}=\frac{\partial\rho}{\partial\mu}} , can be corrected as a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_{0}} to first order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=\frac{N_{F}}{M}}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{F}=\sum_{\bold{k}}n_{F}(E_{\bold{k}}-\mu)+2\frac{U}{M}\sum_{\bold{k}}n_{F}(E_{\bold{k}}-\mu)\sum_{\bold{k}'}\frac{\partial n_{F}(E_{\bold{k}'}-\mu)}{\partial\mu}}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{F}} is the Fermi-Dirac distribution function.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial N_{F}}{\partial \mu}=-2\sum_{\bold{k}}n_{F}'(E_{\bold{k}}-\mu)-2\frac{U}{M}(\sum_{\bold{k}}n_{F}'(E_{\bold{k}}-\mu))^{2}-2\frac{U}{M}\sum_{\bold{k}}n_{F}(E_{\bold{k}}-\mu)\sum_{\bold{k}'}n_{F}''(E_{\bold{k}'}-\mu)}
where the primes on the distribution functions denote derivatives with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} .
Setting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu=\mu_{0}+\delta\mu} and expanding around Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta\mu} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial N_{F}}{\partial \mu}\simeq-2\sum_{\bold{k}}n_{F}'(E_{\bold{k}}-\mu_{0})+2\delta\mu\sum_{\bold{k}}n_{F}''(E_{\bold{k}}-\mu_{0})-2\frac{U}{M}(\sum_{\bold{k}}n_{F}'(E_{\bold{k}}-\mu_{0}))^{2}+\frac{U}{M}N_{F}\sum_{\bold{k}}n_{F}''(E_{\bold{k}}-\mu_{0})+O(U^{2})} .
Setting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta\mu=\frac{UN_{F}}{2M}} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial N_{F}}{\partial \mu}\simeq(-2\sum_{\bold{k}}n_{F}'(E_{\bold{k}}-\mu_{0}))(1+\frac{U}{M}\sum_{\bold{k}'}n_{F}'(E_{\bold{k}'}-\mu_{0}))} .
The above expression can be written in terms of the density of states, and taking Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T=0} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{M}\frac{\partial N_{F}}{\partial\mu}=\frac{\partial\rho}{\partial\mu}=2N(\mu_{0})(1-U N(\mu_{0}))=\rho^{2}\kappa_{T}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\mu_{0})} is the density of states at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa_{T}=\frac{2N(\mu_{0})(1-U N(\mu_{0}))}{\rho^{-2}}} .
Mean Field Theory and its relation to the Saddle Point Approximation
We may relate the above calculation of the saddle point for the path integral to the concept of broken symmetry. Before we do so, however, we will introduce mean field theory, which, as it will turn out, is related to the saddle point approximation. Our discussion of mean field theory will follow that found in Fradkin's book (E. Fradkin, Field Theories of Condensed Matter Physics, Westview Press (1998)), though some of our definitions differ from his. We will illustrate the basic idea of mean field theory using the Hubbard model written in terms of the spin operator, which we repeat here.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=-t\sum_{\langle\vec{r}\vec{r}'\rangle,\sigma}[c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r}')+\text{h.c.}]+\tfrac{1}{2}U\sum_{\vec{r},\sigma}c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r})-\tfrac{2}{3}U\sum_{\vec{r}}\vec{S}(\vec{r})\cdot\vec{S}(\vec{r})}
Throughout this section, we will be working in two dimensions, and at zero temperature.
The mean field approximation we will use is as follows. We first rewrite the spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(\vec{r})} in the Hamiltonian as a sum of its expectation value plus its deviation from said expectation value (the fluctuation term),
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(\vec{r})=\langle\vec{S}(\vec{r})\rangle+[\vec{S}(\vec{r})-\langle\vec{S}(\vec{r})\rangle],}
obtaining
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=-t\sum_{\langle\vec{r}\vec{r}'\rangle,\sigma}[c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r}')+\text{h.c.}]+\tfrac{1}{2}U\sum_{\vec{r},\sigma}c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r})-\tfrac{2}{3}U\sum_{\vec{r}}\langle\vec{S}(\vec{r})\rangle\cdot\langle\vec{S}(\vec{r})\rangle-\tfrac{4}{3}U\sum_{\vec{r}}\langle\vec{S}(\vec{r})\rangle\cdot[\vec{S}(\vec{r})-\langle\vec{S}(\vec{r})\rangle]-\tfrac{2}{3}U\sum_{\vec{r}}[\vec{S}(\vec{r})-\langle\vec{S}(\vec{r})\rangle]\cdot[\vec{S}(\vec{r})-\langle\vec{S}(\vec{r})\rangle].}
Finally, we drop the last term, which is quadratic in the fluctuations, thus obtaining the mean field Hamiltonian,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}=-t\sum_{\langle\vec{r}\vec{r}'\rangle,\sigma}[c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r}')+\text{h.c.}]+\tfrac{1}{2}U\sum_{\vec{r},\sigma}c_{\sigma}^{\dagger}(\vec{r})c_{\sigma}(\vec{r})-\tfrac{4}{3}U\sum_{\vec{r}}\vec{M}(\vec{r})\cdot\vec{S}(\vec{r})+\tfrac{2}{3}U\sum_{\vec{r}}\vec{M}(\vec{r})\cdot\vec{M}(\vec{r}),}
where we define
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})=\langle\vec{S}(\vec{r})\rangle.}
From this point on, we will treat Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} as a parameter. Note that this Hamiltonian, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} is not zero, breaks the SU(2) symmetry of the original Hubbard model due to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})\cdot\vec{S}(\vec{r})} term.
We will now rewrite this Hamiltonian in momentum space. If we introduce the Fourier transform of the creation and annihilation operators,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{\sigma}(\vec{r})=\frac{1}{\sqrt{N}}\sum_{\vec{k}}c_{\sigma}(\vec{k})e^{i\vec{k}\cdot\vec{r}},}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} is the number of sites, then the non-interacting part of the Hamiltonian will be diagonalized:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0=\sum_{\vec{k},\sigma}\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k}),}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})=-2t(\cos{k_x a}+\cos{k_y a}).}
We will assume that these operators are periodic, in that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{\sigma}(\vec{k})} is the same as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{\sigma}(\vec{k}+\vec{G})} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{G}} is a reciprocal lattice vector.
If we perform a similar transformation on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})=\frac{1}{N}\sum_{\vec{k}}\vec{M}(\vec{k})e^{i\vec{k}\cdot\vec{r}},}
and similarly for the spin operator, we get, for the interaction part of the Hamiltonian,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\vec{r}}\vec{M}(\vec{r})\cdot\vec{S}(\vec{r})=\frac{1}{N^2}\sum_{\vec{k}\vec{k}'}\sum_{\vec{r}}\vec{M}(\vec{k}')\cdot\vec{S}(\vec{k})e^{i(\vec{k}+\vec{k}')\cdot\vec{r}}=\frac{1}{N}\sum_{\vec{k}}\vec{M}(\vec{-k})\cdot\vec{S}(\vec{k})=\frac{1}{N}\sum_{\vec{k}}\vec{M}^{\ast}(\vec{k})\cdot\vec{S}(\vec{k})}
In the last step, we used the fact that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} is real. Similarly,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\vec{r}}\vec{M}(\vec{r})\cdot\vec{M}(\vec{r})=\frac{1}{N}\sum_{\vec{k}}\vec{M}^{\ast}(\vec{k})\cdot\vec{M}(\vec{k}).}
We will also want to know Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(\vec{k})} in terms of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{\sigma}(\vec{k}).}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(\vec{k})=\sum_{\vec{r}}\vec{S}(\vec{r})e^{-i\vec{k}\cdot\vec{r}}=\tfrac{1}{2}\sum_{\vec{r},\alpha\beta}c_{\alpha}^{\dagger}(\vec{r})\tau_{\alpha\beta}c_{\beta}(\vec{r})e^{-i\vec{k}\cdot\vec{r}}=\frac{1}{2N}\sum_{\vec{k}'\vec{k}'',\alpha\beta}\sum_{\vec{r}}c_{\alpha}^{\dagger}(\vec{k}')\tau_{\alpha\beta}c_{\beta}(\vec{k}'')e^{i(\vec{k}''-\vec{k}'-\vec{k})\cdot\vec{r}}=\tfrac{1}{2}\sum_{\vec{k}',\alpha\beta}c_{\alpha}^{\dagger}(\vec{k}')\tau_{\alpha\beta}c_{\beta}(\vec{k}+\vec{k}')}
Putting everything together, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}=\sum_{\vec{k},\sigma}\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})+\tfrac{1}{2}U\sum_{\vec{k},\sigma}c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})-\frac{2U}{3N}\sum_{\vec{k}\vec{k}',\alpha\beta}\vec{M}^{\ast}(\vec{k})\cdot c_{\alpha}^{\dagger}(\vec{k}')\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}+\vec{k}')+\frac{2U}{3N}\sum_{\vec{k}}\vec{M}^{\ast}(\vec{k})\cdot\vec{M}(\vec{k}).}
Let us now assume that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} has a specific form, namely
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})=\vec{M}_0\cos(\vec{Q}\cdot\vec{r}),}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{Q}=\left (\tfrac{\pi}{a},\tfrac{\pi}{a}\right ),}
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})=\tfrac{1}{2}\vec{M}_0(e^{i\vec{Q}\cdot\vec{r}}+e^{-i\vec{Q}\cdot\vec{r}}).}
This would correspond to an antiferromagnetic ordering. The only two non-zero Fourier components of this vector are
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{Q})=\vec{M}(-\vec{Q})=\tfrac{1}{2}N\vec{M}_0,}
so that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}=\sum_{\vec{k},\sigma}\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})+\tfrac{1}{2}U\sum_{\vec{k},\sigma}c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}+\vec{Q})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}-\vec{Q})+\tfrac{1}{3}NU|\vec{M}_0|^2.}
From this point forward, we will work at half-filling. That is, we will introduce a chemical potential term,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\mu\sum_{\vec{k},\sigma}c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k}),}
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu=\tfrac{1}{2}U,} so that the second term is canceled out. It can be shown that, at half-filling, the Hubbard model becomes antiferromagnetic in two dimensions, as we are assuming here. The Hamiltonian is now just
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}=\sum_{\vec{k},\sigma}\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}+\vec{Q})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}-\vec{Q})+\tfrac{1}{3}NU|\vec{M}_0|^2.}
We will now diagonalize this Hamiltonian. To do so, we will make use of the periodicity of the lattice to reduce the third term to the Hermitian adjoint of the second. We note that the vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{Q}} is exactly half of a reciprocal lattice vector. Therefore, if we add Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\vec{Q}} to all wave vectors in the third term, it becomes the Hermitian adjoint of the second:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}=\sum_{\vec{k},\sigma}\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}+\vec{Q})-\tfrac{1}{3}U\sum_{\vec{k},\alpha\beta}\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k}+\vec{Q})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k})+\tfrac{1}{3}NU|\vec{M}_0|^2.}
We may split the first term into two terms, each over half of the Brillouin zone. We may do the same for the next two terms as well. If we use the "nesting" property,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k}+\vec{Q})=-2t[\cos(k_x a+\pi)+\cos(k_y a+\pi)]=2t(\cos{k_x a}+\cos{k_y a})=-\epsilon(\vec{k}),}
we may rewrite the above as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{MF}={\sum_{\vec{k},\sigma}}'\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k})c_{\sigma}(\vec{k})-{\sum_{\vec{k},\sigma}}'\epsilon(\vec{k})c_{\sigma}^{\dagger}(\vec{k}+\vec{Q})c_{\sigma}(\vec{k}+\vec{Q})-\tfrac{2}{3}U{\sum_{\vec{k},\alpha\beta}}'\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k}+\vec{Q})-\tfrac{2}{3}U{\sum_{\vec{k},\alpha\beta}}'\vec{M}_0\cdot c_{\alpha}^{\dagger}(\vec{k}+\vec{Q})\vec{\tau}_{\alpha\beta}c_{\beta}(\vec{k})+\tfrac{1}{3}NU|\vec{M}_0|^2,}
where a prime on a sum means that the wave vectors are only summed over the upper half (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_y>0} ) of the Brillouin zone.
To diagonalize this Hamiltonian, we will write it in matrix form. Each term in the sum can be written in the form,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi^{\dagger}(\vec{k})\mathcal{H}(\vec{k})\Psi(\vec{k}),}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(\vec{k})=\left [\begin{array}{c} c_{\uparrow}(\vec{k}) \\ c_{\downarrow}(\vec{k}) \\ c_{\uparrow}(\vec{k}+\vec{Q}) \\ c_{\downarrow}(\vec{k}+\vec{Q}) \end{array}\right ]}
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}(\vec{k})=\left [\begin{array}{cc} \epsilon(\vec{k}) & -\tfrac{2}{3}U\vec{M}_0\cdot\vec{\tau} \\ -\tfrac{2}{3}U\vec{M}_0\cdot\vec{\tau} & -\epsilon(\vec{k}) \end{array}\right ],}
where each entry represents a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\times 2} block. If we square the above matrix, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\mathcal{H}(\vec{k})]^2=\left [\begin{array}{cc} [\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2 & 0 \\ 0 & [\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2 \end{array}\right ].}
We therefore see that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}(\vec{k})} possesses two eigenvalues, given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\pm}(\vec{k})=\pm\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}.}
The spectrum therefore has a gap, with magnitude Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{4}{3}U|\vec{M}_0|.}
We may see that these represent states of definite projection of spin along Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0} . Let us suppose that we chose to quantize the spin of our electrons along Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0} , or, equivalently, we chose our coordinates so that, say, the z-axis was along Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0} . Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}(\vec{k})} becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}(\vec{k})=\left [\begin{array}{cccc} \epsilon(\vec{k}) & 0 & -\tfrac{2}{3}UM_0 & 0 \\ 0 & \epsilon(\vec{k}) & 0 & \tfrac{2}{3}UM_0 \\ -\tfrac{2}{3}UM_0 & 0 & -\epsilon(\vec{k}) & 0 \\ 0 & \tfrac{2}{3}UM_0 & 0 & -\epsilon(\vec{k}) \\ \end{array}\right ].}
This matrix can easily be reduced to block diagonal form, and it only mixes operators that create particles with the same spin (that is, it only mixes a spin up state with another spin up state, for example). We also find that the above energies, in fact, form doubly degenerate pairs, each corresponding to a spin up or a spin down state. We may then obtain the result for any relative orientation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0} to the spin quantization axis via the appropriate SU(2) transformation applied to each pair of operators in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(\vec{k})} at the same wave vector.
Now that we know the energies, we may now write down the energy of the ground state of our system. The ground state is simply the state in which all of the negative energy single-particle states are occupied. It also has zero average spin because we occupy an equal number of spin up and spin down states. Its energy is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{GS}=-2{\sum_{\vec{k}}}'E_{+}(\vec{k})+\tfrac{1}{3}NU|\vec{M}_0|^2=-2{\sum_{\vec{k}}}'\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}+\tfrac{1}{3}NU|\vec{M}_0|^2.}
We will now need to minimize this energy with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0.} We are essentially applying the variational principle, using Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0} as a parameter. We require that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0=\frac{\partial E_{GS}}{\partial M_{0,i}}=-2{\sum_{\vec{k}}}'\frac{\tfrac{4}{9}U^2 M_{0,i}}{\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}+\tfrac{2}{3}NUM_{0,i}.}
Rearranging the above equation, we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\sum_{\vec{k}}}'\frac{M_{0,i}}{\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3N}{U}M_{0,i}.}
There are two possible solutions. One of these is to simply set all of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{0,i}=0,} which corresponds to a paramagnetic state. The other is given by
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\sum_{\vec{k}}}'\frac{1}{\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3N}{U}.}
Notice that the above equation only involves the magnitude of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}_0.} This means that the direction may be chosen arbitrarily.
Let us now take the thermodynamic limit. In this case, the sum on the left-hand side becomes an integral:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Na^2 \int_{-\pi/a}^{\pi/a}\frac{dk_x}{2\pi}\int_{0}^{\pi/a}\frac{dk_y}{2\pi}\,\frac{1}{\sqrt{[\epsilon(\vec{k})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3N}{U}.}
If we change variables to the dimensionless quantities, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \kappa_{i}=k_{i}a} , we obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\pi}^{\pi}\frac{d\kappa_x}{2\pi}\int_{0}^{\pi}\frac{d\kappa_y}{2\pi}\,\frac{1}{\sqrt{[\epsilon(\vec{\kappa})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3}{U}.}
Using the fact that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \epsilon(-\kappa_x,\kappa_y)=\epsilon(\kappa_x,\kappa_y),} we may write
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{\pi}\frac{d\kappa_x}{2\pi}\int_{0}^{\pi}\frac{d\kappa_y}{2\pi}\,\frac{1}{\sqrt{[\epsilon(\vec{\kappa})]^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3}{2U}.}
Having derived the mean field equations, let us now relate this method to the saddle point approximation given above. We consider the final result of the last section,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{a}^{(s)}(\vec{r}, \tau)=Tr\left [\left [\left (\frac{\partial}{\partial \tau} - \mu + \hat{h}_o\right ) + \sqrt{\frac{U}{3}} \phi^{(s)}(\vec{r}', \tau') \cdot \vec{\tau}\right ]_{\alpha \beta}^{-1}\delta(\vec{r}-\vec{r}')\delta(\tau - \tau')\sqrt{\frac{U}{3}}\tau_{\beta\alpha}^a\right ].}
We note that the factor,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left [\left (\frac{\partial}{\partial \tau} - \mu + \hat{h}_o\right ) + \sqrt{\frac{U}{3}} \phi^{(s)}(\vec{r}', \tau') \cdot \vec{\tau}\right ]_{\alpha\beta}^{-1}\delta(\vec{r}-\vec{r}')\delta(\tau-\tau'),}
is just the Green's function for a generalized form of our mean field Hamiltonian (minus the term depending only on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{M}(\vec{r})} ) at equal positions and equal times. Therefore,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{a}^{(s)}(\vec{r}, \tau)=Tr\left [G(\vec{r},\tau;\vec{r},\tau)\sqrt{\frac{U}{3}}\tau^a\right ].}
It is shown, for example, by Fetter and Walecka (A. Fetter and J. D. Walecka, Quantum Theory of Many-Body Systems, McGraw-Hill, New York (1971)), that the above is simply proportional to the average of the spin at a given point:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\phi}^{(s)}(\vec{r},\tau)=\sqrt{\frac{4U}{3}}\langle \vec{S}(\vec{r},\tau)\rangle}
If we take
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\phi}^{(s)}(\vec{r},\tau)=\sqrt{\frac{4U}{3}}\vec{M}(\vec{r})}
and assume that it has the form, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\phi}^{(s)}(\vec{r},\tau)=\vec{\phi}_0\cos(\vec{Q}\cdot\vec{r})} , then we will have reduced the problem to the one that we considered above.
A few comments on mean field theory are in order. First of all, it is only reliable at weak coupling; that is, in our case, when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U\ll t} . This is because the approximation we make involves dropping a term of order Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} ; if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} is too large, then this approximation is questionable. Second of all, this method introduces a bias into our analysis. We assume that the system has a certain order; in this case, we assumed that it was antiferromagnetic. We would require a separate analysis to ensure that the system does, in fact, have the order that we assume. To illustrate these problems, we consider the Hubbard model in one dimension. It has been solved exactly, and it turns out that no ordering tendencies of any kind are present. However, if we perform a mean field analysis much like the one above, we would predict that the system is antiferromagnetic.
With these issues in mind, let us now solve the mean field equation and obtain a value for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|} . We note that the most dominant contributions will come from the region where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})=0} , especially if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|} is small; these regions are those for which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_x+k_y=\pi} . In fact, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|=0,} then there will be a logarithmic singularity along this line. We will take advantage of this fact to find an approximate solution. We may use the trigonometric identity,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos{\kappa_x}+\cos{\kappa_y}=2\cos\left (\frac{\kappa_x+\kappa_y}{2}\right )\cos\left (\frac{\kappa_x-\kappa_y}{2}\right ),}
to rewrite Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})} as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})=-4t\cos\left (\frac{\kappa_x+\kappa_y}{2}\right )\cos\left (\frac{\kappa_x-\kappa_y}{2}\right ).}
We now expand the first factor about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_x+k_y=\pi} and drop the second factor (that is, we assume it is approximately 1; given that the first factor is small, it should not make much difference), obtaining
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})\approx 2t(\kappa_x+\kappa_y-\pi).}
We will also perform the following transformation on the variables of integration:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K=\frac{\kappa_x+\kappa_y-\pi}{2},\,\kappa=\kappa_x-\kappa_y}
This transformation has a Jacobian of 1. We will approximate the new region of integration with a rectangle with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\kappa|<\pi} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |K|<\tfrac{\Lambda}{2}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} is an appropriate cutoff. Since the integrand will be constant with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa} , the integral just gives a constant coefficient. With all of these approximations, the mean field equation becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\Lambda/2}^{\Lambda/2}\frac{dK}{2\pi}\,\frac{1}{\sqrt{16t^2K^2+\tfrac{4}{9}U^2|\vec{M}_0|^2}}=\frac{3}{2U},}
or
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\Lambda/2}^{\Lambda/2}\frac{dK}{2\pi}\,\frac{1}{\sqrt{K^2+\tfrac{1}{36}\left (\tfrac{U}{t}\right )^2|\vec{M}_0|^2}}=\frac{6t}{U}.}
We now use the fact that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int dx\,\frac{1}{\sqrt{x^2+a^2}}=\sinh^{-1}\left (\frac{x}{a}\right )+C}
to obtain
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\pi}\sinh^{-1}\left (\frac{t}{U}\frac{18\Lambda}{|\vec{M}_0|}\right )=\frac{6t}{U}.}
Solving for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|} , we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|=\frac{18t}{U}\frac{\Lambda}{\sinh(6\pi t/U)}.}
If we assume that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U\ll t} , which is necessary for mean field theory to be valid anyway, we may approximate this as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|\approx \frac{36t}{U}\Lambda e^{-6\pi t/U}.}
We see that, as long as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{U}{t}} is small, then so is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{M}_0|} . We also note that we get a non-zero solution for any value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} . In the exact solution, however, we do not get antiferromagnetic order for arbitrary Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} .
1-dimensional lattice excitations
Solitons in polyacetylene
Dimerization in polyacetylene
Polyacetylene is an organic compound that consists of 1D polymer chain of carbon and hydrogen atoms as the lattice points and branches. The structure is basically repetitions of acetylene molecule Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (C_2H_2)} and produces a high electrical conductivity. The interesting part of it is its alternating bonds between single and double ones and will produce a small energy gap within its spectrum band. The energy band makes it behave as a good semi-conductor material which we can practically use as electronic components.
(The structure of Polyacetylene)
Now let's trace how polyacetylene can create such energy gap. First, we assume the chain as 1D lattice chain that contains dimers constructed by alternating bond types. This means that the electron jumps with different probabilities between the sites. The double bond jump is more probable than the single one since it needs lower energy to apply. In addition to that, we also consider the "stifness" and kinetic energy factor. By taking all of these relevant compositions, the Hamiltonian of the chain becomes,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}=\sum_{j}\frac{m}{2}{\dot{u}_{j}}^2+\sum_{j}\frac{\kappa}{2}(u_{j+1}-u_j)^{2}-\sum_{js}(t_{j+1,j}{c_{j+1,s}}^{\dagger}c_{j,s}+h.c)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{n+1,n} = t_o - \alpha\left(u_{n+1}-u_n\right)}
Some simplifications can be made by getting rid of the kinetic term cause the mass is relatively too big for the detail energy dynamics. Then we can assume 2 interdependent fixed energies of hopping term, means the single bond expands with a certain number from equilibrium while the double bond contracts with the same number
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{j} = \pm (-1)^n u_o}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} t_{j+1,j} &\Rightarrow t_o - t_1 ...... single\\ &\Rightarrow t_o + t_1 ...... double \end{align} }
This difference creates dimers model and so we can separate the lattice into 2 which are the odd and even parts with half filling for each. Then we can rewrite the Hamiltonian as,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}=\sum_{j}\frac{\kappa}{2}(u_{j+1}-u_j)^{2}-(t_o-t_1)\sum^{N/2}_{js}({c_{2j-1,s}}^{\dagger}c_{2j,s}+h.c)-(t_o+t_1)\sum^{N/2}_{js}({c_{2j+1,s}}^{\dagger}c_{2j,s}+h.c)}
Now, we want to couple all separate sites as few modes. That's why we have to Fourier transform the creation and annihilation operators form lattice space to momentum space.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{2j-1,s} = \sqrt{\frac{2}{N}}\sum^{N/2}_{k=1}e^{i\frac{2\pi}{N}k(2j-1)}a_s (k)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_{2j,s} = \sqrt{\frac{2}{N}}\sum^{N/2}_{k=1}e^{i\frac{2\pi}{N}k(2j)}b_s (k)}
These new operators already commute to each other. Let's replace both inside the Hamiltonian as,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathcal{H}_{hop}&=-(t_o-t_1)\sum^{N/2}_{s,k=1}(e^{i\frac{2\pi}{N}k}{a_s (k)}^{\dagger}b_s (k) +h.c)-(t_o+t_1)\sum^{N/2}_{s,k=1}(e^{-i\frac{2\pi}{N}k}{a_s (k)}^{\dagger}b_s (k) +h.c)\\ &=-\sum^{N/2}_{s,k=1}[2t_o cos(\frac{2\pi}{N}k)-2t_1 i sin(\frac{2\pi}{N}k)]{a_s (k)}^{\dagger}b_s (k)-\sum^{N/2}_{s,k=1}[2t_o cos(\frac{2\pi}{N}k)+2t_1 i sin(\frac{2\pi}{N}k)]{b_s (k)}^{\dagger}a_s (k)\\ \end{align} }
By doing matrix rearrangement and diagonalize it, we get 2 modes of single particle excitation spectrum which is,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(k)=\pm 2t_o \sqrt{{cos}^2 \left(\frac{2\pi}{N}k\right)+\left(\frac{t_1}{t_o}\right)^2 {sin}^2 \left(\frac{2\pi}{N}k\right)}}
If we plot this spectrum we'll get the maximum width between 2 modes and their gap which are equal to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4t_o \approx 10 eV}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4t_1 \approx 1.4 eV}
.
Finally we need to discuss some structure possibilities of polyacetylene. It can have cis or trans molecule which are mirrored with each other or could even be a mix of them. If it is so, then there will be a boundary in between which we call it domain wall, behaving like a localized, stable, and dynamic soliton. A neutral soliton is proposed to be one bond length unpaired spin wall that makes it harder to move to other sites. Nowadays, the focus of polyacetylene research is the wide-range control possibility of the doped one. This doping might come from charged domain walls since it shows some interesting properties like anomalous magnetic susceptibility, infrared absorbtion, and power from temperature.
Soliton formation in polyacetylene
One studied excitation of polyacetylene is the formation of solitons. In this context, a soliton manifests as the boundary between two domains of the polyacetylene mono-chain. To illustrate this, consider that the ground state of our dimerized chain is two-fold degenerate with respect to the ordering of double and single bonds. That is, the chain can have an abab formation or a baba formation:
abab formation
baba formation
The mono-chain can comprise adjacent domains of state A and B, and there is inevitably a kink in the chain where the domains meet. At this point, instead of strictly alternating bonds (ababa), there must be two or more of the same bond in a row (babbab):
abaaba
The dashed line, or domain wall, is referred to as a soliton. It can have any length greater than or equal to one bond length, where the soliton pictured above has length 1 by convention. Additionally, it can move along the polyacetylene chain. The formation of a soliton is associated with an activation energy that depends on the size and velocity of the soliton, as well as on the existing band structure of the chain.
Recall that when we modeled polyacetylene as a dimerized lattice with half filling of electrons and next-neighbor hoppings, we discovered a double band structure given by the dispersion relation
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(k)=\pm 2t_o \sqrt{{cos}^2 \left(\frac{2\pi}{N}k\right)+\left(\frac{t_1}{t_o}\right)^2 {sin}^2 \left(\frac{2\pi}{N}k\right)}} .
These bands are pictured in the figure below, where the positive energy band has been folded out into the second Brillouin zone.
We find that even for an infinitesimal Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha}
we observe dimerization, and thus a finite energy gap between bands. Our hamiltonian allows for direct control of the size of this gap through the free parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha}
, and to calculate the activation energy of solitons for various gap sizes and soliton lengths. In the figure below, the system energy is plotted vs the soliton length for three gap sizes:
It is found that the natural soliton length decreases as a function of increasing band gap. This is interesting because as the material becomes an insulator, the solitons become shorter and have a higher energy.
This section is largely a review of W.P. Su, J.R. Shrieffer, and A.J. Heeger's Solitons in Polyacetylene, PRL V42 n25.
Properties of solitons
Until 1979 charge and spin quantum numbers were related to integer number of electron and holes in a system. But the discovery of Solitons in Polyacetylene by Su , Schreiffer and Heeger ( Phys. Rev. Lett. 42, 1698 (1979)) lead to a new concept of fractional quantum numbers. These numbers are observed experimentally in material physics.
Solitons carry parts of elementary quantum number i.e. it can either have charge e and spin 0 or charge 0 and spin ½. Consider the A and B phase of Polyacetylene.If we remove one of the bonds, a domain wall is introduced in the chain which separates the two phases A and B. This describes a soliton with a length of only one bond, making it the most elementary defect.
At every local site of the chain there are 2 core electrons, 3 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} electrons and 1 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} electron attributed to Carbon atoms and 1 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} electron from Hydrogen atom. Hence every bond has a charge 2e and spin 0, all electrons are paired. Since each domain wall is half a bond they carry a charge e and spin 0. This break up of quantum numbers in Solitons is homotopically distinct from free electrons which always has a charge e and spin ½. If any of the left over orbital at the local site were singly occupied then the Solitons will have charge 0 and spin ½. These numbers have been verified by experimental techniques like Electron Paramagnetic Resonance. For larger l ( domain wall width) fractions of electric charge are unavoidable.
Solitons have an effective mass of about six times the mass of an electron. This effective mass is related to the fact that the domain walls are mobile and have an associated inertia.
Doping of Polyacetylene is of particular interest because the energy required to create a Soliton is lesser than band excitations which makes them a excellent charge carriers in insulators.
Coulomb interacting electron Gas
Jellium model
In this chapter we are going to study the Coulomb interacting electron gas by using the Jellium model. The Jellium model is a very simple model for interacting electrons hosted in a three dimensional solid. Electronic interactions are taken to be of the Coulomb type. The ions making up the solid are treated in the simplest possible way, namely as an inert positive uniform background of charges that insures overall charge neutrality Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{V} d^3 r \rho \left(r\right)=0 } . Despite its simplicity, the Jellium model is very instructive as it displays interesting many-body effects. Using the Jellium model we can calculate the binding energy of the system in very good approximation. However, we cannot use this model to obtain either the attraction of electrons that lead to superconductivity or the phonon distribution to the specific heat since from this picture we do not get any phonons.
The Hamiltonian for the Jellium model is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}H&=-\frac{\hbar}{2m} \sum_{\sigma=\uparrow\downarrow}\int d^3 r \Psi^{\dagger}_{\sigma} ( r )\nabla^2 \Psi_{\sigma}( r)-\sum_{\sigma={\uparrow\downarrow}}\int d^3 r\int d^3 r' \Psi_{\sigma}^{\dagger}( r)\Psi_{\sigma}( r)\frac{e^2}{|r-r'|} \exp^{-\frac{|r-r'|}{\xi}}n_{b}( r') \\ &+\frac{1}{2}\sum_{\sigma\sigma'}\int d^3r\int d^3r' \frac{e^2}{|r-r'|}\exp^{-\frac{|r-r'|}{\xi}}\Psi_{\sigma}^{\dagger}( r)\Psi_{\sigma'}^{\dagger}( r')\Psi_{\sigma'}( r')\Psi_{\sigma}( r) \\&+\frac{1}{2}\int d^3 r\int d^3 r' n_{b}( r)\frac{e^2}{|r-r'|}\exp^{-\frac{|r-r'|}{\xi}} n_{b}( r')\end{align}}
,where the first term is the kinetic energy, the second is the electron-ions interaction, the third is the electron-electron interaction and the fourth is the repulsion between the background ions. Moreover, the factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \exp^{-\frac{|r-r'|}{\xi}}} is being used to perform the calculations easier. We will set the range Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi\rightarrow\infty} at the end of the calculations to get back the infinite Coulomb range interaction.
For uniform background density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{b}=\frac{N}{V}} the last term will give:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{1}{2}\left(\frac{N}{V}\right)^2 e^2\int d^3 r\int d^3 r' \frac{1}{|r-r'|}\exp^{-\frac{|r-r'|}{\xi}}&=\\ \frac{1}{2}\left(\frac{N}{V}\right)^2 e^2 V \int d^3\tau\frac{1}{|\tau|}\exp^{-\frac{\tau}{\xi}}&=\frac{e^2}{2}\frac{N^2}{V}4\pi \xi^2 \end{align}}
the second term will give:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -e^2\frac{N}{V}\sum_{\sigma}\int d^3 r\Psi_{\sigma}^{\dagger}( r)\Psi_{\sigma}( r)\int d^3 r'\frac{1}{|r-r'|}\exp^{-\frac{|r-r'|}{\xi}}= -e^2\frac{N}{V}\hat{N_{e}}4\pi\xi^2 }
where we have used that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\sigma}\int d^3 r\Psi_{\sigma}^{\dagger}( r)\Psi_{\sigma}( r)=\hat{N_{e}}}
the number operator of electrons
The third term (e-e interaction) is more complicated. We will go to the momentum representation via the Fourier transform of the fields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi_{\sigma}( r)=\frac{1}{\sqrt{V}}\sum_{k}\exp^{irk}\Psi_{k\sigma}} , with the anti commutation relations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\Psi_{k\sigma},\Psi_{k'\sigma'}^{\dagger}\}=\delta_{kk'}\delta_{\sigma\sigma'}} .
Using that formulation our expression becomes
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{1}{2}&\sum_{\sigma\sigma'}\int d^3 r\int d^3 r'\frac{e^2}{|r-r'|}\exp^{-\frac{|r-r'|}{\xi}}\frac{1}{V^2}\sum_{k_1,k_2,k_3,k_4}\exp^{-ik_{1}r}\exp^{-ik_{2}r}\exp^{ik_{3}r}\exp^{ik_{4}r}\Psi_{k_1,\sigma}^{\dagger}\Psi_{k_2,\sigma'}^{\dagger}\Psi_{k_3,\sigma'}\Psi_{k_4,\sigma}\\ &=\frac{1}{2}\sum_{\sigma,\sigma'}\frac{1}{V^2}\sum_{k_1,k_2,k_3,k_4}\Psi_{k_1,\sigma}^{\dagger}\Psi_{k_2,\sigma'}^{\dagger}\Psi_{k_3,\sigma'}\Psi_{k_4,\sigma}\int d^3 \mu\frac{e^2}{|\mu|}\exp^-\frac{|\mu|}{\xi} \times \int d^3 R \exp^{-i(k_{1}-k_{4})(R+\frac{1}{2}\mu)}\exp^{-i(k_{2}-k_{3})(R-\frac{1}{2}\mu)}\\ &=\frac{1}{2}\sum_{\sigma,\sigma'}\frac{1}{V}\sum_{k_1,k_2,k_3,k_4}\delta_{k_{1}-k_{4},k_{3}-k_{2}}\Psi_{k_1,\sigma}^{\dagger}\Psi_{k_2,\sigma'}^{\dagger}\Psi_{k_3,\sigma'}\Psi_{k_4,\sigma}\int d^3 \mu \frac{e^2}{|\mu|}\exp^{-\frac{|\mu|}{\xi}}\exp^{-i(k_{1}-k_{4}+k_{2}-k_{3})\frac{1}{2}\mu} \end{align}}
We change variables, going to the rest frame of the centre of mass, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R=\frac{r+r'}{2}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu=r-r'} . Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_1=k, k_4=k-q} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_2=k', k_3=k'+q} . The equation becomes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}\sum_{\sigma,\sigma'}\frac{1}{V}\sum_{k,k'}\sum_{q}\Psi_{k,\sigma}^{\dagger}\Psi_{k',\sigma'}^{\dagger}\Psi_{k'+q,\sigma'}\Psi_{k-q,\sigma}\int d^3 \mu \frac{e^2}{|\mu|}\exp^{-\frac{|\mu|}{\xi}}\exp^{-i\bold{q}\cdot \bold{\mu}} =\frac{1}{2}\sum_{\sigma,\sigma'}\frac{1}{V}\sum_{k,k'}\sum_{q}\Psi_{k,\sigma}^{\dagger}\Psi_{k',\sigma'}^{\dagger}\Psi_{k'+q,\sigma'}\Psi_{k-q,\sigma}\frac{4\pi e^2}{q^2+\xi^2} }
Now if we separate the case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q=0} we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{1}{2}\sum_{\sigma,\sigma'}\frac{1}{V}\sum_{k,k'}\Psi_{k,\sigma}^{\dagger}\Psi_{k',\sigma'}^{\dagger}\Psi_{k'+q,\sigma'}\Psi_{k-q,\sigma}4\pi\xi^2 e^2 +\frac{1}{2}\sum_{\sigma,\sigma'}\frac{1}{V}\sum_{k,k'}\sum_{q\not=0}\Psi_{k,\sigma}^{\dagger}\Psi_{k',\sigma'}^{\dagger}\Psi_{k'+q,\sigma'}\Psi_{k-q,\sigma}\frac{4\pi e^2}{q^2+\xi^2}\\ = \frac{1}{2V}e^2 4\pi\xi^2(\hat{N_{e}^2}-\hat{N_{e}})+\frac{1}{2}\sum_{\sigma,\sigma'}\frac{1}{V}\sum_{k,k'}\sum_{q\not=0}\Psi_{k,\sigma}^{\dagger}\Psi_{k',\sigma'}^{\dagger}\Psi_{k'+q,\sigma'}\Psi_{k-q,\sigma}\frac{4\pi e^2}{q^2+\xi^2} \end{align}}
Combining these results under the charge neutrality condition Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{N_{e}}=N} and setting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi\rightarrow\infty} we get the Hamiltonian for the Coulomb gas
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{k,\sigma}\frac{\hbar^2k^2}{2m}\Psi_{k\sigma}^{\dagger}\Psi_{k\sigma}+\frac{1}{2V}\sum_{\sigma,\sigma'}\sum_{k,k'}\sum_{q\not=0}\frac{4\pi e^2}{q^2}\Psi_{k,\sigma}^{\dagger}\Psi_{k',\sigma'}^{\dagger}\Psi_{k'+q,\sigma'}\Psi_{k-q,\sigma} }
In order to calculate the binding energy of the system we need the partition function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=Tr[\exp^{-\beta(\hat{H}-\mu\hat{N})}]=Z_{0}\langle\exp^{-{S_{int}}}\rangle=\exp^{-\beta\Omega}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{int}=\int_{0}^{\beta}d\tau\frac{1}{2V}\sum_{\sigma,\sigma'}\sum_{k,k'}\sum_{q\not=0}\frac{4\pi e^2}{q^2}\Psi_{k,\sigma}^{\dagger}(\tau)\Psi_{k',\sigma'}^{\dagger}(\tau)\Psi_{k'+q,\sigma'}(\tau)\Psi_{k-q,\sigma}(\tau) }
We are going to use the cumulant expansion Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\exp^{-S_{int}}\rangle=\exp^{-\langle S_{int}\rangle}\exp^{\frac{1}{2}(\langle S_{int}^2\rangle-\langle S_{int}\rangle^2)}} to calculate the binding energy up to second order in perturbation theory. In addition, we are going to use Wick's theorem to reduce arbitrary products of creation and annihilation operators to sums of products of pairs of these operators. Meaning that we have to sum all the possible contractions for the field operators.
For the 1st order we have two possible contractions. The first gives rise to the Hartree term and the second to the Fock term.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle S_{int} \rangle =\int_{0}^{\beta}\frac{1}{2V}\sum_{k,k'}\sum_{\sigma,\sigma'}\sum_{q\not=0}\frac{4\pi e^2}{q^2} \langle \Psi_{k,\sigma}^{\dagger}(\tau)\Psi_{k',\sigma'}^{\dagger}(\tau)\Psi_{k'+q,\sigma'}(\tau)\Psi_{k-q,\sigma}(\tau)\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\int_{0}^{\beta}\frac{1}{2V}\sum_{k,k'}\sum_{\sigma,\sigma'}\sum_{q\not=0}\frac{4\pi e^2}{q^2}\{G_{0}(k-q,\tau;k,\tau)G_{0}(k'+q,\tau;k',\tau)-G_{0}(k'+q,\tau;k,\tau)G_{0}(k-q,\tau;k',\tau)\}}
The corresponding Feynman diagrams are
Where the one particle Green's function is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_0(\lambda,\tau;\lambda',\tau')=\delta_{\lambda,\lambda'}\exp^{-(E_{\lambda}-\mu)(\tau-\tau')}\left[\Theta(\tau-\tau')(1+\xi n(E_{\lambda}))+\Theta(\tau'-\tau)\xi n(E_{\lambda})\right] } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{0}\left(\lambda,\tau;\lambda',\tau\right)=\xi\delta_{\lambda,\lambda'}n(E_{\lambda}) }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi=+1} for bosons and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi=-1} for fermions. The Green's functions of the Hartree term force Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k-q=q} which means that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q=0} . But, we have excluded the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q=0} case, so this term vanishes.So we are left only with the Fock term which yields
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle S_{int}\rangle=-\sum_{\sigma}\int_{0}^{\beta}d\tau\frac{1}{2V}\sum_{k}\sum_{q\not=0}\frac{4\pi e^2}{q^2}n_{F}(E_{k})n_{F}(E_{k-q})=-\sum_{\sigma}\frac{\beta}{2V}\sum_{k}\sum_{q\not=0}\frac{4\pi e^2}{q^2}n_{F}(E_{k})n_{F}(E_{k-q})=\beta\Omega^{(1)}}
Through the partition function we can find the grand canonical potential (or Landau potential) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=\exp^{-\beta\Omega}} .
The noninteracting term takes the form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{0}=\prod_{k,\sigma}(1+\exp^{-\beta(E_{k}-\mu)})=\exp^{\frac{\beta}{\beta}2V\int\frac{d^3k}{(2\pi)^3}\ln(1+\exp^{-\beta(E_{k}-\mu)})}=\exp^{-\beta\Omega^{(0)}}}
For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\rightarrow 0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu=\frac{\hbar^2k_{F}^2}{2m}} we have:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega^{(0)}=\int\frac{d^3k}{(2\pi)^3}\Theta(\mu-E_{k}) \times(E_{k}-\mu)=\frac{2}{(2\pi)^3}\int_{0}^{k_{F}}k^2 dk 4\pi(\frac{\hbar^2k^2}{2m}-\mu)=-\frac{1}{2\pi^2}\frac{\hbar^2k_{F}^2}{2m}\frac{2}{15} }
The first order interaction term for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\rightarrow 0} gives
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega^{(1)}=-\frac{e^2}{2V}\sum_{\sigma}\sum_{k}\sum_{q\not=0}\frac{4\pi}{q^2}n_{F}(E_{k})n_{F}(E_{k-q}) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{e^2}{2V}\sum_{\sigma}\sum_{k}\sum_{q\not=0}\frac{4\pi}{q^2}\Theta(k_{F}-|k|)\Theta(k_{F}-|k-q|) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-4\pi e^2\sum_{k}\int \frac{d^3k'}{(2\pi)^3}\frac{1}{(k-k')^2}\Theta(k_{F}-|k|)\Theta(k_{F}-|k'|)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{32\pi^3 e^2}{(2\pi)^2}\int_{0}^{k_{F}}k^2dk\int_{0}^{k_{F}}k'^2dk'\int_{0}^{\pi}\sin\theta_{k'}d\theta_{k'}\frac{1}{k^2+k'^2-kk'\cos\theta_{k'}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{e^2k_{F}^4}{2\pi^3}I=-\frac{e^2k_{F}^4}{4\pi^3}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I=\int_{0}^{1}x^2dx\int_{0}^{1}y^2dy\int_{-1}^{1}\frac{du}{x^2+y^2-2xyu}=\frac{1}{2}}
Now we are going to use the two results we obtained to calculate the Helmholtz free energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{F}{V}=\frac{\Omega}{V}+\mu\frac{N}{V}} . From these equations we get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{V}(\Omega^{(0)}+\Omega^{(1)})=-\frac{2}{15}\frac{k_{F}^3}{\pi^2}\frac{\hbar^2k_{F}^2}{2m}-\frac{e^2}{4\pi^3}k_{F}^4 }
Also Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=-\frac{\partial\Omega}{\partial\mu}=\frac{\partial\Omega}{\partial k_{F}}\frac{\partial k_{F}}{\partial\mu}=\frac{k_{F}^3}{3\pi^2}+\frac{me^2k_{F}^2}{\hbar^2\pi^3} }
by expanding for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{F}=k_{F}^{(0)}+\delta k_{F}} we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{N}{V}=\frac{(k_{F}^{(0)})^3}{3\pi^2}+\frac{(k_{F}^{(0)})^2\delta k_{F}}{\pi^2}+\frac{m e^2}{\hbar^2\pi^3}(k_{F}^{(0)})^2+O(\delta k_{F}^2) }
where since we have fixed number of particles in our system we can find the correction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta k_{F}} by setting the second and third term equal to zero, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta k_{F}} So for the Helmholtz free energy using the same expansion we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{F}{V}&=-\frac{2}{15}\frac{k_{F}^3}{\pi^2}\frac{\hbar^2k_{F}^2}{2m}-\frac{e^2}{4\pi^3}k_{F}^4+\frac{\hbar^2 k_{F}^{2}}{2m}\frac{(k_{F}^{(0)})^3}{3\pi^2}=-\frac{2}{15\pi^2}\frac{\hbar^2}{2m}\left[(k_{F}^{(0)})^5+5k_{F}^{(0)}\delta k_{F}+O(\delta _{F}^2)\right]-\frac{e^2(k_{F}^{(0)})^4}{4\pi^3}\\&+\frac{\hbar^2}{2m}\left[(k_{F}^{(0)})^2+2k_{F}^{(0)}\delta k_{F}+O(\delta k_{F}^2)\right]\frac{(k_{F}^{(0)})^3}{3\pi^2}=\frac{\hbar^2(k_{F}^{(0)})^5}{2m}\frac{1}{5\pi^2}-\frac{e^2(k_{F}^{(0)})^4}{4\pi^3} \end{align}}
which can be written by setting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{B}=\frac{\hbar^2}{me^2}} (Bohr radius), Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{N}{V}=\frac{4\pi}{3}r_{0}^3} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{s}=\frac{r_{0}}{a_{B}}} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{F}{V}=\frac{\hbar^2}{2m}(k_{F}^{(0)})^5\frac{1}{5\pi^2}\left[1-\frac{1}{\pi}\frac{5}{2}\frac{1}{a_{B}k_{F}^{(0)}}+\cdots\right]=\frac{e^2}{2a_{B}}\left(\frac{2.21}{r_{s}^2}-\frac{0.91}{r_{s}}+\cdots\right) }
In order to go beyond these corrections we have to calculate the second order term in the perturbation theory, which give the so called correlation energy.The second order in the Cumulant expansion is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}(\langle S_{int}^2\rangle-\langle S_{int}\rangle^2)=\frac{1}{2}\int_{0}^{\beta}d\tau\int_{0}^{\beta}d\tau'\left(\frac{e^2}{2V}\right)^2\sum_{k,k'}\sum_{\sigma,\sigma'}\sum_{q\not=0}\sum_{p,p'}\sum_{s,s'}\sum_{q' \not=0} \langle\Psi_{k,\sigma}^{\dagger}(\tau)\Psi_{k',\sigma'}^{\dagger}(\tau)\Psi_{k'+q,\sigma'}(\tau)\Psi_{k-q,\sigma}(\tau) \Psi_{p,s}^{\dagger}(\tau')\Psi_{p',s'}^{\dagger}(\tau')\Psi_{p'+q',s'}(\tau')\Psi_{p-q',s}(\tau')\rangle }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +\frac{1}{2}\int_{0}^{\beta}d\tau\int_{0}^{\beta}d\tau'\left(\frac{e^2}{2V}\right)^2\sum_{k,k'}\sum_{\sigma,\sigma'}\sum_{q\not=0}\sum_{p,p'}\sum_{s,s'}\sum_{q' \not=0} \langle\Psi_{k,\sigma}^{\dagger}(\tau)\Psi_{k',\sigma'}^{\dagger}(\tau)\Psi_{k'+q,\sigma'}(\tau)\Psi_{k-q,\sigma}(\tau)\rangle\langle \Psi_{p,s}^{\dagger}(\tau')\Psi_{p',s'}^{\dagger}(\tau')\Psi_{p'+q',s'}(\tau')\Psi_{p-q',s}(\tau')\rangle }
The second term in this equation gives the disconnected diagrams which are going to cancel out. Moreover, any contraction of the type Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi_{p',s'}^{\star}(\tau')\Psi_{p'+q',s'}(\tau')}
(tadpole diagrams) is going to vanish because the charge neutrality forces Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\not=0}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q'\not=0}
. Due to this simplification from the total 24 ways of contacting the field operators we are left with 8.
Let us list all the possible contractions which will give the following Green's functions terms
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_{\sigma,\sigma'}G_{0}(k'+q,\tau;k,\tau)\delta_{\sigma',s'}G_{0}(p'+q',\tau';k',\tau)\delta_{\sigma,s}G_{0}(k-q,\tau;p,\tau')(-1)\delta_{s,s'}G_{0}(p-q',\tau';p',\tau')+\delta_{\sigma,\sigma'}G_{0}(k'+q,\tau;k,\tau)(-1)\delta_{s,\sigma'}G_{0}(p-q',\tau';k',\tau) (-1)\delta_{\sigma,s'}G_{0}(k-q,\tau;p',\tau')(-1)\delta_{s,s'}G_{0}(p'+q',\tau';p,\tau') }
These two terms are the same under the shift Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p\rightarrow p'} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q'\rightarrow -q'} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s\rightarrow s'}
Next we get the terms
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \delta_{\sigma,\sigma'}G_{0}(p'+q',\tau';k,\tau)\delta_{\sigma,s}G_{0}(k-q,\tau;p,\tau')\delta_{\sigma',s'}G_{0}(k'+q,\tau;p',\tau')(-1)\delta_{\sigma',s}G_{0}(p-q',\tau';k',\tau)\\+\delta_{\sigma,s'}G_{0}(p'+q',\tau';k,\tau)(-1)\delta_{\sigma,s'}G_{0}(k-q,\tau;p',\tau')\delta_{\sigma',s}G_{0}(k'+q,\tau;p,\tau')(-1)\delta_{\sigma',s}G_{0}(p-q',\tau';k',\tau)&\\+\delta_{\sigma,\sigma'}G_{0}(p'+q',\tau';k,\tau)\delta_{\sigma,\sigma'}G_{0}(k-q,\tau;k',\tau)\delta_{\sigma',s}G_{0}(k'+q,\tau;p,\tau')(-1)\delta_{s,s'}G_{0}(p-q',\tau';p',\tau') \end{align}}
Finally we also have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \delta_{\sigma,s}G_{0}(k-q,\tau;p,\tau')\delta_{\sigma',s'}G_{0}(k'+q,\tau;p',\tau')\delta_{\sigma',s'}G_{0}(p'+q',\tau';k',\tau)\delta_{\sigma,s}G_{0}(p-q',\tau';k,\tau)\\-\delta_{\sigma,s'}G_{0}(k-q,\tau;p',\tau')\delta_{\sigma',s}G_{0}(k'+q,\tau;p,\tau')\delta_{\sigma',s'}G_{0}(p'+q',\tau';k',\tau)\delta_{\sigma,s}G_{0}(p-q',\tau;k,\tau)\\-\delta_{\sigma,s}G_{0}(p-q',\tau';k,\tau)\delta_{\sigma,s'}G_{0}(k-q,\tau;k',\tau)\delta_{\sigma',s'}G_{0}(k'+q,\tau;p',\tau')\delta_{s,s'}G_{0}(p'+q',\tau';p,\tau') \end{align}}
We can observe that under proper shifts some equations give the same result.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\rightarrow k'} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma\rightarrow \sigma'} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\rightarrow -q}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p\rightarrow p'} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\rightarrow k'} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\rightarrow -q'} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\rightarrow -q}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\rightarrow k'} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\rightarrow-q}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p\rightarrow p'} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q'\rightarrow-q'} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s\rightarrow s'}
The corresponding Feynman diagrams are
As a result we have to calculate only three terms. We have 4 times the first which is giving
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{\beta\Omega^{(2)}}{V}&=-\frac{1}{2}\int_{0}^{\beta}d\tau\int_{0}^{\beta}d\tau'\left(\frac{e^2}{2V}\right)^2\sum_{k,k'}\sum_{\sigma,\sigma'}\sum_{q,q'\not=0}\sum_{p,p'}\sum_{s,s'}\frac{4\pi}{q^2}\frac{4\pi}{q'^2}4\delta_{\sigma,\sigma'}G_{0}(k'+q,\tau;k,\tau)\delta_{\sigma',s'}G_{0}(p'+q',\tau';k',\tau)\delta_{\sigma,s}\\&G_{0}(k-q,\tau;p,\tau')(-1)\delta_{s,s'}G_{0}(p-q',\tau';p',\tau')\\&=(4\pi e^2)^2\int_{0}^{\beta}d\tau\int_{0}^{\beta}d\tau'\sum_{k}\int\frac{d^3q}{(2\pi)^3}\int\frac{d^3q'}{(2\pi)^3}\frac{1}{q^2}\frac{1}{q'^2}\exp^{-(E_{k-q}-\mu)(\tau-\tau')}\\& \left(\Theta(\tau-\tau')-n_{F}(E_{k-q})\right)(-n_{F}(E_{k}))\exp^{-(E_{k-q}-\mu)(\tau-\tau')}\left(\Theta(\tau-\tau')-n_{F}(E_{k-q})(-n_{F}(E_{k-q-q'}))\right)\\&=(4\pi e^2)^2\beta\sum_{k}\int\frac{d^3q}{(2\pi)^3}\int\frac{d^3q'}{(2\pi)^3}\frac{1}{q^2}\frac{1}{q'^2}n_{F}(E_{k-q})(n_{F}(E_{k-q})-1)n_{F}(E_{k})n_{F}(E_{k-q-q'}) \end{align}}
this calculation is giving a finite result. From the second we are going to end up with a finite result
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\Omega^{2}}{V}=(4\pi e^2)^2\int\frac{d^3k}{(2\pi)^3}\int\frac{d^3q}{(2\pi)^3}\int\frac{d^3p}{(2\pi)^3}\frac{1}{q^2}\frac{1}{(p-(k+q))^2}\frac{1}{E_{k+q}+E_{p-q}-E_{k}-E_{k+q+q'}} n_{F}(E_{k})n_{F}(E_{p})(1-n_{F}(E_{k+q}))(1-n_{F}(E_{p-q})) }
and from the last term (ring diagrams)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\Omega^{2}}{V}=-2(4\pi e^2)^2\int\frac{d^3k}{(2\pi)^3}\int\frac{d^3k'}{(2\pi)^3}\int\frac{d^3q}{(2\pi)^3}\frac{1}{q^4}\frac{1}{E_{k}-E_{k-q}-E_{k'}+E_{k'-q}} (1-n_{F}(E_{k})n_{F}(E_{k})n_{F}(E_{k'})(1-n_{F}(E_{k'-q})) }
which is giving a divergent result which can be seen if we perform the integrations over k and k' (for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\rightarrow 0} ). We will see that we get a linear dependence on q and since we have an overall Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{q^3}} dependence the integration over q will diverge. Let's perform the integrations over k and k' to realise that behavior.
So for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\rightarrow 0} the occupation factors will transform in Theta functions which are going to change the limits of the integration. By using two intersecting spheres in k space we can easily figure out what the integration limits will be. The result is an integral of the following form
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{2\pi}d\phi\int_{0}^{2\pi}d\phi'\int_{\frac{q}{2\sqrt{2m\mu}}}^{1}d(\cos(\theta))\int_{\sqrt{2m\mu}}^{\sqrt{2m\mu-q^2\sin^2{\theta}}+q\cos{\theta}}dk k^2\int_{-1}^{\frac{q}{2\sqrt{2m\mu}}}d\cos{\theta'}\int_{\sqrt{2m\mu-q^2\sin^2{\theta'}}+q\cos{\theta'}}^{\sqrt{2m\mu}}dk' k'^2\frac{m}{kq\cos{\theta}-k'q\cos{\theta'}} }
where for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\rightarrow 0} we can assume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=k'} and the integration in first order in q will give the linear dependence as we mentioned.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{\frac{q}{2\sqrt{2m\mu}}}^{1}dx\int_{-1}^{\frac{q}{2\sqrt{2m\mu}}}dy\frac{(2m\mu)^2 m}{\sqrt{2m\mu}}\frac{-q^2}{q}\frac{xy}{x-y}\overset{q\rightarrow 0}{\longrightarrow}(2m\mu)^{\frac{3}{2}}mq\frac{2}{3}(1-\ln{2})+O(q^3) }
The problem of this divergence is resolved by resuming the series of the ring diagrams. This procedure is called the RPA approximation and it is going to be the subject of the following section.
Ring Divergence Removal with RPA
Since the ring diagrams are divergent, and of increasing divergence as the perturbation theory order increases, we are going to ignore the other terms in the action and focus on them. The ring diagrams appear from the second order and up so it is reasonable to single them out. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle\sum_{n=1}^{\infty}\frac{(-1)^n}{n!}\langle S_{int}^{n}\rangle=- \langle S_{int}\rangle_{0,c}+\displaystyle\sum_{n=2}^\infty\frac{(-1)^n}{n!}\langle S_{int}^{ n}\rangle_{0,c}^{ring}} At first order we have:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle S_{int}^{n}\rangle=\int_0^\beta d\tau \frac{1}{2V} \displaystyle\sum_{q \neq 0}\frac{4\pi e^2}{q^2} ( \displaystyle\sum_{k,\sigma} \psi^*_{k\sigma}\psi_{k-q,\sigma})(\displaystyle\sum_{k',\sigma'} \psi^*_{k'\sigma'}\psi_{k'+q,\sigma'})}
Defining the the operator:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_q(\tau)=\displaystyle\sum_{k,\sigma} \psi^*_{k\sigma}(\tau)\psi_{k+q,\sigma}(\tau) ; n_q^*(\tau)=\displaystyle\sum_{k,\sigma} \psi^*_{k\sigma}(\tau)\psi_{k-q,\sigma} (\tau)}
The n-th order of the action will have n imaginary time integrals and the contraction of all the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_q} operators at diffrent times. Calling the fourier component of the interaction potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_q} , the n-th order term looks like:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle S_{int}^{n}\rangle=\int_0^\beta d\tau_1 ... d\tau_n \displaystyle\sum_{q_1..q_n \neq 0}V_{q_1}...V_{q_n} \langle n^*_{q_1}(\tau_1)n_{q_1}(\tau_1)n^*_{q_2}(\tau_2)n_{q_2}(\tau_2)...n^*_{q_n}(\tau_n)n_{q_n}(\tau_n)\rangle}
Since we are only considering connected diagrams, the contractions will force all the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_{i} } to become the same q as each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{q_i}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^*_{q_j}} are connected to diffrent Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^*_{q_k}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{q_l}} respectively.
Therefore, all the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{q_i}} terms will collapse to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (V_q)^n} . The amount of contractions that we can make is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{n-1}(n-1)!} . Defining the contraction between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^*_q(\tau_i)} with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_q(\tau_j)} as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n^*_q(\tau_i) n_q(\tau_j) \rangle_{0,c} = \Pi_q(\tau_i-\tau_j) }
Which is called the Corellator. The expression now becomes:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle S_{int}^{n}\rangle=\frac{(n-1)!}{2} \int_0^\beta d\tau_1 ... d\tau_n (V_q)^n \Pi_q(\tau_1-\tau_2)\Pi_q(\tau_2-\tau_3)...\Pi_q(\tau_n-\tau_1) }
In order to decouple the correlators we transform to Matsubara frequency space by utilizing: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_q(\tau)=\frac{1}{\beta} \displaystyle\sum_{n=-\infty}^{+ \infty} e^{i \Omega_n \tau} \Pi_{q,\Omega_n}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_{q,\Omega_n}=\int d\tau e^{-i \Omega_n \tau} \Pi_q(\tau) } Transforming, we get:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle S_{int}^{n}\rangle =\frac{1}{\beta^n} \displaystyle\sum_{m_1..m_2} \int_0^\beta d\tau_1 ... d\tau_n \displaystyle\sum_{q \neq 0} V^n_q e^{i \Omega_{m_1} (\tau_1-\tau_2) } \Pi_{q,\Omega_{m_1}}...e^{i \Omega_{m_n} (\tau_n-\tau_1) } \Pi_{q,\Omega_{m_n}}}
The orthogonality of the exponentials will force all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_{m_i}} 's to collapse to the same Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega_m} when we integrate over the imaginary time variables. So we have:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle S_{int}^{n}\rangle=\frac{(n-1)!}{2} \displaystyle\sum_{q\neq 0} \displaystyle\sum_m (V_q \Pi_{q,\Omega_m})^n}
Putting this back to (1):
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle\sum_{n=1}^{\infty}\frac{(-1)^n}{n!}\langle S_{int}^{ n}\rangle=- \langle S_{int}\rangle_{0,c} +\frac{1}{2}\displaystyle\sum_{n=2}^\infty\frac{(-1)^n}{n} \displaystyle\sum_{q\neq 0} \displaystyle\sum_m (V_q \Pi_{q,\Omega_m})^n}
The sum over n is just the series expansion of a logarithm without the first term, so we add and substract it to get:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\beta \Omega} \simeq Z_0 e^{ - S_{int} } e^{-\frac{1}{2} \displaystyle\sum_{q \neq 0} \displaystyle\sum_m \log(1+V_q \Pi_{q,\Omega_m})-V_q \Pi_{q,\Omega_m}} }
The term outside the logarithm is, if we transform back to imaginary time:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{1}{2}\displaystyle\sum_{-\infty}^{\infty}\displaystyle\sum_{q \neq 0}V_q \beta \Pi_{q,\Omega_n}& =\frac{1}{2}\displaystyle\sum_{q \neq 0}V_q \beta \displaystyle\sum_{k,\sigma,k',\sigma'} \langle \psi^*_{k\sigma}(0^+)\psi_{k-q,\sigma}(0^-) \psi^*_{k'\sigma'}(0^+)\psi_{k'-q,\sigma'}(0^-) \rangle\\ &= -\frac{\beta}{2V} \displaystyle\sum_{q \neq 0} \frac{4 \pi e^2}{q^2} \displaystyle\sum_{k,\sigma} n_F(\epsilon_k) n_F(\epsilon_{k-q}) \end{align}}
Which cancels the 1st order Fock term exactly. So we are left with:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\beta \Omega} \simeq Z_0 e^{-\frac{1}{2} \displaystyle\sum_{q \neq 0} \displaystyle\sum_m \log(1+V_q \Pi_{q,\Omega_m})} }
We can now perform a Hubbard Stratonovich transformation on the action so as to disentangle the products of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_q } 's and perform the integration over grassman variables since the integral is just gaussian. In doing so we introduce new complex (and thus bosonic) fields that interact with the electrons, the Plasmon fields.Performing the integration over the Plasmon fields too we are left with:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{Z}{Z_0}=\displaystyle\prod_{q \neq 0} \displaystyle\prod_n (1+V_q \Pi_{q} (i \Omega_n))}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_{q,\Omega_n}} is the Fourier component of the corellator and is given by the following integral:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_{q,\Omega_n}=-2 \int \frac{d^3k}{(2\pi)^3} \frac{n_F(\epsilon_k)-n_F(\epsilon_{k-q})}{\epsilon_k-\epsilon_{k-q}-i\Omega_n}}
In our case of a Coulomb gas with the unperturbed state being a free fermi gas, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k=\frac{\hbar^2 k^2}{2 m}} . To make the expression more symmetric we can take (since the integration is over all values of k right now) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \rightarrow k+\frac{q}{2}} and get:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_{q,\Omega_n}=-2\int \frac{d^3k}{(2\pi)^3} \frac{n_F(\epsilon_{k+\frac{q}{2}})-n_F(\epsilon_{k-\frac{q}{2}})}{\frac{\vec{k}\cdot \vec{q}}{m}-i\Omega_n}}
Expanding the numerator around Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q=0} and performing the angular integrations the remaining integral is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{(2\pi)^3} \int dk k^2 (2+\tilde{k} \log [ \frac{1-\tilde{k}}{-1-\tilde{k}}] )\frac{\beta}{4 \cosh^2(\frac{\beta}{2} (\frac{k^2}{2m}-\mu))} }
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{k}=\frac{i m \Omega_n}{q k}} . As Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \rightarrow 0} the hyperbolic cosine will become sharply peaked around Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=\sqrt{2 m \mu}=k_F} and thus the main contribution to the integral will be at that value. As such, we evaluate everything else at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F} and notice that the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\beta}{4 \cosh^2(\frac{\beta}{2} (\frac{k^2}{2m}-\mu))}} term came from differentiating a Fermi distribution function. So, from that piece we will get the density of states at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k=\mu} . Expanding the logarithm around small values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{q}{\Omega_n}} we find:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_{q,\Omega_n}=\frac{2}{3}N(\mu) \frac{v^2_F q^2}{\Omega^2_n} }
So now, we look for up to which frequency we can have non-zero values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_{q,\Omega_n}} . Solving, we get:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\Omega_n=\sqrt{\frac{8 \pi e^2}{3} N(\mu)}}
Example: Electron Gas With a Single Impurity
As an example we will derive the partition function for an electron gas inside a three dimensional box with a single impurity. We will assume that the potential created by the atom is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(\textbf{r})} . The Hamiltonian describing this system is given as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{k\sigma}(\epsilon_{k} - \mu) \psi_{k\sigma}^{\dagger} \psi_{k\sigma} + \frac{1}{2V}\sum_{q \neq 0} \frac{4\pi e^{2}}{q}\sum_{k\sigma}\sum_{k'\sigma'}\psi_{k\sigma}^{\dagger} \psi_{k'\sigma'}^{\dagger} \psi_{k'+q \sigma'} \psi_{k - q\sigma}+\frac{1}{V}\sum_{q} U_{q}\sum_{k\sigma}\psi_{k\sigma}^{\dagger}\psi_{k -q\sigma}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{k}=\frac{k^{2}}{2m}} .
An expression for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{q} } in terms of the potential generated by the impurity can be obtained through Fourier transforming the fields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi^{\dagger}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi } .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\sigma} \int d^{3}r U(r) \psi_{\sigma}^{\dagger}(r) \psi_{\sigma}(r)=\sum_{\sigma} \int d^{3}r U(r) \sum_{k}e^{-ikr}\psi_{k\sigma}\sum_{k'}e^{ik'r}\psi_{k'\sigma} }
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q=k - k' \rightarrow k' = k - q} . Then
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{\sigma}\int d^{3}r U(r) \frac{1}{V} \sum_{k} \sum_{q}\psi_{k \sigma}^{\dagger}\psi_{k-q \sigma} = \frac{1}{V}\sum_{q}(\int d^{3}r e^{-iqr} U(r))\sum_{k\sigma}\psi_{k\sigma}^{\dagger}\psi_{k - q \sigma} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \implies U_{q} = \int d^{3}r e^{-iqr} U(r) }
Now we wish to derive an expression for the grand canonical partion function using the Fermionic coherent state path integral formalism. The starting point is to write down the path integral with interaction terms from the well known expression derived previously. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z = \int D(\psi^{*} , \psi) e^{- S(\psi^{*} , \psi)} = Z_{0}\int D(\psi^{*} , \psi) e^{- S_{int}(\psi^{*} , \psi)}}
where we have made the following identifications
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{0}= \int_{0}^{\beta} d\tau \sum_{k\sigma}(\epsilon_{k}-\mu)\psi_{k\sigma}^{\dagger}(\tau) \psi_{k\sigma}(\tau) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{int} = \int_{0}^{\beta} d\tau \frac{1}{2V}\sum_{q \neq 0} \frac{4\pi e^{2}}{q}n_{-q}(\tau)n_{q}(\tau)+\frac{1}{V}\sum_{q}U_{q}n_{-q}(\tau) }
and define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{q} \equiv \sum_{k \sigma}\psi_{k\sigma}^{\dagger}\psi_{k +q \sigma}} .
Now we wish to evaluate the interaction component of the path integral. We do this by expressing it as a double coherent state path integral over both the Grassman Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{k\sigma}(\tau)}
and complex fields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{q}(\tau)}
. We start by rewriting the terms of the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\frac{\Delta \tau}{2V} \frac{4\pi e^{2}}{q}n_{-q}(\tau)n_{q}(\tau)}}
for every time slice using the familiar identity
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\frac{1}{a}J^{*}J}=\frac{\int d\phi^{*} d\phi e^{-a\phi^{*}\phi} e^{iJ^{*}\phi} e^{i\phi^{*}J}}{\int d\phi^{*} d\phi e^{-a\phi^{*}\phi}}. }
The following identifications Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J^{*}=\frac{\Delta \tau}{2V} \frac{1}{V_{q}}n_{-q}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J=\frac{\Delta \tau}{2V} \frac{1}{V_{q}}n_{q}} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=\frac{\Delta \tau}{2V} \frac{1}{V_{q}}} lead to
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \implies const \cdot \int \prod_{q} d\phi_{q} e^{-\int_{0}^{\beta} d\tau \frac{1}{2V} \sum_{q \neq 0} \phi_{-q}(\tau)\frac{1}{V_{q}} \phi_{q}(\tau)} e^{i \int_{0}^{\beta} d\tau \frac{1}{V} \sum_{q \neq 0} \phi_{-q}n_{q}(\tau)}e^{\int_{0}^{\beta} d\tau\frac{1}{V}\sum_{q \neq 0} U_{-q}n_{q}(\tau)}}
So we have an integral over both the fields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{kσ}(\tau)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{q}(\tau) } .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{int} = const \cdot \int \prod_{q} d\phi_{q} e^{-\int_{0}^{\beta} d\tau \frac{1}{2V} \sum_{q \neq 0} \phi_{-q}(\tau)\frac{1}{V_{q}} \phi_{q}(\tau)} \langle e^{i \int_{0}^{\beta} d\tau \frac{1}{V} \sum_{q \neq 0} \phi_{-q}n_{q}(\tau)}e^{\int_{0}^{\beta} d\tau\frac{1}{V}\sum_{q \neq 0} U_{-q}n_{q}(\tau)}\rangle_{0} }
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{q}(\tau) = \frac{1}{\beta} \sum_{\Omega_{n}} e^{-i\Omega_{n}\tau}\Phi_{q}(i\Omega_{n}) } then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{\beta} d\tau e^{i\Omega_{n}\tau} \phi_{q}(\tau) = \Phi_{q}(i\Omega_{n})} . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \implies U_{-q}(i\Omega_{n}) = \int_{0}^{\beta} d\tau e^{i\Omega_{n}\tau} U_{-q} = U_{-q} \beta \delta_{\Omega_{n},0}}
The term Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle..\rangle_{0}} can be calculated using a Cummulant expansion to second order in powers of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} . This expansion is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{0}\langle e^{-S_{int}} \rangle = Z_{0}e^{-\langle S_{int}\rangle}e^{\frac{1}{2}\langle S_{int}^{2}\rangle - \langle S_{int}\rangle^{2}} }
and leads to the following once the thermal averages have been evaluated.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \implies \int \prod_{q} d \Phi_{q} e^{-\frac{1}{2\beta}\sum_{\Omega_{n}} \int \frac{d^{3}q}{2\pi^{3}}(\Phi_{-q}(-i\Omega_{n})\Phi_{q}(i\Omega_{n}) \frac{1}{V_{q}} + (\Phi_{-q}(-i\Omega_{n})+ iU_{-q}(-i\Omega_{n}))\Pi_{q}(i\Omega_{n})(\Phi_{q}(i\Omega_{n})+iU_{q}(i\Omega_{n}))} }
Integrating out the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} fields gives the following
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = e^{\frac{1}{2\beta}\sum_{\Omega_{n}}\int \frac{d^{3}q}{2\pi^{3}}[\Pi_{q}(i\Omega_{n})-\frac{\Pi_{q}(i\Omega_{n})^{2}}{\frac{1}{V_{q}}+\Pi_{q}(i\Omega_{n})}]U_{-q}(-i\Omega_{n})U_{q}(i\Omega_{n})} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =e^{\frac{1}{2\beta}\frac{1}{V} \sum_{q \neq 0} \frac{\frac{1}{V_{q}}\Pi_{q}(i\Omega_{n}=0)}{\frac{1}{V_{q}}+\Pi_{q}(i\Omega_{n}=0)}\beta^{2}U_{-q}U_{q}} }
Thus, the partition function within this approximation is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z \approx const \cdot Z_{0} e^{\frac{1}{2}\beta \frac{1}{V} \sum_{q \neq 0} \frac{\Pi_{q}(i\Omega_{n}=0)}{1+V_{q}\Pi_{q}(i\Omega_{n}=0)}U_{-q}U_{q}} }
Individual Wiki Projects
Lattice Gas Model of Liquid Helium
Double-layer Quantum Hall Ferromagnets
scaling theory of localization
Renormalization Group (RG) Approach to Interacting Fermions
Effective field theory and RG approach to interacting Fermions
Bose-Einstein Condensation in Spin-gaped Systems
Random Phase Approximation for the Collective Modes of Nuclei
Bethe Ansatz for Many-Particle Systems
Charge Density Wave (CDW) State in Hubbard Model in Zero Temperature