Talk:Phy5670

Collective Modes in Non-symmetry Breaking Systems

Sound waves propagating through air or water are examples for collective modes. Such modes arise in media that don't break symmetry, such as ordinary gases and fluids. Those waves typically have wavelengths that are very large compared to the distance between neighboring particles, which is the reason why we will look at very small wave vectors. An example for a collective mode due to broken symmetry is a shear mode in a solid.
Recall that the partition function can be written as the Feynman path integral

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z = \int D(c^{*}, c) e^{-S}, }

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_0 = \frac{1}{\beta} \sum_{\omega_n} \sum_{k}(-i\omega_n + \epsilon_n-\mu) c_{k,\sigma}^{*} c_{k,\sigma}(\omega_n) }

is the action of the non-interacting system; while the action of the interacting system is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{int} = \frac1{\beta} \sum_{\Omega_n} \frac1{L^3}\sum_{q} V_q n_{-q}(-i\Omega_n) n_q(i\Omega_n) }

with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_q (i\Omega_n) = \frac1{\beta}\sum_{\omega_n}\sum_k c^*_{k+q, \sigma} (i\omega_n + i\Omega_n) c_{k,\sigma}(i \omega_n) }

The partition function can be calculated via the Hubbard-Stratonovich Transformation, which can be motivated by the one-dimensional integral

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 = \frac1{\sqrt{\pi a}}\int\limits_{-\infin}^{\infin}dx e^{-\frac1a x^2}. }

The pre-factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\pi a} } is simply the constant number that equals to the value of the integral.
In the language of path integrals this implies

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 = \frac1N \int D(\phi(r,\tau)) e^{ -\int\limits_0^{\beta}d\tau \int d^3r \phi_{-q}(r)V^{-1}(r-r')\phi_q(r') }. }

Here the number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} resembles the pre-factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{\pi a} } in the given example. Rewriting the potential in momentum space, this identity allows to convert the partition function. This is done by a shift of the field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_q(i\Omega_n)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_q(i\Omega_n) = \tilde{\phi}_q(i\Omega_n) + i V_q n_q(i\Omega_n).}

The partition function, as introduced at the beginning of this chapter, simplifies thereby to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} Z &= 1 \cdot \int D(c^*,c) e^{-S} \\ &= \frac1{N} \int D\phi_q(i\Omega_n)e^{ -\frac1{\beta} \sum_{\Omega_n}\frac1{L^3}\sum_q \phi_{-q}(-i \Omega_n) \frac1{V_q} \phi_q(i\Omega_n)} \cdot \int D(c^*,c) e^{-S} \\ &\simeq Z_0 \int D\tilde\phi_q(i\Omega_n) \left[ \int D(c^*,c) e^{-S_0} e^{-\frac1{\beta}\sum_{\Omega_n} \frac1{L^3}\sum_q 2i n_{-q}(-i\Omega_n) \tilde \phi_q(i\Omega_n)}\frac1{Z_0} \right] e^{-\frac1{\beta}\sum\frac1{L^3}\sum_q \frac{\tilde\phi_{-q}(-i\Omega_n)\tilde\phi_{q}(i\Omega_n)}{V_q}}\\ &= \left\langle e^{-\frac1{\beta}\sum_{\Omega_n} \frac1{L^3}\sum_q 2i n_{-q} \tilde\phi_q(i\Omega_n)}\right\rangle\\ &\equiv \left\langle e^A\right\rangle \end{align}}

This can be calculated by a cumulant expansion, such that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} Z &= \left\langle e^A \right \rangle_0 \\ &= e^{\langle A \rangle_0 + \frac12 \left( \langle A^2 \rangle_0 -0 \langle A \rangle^2 \right) + \ldots} \end{align} }

Now, since the the average of the density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_q(i\Omega_n)} is equal to zero, i.e.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle n_q(i\Omega_n)\right\rangle = 0, \quad \forall q\neq 0 \and \Omega_n\neq 0, }

we only have to calculate the term with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle A^2\rangle} in the exponent. This term contains the average of two density operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_q(i\Omega_n)} , which can be evaluated using the Wick's theorem.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n_{-q}(-i\Omega_n)n_{q'}(i\Omega_n')\rangle = \frac1{\beta^2} \sum_{\omega_n,\omega_n'} \sum_{k,k'} \langle c^*_{k-q,\sigma}(i\omega_n-i\Omega_n)c_{k,\sigma}(i\omega_n) c^*_{k'+q',\sigma'}(i\omega_n'+i\Omega_n')c_{k',\sigma'}(i\omega_n') \rangle_0 }

Since there are two creation operators and two annihilation operators, only two contractions are possible. However, one of these contractions is a non-connected Feynman diagram and so, according to the linked cluster theorem, we only have to consider the connected one. Due to Kronecker-delta symbols (arising from the contractions) we will be left with only one sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} and one sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} . The resulting sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} can be written as an integral over a continuum (by taking the appropriate limit of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L\rightarrow\infin} ), while the sum over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} is written as a contour integral. The result of this exercise is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac Z{Z_0} \simeq \int D\phi e^{S_{eff}(\phi)}, }

where the effective action is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{eff}(\phi) = \frac1{\beta}\sum_{\Omega_n}\frac1{L^3} \sum_q\left(\frac1{V_q}-2 \mathcal N\Pi_q(i\Omega_n) \right) \phi_{-q}(i\Omega_n) \phi_q(i\Omega_n) + \mathcal O(\phi^4).}

Here we use the degeneracy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}} of each level. This action is expressed in terms of an integral that we are about to solve, namely

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_q(i\Omega_n) = \int \frac{d^3k}{(2\pi)^3} \frac{n_F(\epsilon_k)-n_F(\epsilon_{k-q})} {\epsilon_k - \epsilon_{k-q}-i\Omega_n}. }

In this expression Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_F(E)=\frac1{e^{\frac{E-\mu}{kT}+1}}} is the Fermi-Dirac distribution, together with the chemical potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , the Boltzmann factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B} and the temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} .

As said before, our special interest is pointed towards density waves in an electron gas. So finally, the degeneracy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}} will be set equal to 2. Notice that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_q(i\Omega_n)} couples to density.
We also said in the beginning of the chapter that wavelengths of such excitations are typically very long compared to the distance between molecules; or, in case of a plasma, the distance between electrons. Therefore, when we calculate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_q(i\Omega_n)} we look at the limit of very small wave vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} , and we will also consider small temperatures. For an electron gas the energy dispersion is, of course, quadratic in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} , being Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k=\frac{\hbar^2k^2}{2m}} .

Therefore, let us assume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |q|\ll k_F} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T\ll \mu} .
In that case the difference

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} n_F(\epsilon_k)-n_F(\epsilon_{k-q}) \end{align}}

in the integrand of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_q(i\Omega_n)} has no contribution for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_k} being far away from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_F} . Hence we can expand the numerator of the integrand by writing

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} n_F(\epsilon_{k-q}) &= n_F(\epsilon_{k}+\epsilon_{k-q}-\epsilon_{k})\\ &\simeq n_F(\epsilon_k) + n_F'(\epsilon_k) (\epsilon_{k-q} - \epsilon_k). \end{align} }

With this approximation the quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Pi_q(i\Omega_n)} can be calculated via the Sommerfeld expansion, i.e. after integration over the angles we multiply the expression by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1=\int\limits_{-\infin}^{\infin}d\epsilon \delta(\epsilon-\epsilon_F)} and exchange the integrals over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} . Roughly speaking, the integral over k equals the density of states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N(\epsilon)} . Notice that we add Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0=-i\Omega_n+i\Omega_n} to the numerator of the integrand. The calculation is as follows.

${\begin{aligned}\Pi _{q}(i\Omega _{n})&=\Pi _{q}(i\Omega _{n})=\int {\frac {d^{3}k}{(2\pi )^{3}}}{\frac {(n_{F}(\epsilon _{k})-n_{F}(\epsilon _{k-q})-i\Omega _{n})+i\Omega _{n}}{\epsilon _{k}-\epsilon _{k-q}-i\Omega _{n}}}.\\&=\Pi _{q}(i\Omega _{n})=\int {\frac {d^{3}k}{(2\pi )^{3}}}(1+{\frac {i\Omega _{n}}{{\frac {\hbar ^{2}k^{2}}{2m}}-{\frac {\hbar ^{2}}{2m}}(k-q)^{2}-i\Omega _{n}}})\\&=\Pi _{q}(i\Omega _{n})=\int {\frac {d^{3}k}{(2\pi )^{3}}}(1+{\frac {i\Omega _{n}}{{\frac {\hbar ^{2}}{2m}}kq\cos(\theta )-{\frac {\hbar ^{2}q^{2}}{2m}}-i\Omega _{n}}})\\&=\int \limits _{-\infty }^{\infty }d\epsilon N(\epsilon )n_{F}'(\epsilon )\left(1+{\frac {i\Omega _{n}}{2v_{F}\hbar q}}\ln {\frac {v_{F}\hbar q-i\Omega _{n}}{-v_{F}\hbar q-i\Omega _{n}}}\right)\\&=-N(\epsilon _{F})\left(1+{\frac {i\Omega _{n}}{2v_{F}\hbar q}}\ln \left({\frac {i\Omega _{n}-v_{F}\hbar q}{i\Omega _{n}+v_{F}\hbar q}}\right)\right).\end{aligned}}$

The last step uses that in the low-temperature limit the derivative of the Fermi distribution function $n_{F}'(\epsilon )$ only has a contribution at $\epsilon =\epsilon _{F}$, where it is sharply peaked. We introduced the Fermi velocity $v_{F}=\hbar k_{F}/m$, which is the velocity of Fermions that are right on the Fermi surface.

Now, the expression

${\frac {1}{V_{q}}}-2{\mathcal {N}}\Pi _{q}(i\Omega _{n})$

(in the effective action $S_{eff}$ defined above) is the inverse of a Green's function. So in order to get knowledge of the spectrum of the system, we seek the zeros of this expression. This is shown in the next subsection.

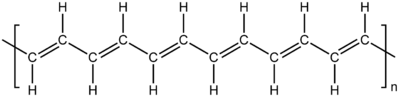
Dimerization in Polyacetylene

Polyacetylene is an organic compound that consists of 1D polymer chain of carbon and hydrogen atoms as the lattice points and branches. The structure is basically repetitions of acetylene molecule $(C_{2}H_{2})$ and produces a high electrical conductivity. The interesting part of it is its alternating bonds between single and double ones and will produce a small energy gap within its spectrum band. The energy band makes it behave as a good semi-conductor material which we can practically use as electronic components.

(The structure of Polyacetylene); http://upload.wikimedia.org/wikipedia/commons/thumb/5/58/Trans-(CH)n.png/400px-Trans-(CH)n.png

Now let's trace how polyacetylene can create such energy gap. First, we assume the chain as 1D lattice chain that contains dimers constructed by alternating bond types. This means that the electron jumps with different probabilities between the sites. The double bond jump is more probable than the single one since it needs lower energy to apply. In addition to that, we also consider the "stifness" and kinetic energy factor. By taking all of these relevant compositions, the Hamiltonian of the chain becomes,

${\mathcal {H}}=\sum _{j}{\frac {m}{2}}{{\dot {u}}_{j}}^{2}+\sum _{j}{\frac {\kappa }{2}}(u_{j+1}-u_{j})^{2}-\sum _{js}(t_{j+1,j}{c_{j+1,s}}^{\dagger }c_{j,s}+h.c)$

$t_{n+1,n}=t_{o}-\alpha (u_{n+1}-u_{n})$

Some simplifications can be made by getting rid of the kinetic term cause the mass is relatively too big for the detail energy dynamics. Then we can assume 2 interdependent fixed energies of hopping term, means the single bond expands with a certain number from equilibrium while the double bond contracts with the same number

$u_{j}=\pm (-1)^{n}u_{o}$

${\begin{aligned}t_{j+1,j}&\Rightarrow t_{o}-t_{1}......single\\&\Rightarrow t_{o}+t_{1}......double\end{aligned}}$

This difference creates dimers model and so we can separate the lattice into 2 which are the odd and even parts with half filling for each. Then we can rewrite the Hamiltonian as,

${\mathcal {H}}=\sum _{j}{\frac {\kappa }{2}}(u_{j+1}-u_{j})^{2}-(t_{o}-t_{1})\sum _{js}^{N/2}({c_{2j-1,s}}^{\dagger }c_{2j,s}+h.c)-(t_{o}+t_{1})\sum _{js}^{N/2}({c_{2j+1,s}}^{\dagger }c_{2j,s}+h.c)$

Now, we want to couple all separate sites as few modes. That's why we have to Fourier transform the creation and annihilation operators form lattice space to momentum space.

$a_{2j-1,s}={\sqrt {\frac {2}{N}}}\sum _{k=1}^{N/2}e^{i{\frac {2\pi }{N}}k(2j-1)}a_{s}(k)$

$b_{2j,s}={\sqrt {\frac {2}{N}}}\sum _{k=1}^{N/2}e^{i{\frac {2\pi }{N}}k(2j)}b_{s}(k)$

These new operators already commute to each other. Let's replace both inside the Hamiltonian as,

${\begin{aligned}{\mathcal {H}}_{hop}&=-(t_{o}-t_{1})\sum _{s,k=1}^{N/2}(e^{i{\frac {2\pi }{N}}k}{a_{s}(k)}^{\dagger }b_{s}(k)+h.c)-(t_{o}+t_{1})\sum _{js}^{N/2}(e^{-i{\frac {2\pi }{N}}k}{a_{s}(k)}^{\dagger }b_{s}(k)+h.c)\\&=-\sum _{s,k=1}^{N/2}[2t_{o}cos({\frac {2\pi }{N}}k)-2t_{1}sin({\frac {2\pi }{N}}k)]{a_{s}(k)}^{\dagger }b_{s}(k)-\sum _{s,k=1}^{N/2}[2t_{o}cos({\frac {2\pi }{N}}k)+2t_{1}sin({\frac {2\pi }{N}}k)]{b_{s}(k)}^{\dagger }a_{s}(k)\\\end{aligned}}$

By doing matrix rearrangement and diagonalize it, we get 2 modes of single particle excitation spectrum which is,

$\epsilon (k)=\pm 2t_{o}{\sqrt {{cos}^{2}({\frac {2\pi }{N}}k)-({\frac {t_{1}}{t_{o}}})^{2}{sin}^{2}({\frac {2\pi }{N}}k)}}$

If we plot this spectrum we'll get the maximum width between 2 modes and their gap which are equal to $4t_{o}\approx 10eV$ and $4t_{1}\approx 1.4eV$. Finally we need to discuss some structure possibilities of polyacetylene. It can have cis or trans molecule which are mirrored with each other or could even be a mix of them. If it is so, then there will be a boundary in between which we call it domain wall, behaving like a localized, stable, and dynamic soliton. A neutral soliton is proposed to be one bond length unpaired spin wall that makes it harder to move to other sites. Nowadays, the focus of polyacetylene research is the wide-range control possibility of the doped one. This doping might come from charged domain walls since it shows some interesting properties like anomalous magnetic susceptibility, infrared absorbtion, and power from temperature.