Phy5645/Double pinhole experiment: Difference between revisions

Latest revision as of 13:20, 18 January 2014

(a) As stated in the problem, we assume that the denominators are approximately the same between the two waves. This is justified because the corrections are only on the order of $d/L\!$ , and we are interested in the case where $d<<L\!$ . We require that the numerators have the same phase, namely $kr_{+}-kr_{-}=2\pi n\!$ . We expand the LHS with respect to $d\!$ ,

{\begin{aligned}k(r_{+}-r_{-})&\approx k\left\{\left({\sqrt {L^{2}+x^{2}+y^{2}}}+{\frac {yd}{2{\sqrt {L^{2}+x^{2}+y^{2}}}}}\right)\right.\\&-\left.\left({\sqrt {L^{2}+x^{2}+y^{2}}}-{\frac {yd}{2{\sqrt {L^{2}+x^{2}+y^{2}}}}}\right)\right\}\\&=k{\frac {dy}{\sqrt {L^{2}+x^{2}+y^{2}}}}\end{aligned}}

Therefore, $k{\frac {dy}{\sqrt {L^{2}+x^{2}+y^{2}}}}=2\pi n\!$

and hence

{\frac {y}{\sqrt {L^{2}+x^{2}+y^{2}}}}=n{\frac {\lambda }{d}}\!

(b) Let us work in units in which $k=1$ ; that is, we measure all lengths in units of $1/k\!$ . We then set $d=20\!$ and $L=1000\!$ . Here is the interference pattern. We first plot the pattern along the $y\!$ axis $(x=0):\!$

(c) Using the same parameters as before, we now plot the pattern on the $xy\!$ plane:

(d) We use the same parameters as in (b) and (c). First, we plot the pattern along the $y\!$ axis $(x=0):\!$

We now plot the pattern on the plane:

The main difference is the absence of the interference pattern.

Back to Stern-Gerlach Experiment

@@ Line 1: / Line 1: @@
-Submitted by team 1
+(a) As stated in the problem, we assume that the denominators are approximately the same between the two waves. This is justified because the corrections are only on the order of <math>d/L\!</math>, and we are interested in the case where <math>d<<L\!</math>. We require that the numerators have the same phase, namely <math>kr_{+}-kr_{-}=2\pi n\!</math>. We expand the LHS with respect to <math>d\!</math>,
-------
-'''Question: Double Pinhole Experiment'''
-Besides the Stern-Gerlach experiment, the double slit experiment also demonstrates the difference between quantum mechanics and classical mechanics.  Here, we will discuss a double pinhole experiment rather than a double slit experiment because the former is mathematically simpler and still embodies the basic physics that we wish to demonstrate.
-[[Image:Double_pinhole_1.JPG]]
-Suppose that a beam of electrons, traveling along the <math>z</math> axis, hits a screen at <math>z = 0</math> with two pinholes at <math>x = 0, y = \pm d/2</math>. For a point <math>(x,y)</math> on a second screen at <math>z = L>>d, \lambda</math>, the distance from each pinhole is given by <math> r_{\pm}=\sqrt{x^{2}+(y\mp d/2)^{2}+L^{2}}</math>.  A spherical wave is emitted from each pinhole; the waves from each add, and the wave function at a given point on the second screen is
-:<math>\psi(x,y)=\frac{e^{ikr_{+}}}{r_{+}}+\frac{e^{ikr_{-}}}{r_{-}},</math>
-where <math> k = 2\pi /\lambda .</math>
-(a) Considering just the exponential factors, show that the constructive interference appears approximately at
-:<math> \frac{y}{r}=n\frac{\lambda}{d}</math>
-where <math> r=\sqrt{x^{2}+y^{2}+L^{2}}.</math>
-(b) Make a plot of the intensity <math>|\psi(0,y)|^{2}</math> as a function of <math>y</math>, by choosing <math>k=1, d =20</math>, and <math> L=1000. </math>  The intensity <math>|\psi(0,y)|^{2}</math> is interpreted as the probability distribution for the electron to be detected on the screen, after repeating the same experiment many many times.
-(c) Make a contour plot of the intensity <math>|\psi(x,y)|^{2}</math> as a function of <math>x</math> and <math>y</math>, for the same parameters.
-(d) If you place a counter at both pinholes to see if the electron has passed one of them, all of a sudden the wave function "collapses". If the electron is observed to pass through the pinhole at <math>y=+d/2\!</math>, the wave function becomes
-:<math>\psi_{+}(x,y)=\frac{e^{ikr_{+}}}{r_{+}}.</math>
-If it is observed to pass through that at <math>y=-d/2\!</math>, the wave function becomes
-:<math>\psi_{-}(x,y)=\frac{e^{ikr_{-}}}{r_{-}}.</math>
-After repeating this experiment many times with 50:50 probability for each the pinholes, the probability on the screen will be given by
-:<math>|\psi_{+}(x,y)|^{2}+|\psi_{-}(x,y)|^{2}\!</math>
-instead. Plot this function on y-axis, and also show the contour plot, to compare its pattern to the case when you do not place a counter. What is the difference from the case without the counter?
---------
-'''Answer:'''
-(a) As directed, we assume that the denominators are approximately the same between two waves. This is justified because the corrections are only of the order of <math>d/l\!</math>, and we are interested in the case where <math>d<<L\!</math>. We require that the numerators have the same phase, namely <math>kr_{+}-kr_{-}=2\pi n\!</math>. We expand the LHS with respect to <math>d\!</math>,
 :<math>
@@ Line 63: / Line 16: @@
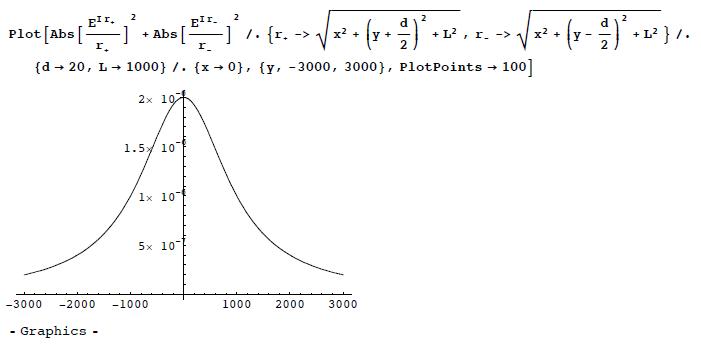
-(b) Let us choose the unit where ''k'' = 1. Then we pick ''d'' = 20, ''L'' = 1000. Here is the interference pattern. First along the ''y''-axis (''x'' = 0):
+(b) Let us work in units in which <math>k = 1</math>; that is, we measure all lengths in units of <math>1/k\!</math>. We then set <math>d = 20\!</math> and <math>L = 1000\!</math>. Here is the interference pattern. We first plot the pattern along the <math>y\!</math> axis <math>(x = 0):\!</math>
@@ Line 69: / Line 22: @@
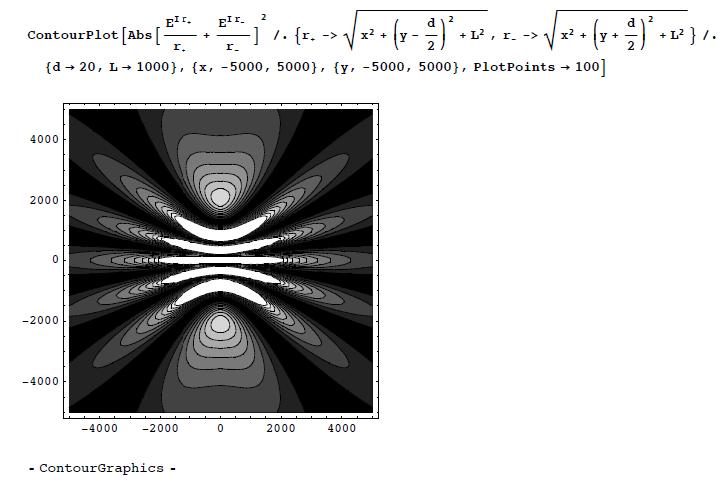
-(c) Now on the plane:
+(c) Using the same parameters as before, we now plot the pattern on the <math>xy\!</math> plane:
 [[Image:Double_pinhole_plot_2.JPG]]
-(d) For the same parameter as in (b), First along the ''y''-axis (''x'' = 0):
+(d) We use the same parameters as in (b) and (c).  First, we plot the pattern along the <math>y\!</math> axis <math>(x = 0):\!</math>
 [[Image:Double_pinhole_plot_3.JPG]]
+We now plot the pattern on the plane:
-Now on the plane:
 [[Image:Double_pinhole_plot_4.JPG]]
+The main difference is the absence of the interference pattern.
-The main difference is the absence of the interference pattern.
+Back to [[Stern-Gerlach Experiment#Problem|Stern-Gerlach Experiment]]

Phy5645/Double pinhole experiment: Difference between revisions

Latest revision as of 13:20, 18 January 2014

Navigation menu

Search