Solution to Set 4: Difference between revisions
HollyBrown (talk | contribs) No edit summary |
|||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 33: | Line 33: | ||
Draw the planes whose Miller indices are (421), (112), (1-10) and (-121). State their intercepts on the x- y- and z- axes. | Draw the planes whose Miller indices are (421), (112), (1-10) and (-121). State their intercepts on the x- y- and z- axes. | ||
Miller indicies are used as a way to note planes and directions in crystal lattices. To graph the miller indicies in a cartesian coordinate system, you can use the equation <math>1/Miller Index = Intercept</math> | |||
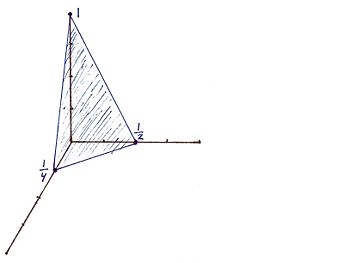
For the Miller indicies (421) the x, y, and z intercepts are respectively (1/4, 1/2, 1). This gives rise to the graph | |||
[[Image:Miller_Indicies_1.jpg|frameless|350px]] | |||
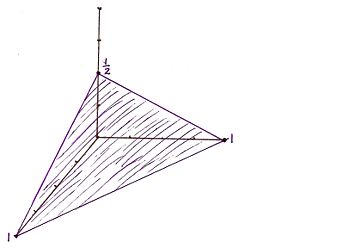
For the Miller indicies (112) the x, y, and z intercepts are respectively (1, 1, 1/2). This gives rise to the graph | |||
[[Image:Miller_Indicies_3.jpg|frameless|350px]] | |||
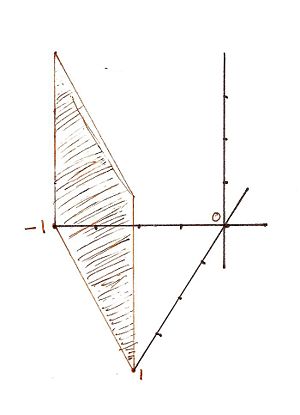
For the Miller indicies ( | For the Miller indicies (1-10) the x, y, and z intercepts are respectively (1, -1, 0) meaning that there is no intercept on the z axis. This gives rise to the graph | ||
[[Image:Miller_Indicies_2.jpg|frameless|300px]] | |||
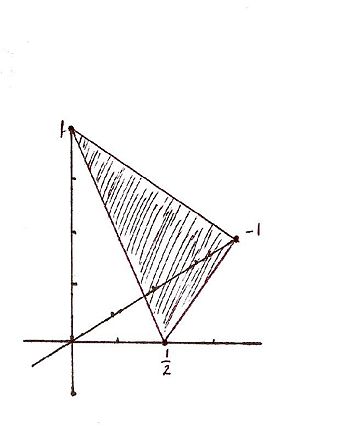
For the Miller indicies (-121) the x, y, and z intercepts are respectively (-1, 1/2, 1). This gives rise to the graph | For the Miller indicies (-121) the x, y, and z intercepts are respectively (-1, 1/2, 1). This gives rise to the graph | ||
[[Image:Miller_Indicies_4.jpg|frameless|350px]] | |||
==Problem 3== | ==Problem 3== | ||
| Line 60: | Line 64: | ||
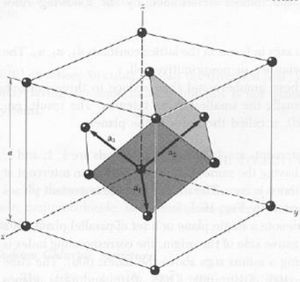
'''c.''' | '''c.''' The FCC cell has 4 atoms in it. Each vertex is 1/4 of an atom, and each face cell is 1/2 an atom in the cell. The Primitive Cell has 1 atom in it as it is the smallest possible cell to get. Each vertex of it has 1/8 of an atom on it. | ||
Latest revision as of 21:01, 29 April 2009
Problem 1
Cu, density , atomic mass , fcc structure
a. In , the number of moles is
b. Atoms in
c. Since the bonds between the atoms are small compared to the diameter of the atom, we neglect the bonds for an estimate. The structure is fcc and the length of each side of the cube is , where r is the radius of one Cu atom.
d. Atomic radius
, where
e. Mass of 1 atom
Problem 2
Draw the planes whose Miller indices are (421), (112), (1-10) and (-121). State their intercepts on the x- y- and z- axes.
Miller indicies are used as a way to note planes and directions in crystal lattices. To graph the miller indicies in a cartesian coordinate system, you can use the equation
For the Miller indicies (421) the x, y, and z intercepts are respectively (1/4, 1/2, 1). This gives rise to the graph
For the Miller indicies (112) the x, y, and z intercepts are respectively (1, 1, 1/2). This gives rise to the graph
For the Miller indicies (1-10) the x, y, and z intercepts are respectively (1, -1, 0) meaning that there is no intercept on the z axis. This gives rise to the graph
For the Miller indicies (-121) the x, y, and z intercepts are respectively (-1, 1/2, 1). This gives rise to the graph
Problem 3
a. fcc and primitive cell
b.
The volume of the primitive cell is the volume of the fcc cell.
c. The FCC cell has 4 atoms in it. Each vertex is 1/4 of an atom, and each face cell is 1/2 an atom in the cell. The Primitive Cell has 1 atom in it as it is the smallest possible cell to get. Each vertex of it has 1/8 of an atom on it.