Homeworks 3: Difference between revisions
No edit summary |
|||
| (5 intermediate revisions by one other user not shown) | |||
| Line 71: | Line 71: | ||
===Catadioptric Telescope=== | ===Catadioptric Telescope=== | ||
Catadioptric telescopes like the Schmidt telescope provide a wide-angle field of view and thus are often used as cameras. However, they suffer from both spherical and chromatic aberration. | Catadioptric telescopes like the Schmidt telescope provide a wide-angle field of view and thus are often used as cameras. They can designed for wide field views because two more surfaces allow higher order corrections. However, they suffer from both spherical and chromatic aberration. | ||
==Problem 3== | ==Problem 3== | ||
| Line 102: | Line 102: | ||
compare it to the size (in arc-sec) of an extended object, and remember your PHY2048/9). | compare it to the size (in arc-sec) of an extended object, and remember your PHY2048/9). | ||
[[Image: | [[Image:Diagram.jpg|thumb|center|530px|The diagram has been exaggerated to show the geometric relations.]] | ||
We all know that for small angles, | We all know that for small angles, | ||
| Line 110: | Line 110: | ||
Where f is the focal length and R is the radius of curvature for a spherical mirror. The problem is that with large angles, the foci will not match up, causing the aberration. | Where f is the focal length and R is the radius of curvature for a spherical mirror. The problem is that with large angles, the foci will not match up, causing the aberration. | ||
For large angles, | For large angles, the focal length can be written as, | ||
<math> f'=x+y </math> | <math> f'=x+y </math> | ||
and the angles can be determined directly through trigonometric relations from the diagram. They are, | |||
<math> \cos{\phi}=\frac{R-y}{R} </math> and | <math> \cos{\phi}=\frac{R-y}{R} </math> and | ||
| Line 136: | Line 137: | ||
<math> z=\sqrt{R^2+h^2}-\frac{R^2-2h^2}{2\sqrt{R^2-h^2}}-\frac{R}{2} </math> | <math> z=\sqrt{R^2+h^2}-\frac{R^2-2h^2}{2\sqrt{R^2-h^2}}-\frac{R}{2} </math> | ||
This z is | This z is one of the ways to calculate the size of the spherical aberration, but it is dependent on h. Normally we know things like the focal length and the radius of curvature so I cannot directly find the numerical value of the aberration, but derivation of a similar equation based on the horizontal distance h' from R/2 to the reflected light ray being dependent on the focal length would give a value given our constants. | ||
Also, just as check, it can easily be seen that in the limit as <math> h->0 </math>, z reduces to the expected result of zero. | Also, just as check, it can easily be seen that in the limit as <math> h->0 </math>, z reduces to the expected result of zero. | ||
Latest revision as of 17:25, 1 October 2009
Homework 3 due on 09/21/2009
Problem 1
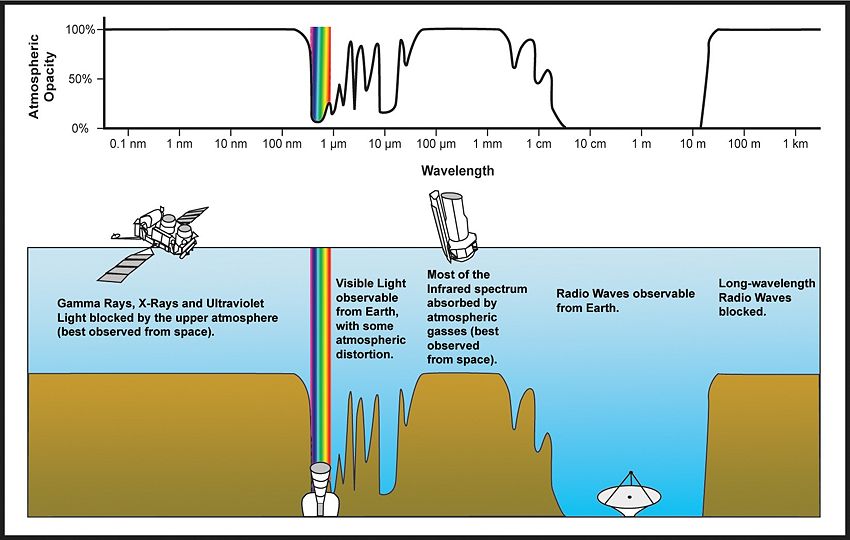
For each of the following types of electromagnetic radiation give a typical wavelength and state whether it can penetrate the Earth’s atmosphere: radio, microwave, infrared, visible, ultraviolet, X-ray, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} -ray.
| Wavelength | Wavelength Range | Does it penetrate Earth's Atmosphere? |
|---|---|---|
| Radio | 10 m - Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^8} m | From ~10 m to ~20 m, yes |
| Microwave | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-3}} m - 10 m | Some is absorbed at smaller wavelengths |
| Infrared | 700 nm - Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-3}} m | Most are absorbed by atmospheric gasses |
| Visable | 400 nm - 700 nm | Yes, with some distortion |
| Ultraviolet | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-8}} m - 400 nm | No, all incoming rays are blocked |
| X-Ray | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-11}} m - Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-8}} m | No, all incoming rays are blocked |
| Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} -ray | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-17}} m - Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-11}} m | No, all incoming rays are blocked |
Problem 2
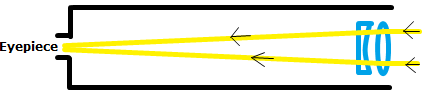
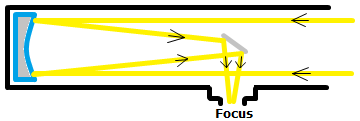
Sketch the typical light path of reflector and refractor telescopes, and name two of the advantages and disadvantages for each of the designs. Catadioptric designs such as the Maksukov and Schmidt telescopes have both a primary lense and a mirror. Name the main advantage and drawback of these designs, and their main application.
Refraction Telescope
| Advantages | Disadvantages |
|---|---|
| High resolution | Large objective lenses deform under gravity. |
| No incoming light is blocked. | Chromatic aberration |
Reflection Telescope
| Advantages | Disadvantages |
|---|---|
| No chromatic aberration | The prime focus is in the path of incoming light. |
| Only the reflecting surface needs to be polished to perfection. | Large detectors produce a lot of torque. |
Catadioptric Telescope
Catadioptric telescopes like the Schmidt telescope provide a wide-angle field of view and thus are often used as cameras. They can designed for wide field views because two more surfaces allow higher order corrections. However, they suffer from both spherical and chromatic aberration.
Problem 3
Name and explain in your own words three of the optical artifacts of spherical mirrors. Explain why telescopes with multiple-mirrors such as Keck or the upcoming space based NGST are inferior for direct imaging of planets compared to mono-mirror systems. Why, then, are all large telescope systems are based on multiple mirror designs?
Spherical mirrors suffer from several types of optical artifacts. Coma is an effect that causes point sources to appear elongated. Astigmatism occurs when an image is focused onto slightly different points on the focal plane. Curvature of field occurs due to the fact that images are focused on a curve rather than on a plane.
Telescopes with multiple mirrors are inferior for direct imaging of planets because of the signal noise induced by the edges of the mirrors. However, most large telescopes continue to use multi-mirror designs since it is much easier to support several small mirrors rather than one large mirror.
Problem 4
Use the Rayleigh Criterion to estimate the diffraction limit (in arc sec) for the angular resolution of a typical 1m class telescope in the near IR (2 μm), and discuss the result.
The Rayleigh Criteron: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta \thickapprox 1.22 \frac{\lambda}{D} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda = 2\times10^{-6}m }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D=1m}
We plug in these values and we get that:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta \thickapprox 1.22 \frac{2\times10^{-6}m}{1m} = 2.44\times10^{-6}rad = 1.398\times10^{-4}deg = 0.503arcseconds}
Problem 5
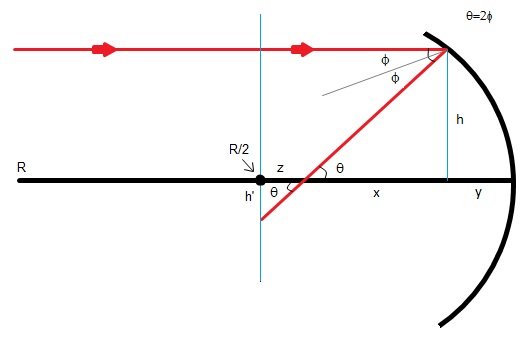
Estimate the size of the spherical aberration of a spherical mirror of 1m-diameter and a focal length of 2 meter. (Hint: Calculate the size of the smeared image of a star at the focal point and compare it to the size (in arc-sec) of an extended object, and remember your PHY2048/9).
We all know that for small angles,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=\frac{R}{2} }
Where f is the focal length and R is the radius of curvature for a spherical mirror. The problem is that with large angles, the foci will not match up, causing the aberration.
For large angles, the focal length can be written as, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'=x+y } and the angles can be determined directly through trigonometric relations from the diagram. They are,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos{\phi}=\frac{R-y}{R} } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan{\theta}=\frac{h}{x} } .
Where h is the height from the incoming light ray when the light ray strikes the mirror, to the optical axis. Solving for x and y in both of these equations, the focal length becomes,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'=\frac{h}{\tan{\theta}}+R-R\cos{\phi} }
Here I define, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta=2\phi } , so the focal length becomes,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'=\frac{h}{\tan{2\phi}}+R-R\cos{\phi} } .
Next, I define my aberration to be some variable, z. z is the horizontal distance on the optical axis between the foci. The small angle focus is at R/2 and the large angle focus occurs at the focal length f'. Therefore,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=\frac{R}{2}-f' }
Thus, plugging in our known value of f', z becomes,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=\frac{R}{2}-\frac{h}{\tan{2\phi}}-R+R\cos{\phi}. }
Using double angle formulas, and trigonometry, the angles may be parametrized out of the equation, making z only in terms of R and h. Eventually, after a little bit of tedium, z becomes,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=\sqrt{R^2+h^2}-\frac{R^2-2h^2}{2\sqrt{R^2-h^2}}-\frac{R}{2} }
This z is one of the ways to calculate the size of the spherical aberration, but it is dependent on h. Normally we know things like the focal length and the radius of curvature so I cannot directly find the numerical value of the aberration, but derivation of a similar equation based on the horizontal distance h' from R/2 to the reflected light ray being dependent on the focal length would give a value given our constants.
Also, just as check, it can easily be seen that in the limit as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h->0 } , z reduces to the expected result of zero.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=\sqrt{R^2+0}-\frac{R^2-0}{2\sqrt{R^2-0}}-\frac{R}{2} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=R-\frac{R^2}{2R}-\frac{R}{2} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=R-\frac{R}{2}-\frac{R}{2}=0 }