Solution to Set 4: Difference between revisions
Jump to navigation
Jump to search
| Line 2: | Line 2: | ||
Cu, density <math> \rho= 8.885{g\over cm^3}</math>, atomic mass <math> m_a = 63.57 amu</math>, fcc structure | Cu, density <math> \rho= 8.885{g\over cm^3}</math>, atomic mass <math> m_a = 63.57 amu</math>, fcc structure | ||
'''a.''' In <math>1 m^3</math>, the number of moles is | '''a.''' In <math>1 m^3</math>, the number of moles is | ||
<math>({8.885 g\over 1 cm^3}) ({1 cm^3\over 5\times 10^6 m^3}) ({1 mol\over 63.55 g}) = 1.40\times 10^5{mol\over m^3}</math> | <math>({8.885 g\over 1 cm^3}) ({1 cm^3\over 5\times 10^6 m^3}) ({1 mol\over 63.55 g}) = 1.40\times 10^5{mol\over m^3}</math> | ||
'''b.''' Atoms in <math>1 m^3</math> | '''b.''' Atoms in <math>1 m^3</math> | ||
<math>({1.40\times 10^5 mol\over 1 m^3}) ({6.022\times 10^{23}\over 1 mol})= 8.43\times 10^{28} atoms</math> | <math>({1.40\times 10^5 mol\over 1 m^3}) ({6.022\times 10^{23}\over 1 mol})= 8.43\times 10^{28} atoms</math> | ||
'''c.''' Since the bonds between the atoms are small compared to the diameter of the atom, we neglect the bonds for an estimate. The structure is fcc and the length of each side of the cube is <math>2r=362 pm</math>, where r is the radius of one Cu atom. | '''c.''' Since the bonds between the atoms are small compared to the diameter of the atom, we neglect the bonds for an estimate. The structure is fcc and the length of each side of the cube is <math>2r=362 pm</math>, where r is the radius of one Cu atom. | ||
'''d.''' Atomic radius | '''d.''' Atomic radius | ||
| Line 18: | Line 22: | ||
<math>r = ({3 m_a\over 4 p \pi})^{1\over 3} = 128 pm</math> | <math>r = ({3 m_a\over 4 p \pi})^{1\over 3} = 128 pm</math> | ||
'''e.''' Mass of 1 atom | '''e.''' Mass of 1 atom | ||
Revision as of 18:27, 20 February 2009
Problem 1
Cu, density , atomic mass , fcc structure
a. In , the number of moles is
b. Atoms in
c. Since the bonds between the atoms are small compared to the diameter of the atom, we neglect the bonds for an estimate. The structure is fcc and the length of each side of the cube is , where r is the radius of one Cu atom.
d. Atomic radius
, where
e. Mass of 1 atom
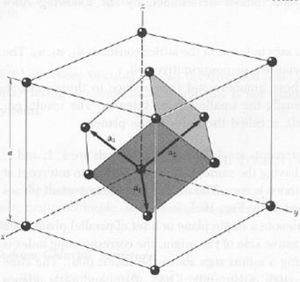
Problem 3
a. fcc and primitive cell
b.
The volume of the primitive cell is the volume of the fcc cell.
c. There are 4 atoms in the fcc cell and 6 in the primitive cell. There are 6 because there is 1 atom per vertex in the primitive cell while the fcc cell has 2 atoms per vertex and one additional atom per face.