Free electron model of metals

Classical Electron Model

Drude transport theory

The Drude theory assumes that movement of electrons can be described classically. The model resembles a pinball machine where the electrons accelerate, hit a scattering surface (positive ion), and then begin accelerating once more.

During the acceleration phase the velocity gained by the electron is described as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta v = at = -\frac{eE}{m}t}

This gives the electron a total velocity

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v = v_{0} + \Delta v\!}

Then the electron scatters off a surface. The distance between scattering surfaces is called the mean free path, $l$.

Note that on average $v_{0}$ is equal to zero since the movement is in completely random directions. So now we can calculate the average total velocity to be

$<v>\ =\ <v_{0}+\Delta v>\ =\ <v_{0}>+<\Delta v>\ =\ <\Delta v>\!$

$<\Delta v>\ \sim {\overrightarrow {E}}$

Now using the equation for current

${\overrightarrow {j}}=-ne<v>=-ne<\Delta v>\ =-{\frac {ne^{2}}{m}}<t>$

Here $<t>$ is the average time between collisions, which is called the scatter time, $\tau$.

This gives us the Drude formula ,

$\sigma =-{\frac {ne^{2}}{m}}\tau$, where $\tau ={\frac {l}{v_{0}}}$, and $\sigma$ is conductivity.

And from E&M recall that the resistivity of the material is:

$\rho ={\frac {1}{\sigma }}$

Also another often quoted value is the mobility, the proportionality constant between the velocity of the electrons and the electric field it is placed in, of the material which is:

$\mu ={\frac {e\tau }{m_{e}}}={\frac {\sigma }{ne}}$

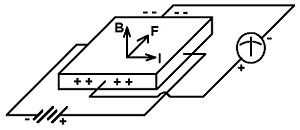
Hall effect

When a metal is placed in a magnetic field $\mathbf {B}$ and a current density $\mathbf {j}$ is passed through it, a transverse electric field $\mathbf {E_{H}}$ is set up given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{E_H} = R_H \mathbf{B} \ \times \ \mathbf{j}}

This is the Hall Effect and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_H} is known as the Hall coefficient.

This effect originates from the Lorentz Force, which makes charges pile up on opposite sides of the conductor. This creates a potential difference, or Hall Voltage, within the conductor. The internal charges will continue to pile up until it is in equilibrium with the Lorentz Force.

This set up is useful because it enables us to measure the electron mobility, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , from measured values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_H} and electronic conductivity, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} .

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = |R_H| \sigma \! }

Limitations of the classical electron model

Looking at the Drude model again and taking into account the Equipartition Theory:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}mv_{0}^{2}=k_B T}

we can show that the scattering time should be proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_0 = \sqrt{\frac{2k_B T}{m}} \sim \sqrt{T}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \tau \sim \frac{1}{\sqrt{T}}}

However, this is wrong since velocity is not proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} . When Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 0} there is still quantum uncertainty.

Pauli Principle and Fermi-Dirac statistics

Fermi Dirac Probability Distribution

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(E) = \frac{1}{e^{\frac{E-E_F}{k_B T}} +1} }