Solution to Set 3: Difference between revisions
(Infobox, Given Information, Problem #1) |
(Link to books) |
||
| Line 13: | Line 13: | ||
| Magnetic Order <br> Ferromagnetism <br> Weiss field. | | Magnetic Order <br> Ferromagnetism <br> Weiss field. | ||
|- valign="top" | |- valign="top" | ||
| '''Solid State Physics''' | | '''[[Solid State Physics]]''' | ||
| Section 8.3 <br> Section 8.4 | | Section 8.3 <br> Section 8.4 | ||
|- valign="top" | |- valign="top" | ||
| '''Soft Condensed Matter''' | | '''[[Soft Condensed Matter]]''' | ||
| Section 3.2 | | Section 3.2 | ||
|} | |} | ||
Revision as of 22:28, 8 February 2009
Ferromagnetism
| ||||||||
Given Information
- Classical Ising antiferromagnet on a ”bipartite” lattice given by Hamiltonian Failed to parse (syntax error): {\displaystyle H = \frac{J}{2} \sum_{<ij>} S_i S_j -− h\sum_i S_i } ,
- Magnetization for Lattice A:
- Magnetization for Lattice B:
- Average magnetization:
- "Staggered” magnetization:
(Note: It's the difference between the two sublattices)
- for perfect ferromagnetic order
- for perfect antiferromagnetic order
Part 1
Use Weiss mean-field decoupling to replace one of the spins in the Hamiltonian by its thermal average. The Weiss field experienced by a given spin is then proportional to the sublattice magnetization on the other sublattice. Write down self-consistent equations for and , and express them through the order parameters and .
The Weiss Molecular Field
Chapter 8.3.1 of Solid State Physics The systematic way of replacing the spin operator in the Heisenberg Hamiltonian by their average values in order to obtain the Weiss molecular field approximation is to insert and into Failed to parse (syntax error): {\displaystyle H = \frac{J}{2} \sum_{<ij>} S_i S_j -− h\sum_i S_i }
Part 2
Assume that , so that , and solve the mean-field equations by expanding in . Determine the Neel (ordering) temperature, and calculate the order-parameter exponent.
The Néel Temperature
Chapter 8.4 of Solid State Physics
where
- is Néel Temperature, the onset temperature for antiferromagnetism
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C = \frac {N \mu_0 g^2 \mu_b^2}{k_B}} is Curie constant
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda = \frac{4 \sum_{j \neq i} \jmath_{i j}} {N \mu_0 g^2 \mu_b^2} = - \frac{4 z \jmath} {N \mu_0 g^2 \mu_b^2}}
Part 3
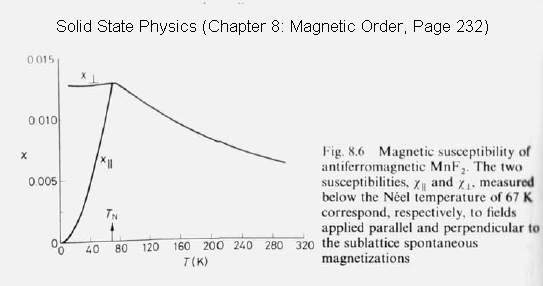
Now consider a small external field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h > 0\;} , so that both order parameters can assume a nonzero value (Note: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\;} will be small). By keeping only the leading terms in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h\;} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\;} , calculate the uniform spin susceptibility Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi = \partial m/ \partial h} , as a function of temperature. Plot Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi\;} as a function of temperature, and show that it has a cusp around Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_N\;} .
Part 4
Imagine adding a ”staggered” external field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h^{\dagger}} , which would be positive on sublattice A, but would be negative on sublattice B. Concentrate on the system with no uniform field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (h = 0)\;} , and determine the behavior of the staggered susceptibility Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi^{\dagger}= \partial m^{\dagger} / \partial h^{\dagger} } . Show that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi^{\dagger}} blows up at the Neel temperature.