Solution to Set 4: Difference between revisions
Jump to navigation
Jump to search
| Line 26: | Line 26: | ||
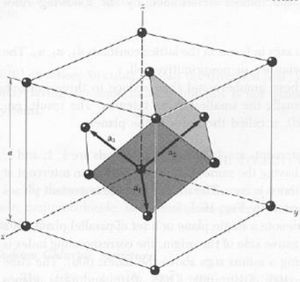
'''a.''' fcc and primitive cell | '''a.''' fcc and primitive cell | ||
[[Image:fcc.JPEG|thumb|center|300px|]] | |||
'''b.''' <math>V_fcc = lwh = a_1 a_2 a_3 = {1\over 2}a(x+y) {1\over 2}a(y+z) {1\over 2}a(z+x) = {1\over 8}a^3({1\over 2} + {1\over 2}) (1+1) ({1\over 2} + {1\over 2}) = {1\over 4}a^3</math> | '''b.''' <math>V_fcc = lwh = a_1 a_2 a_3 = {1\over 2}a(x+y) {1\over 2}a(y+z) {1\over 2}a(z+x) = {1\over 8}a^3({1\over 2} + {1\over 2}) (1+1) ({1\over 2} + {1\over 2}) = {1\over 4}a^3</math> | ||
| Line 31: | Line 33: | ||
The volume of the primitive cell is <math>{1\over 4}</math> the volume of the fcc cell. | The volume of the primitive cell is <math>{1\over 4}</math> the volume of the fcc cell. | ||
'''c.'''There are 4 atoms in the fcc cell and 6 in the primitive cell. There are 6 because there is 1 atom per vertex in the primitive cell while the fcc cell has 2 atoms per vertex and one additional atom per face. | '''c.''' There are 4 atoms in the fcc cell and 6 in the primitive cell. There are 6 because there is 1 atom per vertex in the primitive cell while the fcc cell has 2 atoms per vertex and one additional atom per face. | ||
Revision as of 18:25, 20 February 2009
Problem 1
Cu, density , atomic mass , fcc structure
a. In , the number of moles is
b. Atoms in
c. Since the bonds between the atoms are small compared to the diameter of the atom, we neglect the bonds for an estimate. The structure is fcc and the length of each side of the cube is , where r is the radius of one Cu atom.
d. Atomic radius
, where
e. Mass of 1 atom
Problem 3
a. fcc and primitive cell
b.
The volume of the primitive cell is the volume of the fcc cell.
c. There are 4 atoms in the fcc cell and 6 in the primitive cell. There are 6 because there is 1 atom per vertex in the primitive cell while the fcc cell has 2 atoms per vertex and one additional atom per face.