Homeworks 4: Difference between revisions
(→Problem 1: Rearranging pictures) |
|||
| Line 3: | Line 3: | ||
==Problem 1== | ==Problem 1== | ||
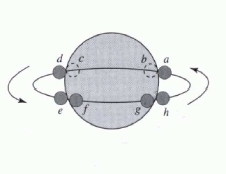
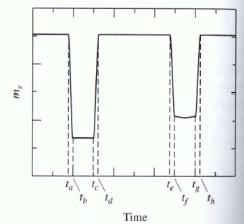
A spectroscopic, eclipsing binary system has an orbital period of 6 years, and the maximum radial velocities are 5 and 22 km/sec, respectively. The period between first contact and minimum light (<math>t_b</math> − <math>t_a</math>) is 0.6 days, and the length of the primary minimum (<math>t_c</math> − <math>t_a</math>) 0.6 days. The apparent bolometric magnitudes at maximum, primary and secondary minimum at 5.40, 9.2 | A spectroscopic, eclipsing binary system has an orbital period of 6 years, and the maximum radial velocities are 5 and 22 km/sec, respectively. The period between first contact and minimum light (<math>t_b</math> − <math>t_a</math>) is 0.6 days, and the length of the primary minimum (<math>t_c</math> − <math>t_a</math>) is 0.6 days. The apparent bolometric magnitudes at maximum, primary and secondary minimum at 5.40, 9.2 and 5.44 magnitudes, respectively. a) Describe in your own words, how you can derive the observables from the LCs given below. Assuming spherical orbits, determine b) the total mass of the system, c) the individual masses, d) the individual radii, and e) the ratio of effective temperatures. | ||
[[Image:Orbit.jpg]] [[Image:M vs T.jpg]] | [[Image:Orbit.jpg]] [[Image:M vs T.jpg]] | ||
Revision as of 19:12, 25 September 2009
Homework 4 due on 09/28/2009
Problem 1
A spectroscopic, eclipsing binary system has an orbital period of 6 years, and the maximum radial velocities are 5 and 22 km/sec, respectively. The period between first contact and minimum light ( − ) is 0.6 days, and the length of the primary minimum ( − ) is 0.6 days. The apparent bolometric magnitudes at maximum, primary and secondary minimum at 5.40, 9.2 and 5.44 magnitudes, respectively. a) Describe in your own words, how you can derive the observables from the LCs given below. Assuming spherical orbits, determine b) the total mass of the system, c) the individual masses, d) the individual radii, and e) the ratio of effective temperatures.
Problem 2
Sketch the H-R diagram indicating the location of main sequence stars, red giants, and white dwarfs. Label the axes with the correct temperatures and luminosities.
Problem 3
Two stars, A and B, have the same temperature, but their luminosities are 9.0 and 0.25 times the luminosity of the sun respectively. What is the ratio of the surface areas of the two stars? What is the ratio of their radii?
Problem 4
What are the luminosities and radii of the following stars in solar luminosities () and solar radii ()? a) Vega, a main-sequence star with a temperature of 10,000 K. b) Barnard’s star, a main sequence star with a temperature of 3000 K. c) Sirius B, the white dwarf companion to Sirius with a temperature of 10,000 K. d) Betelgeuse, a supergiant star with a temperature of 3000 K. e)Aledebaran, a red giant with a temperature of about 4500 K.
Problem 5
In first order, stellar spectra can be described by a black body (Planck function) of a certain temperature T based on the flux distribution in the optical wavelength range. Derive an expression for the frequency integrated flux as a function of T (show the steps), and provide an expression for the total luminosity of a star with Radius R. Estimate the total luminosity of the sun assuming a radius R of 6.96E10 cm and, based on its color, a temperature of 5400 K. Compare the result with the bolometric luminosity from literature.