Phy5645/Double pinhole experiment

Submitted by team 1

---

(a) As directed, we assume that the denominators are approximately the same between two waves. This is justified because the corrections are only of the order of $d/l\!$, and we are interested in the case where $d<<L\!$. We require that the numerators have the same phase, namely $kr_{+}-kr_{-}=2\pi n\!$. We expand the LHS with respect to $d\!$,

${\begin{aligned}k(r_{+}-r_{-})&\approx k\left\{\left({\sqrt {L^{2}+x^{2}+y^{2}}}+{\frac {yd}{2{\sqrt {L^{2}+x^{2}+y^{2}}}}}\right)\right.\\&-\left.\left({\sqrt {L^{2}+x^{2}+y^{2}}}-{\frac {yd}{2{\sqrt {L^{2}+x^{2}+y^{2}}}}}\right)\right\}\\&=k{\frac {dy}{\sqrt {L^{2}+x^{2}+y^{2}}}}\end{aligned}}$

Therefore,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\frac{dy}{\sqrt{L^{2}+x^{2}+y^{2}}}=2\pi n\!}

and hence

${\frac {y}{\sqrt {L^{2}+x^{2}+y^{2}}}}=n{\frac {\lambda }{d}}\!$

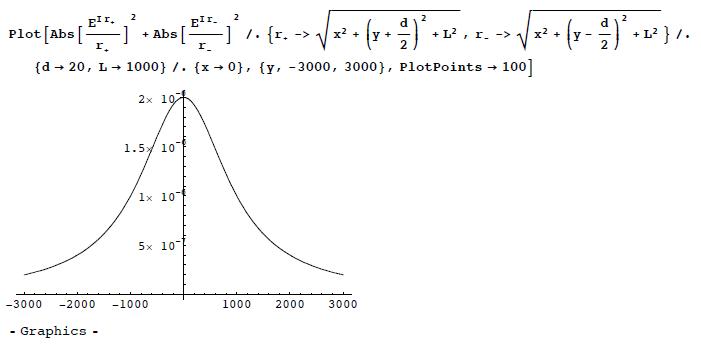
(b) Let us choose the unit where k = 1. Then we pick d = 20, L = 1000. Here is the interference pattern. First along the y-axis (x = 0):

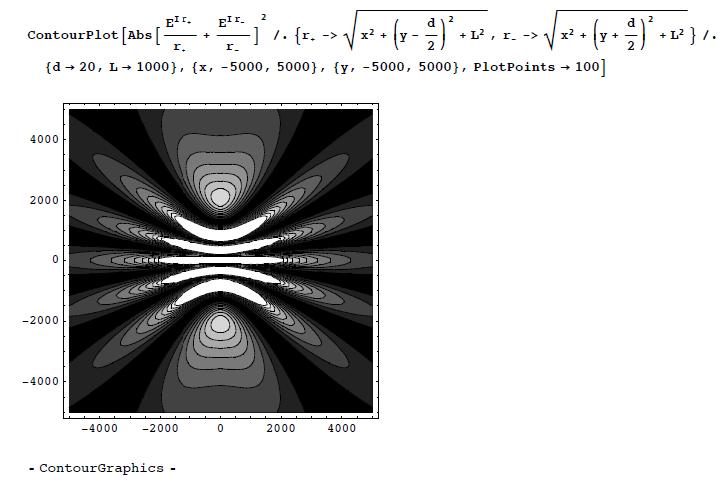
(c) Now on the plane:

(d) For the same parameter as in (b), First along the y-axis (x = 0):

Now on the plane:

The main difference is the absence of the interference pattern.

Back to Stern-Gerlach Experiment